Nr ćwiczenia |
LABORATORIUM AUTOMATYKI |
Wykonanie |
1 |
|
Bartłomiej Ignaczak, Michał Adamczyk Filip Chodań, Krzysztof Dominkiewicz |
Rok i grupa |
Data wykonania i oddania |
Ocena |
III Tm Ab |
wyk 18 09 2000 oddane 25 09 2000 |
|
Układy regulacji z regulatorami dwupołożeniowymi
(regulacja dwustawna)
Wprowadzenie
Do grupy regulatorów przekaźnikowych zalicza się regulatory dwupołożeniowe i trój położeniowe krokowe oraz impulsowe. Wspólną cechą tych regulatorów jest nieciągłość sygnału wyjściowego x, który przyjmować może tylko dwie lub trzy wartości, zależnie od rodzaju elementu przekaźnikowego stanowiącego podstawową część funkcjonalną regulatora.
Układy regulacji z regulatorami przekaźnikowymi są nieliniowe jednak w niektórych przypadkach, dzięki objęciu elementu przekaźnikowego sprzężeniem zwrotnym lub dołączeniu do regulatora członu wykonawczego o działaniu całkującym, można również analizować przybliżone własności układu metodami liniowymi.
Zakres zastosowań regulatorów przekaźnikowych jest dość szeroki. Zwłaszcza regulatory dwu- i trój położeniowe, ze względu na prostą budowę i niską cenę, chętnie stosowane są np. w układach regulacji elektrycznych urządzeń grzejnych, gdzie rola ich sprowadza się do załączania lub wyłączania obwodu grzejnego w zależności od temperatury obiektu.
Istotne jest również poznanie własności układów impulsowych, których rozpowszechnienie wiąże się z coraz szerszym zakresem automatyzacji kompleksowej. Użycie komputerów, które mogą kolejno sterować wieloma układami regulacji, powoduje, że każdy z tych układów rozpatrywany oddzielnie staje się układem regulacji impulsowej.
W układach regulacji dwupołożeniowej zadania regulatora, spełnia przekaźnik dwupołożeniowy, którego charakterystyki przedstawiono na rys. "W najbardziej typowym przypadku zastosowania do regulacji temperatury,
yo yo
Rys. Charakterystyki statyczne regulatorów dwupołożeniowych: idealnego i z histerezą 1 — zestyk zamknięty, 2 — zestyk otwarty
działanie regulatora idealnego można opisać, jak następuje: jeżeli temperatura obiektu jest mniejsza od zadanej, y< y o, to regulator załącza obwód grzejny, a jeżeli zachodzi y > yo -wyłącza. Zastosowanie regulatorów dwu położeniowych może być też uzasadnione w innych przypadkach, gdy obiekty regulacji mają własności elementów inercyjnych lub całkujących o dużej stałej czasowej, a urządzenie wykonawcze ma działanie dwustanowe.
Regulatory PID
Regulatorem PID nazywamy korektor proporcjonalno całkująco różniczkujący jego równanie różniczkowe przedstawia się
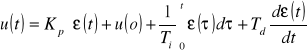
gdzie kp to współczynnik wzmocnienia proporcjonalnego regulatora
Ti stała całkowania
Td stała różniczkowania
a jego transmitancja czyli stosunek transformaty la'Placea odpowiedzi członu do transformaty la'Placea wymuszenia równa się:
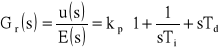
Regulator PID zapewnia połączenie zalet wszystkich elementów P, D, I. Zapewnia astatyzm przy rozszerzonym paśmie regulacji z zachowaniem zapasu stabilności. Jego charakterystyki przedstawiam poniżej.
korektor PID
obiekt
korektor + obiekt
Przebieg ćwiczenia
Ćwiczenie wykonujemy na komputerowych symulatorach układów rzeczywistych co pozwala na sprawdzenie działania układów regulacji w szybki sposób. Pozwala także na łatwy dobór parametrów oraz natychmiastową obserwacje efektów działania regulatorów. Testujemy dwa układy PID oraz jeden PD. Ponieważ nie zależy nam na powtarzalności wyników ani na bardzo dokładnych wyliczeniach możemy dobierać parametry w sposób bardziej dowolny a także zmieniać je co pozwoli zapoznać się z charakterystykami regulatorów.
regulacja dwustawna regulator PD
schemat układu
celem naszym było określenie skuteczności działania regulatora dwustawnego. Po wprowadzeniu parametrów yo=3 i x=0.5 otrzymujemy następujący wykres.
przykład ten pokazuje w jaki sposób można stosować regulację dwustawna w prostych układach automatyki. Pola zakreskowane odpowiadają stanowi wyłączony a przerwy między nimi załączony. Ponieważ układy idealne nie istnieją zawsze musimy brać pod uwagę wpływ histerezy i odpowiednio go kompensować.
Regulacja Dwustawna Regulator PID
identyfikacja obiektu
W przypadku regulacji PID należy najpierw zapoznać się z charakterystyka obiektu co pozwoli zakwalifikować obiekt (może się bowiem okazać że nie nadaje się do zastosowania z regulatorem PID) oraz dobrać parametry pracy regulatora. W tym celu wyznaczmy styczna do charakterystyki i odczytujemy wykresu interesujące nas dane.
obliczanie wartości charakterystycznych
Odczytujemy To=0.4 T=6
Podstawiamy do wzorów
kp = ![]()
![]()
Ti = T 1.7T
Td= ![]()
![]()
Pierwsze wzory dotyczą optymalnego modulatora a drugie do stabilizatora aperiodycznego. Obydwa zastosowania oddają w sposób właściwy charakterystyki regulatorów PID
kp - wzmocnienie proporcjonalne
Ti - czas zdwojenia (stała czasowa akcji całkującej)
Td - czas wyprzedzenia (stała czasowa akcji różniczkującej)
zamiast kp możemy podać zakres proporcjonalności Xp
charakterystykę skokową (rzeczywisty PID) zatem można by przedstawić
Transmitancja zatem wynosi
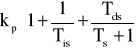
a równanie charakterystyki skokowej
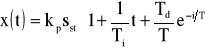
Mając na względzie powyższe założenia i używając otrzymane wartości możemy przystąpić do testów układu
kp=0.08
Td=0.13
Ti=0.4
Poniżej przedstawiam wykres jaki możemy obserwować na ekranie(zobrazowuje prace regulatora)
Ta>Tb i Ta>4Tb
Ponieważ jak już zaznaczyłem i powtórzę jeszcze raz nie chodzi nam o dokładne odzwierciedlenie charakterystyk ale o zrozumienie problemu, oraz wpływ zmiany wzmocnienia i innych parametrów na pracę układu
W założeniu jest to obiekt inercyjny (należy dodać pierwszego rzędu), regulator zaś ma charakterystykę przekaźnikową (rzeczywistą czyli z histerezą) zatem krzywa charakteryzująca pracę układu swym przebiegiem przypomina piłę. Widzimy tutaj regularne oscylacje wartości regulowane wokół wartości zadanej Jest to przykład dobrze wyregulowanego sterownika
Następnie możemy wykonać kilka prób zmiany nastaw. Zmieniając wzmocnienie doprowadzamy do sytuacji w której stabilizator nie wyłącza się. Przedstawiam to na wykresie poniżej
Następnie możemy nieznacznie pomanipulować wartością Ti
Możemy mówić o małym zapasie stabilności a zwiększając Ti powiększamy go, do momentu przekroczenia progu po którym stabilizator przestaje spełniać swą funkcję . Należy przy tym także zwrócić uwagę na zwiększanie wzmocnienia (charakterystyka amplitudowa przesuwa się do góry przy nie zmienionym położeniu charakterystyki fazowej) wpływa to bardzo niekorzystnie na stabilność układu. Jak widać z charakterystyki regulator działa ale nie może być mowy o stabilności.
Należy jeszcze wyjaśnić dlaczego mówimy o regulatorach quasi PID i quasi PD. Pojęcia te biorą się z stąd iż w przyrodzie nie występują obiekty idealne. Nie można zatem zbudować idealnego regulatora (co by i tak nie miało sensu. Aby zrozumieć sens działania regulatorów z przedrostkiem quasi należy się posłużyć równaniem przebiegów regulatora i obiektu. Po przekształceniach dochodzimy do równania częstotliwości dla regulatorów PID i PD możemy dojść do wniosku że niemożliwe jest regulowanie parametrów kp i Td w sposób dowolny, możemy za to wpływać na szerokość pętli histerezy
1
2
1
2
OBIEKT STEROWANIA
REGULATOR
yo
e
x
+
-
0,5
ω
-2
-1
0
1/Ti
1/Td
1/Tα
-π
-π/2
ω
T
To
t
k
Ti
x(t)
t
![]()
kpest
est
e(t)
yo
T
Ta
Tb
yo
yo
Wyszukiwarka
Podobne podstrony:
Sprlo4, Szkoła, penek, Przedmioty, Nawigacja, Zaliczenia, egzaminy, CAIMER
W rozwiązywanych przykł przy zmi a na aa i odwrotni, Szkoła, penek, Przedmioty, Nawigacja, Zaliczeni
Dzieciol, Szkoła, penek, Przedmioty, Nawigacja, Zaliczenia, egzaminy, CAIMER
lozowicka egazm, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
4x test A4, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
ZESTAW III IV1, Szkoła, penek, Przedmioty, Chemia, Zaliczenia, egzaminy, Przykłady zaliczenia z che
Kwit na fize, Szkoła, penek, Przedmioty, Fizyka, Zaliczenie, egzamin
zaliczenie2, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
Budowa i Stateczność, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
sesja fizyka ITM, Szkoła, penek, Przedmioty, Fizyka, Zaliczenie, egzamin
4x test ściąga kolumny, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
Powiększona ściąga, Szkoła, penek, Przedmioty, BISS, Zaliczenia, egzaminy
ZESTAW III IV, Szkoła, penek, Przedmioty, Chemia, Zaliczenia, egzaminy, Przykłady zaliczenia z chem
więcej podobnych podstron