Ciąg dalszy:

Zatem jeśli eliminację Gaussa można wykonać do końca, to układ
można zapisać:

Etap I - jest równoważny przekształceniu wyjściowego układu do postaci
.

Wyznaczenie x polega na rozwiązaniu dwóch układów z macierzami trójkątnymi.

gdzie
(obliczanie
)

Ilość obliczeń gdy znamy rozkład LU:

mnożeń i dzieleń

dodawań

tyle samo, co przy obliczaniu

gdy znane

Korzyść z rozkładu LU

Rozwiązywanie wielu układów o tej samej max A i różnych prawych stronach (zwłaszcza zależnych od x).

Przechowywanie w pamięci

Zauważmy:
dla
można wpisać w miejsce
zaraz po obliczeniu;

Elementów
nie trzeba pamiętać
i U w miejsce A;

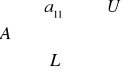
Twierdzenie (o rozkładzie trójkątnym)

Niech -->
,
[Author:JDz] utworzone z elementów początkowych k - wierszy i kolumn A.

Jeśli
(
) to istnieje jedyny rozkład
na czynniki takie, że L jest macierzą trójkątną dolną oraz
, a macierz U jest trójkątna górna.

Przykład macierzy A, która nie ma rozkładu LU

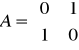
(nieosobliwa)

METODY ITERACYJNE

załóżmy

jeśli nie, to przestawiamy wiersze A

można zapisać

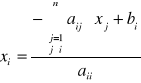
(1)

Metoda Jakobiego (iteracji prostej)

Tworzy się ciąg przybliżeń

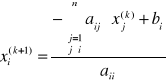
(2)

jako początkowe przybliżenie często przyjmuje się

jeśli
to x jest rozwiązaniem pierwotnego układu.

Metoda Gaussa-Seidela

Używa bezpośrednio ulepszonych wartości do obliczenia pozostałych zmiennych, w tej samej iteracji:

-->
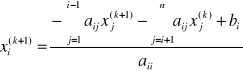
[Author:JDz] (3)

Jednocześnie trzeba pamiętać tylko jedno --> przybliżenie[Author:JDz] .

Zbieżność szybsza niż w metodzie Jakobiego, lecz metoda może być użyta tam, gdzie Jakobiego jest zbieżna.

ZBIEŻNOŚĆ

Powyższe metody można wyrazić w postaci

(4)

opisującej ogólnie metody iteracyjne stacjonarne

gdyż:

-->


(5)
[Author:JDz]

naddiagonalna

poddiagonalna

metoda Jakobiego

(6)

metoda Gaussa-Seidela

(7)

(6), (7) są szczególnymi postaciami (4)

gdzie

Twierdzenie:

Warunkiem koniecznym i wystarczającym, aby metoda stacjonarna
była zbieżna dla dowolnego przybliżenia początkowego
jest nierówność:

gdzie
jest promieniem spektralnym macierzy B

APROKSYMACJA (czyli przybliżanie funkcji)

rysunki

- znana lub określona tablicą

- funkcja aproksymująca

Przybliżenie obarczone błędem aproksymacji.

Aproksymacja liniowa.

X - przestrzeń liniowa unormowana (skończenie lub nieskończenie wymiarowa)

(funkcja aproksymowana)

- n - wymiarowa podprzestrzeń liniowa przestrzeni X

Aproksymacja funkcji
polega na wyznaczeniu takich współczynników
funkcji
(1), gdzie
są funkcjami bazowymi
- wymiarowej podprzestrzeni liniowej
, aby
spełniała pewne warunki, np. optymalizowała normę różnicy
.

Są też inne typy aproksymacji, np. aproksymacja wymierna określona:

gdzie
,
są elementami tej samej bazy k - wymiarowej podprzestrzeni liniowej
, zaś
,
są stałymi współczynnikami, które należy wyznaczyć.

Aproksymacja Pade'go

Zastosowania - rozwiązywanie zagadnień chemii i fizyki

Aproksymacja liniowa

Trzeba określić:

• odpowiednią podprzestrzeń liniową
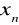
  i związaną z nią bazę

• odpowiednią normę

Wybór podprzestrzeni

Jeśli funkcja
jest ciągła na przedziale

to funkcje
będą elementami pewnej
- wymiarowej podprzestrzeni
- jakiej?

1. Jeśli
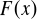
   jest okresowa, to przydatna jest podprzestrzeń funkcji trygonometrycznych z bazą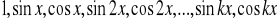
   .

2. Podprzestrzeń wielomianów stopnia co najwyżej n z bazą jednomianów
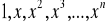
   lub z bazą wielomianów Czebyszewa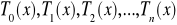
   

funkcje bazowe mało wrażliwe na błędy

lub bazę wielomianów Lagrange'a

Czyli chodzi o to, żeby wszystkie minory główne były różne od zera

Jaki podział w indeksach sumy? Aha! Uzywamy nowo obliczonych wartości k+1 kroku dla x-ów o mniejszych indeksach niż aktualny

Że niby które?

What the fuck!?

---