POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI PRZEMYSŁOWEJ Zakład Podstaw Elektrotechniki
LABOLATORIUM ELEKTROTECHNIKI TEORETYCZNEJ Ćwiczenie nr 6  Temat: Rezonans w obwodzie szeregowym.
Rok akad: 2007/08 Wydział elektryczny Studia dzienne magisterskie Grupa E2/2	1. Dawid Jacaszek 2. Norbert Bronisz 3. Krzysztof Dobiegała 4. Arkadiusz Chełczyński 5. Kamil Brodziński	Data
				Wykonania ćwiczenia	Oddania sprawozdania
				03.04.2008	10.04.2008
				Ocena:
Uwagi:

1. Wstęp teoretyczny:

Rezonansem napięć nazywamy taki stan obwodu szeregowego RLC, w którym impedancja obwodu ma charakter wyłącznie czynny. Zachodzi to wówczas, gdy: X_L=X_C. Równość obu reaktancji może być osiągnięta bądź drogą zmiany wartości elementów L, C, bądź też drogą zmiany częstotliwości źródła zasilającego. Nastąpi to dla tzw. „pulsacji rezonansowej”: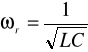
.

Dla częstotliwości rezonansowej mamy:

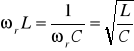
Jest to impedancja falowa lub charakterystyczna dwójnika:

Wartość skuteczna prądu w obwodzie RLC zasilanym napięciem o wartości skutecznej U wynosi:

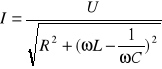
Dla częstotliwości rezonansowej dzielimy napięcie tylko przez rezystancję:

Dzieląc równania otrzymujemy:

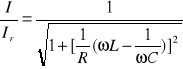
Rozstrojenie bezwzględne wyraża się wzorem:

Przekształcając je otrzymujemy następującą postać:

Gdzie wielkość
jest rozstrojeniem względnym, a
jest dobrocią cewki.

Ogólnie dobroć zapisujemy jako stosunek napięcia na kondensatorze lub cewce do napięcia na rezystancji:

Zatem rozstrojenie bezwzględne można zapisać jako:

Szerokością pasma przepuszczania obwodu rezonansowego nazywa się przedział częstotliwości w otoczeniu częstotliwości rezonansowej, na którego końcach wartość skuteczna prądu zmniejsza się o

3 dB, czyli:

Podstawiając tą własność do funkcji
otrzymujemy, że
czyli
.Wiedząc że
i dokonując przekształceń, otrzymujemy wzór na szerokość pasma przepuszczania:

Maksymalne napięcia na cewce i kondensatorze podczas rezonansu SA sobie równe i wynoszą:

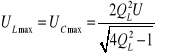
1. Przebieg ćwiczenia:

2.1. Wyznaczenie charakterystyki spadku napięcia na rezystancji (prądu) w funkcji częstotliwości

2.1.1. Schemat połączeń

 

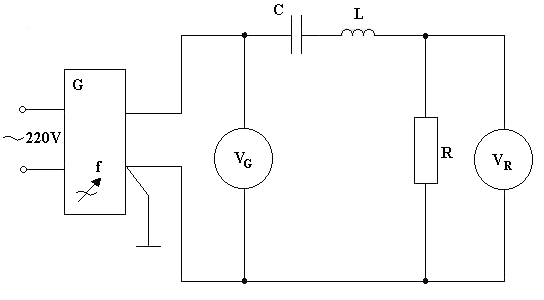
Dane:U=0.8 [V], R=1000 [W], L=56 [mH], C=5060 [pF]

 

2.1.2. Przebieg pomiarów

 

Po połączeniu układu według schematu z punktu 2.1.1. tak sterowaliśmy napięciem z generatora aby jego wartość wynosiła 0,8
0,02 [V]. Wykonaliśmy pomiary napięcia na rezystancji dla zadanych częstotliwości. Poszukaliśmy taką częstotliwość generatora, aby wystąpił maksymalny spadek napięcia na rezystancji. Częstotliwość ta wyniosła 9.5 kHz. Wyniki pomiarów zamieściłem w tabeli poniżej.

2.1.3. Wyniki pomiarów i obliczeń: 

Lp		ω/ω0		I/I0
1		0,421		0,150
2		0,526		0,213
3		0,632		0,300
4		0,737		0,438
5		0,874		0,738
6		0,905		0,825
7		0,937		0,900
8		0,968		0,963
9		1,000		0,975
10		1,032		0,963
11		1,063		0,913
12		1,095		0,850
13		1,126		0,775
14		1,158		0,713
15		1,263		0,538
16		1,368		0,413
17		1,474		0,338
18		1,579		0,288
19		1,684		0,250
20		1,789		0,213
Lp.		f		UR
				[kHz]		[V]
1		4		0,12
2		5		0,17
3		6		0,24
4		7		0,35
5		8,3		0,59
6		8,6		0,66
7		8,9		0,72
8		9,2		0,77
9		9,5		0,78
10		9,8		0,77
11		10,1		0,73
12		10,4		0,68
13		10,7		0,62
14		11		0,57
15		12		0,43
16		13		0,33
17		14		0,27
18		15		0,23
19		16		0,2
20		17		0,17

Przykładowe obliczenia: Dla punktu pierwszego mamy:

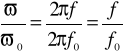
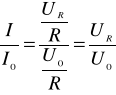
Charakterystyka zależności wartości skutecznej napięcia na rezystancji w funkcji częstotliwości U_R=f(f).

Charakterystyka: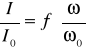
:

2.2. Wyznaczenie charakterystyki napięcia na cewce w funkcji częstotliwości

2.2.1. Schemat połączeń

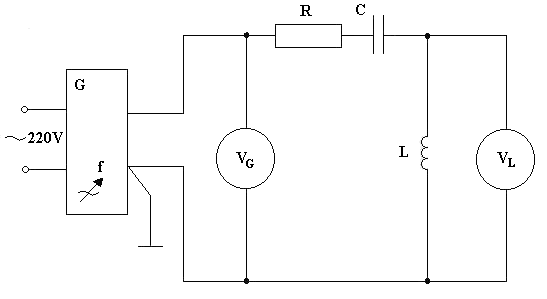
Dane: U=0.8 [V], R=1000 [W], L=56 [mH], C=5060 [pF]

 2.2.2. Przebieg pomiarów

 

Po dokonaniu połączeń według powyższego schematu zmieniając wartości częstotliwości poszukaliśmy taką jej wartość, przy której wstąpił maksymalny spadek napięcia na cewce. Następnie dokonaliśmy pomiarów napięcia na cewce przy różnych częstotliwościach, utrzymując stałą wartość napięcia generatora U_G =2,00
0,02 [V]. Wyniki pomiarów zamieściłem w tabeli poniżej.

2.2.3. Wyniki pomiarów i obliczeń:

Lp.	f		UL
		[kHz]		[V]
1	4		0,17
2	5		0,3
3	6		0,51
4	7		0,87
5	8,5		1,9
6	8,8		2,18
7	9,1		2,42
8	9,4		2,57
9	9,7		2,63
10	10		2,6
11	10,3		2,49
12	10,6		2,35
13	10,9		2,22
14	11,2		2,08
15	12		1,8
16	13		1,56
17	14		1,39
18	15		1,28
19	16		1,21
20	17		1,15
Lp.		ω/ω0		UL/U0
1		0,412		0,213
2		0,515		0,375
3		0,619		0,638
4		0,722		1,088
5		0,876		2,375
6		0,907		2,725
7		0,938		3,025
8		0,969		3,213
9		1,000		3,288
10		1,031		3,250
11		1,062		3,113
12		1,093		2,938
13		1,124		2,775
14		1,155		2,600
15		1,237		2,250
16		1,340		1,950
17		1,443		1,738
18		1,546		1,600
19		1,649		1,513
20		1,753		1,438

Przykładowe obliczenia dla punktu pierwszego:

Charakterystyka zależności wartości skutecznej napięcia na cewce w funkcji częstotliwości U_L=f(f).

Charakterystyka: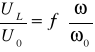
:

 

2.3. Wyznaczenie charakterystyki napięcia na kondensatorze w funkcji częstotliwości

 

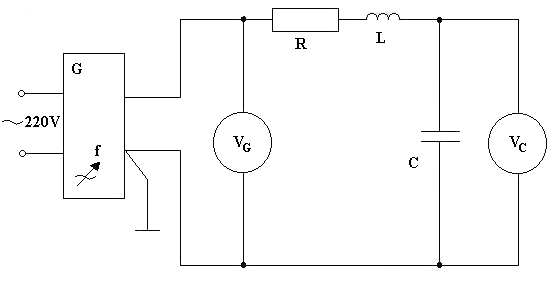
2.3.1. Schemat połączeń

Dane: U=0.8 [V], R=1000 [W], L=56 [mH], C=5060 [pF]

 

2.3.2. Przebieg pomiarów

 

Po połączeniu układu zgodnie z powyższym schematem podobnie jak dla poprzednich układów regulując częstotliwość generatora, szukaliśmy takiej jej wartości, przy której występował maksymalny spadek napięcia na kondensatorze. Następnie dokonaliśmy pomiarów napięcia na kondensatorze dla różnych wartości częstotliwości, utrzymując stałą wartość napięcia generatora U_G = 2,00
0,02 [V] . Wyniki pomiarów zamieściłem w tabeli poniżej.

2.3.3. Wyniki pomiarów i obliczeń:

  

Lp.	f	UC
		[kHz]	[V]
1	4	0,97
2	5	1,1
3	6	1,3
4	7	1,61
5	8	2,09
6	8,3	2,27
7	8,6	2,45
8	8,9	2,56
9	9,2	2,63
10	9,5	2,58
11	9,8	2,44
12	10,1	2,24
13	10,4	2,02
14	10,7	1,8
15	11	1,61
16	12	1,11
17	13	0,82
18	14	0,62
19	15	0,5
20	16	0,41
Lp.	ω/ω0		UC/U 0
1	0,435		1,213
2	0,543		1,375
3	0,652		1,625
4	0,761		2,013
5	0,870		2,613
6	0,902		2,838
7	0,935		3,063
8	0,967		3,200
9	1,000		3,288
10	1,033		3,225
11	1,065		3,050
12	1,098		2,800
13	1,130		2,525
14	1,163		2,250
15	1,196		2,013
16	1,304		1,388
17	1,413		1,025
18	1,522		0,775
19	1,630		0,625
20	1,739		0,513

Przykładowe obliczenia dla punktu pierwszego:

Charakterystyka zależności wartości skutecznej napięcia na kondensatorze w funkcji częstotliwości U_C=f(f).

Charakterystyka:
:

3. Obliczenia:

 

3.1. Obliczenia wykonane na podstawie danych parametrów:

 a) pulsacja rezonansowa:

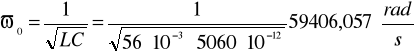
b) częstotliwość rezonansowa:

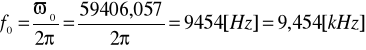
c) dobroć obwodu:

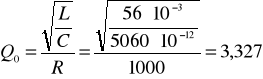
d) dobroć cewki i kondensatora przy pulsacji rezonansowej:

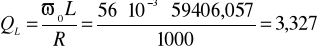
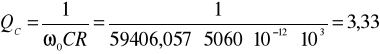
3.2. Charakterystyki U_R, U_L, U_C w funkcji częstotliwości dla układu szeregowego (na jednym wykresie):

3.3. Wyznaczanie dobroci obwodu rezonansowego Q₀ z charakterystyki przebiegu napięcia na rezystancji U_R=f(f):

Częstotliwości f₁ i f₂ odczytane z wykresu wynoszą:

f₁=8,1 kHz

f₂=11,1 kHz

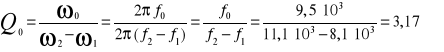
3.4. Wyznaczanie dobroci obwodu rezonansowego z charakterystyk przebiegu napięć na cewce i kondensatorze (U_L,U_C=f(f)):

Z charakterystyki  U_R=f(f) U_L=f(f) U_C=f(f) odczytałem wartość napięcia na rezystorze dla

częstotliwości rezonansowej f₀:

Obliczam dobroć obwodu rezonansowego: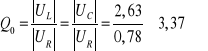
.

3.5. Tabela obliczeń i charakterystyki: R, X_L, X_C, Z, X_L -X_C=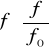
.

Lp.	R	XL	XC	XL- XC	Z
1	1000	0,056	5,06E-09	-6460,655	6537,59
2	1000	0,056	5,06E-09	-4535,500	4644,43
3	1000	0,056	5,06E-09	-3134,837	3290,47
4	1000	0,056	5,06E-09	-2033,883	2266,42
5	1000	0,056	5,06E-09	-944,407	1375,47
6	1000	0,056	5,06E-09	-696,722	1218,78
7	1000	0,056	5,06E-09	-458,956	1100,29
8	1000	0,056	5,06E-09	-230,107	1026,13
9	1000	0,056	5,06E-09	-9,302	1000,04
10	1000	0,056	5,06E-09	204,221	1020,64
11	1000	0,056	5,06E-09	411,131	1081,22
12	1000	0,056	5,06E-09	612,016	1172,42
13	1000	0,056	5,06E-09	807,399	1285,26
14	1000	0,056	5,06E-09	997,741	1412,62
15	1000	0,056	5,06E-09	1359,296	1687,51
16	1000	0,056	5,06E-09	1949,382	2190,91
17	1000	0,056	5,06E-09	2502,789	2695,17
18	1000	0,056	5,06E-09	3027,379	3188,26
19	1000	0,056	5,06E-09	3528,913	3667,864
20	1000	0,056	5,06E-09	4011,716	4134,473

Przykładowe obliczenia dla punktu pierwszego:

R = 1000

X_L = ω * L = 2*3,14*4*10³*0,056 = 1406,72

X_C = 1/ω*C = 1/(2*3,14*4*10³*5060 * 10^-12 = 7867,375

X_L- X_C = 1406,72 - 7867,375 = -6460,655

Z = (R²+X²)^0,5 = (1000²+6460,665²)^0,5 = 6537,59

4. Parametry i dane zmianowe zastosowanych urządzeń i mierników.

Generator funkcyjny GFG-3015.

Płytka do badania rezonansu szeregowego.

Dwa mierniki uniwersalne BRYMEN BM 857 

Wnioski:

Myślę, że wyniki, jakie uzyskaliśmy w tym ćwiczeniu są w miarę prawidłowe. Świadczą o tym wykreślone przeze mnie na ich podstawie charakterystyki. Napięcie na rezystorze przybiera wartość największą dla częstotliwości rezonansowej i częstotliwości z jej okolic. Korzystając z prawa Ohma
widzimy, że dla tych częstotliwości również wartość prądu rezystora jest największa.

Rozpatrując pod tym kątem pozostałe elementy obwodu- cewkę i kondensator, zauważamy, że napięcie na cewce osiąga wartość maksymalną dla częstotliwości wyższej niż rezonansowa. W przypadku kondensatora jest jeszcze inaczej, a mianowicie napięcie na tym elemencie ma wartość największą dla częstotliwości mniejszej niż rezonansowa.

Faktem jest, że maksymalne wartości na cewce i kondensatorze są większe niż napięcie zasilania. Powoduje to powstawanie przepięć w obwodzie. Interpretując uzyskane wyniki dostrzegamy że maksymalne wartości napięć na cewce i kondensatorze są około Q razy większe od wartości napięcia zasilającego.

Z teorii wiemy, że wartość spadku napięcia na rezystancji występująca przy częstotliwości rezonansowej jest równa wartości napięcia zasilającego. Własność tą trudno jednak odczytać z pomiarów ze względu na duże wahania wartości napięcia generatora podczas wykonywania ćwiczenia.

Pomiary wykonywane w ćwiczeniu polegały na spisywaniu wartości napięć na badanym elemencie dla różnych wartości częstotliwości, przy czym musieliśmy kontrolować i dostrajać wartość napięcia wejściowego tak aby jego wartość mieściła się w przedziale od 0,78 do 0,82 [V].

---