193 Rozpraszanie światła w roztworach koloidalnych

Efekt Tyndalla to zjawisko fizyczne polegające na rozpraszaniu światła przez koloid z

wytworzeniem charakterystycznego stożka świetlnego nazwanego efektem (zjawiskiem)

Tyndalla.

Jeżeli przez roztwór koloidalny przepuści się wiązkę światła, to wskutek uginania się

promieni na cząstkach fazy rozproszonej, światło staje się widoczne w postaci tzw. stożka

Tyndalla. Intensywność tego zjawiska jest tym większa, im większa jest różnica między

współczynnikiem załamania fazy rozproszonej i ośrodka dyspersyjnego.

W przypadku wymiarów cząstek znacznie mniejszych od długości fali promieniowania

rozpraszanego λ, natężenie światła rozproszonego IΘ pod kątem Θ do kierunku światła

padającego I0, mierzone w odległości R od rozpraszającej objętości V, wyraża się wzorem:

IΘ = I0·(8π⁴NVα²/λ⁴R²)·(1+cos²Θ),

gdzie:

N - liczba cząsteczek rozpraszających w jednostce objętości,

α - polaryzowalność cząstek rozpraszających, zależna od współczynników załamania światła

dla układu koloidalnego i czystego rozpuszczalnika.

Najsilniej ulega rozproszeniu światło o najkrótszej fali, co stanowi przyczynę błękitnej barwy

nieba (rozproszenie światła na cząstkach atmosferycznych) oraz dymu papierosowego.

197 Chromatografia żelowa

Chromatografia żelowa (sączenie żelowe) jest to metoda stosowana jest do rozdziału głównie białek i wielocukrów ze względu na różnice w ich wielkości i kształcie.

Kolumnę chromatograficzną wypełnia się złożem (faza stacjonarna) w postaci ziarenek o określonej wielkości porów zbudowanych z nierozpuszczalnego polimeru (typu: dekstran, agaroza) lub poliakrylamidu.Po nałożeniu na żel mieszaniny, białka o małych rozmiarach wnikają do wnętrza ziaren duże natomiast nie mogą. Droga do momentu wycieku z kolumny, którą musi pokonać każdy ze składników próbki jest więc nierówna. Cząsteczki o najmniejszym ciężarze cząsteczkowym mają do pokonania najdłuższą drogę i dlatego wypływają najpóźniej z kolumny. Białka o dużej masie cząsteczkowej i o średnicy większej niż pory ziaren złoża mają do pokonania krótszą drogę w żelu i wędrują najszybciej. Pojawiają się zatem jako pierwsze u wylotu kolumny.

198 Dyfuzja makrocząsteczek w roztworze, współczynnik dyfuzji a geometria makrocząsteczek, wzór, rola, przykładowe wartości

Współczynnik dyfuzji D zależy m.in. od rozmiarów i kształtów cząsteczek dyfundujących, tak więc pomiar tego współczynnika może dostarczyć informacji o cechach makrocząsteczek.
Dla cząsteczek kulistych zależność współczynnika D od promienia cząsteczki wyraża wzór:

gdzie: n- lepkość rozpuszczalnika r- promień cząsteczki
k- stała Boltzamana D- współ. Dyfuzji (cm2/s)
T- temperatura

Współczynnik dyfuzji zgodnie ze wzorem jest odwrotenie proporcjonalny do wartości promienia r.
Dzieje się tak ze względu na wytstępujące siły tarcia w roztworach.
Współczynnik ten może się przydać do wyliczenia masy cząsteczkowej (gdy są znane także dane o sedymentacji w ultrawirówce)
-11

Przykładowe wartości: 10 m2/s dla białek a dla substancji małocząsteczkowych ok 10-100 razy większy.


199 I zasada termodynamiki

Przyrost energi wewnętrznej U2-U1 układu jest równy sumie dostarczonego mu ciepła Q i wykonanej pracy, co wyraża się wzorem:
U2-U1=Q+W

Ewentualnie:1. Energia wewnętrzna U układu jest energią związaną z nieuporządkowanym ruchem cząsteczek, zarówno kinetyczną jak i potencjalną ich wzajemnego oddziaływania.
2. Wzór wyżej podany można przestawić w formie (-W)+( U2-U1)=Q wtedy można powiedzieć że ciepło dostarczone układowi zużywa się na wzrost jego energi wewnętrznej i wykonaną przez układ pracę.
Przy dostarczaniu układowi ciepła przyrost energi wewnętrznej zależy od tego czy układ wykonuje pracę. Np: przy ogrzewaniu gazu przy stałej objętości praca nie jest wykonywana W=0 (bo -W=pΔV a zmiana objętości ΔV=0) więc całe ciaepło jest wykorzystywane na wzrost energi wewnętrznej Q=( U2-U1). Gdy jednak układ zmienia objętość to -W=pV a więc Q=( U2-U1)+pΔV

200 - I zasada terodynamiki w układach biologicznych, biokalorymetria pośrednia i bezpośrednia

I zasada termodynamiki jako zasada zachowania energi powinna być zachowana w procesach biologicznych. Energia organizmowi jest potrzeban do zachowania struktury, przeprowadzanai procesów, wykonywania czynności. Pochodzi ona z utleniania produktów pokarmowych przy stałej temperaturze i ciśnieniu. Energia odstarczona nie jest jednak równa entalpi swobodniej ΔG gdyż część energi (76kJ/mol glukozy) wchodzi w skład energi związanej i proces ten nie jest odwracalny. Dlatego za miarę energi dostarczonej przyjmuje się entalpie ΔH.
Kosztem energi ΔH organizm wykonuje pracę wewnętrzną Wi i zewnętrzną We. Praca zewnętrzna kest równa pracy wykonanej kosztem wysiłku mięśniowego. Praca wewnętrzna związana jest z pokonywaniem oporów podczas wielu procesów (krążenie, oddychanie, transport przeciw gradientom stężeń itp) i w końcowym efekcie zamienia się w ciepło Wi=Q.
Bilans Energi wyraża się więc wzorem ΔH= We+Q


Ciepło oddawane przez organizm do otoczenia można mierzyć dzięki kalorymetrom.

1. Biokalorymetria bezpośrednia - obiekt badany znajduje sięw komorze o dokładnej izolacji cieplnej. Ilość ciepła wytworzoną w komorze mierzy się ilością ciepła pobraną przez wodę przepływającą przez system rur znajdujący się w komorze.
Mierząc masę m przepływającej wody i przyrost jej temperatury ΔT ilość ciepła obliczymy ze wzoru: Q=cmΔT.
Wielkość wykonanej pracy We mierzy się za pomocą cykloergometru (przypomina rower)
Energię którą organizm otrzymuje, mierzy się energią którą organizm pobrał w procesach utleniania związków pokarmowych (przydatne tabele wykorzystania energi przez organizm z utlenienia danego związku)

Kalorymetr ten pozwala także zmieżyć ilość zużytego przez organizm tlenu i wydalonego CO2, a wiedząc ile tlenu się zużywa na spalenie określonej ilość związku i ile względnie powinno w tym procesie powstać CO2 można obliczyć ciepło metabolizmu.

2. Kalorymetria pośrednia - polega na pomiarze ilości pobranego tlenu i wydalonego CO2, wykorzystuje siędo tego maskę/ustnik oddzielający powietrze wydychane i wdychane. Obliczenie ciepła metabolizmu wymaga jednak znajomości jaki składniki został utleniony. Określić to pomaga iloraz oddechowy RQ, wyraża się on stosunkiem objętości wydalonego przez organizm dwutlenku węgla Vco2 do objętości pobranego tlenu Vo2 : RQ= Vco2 /Vo2
Stosunek oddechowy dla węglowodanów wynosi 1 dla tłuszczów 0,71 a białek 0,81

Pomiary kalorymetryczne pozwalają zmierzyć:

• wydajność z jaką organizm przekształca energię chemiczną na pracę mechaniczną (wartość w granicach 20-25%, gdyż jest to stosunek wykonanej pracy wewnętznej We do zużytej na ten cel energi ΔHe a nie do całej pobranej energi)

• przemianę podstawową materii - najmniejszą moc energii jaką organizm potrzebuje do utrzymania procesów życiowych będąc w całkowitym spoczynku. Przemiana ta wynosi średnio 80W = 1700 kcal/24h

201. II zasada Termodynamiki

Za wielkość określającą stan uporządkowania układu można przyjąć wprowadzoną przez Boltzmanna wielkość S proporcjonalną do ln W (liczba mikrostanów wyrażająca liczbe sposobów wg. Ktorych z elementow mikroskopwych daje sie zrealizowac dany stan makroskopowy układu)

Więc:

S=k*lnW

Gdzie: k - stała Bolzmanna

S- jest funkją stanu zwaną jako entropia

Entropia jest funkcją stanu określającą w jakim kierunku mogą zachodzić procesy w układnie izolowanym.

Jeżeli entropia początkowo była S₁= k lnW₁ a końcowo S₂= k lnW₂ to przy przejsciu ze stanu 1 do stanu 2 entropia układu zmieni się o

ΔS= S₂-S₁ = k ln W₂/W₁=k ln P₂/P₁

W układzie izolowanym proces zmierza w kierunku od mniejszego prawdopodobieństwa P₁ do większego P₂, od Mniejszego nieporządku W₁ do większego W_2..

Wobec tego P₂>P₁ oraz W₂>W₁ . Musi być:

S₂ > S₁

ΔS > 0

W układzie izolowanym procesy mogą zachodzić tylko w kierunku wzrostu Entropii ; w stanie równowagi entropia przyjmuje wartość stałą maksymalną.

ΔS=0 S=Smaks -> w stanie równowagi

Jest to treść drugiej zasady termodynamiki

Clausjusza.

Wg Clausjusza doprowadzenie do układu ciepła w ilości dQ przy temp. T w sposób quasi-statyczny powoduje wzrost entropii układu o

dS =
proces quasi-statyczny

Jeżeli temp układu zmieni sie podczas dostarczania ciepła zmiana entropii ΔS układu wyrazi sie wzorem

ΔS = S₂-S₁ =

Poglądowo interpretacja wygląda tak: Dodanie ciepła w ilości dQ oznacza dodanie nieporządku co powoduje wzrost entropii. W im wiekszej temp to zachodzi tnz. Przy im wiekszym stanie nieporządku dodamy go jeszcze troche tym mniejsze to powinno miec znaczenie dla entropii, czego odpowiednikiem jest T w mianowniku . Dotyczy to procesow odwracalnych

Nieodwracalne psuja porządek na wlasna reke przyrost entropii jest wiec wiekszy od tego spowodowanego odwracalnym dodaniem ciepła dQ. Czyli:

dS =
lub dS = dSe + dSi

Na przyrost entropii składa sie : przyrost dSe wynikający z dodania ciepła dQe ; oraz przyrost dSe( tak jest w książce chociaż ja mam wrażenie że powinno tu być dSi) będący wynikiem procesów nieodwracalnych. Ciepło dQi zwane jest ciepłem nieskompensowanym - wytworzone w procesach dyssypacyjnych, rozpraszajacych energie w wyniku pokonywania oporow np tarcia.

Zawsze jest dSi = dQi / T > 0

Wyrazenie dS =
lub dS = dSe + dSi mozna uznac za ogólne sformułowanie drugiej zasady termodynamiki .

Układ izolowany dQe = 0

Proces quasi statyczny dSi = 0 Proces nieodwracalny dSi > 0

dS=0 S=const dS>0 S₂>S₁

W układzie izolowanym entropia nie może maleć dS ≥ 0

Wymieniajacy ciepło z otoczeniem dQe ≠ 0

Proces q s : dSi = 0 Proces nieodwracalny dSi > 0

dS =
dS >

W układach wymieniajacych ciepło z otoczeniem przyrost entropii dS nie moze byc mniejszy od

dS ≥

202 II zasada w układach biologicznych

Entropia organizmu żywego stanowiącego układ otwarty zmienia sie zgodnie z szybkością

=
gdyby organizm był układem zamknietym po pewnym czasie organizm znalazłby sie w stanie równowagi statycznej rownoważnej ze śmiercią.

Organizm stanowiąc układ otwarty wymienia entropie dSe z otoczeniem ; otrzymuje bowiem entropie

dS'e > 0 z pokarmem oraz oddaje dS''e < 0 wraz z zdegradowanymi produktami przemiany materii i zdegradowana energią ( w postaci ciepła). Wymieniona z otoczeniem entropia dSe jest ujemna :

dSe = |dS'e| - |dS''e| < 0 bowiem |dS'e| < |dS''e| . Rownoczesnie w organizmie zachodzą procesy nieodwracalne tworzace entropie dSi. W organizmie dojrzalym nie zmieniającym biomasy szybkosc tworzenia entropii jest rowna szybkosci oddawania dSi/dt = |dSe /dt|

Entropia organizmu nie zmienia sie w czasie dS_org/dt = 0 , S_org= const. Organizm znajduje sie w stanie stacjonarnym.:

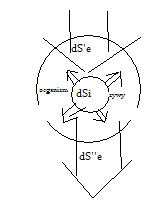
Model org żywego w stanie stacjonarnym. (jakby co rysunek 6.2 strona 150 Pilawski)

W stanie stacjonarnym stale czynne sa procesy nieodwracalne destrukcyjne tworzące entropie . Procesom tym przeciwstawiaja sie procesy konstruktywne zwiazane z wymiana entropii z otoczeniem zmniejszające entropie.

;Stwierdzono doświadczalnie ze młode organizmy w rozwoju odddaja wiecej ciepła do otoczenia , odznaczają sie większą dyssypacją energii niż organizmy dojrzałe . Znaczy to że w stanie rozwoju żródło entropii jest wieksze od wymaganego zasada Prigogine'a minimum . Swiadczy to o zywiej zachodzacych procesach metabolizmu i o wiekszej aktywnosci organizmu. Mozna zaryzykowac stwierdzenie ze szybkosc produkcji entropii jest miara zywotnosci organizmu. Stąd wniosek ze dla utrzymania wiekszej zywotnosci , dla zachowania mlodosci nalezy zwiekszyc procesy metabolizmu, prowokujace zwiekszenie produkcji entropii, prowokujace zarazem org. Do walki z nia. Uzyskuje sie to przede wszystkim aktywnoscia fizyczna. Wysiłek wzmaga procesy transportu zwiekszajac z jednej strony zrodlo entropii a z drugiej zwiekszajac zapotrzebowanie na energie i materie (pokarmy)

Utrzymanie organizmu przy zyciu okupione jest wzrostem entropii otoczenia . Jesli za układ uwazac organizm i otoczenie bedzie to uklad izolowany. Zgodnie z 2 zasada termodynamiki entropia w takim ukladzie moze tylko rosnac : ΔS_przyrody = ΔS_org + ΔS_otoczenia > 0

203. III zasada termodynamiki

Sformulował ją Nernst : dla układów skondensowanych (ciala stałe i ciecze) entropia staje sie zerem w temperaturze zera bezwzględnego .

Postulat ten uogólnił Planck: entropia każdego ciała doskonale jednolitego jest zerem w temp zera bezwzględnego.

Lim S = 0

T->0

Postulat wywodzi sie z zaleznosci S = k lnW

Ciało doskonale jednolite to ciało ktorego uporzadkowanie w zerze bezwzglednym jest doskonale to znaczy że W = 1 czyli S = 0

Wynikaja z tej zasady ważne wnioski np możliwośc obliczenia bezwzględnej wartosci entropii ciał dla ktorych jest spełniona

204. Równania fenomenologiczne

Bodzce wywołują transport odpowiednio: energii, substancji, ładunku elektrycznego. Zjawiska te podlegaja prawom:

prawo fouriera przewodzenia ciepła ( s - powierzcnia
- przewodność cieplna własciwa ,

dT/dx - spadek temperatur)

prawo Ficka dyfuzji

prawo Ohma przewodzenia pradu ( dq/dt -prad elektr,
- przewodnosc elektr wlasciwa,

dV/dx - spadek pot. Elektr)

Oznaczając bodźce termodynamiczne ogolnie przez Xi oraz przyporządkowane im przepływy przez

Ji =
(gestość strumienia odpowiednio : ciepła przy di= dQ, substancji przy di=dn, ładunku elektrycznego przy di = dq)

Prawa te mozna ogólnie ując jednym wzorem J_i = L_iX_i (Li - wspolczynnik proporcjonalnosci

charakteryzujący dane zjawisko , wyraza

liczbowo przeplyw odpowiadajacy bodzcowi jednostkowemu)

Transport opisany tym wzorem jest raczej uproszeczniem, na ogoł w ukladzie dziala nie jeden a wiecej bodzców wzajemnie od siebie zaleznych. Pojawiają sie wtedy przeplywy wymuszone zwane sprzezonymi powodujac pojawienie sie nowych bodzców. Np bodziec temp w mieszaninie gazów poza transportem energii powoduje wturnie transport dyfuzyjny - termodyfuzje.

Wtedy kazdy przeplyw Ji jest funkjcą nie tylko bodzca Xi ktoremu jest przyporzadkowany ale tez funkcją pozostalych bodzców.

Ji = f(X₁,X₂,...,X_i...,X_n)

Przyjmuje sie ze funkcje te są liniowe co jest uzasadnione w stanie niezbyt odleglym od równowagi. Mozna wtedy napisac równania

Ji = L_i1X₁+ L_i2X₂...+ L_iiX_i... L_inX_n, i=1,2...n

Rownan takich jest n po jednym dla kazdego przepływu J₁,...J_n - nazywa sie je równaniami fenomenologicznymi. Wspolczynniki L zwane wspolczynnikami fenomenologicznymi charakteryzują zachodzące procesy transportu. Jest ich n² . Wg onsagera wspolczynniki symetryczne sa sobie rowne L_ik=L_ki

Wtedy liczba charakteryzują proces ogranicza sie do ½ (n²+n)

Przy 2 bodzcach np. J₁= L₁₁X₁+L₁₂X₂

J₂= L₂₁X₁+L₂₂X₂ Proces charakteryzuja 3 wspolczynniki L₁₁,L₂₂, L₂₁=L₁₂

PYTANIE 205 ENTROPIA

Entropia- funkcja stanu określająca stan uporządkowania układu, która zgodnie ze wzorem Boltzmanna jest proporcjonalna do lnW, a więc:

S= k*lnW gdzie: k- stała Boltzmanna

W- liczba mikrostanów, wyrażająca liczbę sposobów

według których z elementów mikroskopowy

daje się zrealizować dany stan makroskopowy

układu. Stan makroskopowy gazu jest

opisany parametrami mierzalnymi (ciśnienie

temp) które to wielkości są wynikiem

uśredniania wielkości mikroskopowych (pędy

cząsteczek, ich energie). Miara nieporządku w

stosowana w termodynamice.

Wcześniej entropia została wprowadzona przez Clausjusza na podstawie rozważań Carnota dotyczących sprawności motorów cieplnych.

Entropia określa w jakim kierunku mogą zachodzić procesy w układzie izolowanym. Jeżeli entropia układu w stanie początkowym była S₁= k*lnW₁ a w stanie końcowym S₂=k*lnW₂ to przy przejściu ze staniu początkowego do końcowego entropia układu zmieni się o:

ΔS=S₂-S₁= k*lnW₂/W₁= k*lnP₂/P₁

W układzie izolowanym proces zmierza od prawdopodobieństwa mniejszego P₁ do prawdopodobieństwa większego P₂ czyli od mniejszego nieporządku W₁ do większego W₂. Skoro więc P₂>P₁ oraz W₂>W₁ to:

S₂>S₁

ΔS>0

W układzie izolowanym procesy mogą zachodzić tylko w kierunku wzrostu entropii. W stanie równowagi entropia przyjmuje wartość stałą maksymalną (II zasada termodynamiki):

ΔS=0 S=S_max (stan równowagi)

PYTANIE 206 ENTROPIA A WYMIANA CIEPŁA

I. Procesy odwracalne

Jeśli doprowadzimy do układu ciepło w ilości dQ przy temperaturze T w sposób quasi-statyczny (odwracalny) to nastąpi wzrost entropii układu o:

dS= dQ/T

Jeżeli temp. układu zmieni się w czasie dostarczania ciepła to zmiana entropii układu wyrazi się wzorem:

_T2

ΔS= S2-S1= ƒ dQ/T

^T1

Z powyższej zależności wynika, że dodanie ciepła do układu w ilości dQ jest równoznaczne z dodaniem nieporządku (nieuporządkowany ruch cieplny) z czym wiąże się wzrost entropii. Jednak w im wyższej temperaturze proces ten zachodzi tym mniejsze ma to znaczenie dla entropii (świadczy o tym T w mianowniku)

II. Procesy nieodwracalne

W procesach nieodwracalnych przyrost entropii będzie większy od tego, który wby był spowodowany odwracalnym dodaniem ciepła dQ (dyż procesy te „psują” porządek na własną rękę) co wyraża wzór:

dS= dQe/T + dQi/T lub po prostu dS=dSe+dSi

Zatem jak wynika z wzoru na przyrost entropii układu składa się przyrost dSe wynikąjący z dodania ciepła w ilości dQe oraz przyrost dSi wynikający z procesów nieodwracalnych, w których ciepło dQi (ciepło nieskompensowane) to ciepło wytworzone w procesach dyssypacyjnych, rozpraszających energię w wyniku pokonywania oporów (tarcie, lepkość itp.) Należy pamiętać, że przyrost dSi jest zawsze większy od 0.

Dla układu izolowanego (dQe=0)

proces quasi statyczny: dSi=0 proces nieodwracalny: dSi>0

dS=0 S= const dS>0, S2>S1

Wniosek: W układzie izolowanym entropia nie może maleć.

Dla układu wymieniającego ciepło z otoczeniem (dQe≠0)

proces quasi- statyczny: dSi=0 proces nieodwracalny dSi>0

dS=dQe/T dS>dQe/T

Wniosek: w układach wymieniających ciepło z otoczeniem przyrost entropi dS nie może być mniejszy od dQe/T.

W układach wymieniających ciepło z otoczeniem przyrost entropii dS może być większy lub mniejszy od zera, może też być zerem. Zależy to od znaku oraz od wartości entropii dSe wymienionej z otoczeniem.

PYTANIE 207 ENERGIA WEWN I ENTALPIA- ich zachowanie się w procesach endo i egzetermicznych.

Ze względu na ciepło, które układ wymienia z otoczeniem reakcje chemiczne można podzielić na endotermiczne i egzotermiczne. Ciepło to zależy od tego czy reakcja zachodzi izochorycznie czy izobarycznie. W pierwszym przypadku miarą ciepła reakcji jest zmiana energii wewnętrzenej ΔU (V=const), a w drugim zmiana entalpii ΔH (p=const). Rozróżnianie energii wewn i entalpii jako miar ciepła jest konieczne tylko w przypadku gazów, natomiast w przypadku cieczy i ciał stałych praktycznie ΔU= ΔH ze względu na małe zmiany objętości.

1. reakcja jest egzotermiczna jeżeli ΔU<0 albo ΔH<0 czyli gdy układ oddaje energię do otoczenia.

2. reakcja jest endotermiczna jeżeli ΔU>0 albo ΔH>0 czyli gdy układ pobiera energią z otoczenia.

PYTANIE 208 ENERGIA SWODOBNA ENTALPIA SWOBODNA.

W procesach zachodzących izotermicznie kierunek ich przebiegu wyznacza energia swobodna F (w przemianach izochorycznych) oraz entalpia swobodna G (w przemianach izobarycznych.

Energia swobodna wynika z pierwszej i drugiej zasady termodynamiki, gdyż zgodnie z 1 zasadą: ΔU= ΔQ+ΔW czyli (-ΔW)= (-ΔU) + ΔQ, gdzie: (-ΔW)- praca wyk przez układ

(-ΔU)- ubytek energii wewnętrznej

ΔQ- ciepło wymienione z otoczeniem

Natomiast zgodnie z 2 zasadą termodynamiki ΔQ≤ T*ΔS (znak równości dotyczyłby procesów odwracalnych, a nierówności procesów nieodwracalnych), zatem:

(-ΔW)≤ (-ΔU)+ (T*ΔS)

Powyższy wzór dla procesów izotermicznych przyjmuje postać:

(-ΔW)≤ -Δ(U-TS) dla T=const

Zatem o pracy jaką może wykonać układ decyduje wielkość F:

F= U- TS

Powyższy wzór dla procesów izotermicznych może przyjąć postać:

ΔF= ΔU- T*ΔS

Wielkość F nazwana jest energią swobodną

W procesach izotermicznych ubytek energii swobodnej (-ΔF) jest równy pracy wykonanej przez układ (-ΔW), jeżeli proces przebiega odwracalnie; jest natomiast większy od pracy wykonanej, jeżeli proces jest nieodwracalny. Ubytek energii swobodnej układu wyraża więc maksymalną pracę, jaką może wykonać układ:

(-ΔF)= (-ΔW).

W procesie nieodwracalnym tylko część energii swobodnej ΔF'< ΔF zostaje wykorzystana jako praca, zaś reszta ΔF- ΔF'= ΔQ' zostaje rozproszona w postaci ciepła (tzn. zjawisko dyssapacji energii).

Z wzoru U=F+TS wynika, że niecała energia wewn. może być wykorzystana do wykonania pracy, a tylko jej część równa energii swobodnej F= U- TS, zaś pozostała część (TS) to energia związana, będąca energią nieużyteczną, która nie nadaje się do wykonania pracy. Energia swobodna F stanowi więc tę część energii wewn. układu, która w odpowiednich warunkach może być wykorzystana jako praca.

Jeżeli układ nie wykonuje pracy, nawet objętościowej to ΔW=0, proces przebiega izochorycznie, gdyż ΔV=0, więc zależność (-ΔF)= (-ΔW) przyjmie postać:

ΔF≤0

Zależność ta mówi o tym, że wyłączając zachodzące w układzie procesy odwracalne, dla których energia swobodna układu zachowuje wartość stałą, procesy izotermiczno- izochoryczne mogą przebiegać samorzutnie wyłącznie w kierunku zmniejszania się energii swobodnej (ΔF<0). Przyjmuje ona wartość najmniejszą w stanie równowagi. W ten sposób udowodniliśmy, że energia swobodna wyznacza kierunek procesu a ponadto stan równowagi układu.

Entalpia swobodna G

Entalpia swobodna zwana także potencjałem termodynamicznym Gibbsa lub potencjałem termodynamicznym pełni podobną rolę w procesach izotermiczno-izobarycznych co energia swobodna w procesach izotermiczno- izochorycznych.

Na pracę w procesie izobarycznym składa się praca objętościowa wykonana przez układ: (-ΔWobj)= pΔV, a ponadto układ może wykonać jakąś inną pracę (-ΔWi). Wówczas całkowita praca wykonana przez układ będzie wynosiła:

(-ΔW)= pΔV+ (-ΔWi), a po przekształceniu otrzymamy, że praca nieobjętościowa wykonana przez układ wynosi:

(-ΔWi)= (-ΔW)- pΔV

Jeśli podstawimy za (-ΔW) wyrażenie (-ΔW)≤ (-ΔU)+ (TΔS) to dla procesów izotermiczno-izobarycznych można otrzymać zależność:

(-ΔWi)≤ -Δ(U+ pV- TS), gdzie U+ pV= H to entalpia układu, zatem:

(-ΔWi)≤ -Δ(H-TS).

Wilekość G= H-TS nazywa się entalpią swobodną, która dla procesów izotermicznych może przyjąć postać:

ΔG= ΔH- TΔS

Korzystając z powyższego wzoru i wiedząc, że (-ΔWi)≤ -Δ(H-TS) można otrzymać zależność:

(-ΔG)≥(-ΔWi ) dla T=const i p=const

Z powyższego wzoru wynika treść fizyczna funkcji G: W procesach izotermiczno- izobarycznych ubytek entalpii swobodnej jest równy pracy nieobjętościowej (-ΔWi) wykonanej przez układ w procesie odwracalnym, jest natomiast większy od tej pracy, jeżeli proces przebiega nieodwracalnie.

Gdy układ poza pracą objętościową nie wykonuje innej pracej wtedy:

(-ΔG)> 0

Z zależności tej (pomijając procesy odwracalne) wynika następujące prawo: Procesy izotermiczno- izobaryczne mogą w układzie przebiegać samorzutnie wyłącznie w kierunku zmniejszania się entalpii swobodnej. Przyjmuje ona wartość najmniejszą w stanie równowagi układu.

---