ĆWICZENIE 41

HYDRODYNAMIKA CIECZY DOSKONAŁEJ

Ciecz doskonała (idealna), nie istniejąca w rzeczywistości, jest to ciecz nieściśliwa pozbawiona lepkości, to znaczy taka, której cząstki mogą przesuwać się wśród innych sąsiednich bez oporu.

• Prawo ciągłości przepływu (strumienia):

Prawo to dotyczy prędkości przepływu cieczy idealnej w poziomym przewodzie o sztywnych ścianach i niejednakowym w różnych miejscach przekroju. Ponieważ ciecz jest nieściśliwa, w danej jednostce czasu ∆t przez każdą część przewodu musi przepływać jej jednakowa objętość ∆V. Jeżeli pola przekroju poprzecznego w różnych miejscach przewodu nazwiemy S₁ i S₂, to stosunek tych przekrojów i prędkości v₁ i v₂ cząsteczek cieczy podczas przesuwania się przez nie będzie się przedstawiał następująco:

albo inaczej

Jest to treść prawa ciągłości, które wyrażone słowami brzmi: prędkość przepływu cieczy w sztywnym przewodzie jest odwrotnie proporcjonalna do pola przekroju poprzecznego w danym miejscu.

Stosunek objętości cieczy ∆V, która przepływa przez dowolny przekrój przewodu w czasie ∆t nazywamy natężeniem przepływu:

Zgodnie z prawem ciągłości przepływu możemy powiedzieć, że w rozważanym przypadku natężenie przepływu jest stałe.

• Prawo Bernoulliego:

Prawo to określa rozkład ciśnień i prędkości cieczy idealnej w rurze o zmiennym przekroju, nachylonej do podłoża pod pewnym kątem, a zatem w różnych miejscach znajdującą się na różnej wysokości.

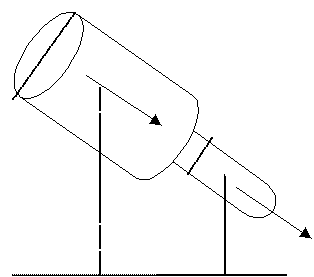
Rozważmy dwa przekroje rury — S₁ i S₂ i odpowiadające im wielkością przekroje S₁' i S₂'. W przekroju S₁ panuje ciśnienie p₁, a w przekroju S₂ — ciśnienie p₂. W ciągu krótkiego czasu objętość cieczy przesunie się z obszaru S₁-S₂ do S₁'-S₂'. Zmiana, której doznała wzięta pod uwagę część cieczy, jest taka, jak gdyby w czasie ∆t ciecz zawarta w walcu S₁-S₁' przeniosła się do walca S₂-S₂', przy czym oczywiście obie objętości są równe. Na pewno jednak zmienia się energia cieczy — ciecz w walcu S₁-S₁' znajdowała się wyżej (h₁), pod innym ciśnieniem (p₁) i miała mniejszą prędkość (v₁) niż ciecz w walcu S₂-S₂'. Dla cieczy idealnej możemy zastosować zasadę zachowania energii mechanicznej i napisać, że energia kinetyczna masy cieczy zawartej w objętości S₂-S₂' wzrosła kosztem pracy ciśnień p₁ i p₂ oraz kosztem ubytku energii potencjalnej, czyli:

(gdzie h₁ i h₂ są wysokościami środków ciężkości cieczy w S₁-S₁' i S₂-S₂').

Po przekształceniu powyższej równości otrzymujemy:

dla każdego przekroju.

Podstawiając do tego wzoru m = Vρ, gdzie ρ oznacza gęstość cieczy, otrzymamy:

Jest to treść prawa Bernoulliego, mówiącego, że suma ciśnień statycznego (p), hydrostatycznego (hρg) i hydrodynamicznego (
) jest w danym przepływie dla dowolnego przekroju wielkością stałą.

Możemy wyróżnić dwa przypadki szczególne tego prawa:

1. kiedy ciecz płynie przez przewód poziomy. Prawo Bernoulliego przybiera wtedy prostszą postać:

2. kiedy ciecz płynie w naczyniu pionowym. Wówczas p₁ = p₂, gdyż u góry i u dołu działa to samo ciśnienie atmosferyczne. Z równania Bernoulliego otrzymujemy wtedy:

Zakładając, że przekrój zbiornika jest duży w porównaniu z przekrojem rury odpływowej, możemy napisać, że v₁ = 0. Oznaczając v₂ jako v i (h₁ - h₂) jako h zbiornika, otrzymujemy:

Jest to znany wzór Torricellego, określający prędkość wypływu cieczy z naczynia pod wpływem własnego ciężaru.

CIECZ RZECZYWISTA. LEPKOŚĆ CIECZY

Ciecze rzeczywiste są „lepkie”. Oznacza to, że między dwiema warstwami cieczy, poruszającymi się względem siebie, występują siły styczne pochodzenia cząsteczkowego. Konsekwencją istnienia tych sił jest fakt, że poruszająca się warstwa cieczy wpływa na ruch warstw sąsiednich.

Rozważmy warstwę cieczy zawartą między dwoma szklanymi płytkami. Możemy ją umownie podzielić na szereg cieńszych warstw, równoległych do obu płytek. Jeżeli na płytkę górną podziałamy siłą F styczną do powierzchni, przesunie się ona z prędkością v₁. Z taką samą prędkością v₁ przesunie się pierwsza warstewka cieczy. Druga warstewka będzie miała nieco mniejszą prędkość v₂, trzecia — jeszcze mniejszą prędkość v₃ itd. Jak wykazał Newton, siła działająca między tymi warstwami jest proporcjonalna do powierzchni ich zetknięcia S oraz do spadu (gradientu) prędkości.

gdzie
oznacza gradient prędkości (∆v oznacza różnicę prędkości, a ∆x — wzajemną odległość warstw).

Współczynnik η w powyższym wzorze jest zwany współczynnikiem lepkości (albo po prostu lepkością cieczy), zależnym od rodzaju cieczy i od temperatury. Jest on liczbowo równy sile potrzebnej do podtrzymania ruchu, gdy powierzchnia styku warstw jest jednostkowa
(1 m²), podobnie jak gradient prędkości. Jednostką współczynnika lepkości jest:

Współczynnik η omawiany powyżej to tzw. współczynnik lepkości dynamicznej, inaczej zwany bezwzględnym współczynnikiem lepkości.

Czasem mówi się także o względnym współczynniku lepkości — jest to stosunek lepkości badanej cieczy do lepkości innej cieczy, zwanej wzorcową (często jest nią woda o temp. 20˚C, której η wynosi 0,001 Pa · s).

Istniej również współczynnik lepkości kinematycznej v, równy stosunkowi współczynnika lepkości dynamicznej η do gęstości cieczy ρ.

A oto jego jednostka:

Współczynnik lepkości cieczy zmienia się w przybliżeniu wykładniczo wraz ze wzrostem temperatury.

gdzie A i B są współczynnikami w niewielkim stopniu zależnymi od temperatury,

k oznacza stałą Boltzmanna,

a T — temperaturę bezwzględną (w skali Kelvina).

Przy obniżaniu temperatury lepkość wszystkich cieczy wzrasta. Jedynym wyjątkiem jest skroplony hel, oziębiony do temperatury 2,17˚K, zwany helem II, którego lepkość staje się niemierzalnie mała. Zjawisko to nosi nazwę nadciekłości (nadpłynności).

PRZEPŁYW CIECZY RZECZYWISTEJ PRZEZ PRZEWODY. PRAWO POISSEUILLE'A - HAGENA.

Przepływ cieczy lepkiej przez przewody różni się od przepływu cieczy doskonałej. Prędkości przepływu poszczególnych warstw cieczy w przewodzie nie są jednakowe: struga przyosiowa ma prędkość największą, malejącą ku ściankom przewodu, zaś warstwy cieczy na samych ściankach mają prędkość równą zeru.

Gdy ciecz lepka płynie w przewodzie o stałym przekroju, ciśnienie statyczne wzdłuż przewodu stopniowo maleje. Na skutek lepkości praca ciśnienia częściowo zużywa się na pokonanie oporów wynikających z hamowania warstw o większej prędkości przepływu przez warstwy powolniejsze i zamienia się na ciepło.

Chcąc wyznaczyć wartość siły lepkości, musimy ocenić wartość rozproszonej energii. Wiemy, że na każdym odcinku przewodu następuje pewien spadek ciśnienia. Nazywamy go gradientem ciśnienia — jest on równy stosunkowi różnicy ciśnień na końcach odcinka do jego długości. Gradient ciśnienia jest proporcjonalny do siły lepkości F i może służyć za miarę straty energii mechanicznej jednostki objętości cieczy przy jej przesunięciu na drodze l.

gdzie V jest objętością cieczy, a
gradientem ciśnień.

Przepływem cieczy lepkiej przez rurki włoskowate rządzi prawo Poiseuille'a - Hagena. Otrzymujemy je w wyniku rozważań teoretycznych przedstawionych poniżej.

Badamy przepływ cieczy lepkiej przez wąską rurkę (kapilarę). Zakładamy, że ciecz płynąca w kapilarze jest tzw. cieczą niutonowską, to znaczy taką, dla której współczynnik lepkości
η = const i która jest nieściśliwa (jej gęstość ρ = const). Ponadto przyjmujemy, że ruch cieczy jest ruchem stacjonarnym, tj. takim, w którym a = 0, a prędkość warstwy cieczy przylegającej do ściany rury v także równa jest 0. Kapilara, w której ciecz płynie, ma promień R. Do przeprowadzenia obserwacji wybieramy jej odcinek o długości l. Zaniedbujemy wpływ sił grawitacji na przepływ cieczy.

Matematyczne wyprowadzenie prawa Poiseuille'a ma dosyć skomplikowaną postać.

Równanie wyjściowe wyprowadzamy z faktu, że suma sił w ruchu stacjonarnym równa się zeru.

gdzie S₁ jest polem przekroju poprzecznego o promieniu r,

S₂ — polem powierzchni pobocznicy walca o promieniu r i długości l,

p₁ — ciśnieniem na początku rozpatrywanego odcinka kapilary

p₂ — ciśnieniem na jego końcu,

η — wartością współczynnika lepkości,

— gradientem prędkości sąsiadujących ze sobą warstw.

Po podstawieniu πr² w miejsce S₁ i 2πrl w miejsce S₂, oznaczeniu (p₁ - p₂) jako ∆p, scałkowaniu równania i uwzględnieniu faktu, że gdy r = R, to v = 0 otrzymujemy następujący wzór na prędkość cieczy:

Widać zatem, że prędkość przepływu cieczy przez kapilarę jest funkcją odległości r badanej warstwy cieczy od osi walca; widzimy również, że gdy r = 0 (oś walca), prędkość ta jest największa, a gdy r = R — prędkość maleje do zera.

Prawo Poiseuille'a dotyczy konkretnie natężenia przepływu, czyli wydatku (wydatkiem W nazywamy stosunek objętości cieczy przepływającej przez przekrój poprzeczny przewodu do czasu przepływu) dla omawianej kapilary.

Ponieważ wydatek
, po podstawieniu wartości prędkości v i pola powierzchni S przekroju poprzecznego otrzymujemy wzór końcowy:

Wzór ten stanowi treść prawa Poiseulle'a. Zwraca uwagę fakt, że natężenie przepływu (wydatek) zależy od promienia kapilary — dwukrotne zmniejszenie promienia kapilary powoduje szesnastokrotne zmniejszenie natężenia przepływu.

ZASADY POMIARU WSPÓŁCZYNNIKA LEPKOŚCI

• Metoda Stokesa.

Kulkę o znanym promieniu i masie wpuszcza się do szerokiej rury napełnionej badaną cieczą. Ruch kulki, początkowo przyspieszony, przechodzi następnie w ruch jednostajny wskutek wzrostu oporów. Siła ciężkości Q, zmniejszona o siłę wyporu W, równoważy się z siłą oporu środowiska (lepkości) F. Wynika z tego równanie:

F = Q - W

czyli:

gdzie η jest szukaną wartością współczynnika lepkości,

v — szybkością opadania kulki (mierzoną doświadczalnie),

ρ — gęstością kulki,

r — jej promieniem,

ρ₀ — gęstością cieczy,

g — przyspieszeniem ziemskim.

Przekształcając powyższe równanie, otrzymujemy wzór na wartość bezwzględnego współczynnika lepkości η:

• Pomiar za pomocą wiskozymetrów typu Arrheniusa - Ostwalda. Pomiar ten oparty jest na prawie Poiseuille'a i pozwala wyznaczyć względny współczynnik lepkości badanej cieczy.

Zasada pomiaru jest następująca: do prostopadłościennego szklanego naczynia wprowadzamy pionową rurkę kapilarną, na szczycie której umieszczamy zbiorniczek. Na ścianach zbiorniczka oznaczamy poziomy A i B, po czym napełniamy go badaną cieczą i mierzymy czas jej wypływu t_c do dolnego naczynia (korzystamy z oznaczonych na szkle poziomów A i B). Doświadczenie powtarzamy z wodą i otrzymujemy czas wypływu wody t_w. Ponieważ wypływ w obu doświadczeniach jest spowodowany różnicą ciśnień hydrostatycznych słupów obydwu cieczy, a całkowita objętość cieczy, która wypłynęła, jest za każdym razem taka sama, możemy napisać na podstawie wzoru Poiseuille'a:

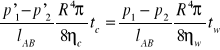
skąd mamy:

Znając gęstość cieczy ρ_c, gęstość wody ρ_w i lepkość wody η_w w danej temperaturze, możemy obliczyć η_c.

• Pomiar za pomocą wizyskometru Hessa, używanego głównie w pomiarach lepkości względnej płynów ustrojowych (np. krwi).

W pomiarze tym pod jednakowym ciśnieniem zasysamy równocześnie badaną ciecz C i wzorcową wodę W przez jednakowe kapilary do rurek R₁ i R₂, kalibrowanych w jednostkach objętości. Na podstawie prawa Poiseuille'a zastosowanego do obu cieczy możemy napisać:

skąd mamy:

gdzie V_w oznacza objętość wessanej wody, a V_c — objętość wessanej cieczy.

RODZAJE PRZEPŁYWU — RUCH LAMINARNY, RUCH BURZLIWY. LICZBA REYNOLDSA

Wyodrębniając w płynącej cieczy wąską strugę, możemy zaobserwować jej przebieg wewnątrz strumienia. Tor strugi wyznacza nam tzw. linię prądu. Jest to krzywa w każdym punkcie styczna do wektora prędkości cieczy w tym punkcie.

Przepływ cieczy, który odbywa się w ten sposób, że poszczególne linie prądu dają się łatwo wyróżnić i przebiegają w przybliżeniu równolegle do siebie, nazywamy laminarnym (uwarstwionym). Jeżeli warunek ten nie jest spełniony, mówimy o przepływie burzliwym.

Przepływowi burzliwemu towarzyszy tworzenie się wirów, w których linie prądu stają się krzywymi zamkniętymi, a prędkości elementów cieczy mogą mieć kierunek przeciwny w stosunku do zasadniczego kierunku przepływu. Wiry te tworzą się tym łatwiej, im większe są gradienty prędkości między sąsiednimi warstwami cieczy — np. przy opływaniu przeszkód itp. Warto zauważyć, że ich powstawanie uwarunkowane jest lepkością cieczy.

Przepływ cieczy badał Reynolds, który stwierdził, że istnieje pewna krytyczna wartość prędkości przepływu, dla której opory wynikające z lepkości cieczy znacznie wzrastają. Przy tej prędkości następuje nagłe przejście przepływu laminarnego w burzliwy. Przy prędkości przepływu mniejszej od krytycznej opory wynikające z lepkości są proporcjonalne do tej prędkości, jeżeli prędkość przepływu przekracza wartość krytyczną — opory te są proporcjonalne do jej kwadratu.

Wzrost oporu tłumaczy się dodatkowymi stratami energii na zużytej na utworzenie wirów. Na skutek działania siły lepkości wiry zanikają, a ich energia kinetyczne przechodzi w ciepło.

Prędkość krytyczną opisuje następująca zależność:

gdzie Re oznacza stały współczynnik zwany liczbą Reynoldsa,

η — współczynnik lepkości dynamicznej,

v — współczynnik lepkości kinematycznej,

D — długość charakterystyczną dla danego przepływu (np. średnicę rury, opływanego ciała itp.,

ρ — gęstość cieczy.

Liczba Reynoldsa jest w przybliżeniu równa wartości stosunku sił bezwładności występujących w przepływie do sił lepkości. Dla cieczy idealnej Re → ∞, dla cieczy bardzo lepkiej, płynącej w wąskim przewodzie, Re → 0.

ĆWICZENIE 42

NAPIĘCIE POWIERZCHNIOWE

Rozpatrując cząsteczki położone wewnątrz i na powierzchni cieczy, zauważamy, że znajdują się one w nieco innych warunkach. Cząsteczki wewnątrz cieczy działają na siebie nawzajem, wskutek czego wypadkowa energia oddziaływań każdej z nich jest równa zeru. Cząsteczki znajdujące się na powierzchni cieczy mają wypadkowe różne od zera, skierowane w głąb cieczy. Chcąc wyprowadzić na powierzchnię nowe cząsteczki (zwiększyć powierzchnię swobodną cieczy), należałoby wykonać pracę między wypadkowej sile wywieranej przez cząsteczki z sąsiadujących warstw głębszych. Oznacza to, że cząsteczki znajdujące się w warstwie powierzchniowej mają pewien zapas energii potencjalnej, tzw. energii powierzchniowej.

Ponieważ stanom równowagi trwałej układów odpowiada minimum energii potencjalnej, każda ciecz swobodna przybiera taki kształt, który dla danej objętości zapewnia minimalną powierzchnię swobodną (a więc i minimalną energię powierzchniową) — dlatego też każda ciecz w stanie nieważkości przybiera kształt kulisty. Kiedy jednak ciecz znajduje się pod wpływem sił grawitacji, powierzchnia jej ulega spłaszczeniu. Energia potencjalna siły ciężkości osiąga minimum, gdy warstewka cieczy jest możliwie najcieńsza, natomiast energia powierzchniowa — gdy ciecz przybierze kształt kuli. Wskutek działania obydwu sił powierzchnia cieczy przybierze kształt pośredni.

Ilość energii powierzchniowej jest w danych warunkach proporcjonalna do wielkości powierzchni swobodnej. Stosunek tej energii do wielkości powierzchni nazywamy bezwzględnym współczynnikiem napięcia powierzchniowego γ:

Jest on liczbowo równy pracy, jaką należy wykonać, aby powiększyć swobodną powierzchnię cieczy o 1 m². Współczynnik γ jest charakterystyczny dla danego rodzaju cieczy, a ściślej mówiąc: dla układu środowisk ciecz - znajdująca się nad nią para; w potocznym ujęciu dotyczy on zatem cieczy i jej własnej pary.

Względnym współczynnikiem napięcia powierzchniowego nazywamy stosunek bezwzględnego współczynnika napięcia powierzchniowego γ do współczynnika napięcia powierzchniowego cieczy, której współczynnik jest znany (np. wody).

Współczynnik napięcia powierzchniowego dla danej substancji w dużym stopniu zależy od temperatury. Ze wzrostem temperatury γ maleje, w przybliżeniu liniowo, do zera. Wartość tę osiąga w temperaturze krytycznej, co w praktyce oznacza zanik powierzchni swobodnej i przejście cieczy w całej swojej objętości w stan gazu.

W warstwie powierzchniowej działają nie tylko siły między cząsteczkami tej warstwy a położonymi głębie — cząsteczki warstwy powierzchniowej oddziałują również na siebie nawzajem, siłami stycznymi do powierzchni cieczy. Noszą one nazwę sił napięcia powierzchniowego.

Rozważymy ramkę z cieniutkiego drutu z napiętą na niej błoną mydlaną, jeden z boków której stanowi ruchoma poprzeczka o długości l, mogąca się poruszać bez tarcia. Chcąc zwiększyć powierzchnię błony, musimy odciągnąć poprzeczkę, działając na nią pewną siłą F. Jeżeli poprzeczkę odciągać będziemy ruchem jednostajnym, wartość siły F będzie równa sile napięcia powierzchniowego błony mydlanej.

Stosunek wypadkowej siły napięcia powierzchniowego F do długości elementu brzegu cieczy l, na który działa ta siła, jest równy współczynnikowi napięcia powierzchniowego cieczy γ.

ZJAWISKO ZWILŻALNOŚCI

Powierzchnia swobodna cieczy zakrzywia się w pobliżu miejsca jej zetknięcia się z ciałem stałym (np. ze ścianką naczynia) i tworzy tak zwany menisk. Zauważmy, że w tym miejscu mamy do czynienia z granicą trzech faz: cieczy (1), ciała stałego (2) i gazu, np. powietrza (3). Na jednostkę długości linii granicznej między tymi fazami działają trzy siły napięcia powierzchniowego (ponieważ mamy trzy pary faz: 1-2, 2-3 i 3-1). Oznaczmy odpowiadające im współczynniki jako γ_1-2, γ_2-3 i γ_3-1.

Kąt α, zawarty wewnątrz cieczy, między ścianką a linią styczną do menisku w punkcie linii granicznej, nazywamy kątem granicznym (kątem zwilżania). Wiemy, że linia graniczna jest w spoczynku, więc wypadkowa sił działających na jej cząsteczki musi być równa zeru. Analizując wartości poszczególnych składowych tej siły, dochodzimy do następującego wzoru:

Ze wzoru wynika, że gdy γ_2-3 = γ_1-2, to zakrzywienia powierzchni nie ma. Jeżeli γ_2-3 > γ_1-2, to
α < 90˚ i menisk jest wklęsły. Ciecz nazywamy wówczas zwilżającą; taki menisk tworzy np. woda na granicy ze szkłem. Jeżeli γ_2-3 < γ_1-2, to α jest kątem rozwartym i menisk jest wypukły. W takim przypadku mówimy, że ciecz nie zwilża ciała stałego. Taki menisk tworzy np. rtęć w naczyniu szklanym.

W przypadku, gdy γ_3-1 jest mniejsze niż γ_2-3 > γ_1-2, wzór traci sens. W takim przypadku linia graniczna nie jest w spoczynku — ciecz rozchodzi się po powierzchni ciała stałego w postaci cienkiej warstwy (dzieje się tak np. z naftą lub czterochlorkiem węgla na szkle).

PRAWO LAPLACE'A

Okazuje się, że konsekwencją występowania zakrzywionych powierzchni cieczy jest powstawanie w jej wnętrzu pewnego dodatkowego ciśnienia dodatniego lub ujemnego. W warunkach równowagi ciśnienie pod powierzchnią wklęsłą jest mniejsze niż pod płaską (powstaje dodatkowe ciśnienie działające w jednym kierunku z ciśnieniem atmosferycznym), a pod wypukłą — nieco większe.

Aby znaleźć wartość różnicy ciśnień między wnętrzem cieczy a jej otoczeniem, posługujemy się wzorem:

gdzie R jest promieniem krzywizny powierzchni cieczy,

a γ — jej współczynnikiem napięcia powierzchniowego.

Wzór ten dotyczy powierzchni kulistej — ponieważ jednak powierzchnia cieczy zazwyczaj nie jest kulista, posługujemy się innym:

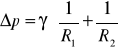
R₁ i R₂ są tak zwanymi głównymi promieniami krzywizny (największym i najmniejszym).

Wzory powyższe noszą nazwę wzorów Laplace'a, które są matematycznym sformułowaniem tzw. prawa Laplace'a.

ZJAWISKO WŁOSKOWATOŚCI

Gdy ciecz znajduje się w naczyniu tak wąskim, że skutek działania sił przylegania między cieczą a ciałem stałym (brzegami naczynia) będzie dostrzegalny na całej powierzchni swobodnej, wówczas ciecz podniesie się lub obniży nie tylko przy ściankach, lecz na całej powierzchni. Naczynia takie nazywamy włoskowatymi (kapilarnymi). Mogą to być np. wąskie rurki o promieniu poniżej 1 mm.

Zjawisko włoskowatości polega na samorzutnym wznoszeniu się lub obniżaniu poziomu cieczy w kapilarach w stosunku do poziomu cieczy w naczyniu, w którym kapilary są zanurzone. Przyczyną takiego zjawiska jest omówiona już różnica ciśnień.

Zjawisko włoskowatości wygląda inaczej dla cieczy zwilżających i niezwilżających. Jeżeli zanurzymy kapilarę w naczyniu zawierającym ciecz zwilżającą, ciecz ta wzniesie się wewnątrz niej wysoko powyżej swojego poziomu w naczyniu. W analogicznej sytuacji ciecz niezwilżająca opadnie wewnątrz kapilary poniżej swojego poziomu na zewnątrz od niej.

Jedno i drugie zjawisko możemy jednak opisać wzorem:

gdzie r oznacza promień rurki włoskowatej

a α jest kątem zwilżania dla danego układu ciecz - ciało stałe.

Powyższa postać wzoru wynika z faktu, że słup cieczy wznosi się lub opada do osiągnięcia takiej wysokości, aby ciśnienie hydrostatyczne (hρg) zrównało się wartością z dodatkowym ciśnieniem dodatnim lub ujemnym powstającym we wnętrzu menisku.

METODY WYZNACZANIA NAPIĘCIA POWIERZCHNIOWEGO

• Metoda kapilarna — polega na wyznaczaniu γ na podstawie zależności:

Wielkościami mierzonymi są tu wysokość słupka cieczy h oraz wewnętrzny promień kapilary r. W metodzie tej ważne jest doskonałe zwilżanie rurki przez ciecz badaną, dlatego też przy pomiarach należy zwracać szczególną uwagę na czystość rurki.

• Metoda stalagmometryczna — opiera się na wypływie kropel cieczy pod wpływem własnego ciężaru z pionowej kapilary. Kropla cieczy może oderwać się od niej wtedy, gdy siły napięcia powierzchniowego F działające na obwodzie rurki o promieniu r zrównają się z ciężarem kropli Q, czyli że 2πrγ = mg. Wówczas możemy wyznaczyć γ z zależności:

Aby dokładnie wyznaczyć masę jednej kropli, liczy się liczbę kropel, które wypłynęły do zlewki z określonej objętości stalagmometru, i waży możliwie dokładnie ciecz, która wypłynęła. Na dokładność tego pomiaru wpływa parowanie cieczy zbierającej się w zlewce.

• Metoda odrywania — polega na zmierzeniu siły potrzebnej do oderwania metalowego pierścienia albo drucika od powierzchni cieczy. Oderwanie następuje wtedy, gdy przykładana przez nas siła F zrównoważy się z siłami napięcia powierzchniowego działającymi po wewnętrznej i zewnętrznej stronie pierścienia. Otrzymujemy wówczas następujący wzór:

przy czym zakładamy, że wewnętrzny i zewnętrzny promień pierścienia r jest taki sam.

ABSORPCJA A ADSORPCJA. SUBSTANCJE POWIERZCHNIOWO CZYNNE

Absorpcją nazywamy wchłanianie jakiejś substancji chemicznej (najczęściej cieczy lub gazu), zwanej absorbatem, przez inną substancję (ciecz lub ciało stałe), zwaną absorbentem, i równomierne rozpuszczanie go w całej masie absorbentu.

Adsorpcją nazywamy gromadzenie się cząstek gazu, pary, cieczy lub rozpuszczonego ciała stałego (również jonów) powierzchni innej cieczy lub ciała stałego, zwanego adsorbentem.

Współczynnik napięcia powierzchniowego danej substancji w bardzo dużym stopniu zależy od jej czystości chemicznej. Obserwujemy to bardzo wyraźnie po dodaniu do wody niewielkiej ilości mydła — zauważamy, że γ znacznie się zmniejsza. Ta zmiana wiąże się ze zjawiskiem adsorpcji cząsteczek mydła na powierzchni swobodnej cieczy. Na powierzchni tej układa się jednocząsteczkowa warstwa, która w istotny sposób zmienia jej stan energetyczny.

W praktyce staramy się nieraz sztucznie obniżyć napięcie powierzchniowe wody, stosując roztwory mydła lub inne, nie zawierające go substancje piorące, tzw. detergenty. Substancje zmieniające γ danej cieczy nazywamy powierzchniowo czynnymi (aktywnymi). Są one często wykorzystywane w gospodarstwie i w technice — np. przy oddzielaniu sproszkowanej rudy od skały płonnej (flotacja).

Aktywność powierzchniową G danej substancji definiujemy zmianą napięcia powierzchniowego wody w zależności od zmiany stężenia c substancji rozpuszczonej.

.

ĆWICZENIE 43

PARAMETRY CHARAKTERYZUJĄCE UKŁAD TERMODYNAMICZNY

Każdy układ termodynamiczny możemy opisać pewnymi parametrami, charakteryzującymi jego stan.

• Parametrami ekstensywnymi układu nazywamy takie, które zależą od wielkości układu i których zmianę trudno spowodować. Należą do nich np. masa i objętość.

• Parametry intensywne to takie, które nie zależą od wielkości układu i których zmiana nie jest trudna w przeprowadzeniu. Są nimi np. stężenie jakiegoś składnika, ciśnienie czy temperatura układu.

BODŹCE I PRZEPŁYWY TERMODYNAMICZNE. POJĘCIE PROCESU.

Pod pojęciem bodźców termodynamicznych rozumiemy czynniki fizyczne warunkujące rozmaite przepływy. Różnica ciśnień (∆p) powoduje przepływ materii, różnica temperatur (∆T) warunkuje przepływ ciepła, a różnica potencjałów elektrycznych (∆V) jest odpowiedzialna za przepływ ładunków elektrycznych. Istniejące w układzie termodynamicznym bodźce tworzą pewien rodzaj uporządkowania, charakteryzujący stan tego układu. Każdy bodziec termodynamiczny powoduje pewien przepływ, czyli przejście układu z jednego stanu w drugi, nazywane procesem.

Każdy przepływ scharakteryzować można dzięki pojęciu strumienia, czyli ilością czynnika transportowanego, która przechodzi w jednostce czasu przez jednostkę powierzchni.

PRAWA DOTYCZĄCE PRZEPŁYWÓW TERMODYNAMICZNYCH. PROCESY ZACHODZĄCE POD WPŁYWEM JEDNEGO BODŹCA TERMODYNAMICZNEGO

Przepływy termodynamiczne spowodowane różnymi bodźcami podlegają rozmaitym prawom. Jednym z nich jest np. prawo Fouriera, czyli przewodzenia ciepła:

gdzie S oznacza powierzchnię przekroju strumienia przepływu,

∆Q — wartość przepływającego ciepła,

∆t — czas przepływu,

λ — przewodność cieplną właściwą,

a
— gradient temperatur na odcinku x.

Innymi takimi prawami są np. prawo Ficka (dyfuzji):

gdzie n oznacza liczbę moli,

D — współczynnik dyfuzji,

a
— gradient stężeń na odcinku x.

czy prawo Ohma (przewodzenia prądu elektrycznego):

gdzie q oznacza ładunek,

γ — przewodność elektryczną właściwą,

a
— gradient potencjałów na odcinku x.

Wszystkie powyższe procesy zaliczamy do takich, w których przepływ powodowany jest działaniem tylko jednego bodźca termodynamicznego (gradientu temperatur, stężeń czy potencjałów). Oznaczając bodźce termodynamiczne ogólnie przez X_i, a przyporządkowane im przepływy przez J_i, gdzie J_i = J_Q (prawo Fouriera), J_c (prawo Ficka) lub J_V (prawo Ohma), powyższe prawa można ująć jednym wzorem:

gdzie L_i jest współczynnikiem proporcjonalności, charakteryzującym dane zjawisko, czyli tak zwanym współczynnikiem fenomenologicznym prostym.

Takie procesy transportu, dające się opisać powyższym prostym wzorem, są bardzo uproszczone. Na ogół w układzie działa nie jeden, a więcej bodźców wzajemnie od siebie zależnych. W takim układzie poza przepływami przyporządkowanymi swoim bodźcom, pojawiają się przepływy wymuszone, zwane przepływami sprzężonymi, a te z kolei powodują pojawienie się nowych bodźców. Każdy przepływ J_i jest funkcją nie tylko bodźca X_i, któremu jest przyporządkowany, ale także wszystkich pozostałych bodźców. Mówimy wówczas o procesach termodynamicznych sprzężonych.

ĆWICZENIE 44

ENERGIA WEWNĘTRZNA UKŁADU

Energia wewnętrzna (U) jest jedną z funkcji stanu układu. Związana jest z nieuporządkowanym ruchem elementów strukturalnych układu, a równa jest sumie energii kinetycznej (E_k) oraz potencjalnej (E_p) wzajemnego oddziaływania składowych elementów układu, zgodnie ze wzorem:

gdzie
, a

Układ mający energię wewnętrzną może jej część, w odpowiednich warunkach, przekazać innemu układowi albo przez wykonanie pracy, albo przez przekazanie ciepła.

I ZASADA TERMODYNAMIKI. ENERGIA WEWNĘTRZNA A ENTALPIA.

Energia wewnętrzna może być przekazywana od jednego układu do drugiego w procesie wykonywania pracy lub przekazywania ciepła. Proces musi przebiegać zgodnie z zasadą zachowania energii — wyraża to pierwsza zasada termodynamiki:

∆U = Q + W

Znakowanie wartości pracy i ciepła:

+Q — gdy doprowadzamy ciepło do układu;

-Q — gdy odprowadzamy ciepło z układu do otoczenia;

+W — gdy wykonujemy nad układem pracę;

-W — gdy praca jest wykonywana przez układ.

Analizując zmiany zachodzące w układzie przy dostarczaniu mu ciepła Q, widzimy, że przyrost energii wewnętrznej może być różny. Zależy to od tego, czy układ wykonał przy tym jakąś pracę (w najczęściej branych pod uwagę przypadkach gazów jest to praca objętościowa, czyli związana ze wzrostem objętości gazu, ale wyróżniamy również inne rodzaje pracy — np. elektryczną czy chemiczną).

Jeżeli nie, całe dostarczone ciepło zamienia się na przyrost energii wewnętrznej (proces izochoryczny):

dla V = const.

Jeżeli natomiast układ wykonał pracę, część dostarczonego ciepła jest zużyta na wzrost objętości (np. proces izobaryczny):

Do opisania takiego układu pojęcie energii wewnętrznej jest niewystarczające, wprowadzamy zatem nową funkcję stanu, zwaną entalpią (H).

Po wprowadzeniu oznaczeń:

i

otrzymujemy inną postać wzoru na ciepło przemiany izobarycznej:

dla p = const.

Przyrost entalpii ∆H jest równy ilości ciepła dostarczonego układowi w procesie izobarycznym, tak jak przyrost energii wewnętrznej ∆U jest równy ilości ciepła dostarczonego układowi w procesie izochorycznym.

DRUGA ZASADA TERMODYNAMIKI. ENTROPIA

W termodynamice jako miarę nieuporządkowania układu przyjmuje się liczbę W mikrostanów, wyrażającą liczbę sposobów, na jakie z elementów mikroskopowych można zrealizować dany stan makroskopowy układu (a, jak wiadomo, dany stan makroskopowy może być realizowany ogromną liczbą różnych mikrostanów). Liczbę W nazywamy prawdopodobieństwem termodynamicznym; jest ono, w przeciwieństwie do prawdopodobieństwa matematycznego (zawsze będącego ułamkiem), liczbą większą od 1.

Jak wynika z analizy prawdopodobieństwa termodynamicznego, w stanie najbardziej prawdopodobne okazuje się istnienie układu o możliwie największym nieuporządkowaniu.

W termodynamice bardziej korzystne okazało się jednak zastąpienie liczby W wprowadzić inną wielkość, oznaczaną jako S, a zwaną entropią — proporcjonalną do ln W, a zatem:

gdzie współczynnikiem proporcjonalności k jest stała Boltzmanna.

Pojęcie entropii jest wygodniejsze od pojęcia prawdopodobieństwa termodynamicznego, ponieważ entropia jest funkcją stanu addytywną, tzn. taką, że jej wartość dla całego układu jest sumą jej wartości dla jego poszczególnych części (S = S₁ + S₂). Wielkość W tej właściwości nie ma.

Entropia jest jedną z najbardziej oryginalnych i uniwersalnych funkcji stanu. Jej pojęciu zawdzięczamy ostateczne sformułowanie drugiej zasady termodynamiki dla układu izolowanego, które w obecnej formie brzmi:

W UKŁADZIE IZOLOWANYM PROCESY MOGĄ ZACHODZIĆ TYLKO W KIERUNKU WZROSTU ENTROPII.

W stanie równowagi entropia przyjmuje wartość stałą, maksymalną.

Jeżeli układ nie jest izolowany, tzn. możemy dostarczać do niego energię w postaci ciepła, II zasada termodynamiki przyjmuje postać:

albo

gdzie Q_e oznacza ciepło doprowadzone do układu z zewnątrz, a Q_i — ciepło wytworzone wewnątrz układu na skutek zachodzących w nim procesów.

Przyrost entropii nigdy nie może być mniejszy od
; w przypadku procesów odwracalnych jest równy wartości tego ilorazu, w przypadku procesów nieodwracalnych — większy od niej.

ENERGIA SWOBODNA I ENTALPIA SWOBODNA

Podobnie jak entropia wyznacza kierunek procesu zachodzącego w układzie izolowanym, bez wymiany ciepła z otoczeniem (czyli adiabatycznie), tak w procesach zachodzących w stałej temperaturze kierunek ten wyznaczają: energia swobodna F (procesy izotermiczno-izochoryczne) i entalpia swobodna G (procesy izotermiczno-izobaryczne).

1. Procesy izotermiczno-izochoryczne:

W procesach elementarnych, jak wiadomo, I zasada termodynamiki przyjmuje postać:

∆U = ∆Q + ∆W

czyli:

(-∆W) = (-∆U) + ∆Q

Z kolei z II zasady termodynamiki wynika, że:

∆Q ≤ T∆S

(znak równości dotyczy procesów odwracalnych, a nierówności — nieodwracalnych).

Po połączeniu obu wzorów otrzymamy:

(-∆W) ≤ (-∆U) + T∆S

a dla procesów izotermicznych:

(-∆W) ≤ -∆(U + TS) gdzie T = const.

O pracy, którą układ może wykonać, decyduje zatem wielkość:

F = -∆(U + TS)

Jest to energia swobodna F.

Sens fizyczny tej wielkości jest następujący: w procesach izotermicznych ubytek energii swobodnej -∆F równy jest pracy wykonanej przez układ -∆W, jeżeli proces przebiega odwracalnie, jest natomiast większy od tej pracy, jeżeli proces jest nieodwracalny. Ubytek energii swobodnej układu wyraża zatem największą pracę, jaką układ może wykonać.

W procesach izochorycznych, jak wiadomo, układ nie wykonuje pracy. Zmiana energii swobodnej zawsze jest zatem mniejsza lub równa zeru. Ponieważ ∆F = 0 jedynie podczas zachodzenia procesów odwracalnych, nie dających zmiany całkowitej energii wewnętrznej układu, analizując pozostałe przypadki otrzymujemy bardzo ważną zależność: procesy izotermiczno-izochoryczne mogą przebiegać samorzutnie wyłącznie w kierunku zmniejszania się energii swobodnej. Przyjmuje ona wartość najmniejszą w stanie równowagi.

2. Procesy izotermiczno-izobaryczne:

Jak wiemy, wartość całkowitej pracy (objętościowej, chemicznej, elektrycznej itp.) dla tych procesów wyraża się wzorem:

(-∆W) = (-∆W_i) + p∆V

Stąd wynika następujący wzór na pracę nieobjętościową (-∆W_i):

(-∆W_i) = (-∆W) - p∆V

Podstawiając do tego równania wyrażenie (-∆W) ≤ (-∆U) + T∆S, otrzymujemy zależność:

(-∆W_i) ≤ -∆(U + pV - TS) gdzie T = const i p = const.

Uwzględniając, że U + pV jest entalpią układu, otrzymujemy:

(-∆W_i) ≤ -∆(H - TS) gdzie T = const i p = const.

O pracy nieobjętościowej, którą układ może wykonać, decyduje zatem wielkość:

G = -∆(H - TS)

Jest to entalpia swobodna G, zwana też potencjałem termodynamicznym Gibbsa albo po prostu potencjałem termodynamicznym.

Sens fizyczny entalpii swobodnej jest następujący: w procesach izotermiczno-izobarycznych ubytek entalpii swobodnej -∆G równy jest pracy nieobjętościowej -∆W_i w procesie odwracalnym, większy zaś od tej pracy, jeśli proces przebiega nieodwracalnie.

Innymi słowy: procesy izotermiczno-izobaryczne mogą w układzie przebiegać samorzutnie wyłącznie w kierunku zmniejszania się entalpii swobodnej. Przyjmuje ona wartość najmniejszą w stanie równowagi układu.

Procesy zachodzące z ubytkiem energii swobodnej lub entalpii swobodnej nazywają się egzoergicznymi, natomiast zachodzące z ich wzrostem — endoergicznymi. Spontanicznie zachodzą w naturze wyłącznie procesy egzoergiczne, spełniające warunek ∆F < 0 lub ∆G < 0. Procesy endoergiczne mogą zachodzić wyłącznie kosztem energii swobodnej czy entalpii swobodnej towarzyszących im procesów egzoergicznych.

Odwrotnie ciecz nieniutonowska to taka, której współczynnik lepkości nie jest stały, a ściśliwość nie jest równa zero. Ciecz niutonowska, aby spełniać te warunki, musi być pozbawiona struktury wewnętrznej i wolna od zawiesin. Ciecze nieniutonowskie nie stosują się ściśle do prawa Poiseuille'a. Przykładem takiej cieczy jest krew.

20218/L → 2374505

S₁

S₁

v₂

v₁

p₂

p₁

h₂

h₁

---