ZASADY DYNAMIKI NEWTONA

I ZASADA DYNAMIKI NEWTONA

Zasada ta jest szczególnym przypadkiem II zasady dynamiki Newtona. Z jej sformułowania wynika, że siła działająca na ciało równa się zeru, a zatem również jego przyspieszenie jest zerowe. Oznacza to, że ciało, na które nie działa żadna siła zewnętrzna lub na które działa układ sił wzajemnie się równoważących, zachowuje swój stan ruchu. Jeżeli pozostawało
w spoczynku, pozostaje w nim nadal, a jeżeli poruszało się, porusza się ruchem jednostajnym po linii prostej, w tym samym kierunku, w którym poruszało się w chwili ustania działania niezrównoważonej siły i z tą samą prędkością, którą w tamtej chwili posiadało.

Z I zasadą dynamiki wiążemy pojęcia układów inercjalnych i nieinercjalnych. Układem inercjalnym nazywamy taki, w którym wszystkie trzy zasady dynamiki są spełnione. Wszystkie inne układy, które pozostają względem niego w spoczynku lub poruszają się ruchem jednostajnym prostoliniowym, również są układami inercjalnymi. W układach nieinercjalnych zasady dynamiki pozornie nie są spełniane — np. dla obserwatora znajdującego się
w ruszającym wagonie pociągu i obserwującego „odrzucanie” pasażerów do tyłu w chwili rozpoczęcia ruchu. Fakt ten z punktu widzenia dynamiki będzie dla niego niezrozumiały, ponieważ nie działa na nich żadna widoczna dla niego siła.

Możemy zatem powiedzieć, że istnieją takie układy odniesienia — układy inercjalne —
w których ciało zachowuje swój stan ruchu (jednostajnego prostoliniowego lub spoczynku) dopóty, dopóki oddziaływania innych ciał (siły) nie zmienią tego stanu. Tę właściwość ciała nazywamy jego bezwładnością, stąd też I zasadę dynamiki Newtona nazywa się też zasadą bezwładności.

II ZASADA DYNAMIKI NEWTONA

II zasada dynamiki Newtona brzmi: Jeżeli na ciało o masie m działa stała siła niezrównoważona, to ciało to porusza się ze stałym przyspieszeniem równym:

.

Przyspieszenie a jest wprost proporcjonalne do wartości działającej siły, a odwrotnie proporcjonalne do masy ciała m.

Oznacza to, że dla każdego ciała stosunek
jest wielkością stałą.

W mechanice newtonowskiej tą stałą wielkością jest masa ciała, charakteryzująca cechę materii zwaną bezwładnością. Im większa bezwładność ciała (a co za tym idzie, jego masa), tym mniejsze przyspieszenie nadawane temu ciału przez tę samą siłę. Masę uważamy zatem za miarę bezwładności ciała.

III ZASADA DYNAMIKI NEWTONA

III zasada dynamiki mówi: Jeżeli dowolne ciało oddziałuje na inne siłą
, to drugie ciało oddziałuje na pierwsze siłą -
, o tej samej wartości bezwzględnej, lecz o przeciwnym zwrocie. Jedną z sił takiej pary,
, nazywamy często akcją, drugą, siłę -
— reakcją.

Zasada ta nie precyzuje zresztą, czy siły te działają wzdłuż tej samej prostej.

Ponieważ siły
i -
działają na różne ciała (są przyłożone do różnych ciał), nie możemy ich dodawać, odejmować ani „równoważyć”. Każda z tych sił działa na inne ciało, nadając mu przyspieszenie lub powodując odpowiednią deformację.

Gdybyśmy mieli do czynienia z wzajemnym oddziaływaniem dwóch ciał swobodnych o masach m₁ i m₂, to w wyniku działania sił akcji i reakcji obydwa uzyskają przyspieszenia (o wartości a₁ i a₂), które spełniać będą warunek:

czyli
.

CIŚNIENIE

Ciśnieniem (p) nazywamy stosunek siły F działającej na element powierzchni o polu S w kierunku prostopadłym do tej powierzchni, do wartości S tego pola. Mierzymy je w paskalach (Pa). Z uwagi na niewielką wartość tej jednostki, w praktyce częściej używa się hektopaskali (1 hPa = 100 Pa) albo kilopaskali (1 kPa = 1000 Pa).

.

Dawniej wartość ciśnienia podawano również w atmosferach lub w milimetrach słupa rtęci.

CIŚNIENIE HYDROSTATYCZNE

Ciśnienie hydrostatyczne powstaje wskutek istnienia pola grawitacyjnego Ziemi. Jest to ciśnienie wywierane przez słup cieczy o określonej wysokości h liczonej od powierzchni swobodnej w głąb cieczy. Na głębokości h wynosi ono:

gdzie h jest wysokością słupa cieczy,

d — jej gęstością,

g — wartością przyspieszenia ziemskiego (ok. 9,8 m/s²)

Gdy gęstość cieczy d jest na każdej głębokości taka sama, ciśnienie hydrostatyczne w danej cieczy jest wprost proporcjonalne do h. Jeżeli uwzględnimy dodatkowo ciśnienie zewnętrzne, np. atmosferyczne P₀, to ciśnienie w cieczy na głębokości h wyniesie:

.

Ciśnienie hydrostatyczne również mierzymy w paskalach (Pa).

POMIAR CIŚNIENIA: BAROMETRY I MANOMETRY

Barometry i manometry są urządzeniami służącymi do pomiaru ciśnienia.

Ciśnienie atmosferyczne mierzymy za pomocą barometru: cieczowego (najczęściej rtęciowego) lub mechanicznego, metalowego (aneroidu). W barometrze rtęciowym wartość ciśnienia atmosferycznego określana jest przez położenie menisku rtęci. Ponieważ jednak gęstość rtęci i długość skali zależą od temperatury (odpowiada za to zjawisko rozszerzalności cieplnej), pomiary ciśnienia w różnych temperaturach nieznacznie różnią się między sobą. Bierzemy na to poprawkę, odejmując od otrzymanej wartości ciśnienia lub dodając do niej wartość ∆p = 0,000163 ∆T · l, gdzie ∆T jest wartością bezwzględną różnicy temperatury otoczenia barometru i temperatury wzorcowej (273˚K), a l — odczytaną wysokością słupka rtęci. Wartość ∆p dodajemy do otrzymanego wyniku, jeżeli temperatura otoczenia barometru jest niższa od temperatury wzorcowej (ciśnienie wskazywane przez barometr jest wówczas zaniżone), odejmujemy ją — gdy temperatura otoczenia barometru jest wyższa od temperatury wzorcowej (wskazanie jest wówczas zawyżone).

Manometrami nazywamy przyrządy używane do pomiaru ciśnienia gazów i cieczy. Wyróżniamy między nimi manometry cieczowe, mechaniczne, elektryczne i inne. Manometry cieczowe (otwarte i zamknięte) mierzą ciśnienia na podstawie prawa naczyń połączonych. Manometry elektryczne wykorzystują zmiany pojemności kondensatorów lub oporu elektrycznego rozmaitych elementów (manometr Piraniego) do wyznaczania wartości ciśnienia w puszce manometrycznej połączonej z obwodem elektrycznym.

PRZEMIANY GAZOWE

I ZASADA TERMODYNAMIKI

I zasada termodynamiki równoważna jest z zasadą zachowania energii i mówi, że zmiana całkowitej energii wewnętrznej układu jest algebraiczną sumą pracy wykonanej przez układ lub nad układem przez siły zewnętrzne i ciepła doprowadzonego do układu lub z niego odprowadzonego.

Poszczególne przypadki tej zasady wyglądają następująco:

1. gdy ∆W = 0 (czyli nie mamy do czynienia z wykonywaniem pracy przez układ ani nad układem). Wówczas ∆U = ∆Q, czyli energia układu może się zmieniać tylko na skutek doprowadzenia do niego ciepła lub odprowadzenia go na zewnątrz.

2. gdy ∆Q = 0 (czyli nie istnieje wymiana energii na drodze cieplnej — mówimy wówczas o tzw. osłonie adiabatycznej układu). ∆U = ∆W, czyli energia układu zmienia się tylko za pośrednictwem pracy.

Znakowanie wartości pracy i ciepła:

+Q — gdy doprowadzamy ciepło do układu;

-Q — gdy odprowadzamy ciepło z układu do otoczenia;

+W — gdy wykonujemy nad układem pracę;

-W — gdy praca jest wykonywana przez układ.

GAZ DOSKONAŁY A GAZ RZECZYWISTY

Gazem doskonałym, nie mającym idealnego odzwierciedlenia w rzeczywistości, nazywamy teoretyczny model gazu o dwóch podstawowych własnościach:

1. między cząsteczkami gazu nie zachodzą żadne oddziaływania, z wyjątkiem tzw. zderzeń, czyli niezmiernie krótkotrwałych spotkań cząstek ze sobą lub ze ścianami naczynia, w którym gaz się znajduje.. Podczas tych zderzeń, traktowanych przez nas jako doskonale sprężyste, zachodzą zmiany pędu i energii cząsteczek gazu, zgodne z zasadami zachowania tych wielkości. Ruch cząsteczek gazu jest całkowicie chaotyczny. Droga przez nie zakreślana ma postać linii łamanej, złożonej z odcinków prostoliniowych, ponieważ zmiany kierunku ruchu zachodzą jedynie na skutek wyżej wspomnianych zderzeń.

2. cząsteczki gazu traktujemy jako punkty materialne, tzn. zaniedbujemy ich masę i objętość własną. Dzięki temu możemy przyjąć, że przestrzeń, w jakiej cząsteczki się poruszają, jest równa objętości zajmowanej przez gaz.

W warunkach rzeczywistych gaz doskonały nie istnieje, ponieważ: po pierwsze, nie ma cząsteczek nie posiadających masy i objętości; po drugie, w naturze nie zachodzą zderzenia doskonale sprężyste (część energii zawsze ulega rozproszeniu). Gazy rzeczywiste z większym lub mniejszym przybliżeniem podlegają jednak prawom ściśle słusznym dla gazu doskonałego, dlatego analizując ich własności fizyczne traktujemy je tak, jak gaz doskonały.

Główną cechą odróżniającą gazy rzeczywiste od gazu doskonałego jest występowanie oddziaływań międzycząsteczkowych. Oddziaływania te mogą być dwojakiego rodzaju — przyciągania lub odpychania. Gdy odległości między środkami cząsteczek przekraczają wartość ok. 2-10·10^-10 m, cząsteczki działają na siebie siłami przyciągania, mającymi charakter elektrostatyczny i zwanymi siłami van der Waalsa. Przy mniejszych odległościach pojawiają się siły odpychania, których wartość rośnie bardzo szybko wraz ze zmniejszaniem się odległości między cząsteczkami.

Siły van der Waalsa możemy podzielić na orientacyjne (powstałe w wyniku wzajemnych oddziaływań trwałych cząsteczek dipolowych), indukcyjne (działające na cząsteczki, które łatwo polaryzują się pod wpływem pól innych cząsteczek lub zewnętrznego pola elektrycznego, czyli tzw. dipole indukowane) i dyspersyjne (powstałe między dipolami chwilowymi, czyli trwającymi niezmiernie krótko asymetrycznymi stanami normalnie obojętnych elektrycznie drobin, powstałymi w wyniku nieustannego chaotycznego ruchu elektronów w tych drobinach). Każdy z tych trzech rodzajów sił wykazuje oczywiście zależność od odległości r między cząsteczkami — w dokładnym ujęciu wartość siły przyciągania jest proporcjonalna do r^-7.

Siły odpychania wynikają z odkształcenia powłok elektronowych oddziałujących cząsteczek. Najczęściej przyjmuje się, że są one proporcjonalne do r^--13.

Rzecz jasna, w przypadku każdej wyodrębnionej pary cząsteczek istnieje taka odległość r₀, dla której ich wzajemny układ jest maksymalnie stabilny — jest to tzw. położenie równowagi tych cząsteczek.

RÓWNANIA OPISUJĄCE STAN GAZU

Stan gazu opisują trzy parametry: objętość (V), ciśnienie (p) i temperatura (T). Każdy z tych trzech parametrów może mieć określoną wartość — w zależności od tego, który z nich przyjmiemy za stały, wyróżniamy trzy prawa opisujące stan gazu:

1. Prawo Boyle'a - Mariotte'a, rządzące przemianą izotermiczną (taką, w której wielkością stałą jest temperatura gazu, czyli nie zachodzi zmiana jego energii wewnętrznej): podczas izotermicznej przemiany stałej masy gazu ciśnienie jest odwrotnie proporcjonalne do objętości.

Ilustracją prawa Boyle'a - Mariotte'a w układzie osi p, V jest hiperbola.

2. Prawo Charlesa, rządzące przemianą izochoryczną (taką, w której wielkością stałą jest objętość gazu, czyli że nie mamy do czynienia z pracą wykonaną przez gaz lub nad nim): podczas izochorycznej przemiany stałej masy gazu ciśnienie jest wprost proporcjonalne do temperatury w skali bezwzględnej (skali Kelvina).

Ilustracją prawa Charlesa w układzie osi p, T jest prosta.

3. Prawo Gay-Lussaca, rządzące przemianą izobaryczną (taką, w której wielkością stałą jest ciśnienie, pod jakim gaz się znajduje): podczas izobarycznej przemiany stałej masy gazu jego objętość jest wprost proporcjonalna do temperatury w skali bezwzględnej (skali Kelvina).

Ilustracją prawa Gay-Lussaca w układzie osi V, T jest prosta.

RÓWNANIE CLAPEYRONA

Wszystkie trzy parametry (p, V, T) łączy prawo zilustrowane równaniem stanu gazu doskonałego:

Po uwzględnieniu ilości moli gazu i obliczeniu wartości stałej const otrzymujemy końcową postać prawa, ilustrowaną tzw. równaniem Clapeyrona:

pV = nRT

gdzie R jest obliczoną wartością stałej const, zwaną uniwersalną stałą gazową i mającą wartość:

PRZEMIANY GAZU DOSKONAŁEGO

Przemiany gazu doskonałego możemy pogrupować, przyjmując za kryterium ten parametr stanu gazu, który w danej przemianie pozostaje stały. Jak opisują prawa Boyle'a - Mariotte'a, Charlesa i Gay-Lussaca, stałymi parametrami mogą być temperatura, objętość albo ciśnienie — mamy wówczas do czynienia z odpowiednimi przemianami: izotermiczną, izochoryczną lub izobaryczną. Może również zdarzyć się, że przemianie będą ulegały wszystkie parametry stanu gazu przy równoczesnym braku wymiany ciepła z otoczeniem — taką przemianę nazwiemy adiabatyczną.

1. Przemiana izotermiczna. Jak wiadomo, podczas tej przemiany temperatura gazu pozostaje stała, czyli nie ulega zmianie jego energia wewnętrzna. Jak wynika z pierwszej zasady termodynamiki, jeżeli U = const, to ∆U = 0, a zatem ∆Q + ∆W = 0. Wartości ciepła i pracy doprowadzonych lub odprowadzonych z układu są zatem równe co do wartości bezwzględnych, lecz ich znaki są przeciwne.

Innymi słowy — jeżeli w przemianie izotermicznej dostarczamy gazowi ciepło, wykonuje on pracę (zwiększa się jego objętość). Wartości tego ciepła i pracy są sobie równe, lecz mają przeciwne znaki (ciepło ma znak + , ponieważ dostarczamy je do układu, a praca znak - , gdyż jest wykonywana przez układ nad otoczeniem). Jeżeli odbierzemy gazowi ciepło, jego objętość zmaleje zgodnie z prawem Boyle'a - Mariotte'a — mamy zatem do czynienia z sytuacją odwrotną.

2. Przemiana izochoryczna. W tej przemianie nie ulega zmianie objętość gazu, nie wykonuje on więc pracy. Podczas tej przemiany zachodzi zmiana energii wewnętrznej gazu — dostarczone ciepło nie ma szans zmienić się na pracę, zatem efektem jego doprowadzenia do układu staje się wzrost temperatury. Pierwsza zasada termodynamiki dla tej przemiany ma postać ∆U = ∆Q, gdzie ∆Q oznacza ciepło doprowadzone do gazu przy zachowaniu przezeń stałej objętości.

3. Przemiana izobaryczna. W przemianie tej po dostarczeniu ciepła Q przy zachowaniu stałego ciśnienia zachodzi zmiana objętości gazu. Mamy zatem do czynienia zarówno ze zmianą energii wewnętrznej, jak i z wykonaniem przez gaz pracy. Załóżmy, że dostarczamy do układu ciepło — zapis pierwszej zasady termodynamiki przyjmuje wówczas postać ∆U = ∆Q - ∆W (ponieważ gaz, zwiększając objętość zgodnie z prawem Gay-Lussaca, wykonuje pracę nad otoczeniem). Gdybyśmy odbierali układowi ciepło, znaki rozpatrywanych wielkości zmieniłyby się na przeciwne (objętość gazu zmalałaby, a zatem siły zewnętrzne wykonywałyby nad nim pracę).

Wartość wykonanej przez gaz pracy możemy obliczyć, posługując się wzorem:

∆W = p · ∆V

Otrzymujemy go, przekształcając prawidłowości:

∆W = F · ∆h;

F = p · S;

∆V = S · ∆h.

4. Przemiana adiabatyczna. Z tym rodzajem przemiany mamy do czynienia, gdy gaz nie wymienia ciepła z otoczeniem. W tej przemianie ulegają wszystkie (oczywiście z wyjątkiem masy) parametry stanu gazu. Gaz wykonuje pracę (jego objętość rośnie lub maleje), a zarazem ulega zmianie jego energia wewnętrzna (zmienia się wartość temperatury). Wiemy jednak, że między układem a otoczeniem nie zaszła wymiana ciepła, co pozwala zapisać dla tej przemiany I zasadę termodynamiki w następujący sposób: ∆U = ∆W (ponieważ ∆Q = 0).

Przykładem takiej przemiany może być rozprężanie gazu w izolacji cieplnej od otoczenia. Zmniejszenie ciśnienia powoduje automatyczny wzrost objętości gazu (gaz wykonuje pracę). Ponieważ wartość tej pracy nie może zostać zrównoważona wartością ciepła pobranego z otoczenia, cały proces odbywa się kosztem energii wewnętrznej układu, co objawia się spadkiem temperatury gazu.

PRACA WYKONANA PRZEZ GAZ I NAD GAZEM W PRZEMIANACH TERMODYNAMICZNYCH

Jak pamiętamy, wartość pracy wykonywanej przez gaz w przemianie izobarycznej jest najłatwiejsza do obliczenia, ponieważ przemiana ta zachodzi pod stałym ciśnieniem, a zatem działająca na gaz siła zewnętrzna ma stałą wartość.

Wartość pracy wykonanej w przemianach izotermicznej i adiabatycznej jest znacznie trudniejsza do obliczenia. Możemy jednak przyjąć zasadę, że liczbowa wartość pracy wykonanej przez gaz podczas przemiany termodynamicznej równa jest polu powierzchni zawartemu pod wykresem zależności p = f(V).

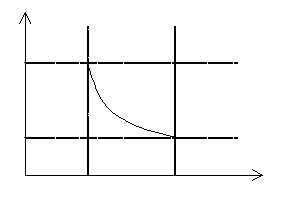
Należy pamiętać, że podczas przemiany izochorycznej gaz nie wykonuje pracy, ponieważ nie zachodzi żadna zmiana jego objętości!

CYKLE TERMODYNAMICZNE

Stałą masę gazu możemy poddać szeregowi takich przemian termodynamicznych, które po kilku zmianach jego parametrów doprowadzą go z powrotem do stanu początkowego. Taki szereg przemian nazywamy cyklem (obiegiem) termodynamicznym zamkniętym. Może się on składać z dowolnej ilości przemian termodynamicznych, muszą one jednak zachodzić w takiej kolejności i w taki sposób, aby w ich wyniku parametry gazu powróciły do swoich wstępnych wartości. Wykres takiego cyklu jest linią zamkniętą.

Wypadkowa praca gazu wykonana w trakcie całego cyklu termodynamicznego równa jest co do wartości polu powierzchni zawartemu wewnątrz tej linii zamkniętej.

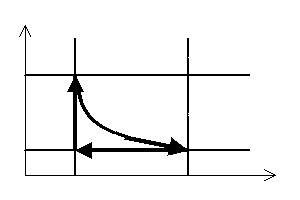
II ZASADA TERMODYNAMIKI

II zasada termodynamiki sformułowana została w oparciu o pojęcie silnika cieplnego, czyli mechanizmu pozwalającego na przekształcanie ciepła w pracę użyteczną podczas zachodzenia zamkniętego cyklu termodynamicznego.

Działanie silnika cieplnego można wyjaśnić następująco: w zamkniętym cyklu termodynamicznym część ciepła dostarczonego do układu zostaje przetworzona na pracę, ale część — jest to warunek konieczny, aby cykl mógł się zamknąć — musi z powrotem zostać oddana do otoczenia. W przypadku silnika źródło ciepła (część otoczenia dostarczającą ciepło) nazywamy grzejnicą, zaś tę część otoczenia, do której ciepło jest oddawane — chłodnicą.

Z warunków działania silnika cieplnego wynika postać II zasady termodynamiki:

Nie może istnieć silnik cieplny o sprawności μ = 1 = 100%, tzn. taki, który całe pobrane ciepło zamieniałby na pracę (nie oddawałby ciepła do chłodnicy).

Inne sformułowanie tej zasady mówi, że ciepło nie może samorzutnie przepływać z ciała zimniejszego do cieplejszego.

II zasada termodynamiki jest jedną z najważniejszych zasad współczesnej nauki. Dotyczy ona nie tylko silników cieplnych; ma charakter powszechny, gdyż mówi o kierunku rozchodzenia się i przepływu energii we Wszechświecie.

ZJAWISKA ZWIĄZANE Z PRZEPŁYWEM CIEPŁA

POJEMNOŚĆ CIEPLNA UKŁADU

Pojemnością cieplną q układu lub ciała nazywamy stosunek dostarczonej mu ilości ciepła do uzyskanego w ten sposób przyrostu temperatury.

Pojemność cieplna zależy od masy ciała, jego rodzaju, stanu skupienia oraz od przedziału temperatur, w którym nastąpiło ogrzanie ciała o ∆T i od sposobu ogrzewania.

CIEPŁO WŁAŚCIWE I MOLOWE

Ciepłem właściwym c w fachowym ujęciu nazywamy pojemność cieplną jednostki masy. Mówiąc prościej, jest to ilość energii potrzebna do zwiększenia temperatury jednostki masy substancji (najczęściej 1 kg) o jeden stopień (1˚K).

Ciepło właściwe dla każdej substancji może mieć inną wartość; wartości te dla różnych substancji są bardzo rozbieżne. Stosunkowo niewysokimi wartościami ciepła właściwego charakteryzują się metale (przy czym dla metali ciężkich jest ono znacznie mniejsze niż metali lekkich).

Ciepłem molowym C nazywamy z kolei pojemność cieplną jednostki liczności materii. Mówiąc prościej, jest to ilość energii potrzebna do zwiększenia temperatury jednostki liczności materii (najczęściej 1 mola) o jeden stopień (1˚K).

gdzie n jest liczbą moli danej substancji

Ponieważ liczbę moli substancji n możemy obliczyć ze wzoru

(gdzie M oznacza masę molową substancji),

uzyskujemy wzór na wzajemną zależność ciepła właściwego i molowego w postaci:

C = c · M.

Co ciekawe, ciepło molowe ciał stałych dla wszystkich substancji ma podobną wartość (ok. 24,5 do 25,5
). W przypadku gazów jego wartość zależy od ilości atomów w cząsteczce — dla gazów o cząsteczkach jednoatomowych wynosi mniej więcej
, dla gazów o cząsteczkach dwuatomowych ok.
, wreszcie dla gazów o cząsteczkach trójatomowych — ok.
. W praktyce możemy posługiwać się wszystkimi powyższymi wartościami jako przybliżonymi.

W przypadku cieczy zależności te nie są tak regularne i znacznie bardziej skomplikowane.

Warto wspomnieć, że ciepło właściwe substancji zależy od tego, czy ogrzewamy je w warunkach izochorycznych (c_v), czy izobarycznych (c_p). Dla ciał stałych i cieczy różnica między c_v i c_p jest niewielka, rzędu 2-4% wartości mierzonej, dla gazów natomiast staje się bardzo istotna.

Wiemy, że ciepło właściwe gazu w przemianie izobarycznej jest większe niż w przemianie izochorycznej (ponieważ dostarczana energia cieplna jest zużywana nie tylko na wzrost temperatury, ale również na pracę objętościową).

Porównując z kolei wartości ciepła molowego dla obu przemian otrzymujemy zależność:

C_p = C_v + R.

BILANS CIEPLNY

Bilans cieplny dotyczy zjawisk przekazywania energii na sposób ciepła pomiędzy ciałami. Opisuje się go prostym równaniem:

Q_pobr = Q_odd,

czyli ciepło pobrane przez jedno ciało układu równe jest ciepłu oddanemu mu przez drugie ciało lub przez otoczenie układu.

Zależnie od tego, jaki proces chcemy opisać, korzystamy z następujących wzorów:

1. Q = m · c_w · ∆T

gdzie m jest masą substancji poddanej przemianie,

c_w — wartością ciepła właściwego substancji

∆T — wartością zmiany temperatury.

Z tego wzoru korzystamy, gdy mamy do czynienia ze zmianą temperatury danej substancji po dostarczeniu lub odebraniu jej pewnej ilości ciepła.

2. Q = m · c_t

Q = m · c_w

Q = m · c_s

gdzie m jest masą substancji poddanej przemianie,

c_t , c_w i c_s — wartościami ciepła topnienia, wrzenia lub sublimacji substancji.

Z tego wzoru korzystamy, gdy dostarczenie szukanej ilości ciepła powoduje przemianę fazową substancji (na drodze topnienia, krzepnięcia, parowania, kondensacji, sublimacji lub resublimacji, o których mowa jest niżej).

PRZEJŚCIA FAZOWE

DEFINICJA FAZY I PRZEMIANY FAZOWEJ

Fazą nazywamy część układu fizycznie jednorodną. Nie musi ona być jednorodna również pod względem chemicznym — np. woda z lodem są układem dwufazowym, ale nienasycony roztwór soli — jednofazowym, mimo że chemicznie składa się on z dwóch substancji. Różne fazy tej samej substancji to np. różne stany skupienia (stały, ciekły lub gazowy, w odpowiednich warunkach mogące przechodzić jeden w drugi) albo jej odmiany alotropowe. Przejście substancji z jednej fazy w inną nazywamy przemianą fazową.

Wyróżniamy przemiany (przejścia) fazowe pierwszego i drugiego rodzaju. Przejścia pierwszego rodzaju charakteryzuje skokowa zmiana energii wewnętrznej ciała i jego gęstości lub objętości — zmianom tym towarzyszy pobranie lub oddanie pewnej ilości energii w postaci ciepła, tzw. ciepła przemiany. Przykładami przejść pierwszego rodzaju mogą być: topnienia, parowanie, sublimacja i przemiany do nich odwrotne oraz wzajemne przemiany odmian alotropowych. Przemianom fazowym drugiego rodzaju nie towarzyszą skokowe zmiany energii wewnętrznej i gęstości. Przykładem takiej przemiany jest np. przejście ferromagnetyka w paramagnetyk.

PRZEMIANY FAZOWE PIERWSZEGO RODZAJU

W odpowiednich warunkach w przyrodzie mogą zachodzić następujące przemiany fazowe:

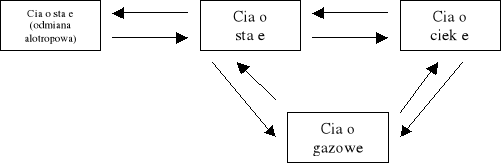
1. Przejścia ciało stałe — ciecz.

Wyróżniamy dwa rodzaje takiego przejścia: przejście ciała stałego w ciecz (bez zmiany temperatury), czyli topnienie (1), i przejście cieczy w ciało stałe, czyli krzepnięcie (2).

Ściśle określoną temperaturę topnienia i równą jej temperaturę krzepnięcia mają tylko substancje krystaliczne. Ciała stałe niekrystaliczne (szkło, twarde żywice, tworzywa sztuczne) nie mają określonej temperatury topnienia i przy podwyższonej temperaturze stopniowo miękną, łagodnie przechodząc w stan cieczy — początkowo bardzo lepkiej, w wyższych temperaturach o lepkości stopniowo malejącej.

W temperaturze idealnie równej temperaturze topnienia fazy ciekła i stała istnieją we wzajemnej równowadze dynamicznej (w każdej chwili tyle samo cząsteczek przechodzi z fazy stałej w ciekłą, co z ciekłej w stałą).

Ilość ciepła pobrana przez układ podczas topnienia jest proporcjonalna do masy stopionej substancji. Odpowiedni współczynnik, zwany krótko ciepłem topnienia, jest liczbowo równy ilości energii, jaką należy dostarczyć 1 kg substancji, aby przekształcić ją ze stanu ciekłego w stan stały bez zmiany temperatury. Rzecz jasna, ta sama ilość energii, jaką ciało pobiera podczas topnienia, jest przez nie oddawana podczas krzepnięcia.

Ciepło topnienia zużywane jest na zmianę energii wewnętrznej układu. Ponieważ temperatura w tym procesie pozostaje stała, więc i średnia energia kinetyczna cząsteczek pozostaje stała. Zmiana energii wewnętrznej polega zatem na wzroście energii potencjalnej cząsteczek. Na skutek tego osłabieniu ulegają siły wzajemnego oddziaływania cząsteczek i wzrastają ich wzajemne odległości.

Oprócz tego część ciepła topnienia zużywana jest na wykonanie pracy związanej ze zmianą objętości określonej masy ciała przy przejściu do innego stanu skupienia. Jeżeli topnienie zachodzi pod niewielkim ciśnieniem, ta część ciepła staje się zaniedbywalnie mała, ponieważ zmiany objętości są bardzo nieznaczne.

Ogólnie ciepło topnienia określonej substancji wyraża się wzorem:

gdzie U oznacza energię wewnętrzną jednostki masy danej substancji,

p jest ciśnieniem zewnętrznym,

a V — objętością danej masy substancji w stanie ciekłym lub stałym.

Jednostką ciepła topnienia (podobnie zresztą jak w przypadku innych przemian fazowych) jest J/kg.

UWAGA: niektóre substancje (najprostszym przykładem jest woda) przy przejściu ze stanu stałego w ciekły nie zwiększają swej objętości, lecz zmniejszają ją. W takim przypadku należy we wzorze zamienić objętości miejscami.

Proces krzepnięcia również ma swoją osobliwość. Jeżeli bardzo powoli oziębiać wysoko oczyszczoną ciecz, można przekroczyć temperaturę krzepnięcia, a ciało nie zmieni stanu skupienia. Ciecz, której temperatura jest niższa od temperatury krzepnięcia, nazywamy cieczą przechłodzoną. Jest to stan nietrwały. Każde zaburzenie, np. w postaci drobnego zanieczyszczenia wrzuconego do cieczy albo nawet potrząśnięcia naczyniem, które ją zawiera, powoduje jej gwałtowne krzepnięcie. Wyjątkami są ciecze o dużej lepkości — stan przechłodzenia może być dla nich stanem trwałym. Jest to powód, dla którego niektóre ciała bezpostaciowe możemy traktować jako przechłodzone ciecze o skrajnie wysokiej lepkości.

2. Przejścia ciecz — ciało lotne.

Przemian fazy ciekłej w lotną odbywa się na drodze parowania (3), gdy przemieniamy ciało ciekłe w lotne, lub skraplanie, inaczej kondensacja (4) — gdy ciało lotne przemienia się w ciecz.

Parowanie jest interesującym przypadkiem przemiany fazowej, ponieważ nie zachodzi w określonej temperaturze, a w całym przedziale temperatur między temp. topnienia a temp. wrzenia. Ciepło parowania jest liczbowo równe ilości energii, którą należy dostarczyć 1 kg cieczy, aby przeszła a stan pary w danej temperaturze (oczywiście najczęściej bierze się pod uwagę temperaturę wrzenia). Ciepło parowania jest funkcją temperatury — maleje stopniowo z jej wzrostem, a w temperaturze krytycznej (o której mowa niżej) równa się zeru.

Prędkość parowania w danej temperaturze w przybliżeniu określa zależność:

gdzie M jest masą cieczy, która przeszła w stan pary;

S — powierzchnią swobodną cieczy;

p_n — ciśnieniem pary nasyconej w danej temperaturze;

p — ciśnieniem pary cieczy nad jej powierzchnią swobodną;

p₀ — ciśnieniem atmosferycznym;

k — wartością stałą, zależną m.in. od rodzaju substancji.

Z powyższego wzoru wynika, że im mniejsze jest ciśnienie pary nad cieczą (p), tym większa szybkość parowania. Dlatego w praktyce, aby zwiększyć szybkość parowania, usuwamy parę z sąsiedztwa przedmiotów suszonych (dzieje się tak np. przy suszeniu prania na wietrze). Również zmniejszenie ciśnienia zewnętrznego p₀ powoduje przyspieszenie parowania — dlatego też w przemyśle wodę z mleka, przypraw, grzybów itd. odparowuje się próżniowo.

Proces parowania polega na przechodzeniu poszczególnych cząsteczek cieczy poza jej obręb — cząsteczki muszą zatem osiągać tak dużą energię kinetyczną, aby wystarczyła ona na wykonanie pracy przeciw siłom spójności. Ze wzrostem temperatury średnia energia kinetyczna cząsteczek wzrasta i coraz więcej cząsteczek osiąga na tyle dużą jej wartość, aby pokonać siły spójności i oderwać się od powierzchni cieczy — stąd też podwyższenie temperatury pociąga za sobą wzrost szybkości procesu parowania. Cząsteczki przechodzące w stan pary unoszą jednak ze sobą część energii, co przekłada się na spadek temperatury cieczy parującej. Odwrotna sytuacja towarzyszy skraplaniu — średnia energia kinetyczna cząsteczek maleje, przechodzą one zatem z pary do cieczy, czemu towarzyszy wzrost jej temperatury.

Jak wspomniano już na początku, procesy parowania i skraplania zachodzą nieprzerwanie w całym przedziale temperatur (od krzepnięcia do wrzenia). O tym, czy ciecz paruje, czy skrapla się, decyduje stan równowagi dynamicznej między fazami. Jeżeli w jednostce czasu więcej cząsteczek przechodzi ze stanu lotnego w ciekły, mówimy o skraplaniu lub kondensacji cieczy; jeżeli więcej cząsteczek przechodzi ze stanu ciekłego w lotny — mówimy, że ciecz paruje. Para znajdująca się nad cieczą w tym drugim przypadku nosi nazwę pary nienasyconej.

Kiedy między cieczą a parą w danej temperaturze wytworzy się stan równowagi dynamicznej (w przybliżeniu tyle samo cząsteczek w jednostce czasu opuszcza ciecz i do niej powraca), mówimy, że nad powierzchnią swobodną znajduje się para nasycona.

Wrzenie jest szczególnym przypadkiem parowania — zachodzi ono intensywnie nie tylko na powierzchni swobodnej, ale w całej objętości cieczy, w określonej i charakterystycznej dla każdej substancji temperaturze, zwanej temperaturą wrzenia. Aby proces wrzenia mógł nastąpić, w cieczy muszą znajdować się tzw. zarodzie — mikroskopijne pęcherzyki gazów na dnie i ściankach naczynia, w szczelinkach i porach, a w naczyniach gładkich — w tych miejscach, których ciecz nie zwilża. Wynika z tego, że ciecz doskonale czysta, doskonale odgazowana i doskonale zwilżająca naczynie wrzeć nie powinna. Oczywiście w praktyce jest to przypadek niemożliwy do zrealizowania. Możemy jednak podgrzać ciecz pod normalnym ciśnieniem do temperatury wyższej od temperatury wrzenia bez doprowadzenia do tego procesu — nazywamy ją wówczas cieczą przegrzaną. Podobnie jak w przypadku cieczy przechłodzonej, jej stan jest nietrwały i najdrobniejsze nawet zakłócenie może spowodować gwałtowane, nieraz wybuchowe wrzenie i uwalniania się dużych ilości pary.

Podczas wrzenia temperatura cieczy nie wzrasta — dostarczane ciepło zużywane jest na zmianę energii cząsteczek cieczy (przezwyciężenie łączących je sił spójności) oraz na pracę związaną ze wzrostem objętości pary w porównaniu z objętością cieczy i pokonywaniem ciśnienia zewnętrznego działającego na rozszerzające się pęcherzyki pary.

3. Przejścia ciało stałe — ciało lotne.

Przejścia takie zachodzą rzadko i dotyczą tylko niektórych substancji (np. naftalenu). Dotyczą one bezpośredniego przechodzenia cząsteczek z ciała stałego w otaczającą przestrzeń, czyli ze stanu stałego w lotny z ominięciem fazy ciekłej — jest to sublimacja (5). Procesem odwrotnym jest resublimacja (6). Ciepło sublimacji Q_s jest równe sumie ciepła topnienia Q_t i ciepła parowania Q_p. Sublimacja i resublimacja zachodzą w każdej temperaturze i dotyczą wyłącznie powierzchni ciała.

4. Przejścia alotropowe.

Przemiany alotropowe dotyczą zmian struktury wewnętrznej danego ciała, np. przechodzenia diamentu w grafit i grafitu w diament. Nie są to zależności tak proste, jak w przypadku topnienia i krzepnięcia lub wrzenia i parowania — zazwyczaj odwrotnie do siebie przemiany alotropowe zachodzą w bardzo różnych warunkach ciśnienia i temperatury, często w obecności. Aby przemienić wspomniany diament w grafit, wystarczy ogrzać go bez dostępu powietrza do temp. około 1500˚C. Przemiana odwrotna, czyli grafitu w diament, wymaga zastosowania ogromnego ciśnienia (rzędu 20 000 MPa) i temperatury około 4000˚C.

RÓWNOWAGA FAZ. PUNKT POTRÓJNY

Stan współistnienia dwóch faz danej substancji w równowadze jest możliwy tylko w określonych warunkach temperatury i ciśnienia. Każdy stan równowagi można przedstawić za pomocą punktu w układzie osi (T,p). Zbiór tych punktów tworzy krzywą równowagi faz, określającą zależność temperatury przemiany fazowej od ciśnienia. Jeżeli krzywe obrazujące równowagę faz: stałej i ciekłej, ciekłej i lotnej, lotnej i stałej — umieścimy na jednym wykresie, okaże się, że wszystkie one spotykają się w jednym punkcie, zwanym punktem potrójnym — jest to punkt równowagi trzech faz, określany dla dane substancji charakterystycznymi wartościami temperatury T₀ i ciśnienia p₀.

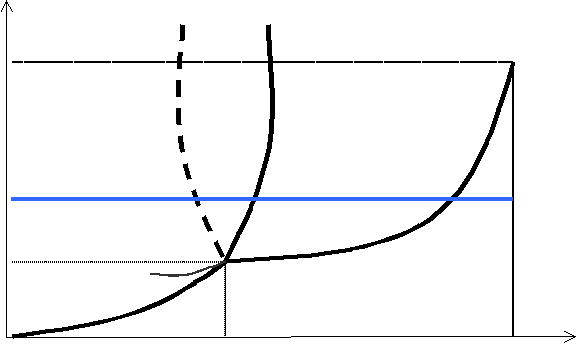
Powyższy wykres nosi nazwę DIAGRAMU FAZOWEGO. Określa on położenia punktów równowagi między poszczególnymi fazami danej substancji. Pogrubione linie ograniczają pewne obszary wykresu — wartościom temperatury i ciśnienia zawartym między tymi liniami odpowiada dany stan skupienia. Samym granicom, oznaczonym liniami, odpowiada stan równowagi między ciałem stałym lub cieczą a parą nasyconą. Krótka, cienka linia zachodząca w obszar ciała stałego odpowiada cieczy przechłodzonej.

Wątpliwości mogą budzić dwie granice między obszarem ciała stałego i cieczy (linie ciągła i przerywana, będące swoimi lustrzanymi odbiciami). Ich pojawienie się wyjaśnia zależność Clausiusa - Clapeyrona:

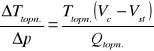
Określa ona stosunek zmiany temperatury topnienia do określonej zmiany ciśnienia. Wynika z niej, że dla ciał, których objętość w stanie stałym jest większa niż w stanie ciekłym (była o nich mowa już we wzorze na ciepło topnienia), wzrost ciśnienia powoduje zmniejszanie się temperatury przemiany fazowej. Przejście fazy stałej w ciekłą dla tych ciał przedstawia linia przerywana. Wszystkie pozostałe ciała we wszystkich pozostałych przemianach charakteryzują się wzrostem temperatury przemiany wraz ze wzrostem ciśnienia, ponieważ przejścia ciało stałe — ciecz, ciało stałe — gaz i ciecz — gaz charakteryzują się dla nich wzrostem objętości.

Dwa charakterystyczne punkty diagramu fazowego, zaznaczone kolorem czerwonym, to punkt O, czyli punkt potrójny, i punkt K, czyli tzw. punkt krytyczny. Początek układu współrzędnych jest trzecim punktem charakterystycznym, odpowiadającym temperaturze zera bezwzględnego i zerowemu ciśnieniu pary.

Prosta charakterystyka punktu potrójnego została już przedstawiona. Warto jeszcze dodać, że jednym punktem potrójnym charakteryzują się najprostsze diagramy fazowe — tzn. takie, które przedstawiają substancję mającą tylko jedną odmianę fazy stałej. Dla substancji mającej więcej niż jedną fazę stałą (odmiany alotropowe) liczba punktów potrójnych zwiększa się i sytuacja ogromnie się komplikuje.

Podwójna błękitna linia na wykresie przedstawia przejścia fazowe substancji przy stałym ciśnieniu (warunki standardowe), a zwiększającej się wartości temperatury. Widać, że w przypadku, gdy parametry punktu potrójnego przypadają znacznie poniżej warunków standardowych, substancja występuje w trzech stanach skupienia. W przypadku, gdy punkt potrójny znajduje się powyżej wartości odpowiadających tym warunkom, substancja przechodzi ze stanu stałego bezpośrednio w stan lotny (błękitna linia nie przecina obszaru stanu ciekłego).

Warto zapamiętać parametry punktu potrójnego wody, o T₀ = 273,16˚K i p₀ = 613 Pa.

Jeżeli chodzi o punkt krytyczny, odnosi się on do stanu substancji poddanej wysokiemu ciśnieniu i temperaturze.

Jak wiadomo, zwiększanie ciśnienia powoduje wzrost temperatury koniecznej, aby mogła zajść przemiana fazowa ciecz — ciało lotne. Zwiększając odpowiednio ciśnienie, otrzymujemy ciecze przegrzane. Dla każdej substancji istnieje jednak taka temperatura, zwana temperaturą krytyczną (T_k), dla której nawet anormalnie wysokie ciśnienie nie spowoduje utrzymania stanu cieczy. Powyżej wartości tej temperatury (oczywiście dla różnych substancji jest ona różna) każda substancja przechodzi w stan lotny. Dla jej określenia nie używamy już nazwy „para”, lecz „gaz”. Między parą a gazem nie zachodzi przemiana fazowa. Temperaturze krytycznej na diagramie fazowym odpowiada tzw. ciśnienie krytyczne (p_k).

Na koniec rozważań dotyczących przemian fazowych dodać można, że na temperaturę przemiany (topnienia, wrzenia, sublimacji) ma ogromny wpływ czystość substancji. Jak wiadomo, roztwory ciał stałych w cieczach mają temperatury wrzenia wyższe, a temperatury topnienia niższe od odpowiednich temperatur dla czystych rozpuszczalników. Wielkość tych zmian zależy od rodzaju rozpuszczalnika oraz od rodzaju i stężenia substancji rozpuszczonej.

WILGOTNOŚĆ POWIETRZA

DEFINICJA WILGOTNOŚCI POWIETRZA

Zawartość pary wodnej w powietrzu atmosferycznym ma ogromne znaczenie, zarówno dla kształtowania pogody i klimatu, jak i dla biosfery ziemi. Do scharakteryzowania zawartości pary wodnej w powietrzu służą trzy najczęściej używane wielkości:

• Prężność (ciśnienie cząstkowe, ciśnienie parcjalne) pary wodnej w powietrzu. Wyrażamy ją w paskalach (Pa).

• Wilgotność bezwzględna W₀ — określamy ją liczbowo jako masę pary wodnej zawartej w 1 m³ powietrza. Jej jednostką jest kg/m³.

• Wilgotność względna W, którą określamy jako stosunek aktualnej wilgotności bezwzględnej powietrza do wilgotności bezwzględnej odpowiadającej stanowi nasycenia powietrza parą wodną w tej samej temperaturze.

Wilgotność względną wyrażamy w procentach.

Wartość temperatury, w której powietrze staje się nasycone parą wodną, to jest gdy w danych warunkach wilgotność względna osiąga wartość 100%, nazywamy punktem rosy. Jeżeli temperatura powietrza o danej wilgotności bezwzględnej spadnie na tyle znacznie, że stężenie pary wodnej przekroczy poziom nasycenia, część tej pary — podobnie jak w krystalizującym roztworze — musi się „wytrącić” w postaci kropel wody. Na tym właśnie polega zjawisko pojawiania się rosy.

ZASADY POMIARU WILGOTNOŚCI POWIETRZA

Istnieje wiele metod pomiaru wilgotności powietrza. Najpopularniejsze między nimi są trzy poniżej omówione:

• Metoda psychometryczna.

Psychometr składa się zasadniczo z dwóch identycznych termometrów rtęciowych, z których jeden ma zbiorniczek owinięty stale wilgotnym materiałem. Woda, parując z materiału, pobiera z układu ciepło, wskutek czego obniża się temperatura termometru wilgotnego. Różnica wskazań obu termometrów zależy od prędkości parowania, ta zaś — od wilgotności względnej otaczającego powietrza i od jego temperatury. Gdy wilgotność względna wynosi 100%, obydwa termometry wskazują jednakową temperaturę.

Wilgotność powietrza znajdujemy ze wzoru psychometrycznego:

gdzie p oznacza wartość szukanego ciśnienia pary w powietrzu;

p_n jest ciśnieniem pary nasyconej w temperaturze wskazywanej przez termometr wilgotny;

α jest stałym współczynnikiem, zależnym od ruchu powietrza wokół termometru wilgotnego;

T_w — jest temperaturą wskazywaną przez termometr wilgotny;

T_s — jest temperaturą wskazywaną przez termometr suchy;

p₀ jest wartością ciśnienia atmosferycznego.

W praktyce najczęściej korzysta się z gotowych tablic, z których odczytujemy uzyskane wartości T_s i T_w i odpowiadającą im wartość wilgotności względnej.

• Metoda punktu rosy.

Metalowe naczynie o płaskiej, dobrze wypolerowanej od zewnątrz ściance bocznej oziębiamy przez intensywne parowanie eteru znajdującego się wewnątrz. Gdy temperatura eteru i naczynia (a wraz z nimi powietrza przylegającego do wypolerowanej ścianki naczynia) osiągnie punkt rosy, ścianka pokryje się mikroskopijnymi kroplami rosy i zmatowieje. W chwili pojawienia się tej mgiełki odczytujemy temperaturę na zanurzonym w naczyniu termometrze. Znając temperaturę punktu rosy i temperaturę powietrza, możemy za pomocą gotowych tablic określić wilgotność bezwzględną i względną.

• Metoda higrometryczna.

Polega ona na pomiarze zmiany długości odtłuszczonego włosa ludzkiego, zachodzącej pod wpływem zmian wilgotności powietrza. Długość włosa ludzkiego wzrasta bowiem wraz z wilgotnością względną. Zmiany długości włosa są przenoszone przez układ dźwigni na wskazówkę przesuwającą się wzdłuż skali wycechowanej od razu w % wilgotności względnej. Przyrząd taki nie jest zbyt dokładny i co pewien czas wymaga sprawdzenia. Jest jednak bardzo dogodny w użyciu. Korzystamy z niego przy konstrukcji higrografów, które służą do otrzymywania wykresu zmian wilgotności w czasie.

Znane są także inne metody pomiaru wilgotności, oparte na zmianie masy bibuły nasyconej chlorkiem wapnia, zmianie tonu napiętej struny, zmianie barwy powierzchni nasyconej roztworem chlorku kobaltowego itd.

20218/L → 2374505

---