ŁĄCZENIE KONDENSATORÓW

Kondensatory płaskie możemy łączyć szeregowo lub równolegle, w zależności od tego, czy chcemy otrzymać układ o pojemności zastępczej większej, czy mniejszej od pojemności kondensatorów łączonych.

1. Równoległe łączenie kondensatorów:

W takiego rodzaju połączeniu napięcie przyłożone do okładek każdego z kondensatorów jest jednakowe, a ładunek zgromadzony na ich okładkach zależy od ich pojemności:

Całkowity ładunek Q zgromadzony w układzie kondensatorów jest równy sumie ładunków na połączonych ze sobą okładkach o jednakowym potencjale:

Pojemność zastępcza układu kondensatorów połączonych równolegle wynosi zatem:

i jest większa od największej pojemności w układzie.

Jeżeli łączymy ze sobą n kondensatorów o jednakowej pojemności C, pojemność zastępcza będzie wynosiła:

2. Szeregowe łączenie kondensatorów:

Przy takim połączeniu całkowity ładunek na okładkach wszystkich kondensatorów jest jednakowy, a napięcie na nich zależy od ich pojemności.

Będzie ono równe sumie napięć na poszczególnych kondensatorach. Całkowity spadek potencjału na wszystkich kondensatorach wynosi zatem:

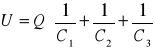
Z tego wynika wzór na pojemność zastępczą układu:

Pojemność ta jest zatem zawsze mniejsza od najmniejszej pojemności w układzie.

Jeżeli łączymy ze sobą szeregowo n kondensatorów o jednakowej pojemności C, pojemność zastępcza układu będzie wynosiła:

PRACA I MOC PRĄDU STAŁEGO

Moc P prądu stałego wydzielana na oporze R jest zdefiniowana wzorami:

Jednostką mocy jest wat (1 W):

Powyższe wzory dotyczą wyłącznie mocy wydzielanej na oporze w postaci ciepła.

Moc wydzielaną na całym obwodzie, złożonym z kilku oporów, obliczamy w oparciu o następujące prawidła:

• Stosunek mocy wydzielanych na oporach połączonych szeregowo jest równy stosunkowi tych oporów:

Największa moc wydziela się na oporze o największej wartości.

• Stosunek mocy wydzielanych na oporach połączonych równolegle jest równy stosunkowi odwrotności tych oporów:

Największa moc wydziela się na oporze o najmniejszej wartości.

Pracę prądu stałego o natężeniu I, napięciu U i czasie przepływu t obliczamy z iloczynu:

Jeżeli w obwodzie działa źródło siły elektromotorycznej, moc tego źródła dana jest wzorem:

Wzór ten wywodzimy z definicji SEM, która mówi, że siła elektromotoryczna jest liczbowo równa pracy, jaką źródło wykonuje przeciw siłom pola elektrycznego, przenosząc ładunek 1 C z bieguna o potencjale niższym do bieguna o potencjale wyższym:

.

Moc wydzielaną na oporze w takim obwodzie wyznaczamy natomiast z zależności:

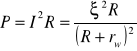
gdzie ξ oznacza SEM źródła prądu,

R — wartość oporu, na którym wydziela się moc,

a r_w — opór wewnętrzny źródła prądu.

PRĄD ELEKTRYCZNY I ELEKTROCHEMIA

DYSOCJACJA ELEKTROLITYCZNA

Dysocjacja elektrolityczna zachodzi, kiedy rozpuszczamy w wodzie związki o budowie jonowej. Zjawisko to oznacza rozpad cząsteczki na jonu lub uwalnianie jonów z sieci kryształu pod wpływem dipolowych cząsteczek wody.

ELEKTROLIZA

Elektrolizą nazywamy proces przepływu prądu stałego (przyłożonego z zewnątrz) przez elektrolity wraz z reakcjami chemicznymi, które towarzyszą temu przepływowi.

Układ, w którym przeprowadzamy elektrolizę, nosi nazwę elektrolizera. Elektrodę podłączoną do dodatniego bieguna źródła prądu nazywamy anodą, elektrodę ujemną — katodą. W wyniku przepływu prądu w elektrolicie zachodzą reakcje utleniania i redukcji, przy czym utlenianie zachodzi zawsze na anodzie, redukcja zaś — na katodzie.

Na katodzie w pierwszej kolejności rozładowują się kationy metali ciężkich, czyli metali położonych w szeregu napięciowym na prawo od glinu.

Jeżeli roztwór nie zawiera jonów takich metali, na katodzie wydziela się wodór pochodzący z rozładowania kationów H⁺ (jeżeli odczyn roztworu jest kwaśny)

lub redukcji cząsteczek wody (jeżeli roztwór ma odczyn zasadowy lub obojętny).

Na anodzie w pierwszej kolejności rozładowują się aniony kwasów beztlenowych, np. Cl^-. Jeżeli są one nieobecne w roztworze, na anodzie wydziela się tlen pochodzący z rozładowania jonów OH^- (w roztworach zasadowych):

lub utleniania cząsteczek wody (jeżeli roztwór jest kwaśny lub obojętny):

Jeżeli anoda nie jest wykonana z metalu szlachetnego lub grafitu, jej materiał może również ulegać roztwarzaniu:

PRAWA FARADAYA

Stwierdzono, że masa m substancji wydzielonej na którejkolwiek z elektrod podczas przepływu prądu przez elektrolit zależy od natężenia prądu I i czasu jego przepływu t.

Jest to treść pierwszego prawa elektrolizy Faradaya, które mówi, że masa substancji wydzielonej na elektrodzie jest wprost proporcjonalna do natężenia prądu płynącego przez elektrolit i od czasu trwania elektrolizy.

Współczynnik proporcjonalności k z powyższego równania jest wielkością stałą i charakterystyczną dla danej substancji wydzielanej na elektrodzie. Wielkość tę nazywamy równoważnikiem elektrochemicznym tej substancji.

Równoważnik ten informuje nas, ile wynosi masa substancji wydzielonej na elektrodzie podczas przepływu prądu o natężeniu 1 A trwającego 1 sekundę (innymi słowy — po przepłynięciu lub ładunku 1 C).

Czasami jako jednostkę równoważnika elektrochemicznego stosuje się
lub nawet
ponieważ przepływ ładunku 1 C powoduje wydzielanie się na elektrodzie bardzo niewielkich ilości substancji.

II PRAWO FARADAYA

Jak się okazuje, równoważnik elektrochemiczny k substancji zależy jej masy molowej M i od ładunku jonów tej substancji, będącego iloczynem we:

gdzie N_A oznacza liczbę Avogadra (6,02 · 10²³),

w jest wartościowością jonu,

a e — ładunkiem elementarnym (1,6 · 10^-19 C).

Jak widać, spomiędzy wyrażających go wielkości dwie (N_A i e) są stałe. Iloczyn tych wielkości również musi być stały. Nazywamy go stałą Faradaya F. Wartość tej stałej jest równa ładunkowi N_A, czyli 1 mola elektronów. W przeliczeniu na kulomby daje to około 96 500 C.

Wartość stałej Faradaya wynosi zatem

Używając tej stałej, możemy zapisać wzór na równoważnik elektrochemiczny w prostszej postaci:

Zapis ten wyraża drugie prawo elektrolizy Faradaya.

Sens fizyczny stałej Faradaya jest następujący: podczas przepływu przez elektrolit ładunku określanego przez tę stałą (czyli 96 500 C) na każdej z elektrod wydziela się ilość moli substancji równa
— czyli, inaczej mówiąc, masa substancji równa
.

ELEKTROMAGNETYZM

INDUKCJA MAGNETYCZNA

Stwierdzone zostało, że pole magnetyczne działa pewną siłą na ładunki lub przewodniki z prądem umieszczone w jego obszarze. Siła ta nazywana jest siłą elektrodynamiczną, a jej wartość wynosi:

dla ładunku q poruszającego się z prędkością v pod kątem α do linii sił pola (tzw. siła Lorentza)

lub:

dla przewodnika o długości l, w którym płynie prąd o natężeniu I, ustawionego pod kątem α do linii sił pola.

Wielkość B występująca w obydwu powyższych wzorach jest charakterystyczna dla danego pola magnetycznego, a nazywana jest indukcją magnetyczną pola. Jest ona liczbowo równa wartości siły działającej na przewodnik o długości 1 m, w którym płynie prąd o natężeniu 1 A, ustawiony prostopadle do linii sił pola magnetycznego (α = 90˚, sin α = 1), lub na cząstkę o ładunku 1 C, poruszającą się prostopadle do linii sił pola z prędkością 1 m/s.

Jednostką indukcji magnetycznej jest tesla (1 T).

ZJAWISKO INDUKCJI ELEKTROMAGNETYCZNEJ

Na początku XIX w. Faraday stwierdził, że zmienny strumień magnetyczny przenikający przez obwód elektryczny wzbudza w nim przepływ prądu.

Spostrzeżenie to jest szczególnym przypadkiem zjawiska indukcji magnetycznej. Prąd płynący w przewodniku nazywamy prądem indukcyjnym. Wywołująca go różnica potencjałów (SEM indukcji) opisana jest wzorem:

gdzie ∆Ф oznacza zmianę strumienia magnetycznego przepływającego przez nieruchomy obwód elektryczny,

a ∆t — czas, w jakim zmiana ta się dokonała.

Ponieważ strumień magnetyczny przepływający przez daną powierzchnię umieszczoną w polu magnetycznym definiujemy jako:

gdzie S oznacza wielkość powierzchni,

B — wartość indukcji magnetycznej pola,

a α jest kątem pomiędzy powierzchnią a wektorem indukcji B,

zmiana strumienia może się łączyć albo ze zmianą indukcji pola (nieruchomy przewodnik umieszczony w zmiennym polu magnetycznym), albo ze zmianą powierzchni S (przewodnik przesuwający się przez stałe pole magnetyczne) czy kąta α (przewodnik obracający się w stałym polu magnetycznym).

Jeżeli zależność wielkości strumienia od czasu jest liniowa, możemy umieścić ją na wykresie. Jeśli czas t odłożymy na osi odciętych, a strumień Φ na osi rzędnych, to tangens kąta nachylenia wykresu względem osi odciętych (α) będzie równy wartości SEM indukcji.

Zjawisko wzbudzania prądu indukcyjnego, zwane zjawiskiem Faradaya, spowodowane jest działaniem siły elektrodynamicznej pola (siły Lorentza) na swobodne elektrony przewodnika. Pod wpływem tej siły zaczynają się one poruszać, co automatycznie wiąże się z przepływem prądu.

W przypadku, gdy przewodnik porusza się w polu magnetycznym, wzbudza się w nim stała SEM indukcji o wartości:

Znając wartość tej SEM, możemy obliczyć natężenie wzbudzanego prądu indukcyjnego, wynoszące:

gdzie R jest oporem przewodnika. Wartość natężenia zależy od bezwzględnej wartości SEM indukcji. Znak tej SEM określa kierunek przepływu prądu indukcyjnego. Zjawisko to precyzuje reguła Lenza, mówiąca, że prąd indukcyjny ma taki kierunek, że przeciwdziała zmianie, która go wywołała (jest to sens fizyczny znaku „-” we wzorze na SEM indukcji).

POLE MAGNETYCZNE WYTWARZANE PRZEZ PRZEWODNIK Z PRĄDEM

Zostało dowiedzione, że przewodnik, w którym płynie prąd elektryczny o stałym natężeniu, wytwarza wokół siebie pole magnetyczne o indukcji B obliczanej ze wzoru:

gdzie I oznacza natężenie prądu w przewodniku,

r jest odległością danego punktu pola od przewodnika,

a μ₀ — wielkością stałą, tzw. przenikalnością magnetyczną próżni (4π · 10^-7 N/A²).

Z kolei prąd o zmieniającym się w czasie natężeniu będzie powodował powstawanie pola o zmiennej indukcji. Pole to może oddziaływać na obwody elektryczne znajdujące się w jego zasięgu — zarówno na obwód, który je wytwarza, jak i na wszystkie pozostałe — powodując powstawanie w nich SEM indukcji.

INDUKCJA WZAJEMNA

Zjawisko indukcji wzajemnej zachodzi, gdy jeden obwód elektryczny znajdzie się w zmiennym polu magnetycznym wytwarzanym przez inny obwód.

Rozważmy dwa obwody elektryczne. Niech w pierwszym z nich płynie prąd elektryczny o określonym natężeniu. Strumień magnetyczny pola wytwarzanego przez ten prąd jest w każdej chwili proporcjonalny do natężenia prądu I.

Jeżeli natężenie prądu w obwodzie pierwszym jest stałe, strumień magnetyczny przepływający przez obwód drugi również jest stały. Jeżeli jednak natężenie prądu w obwodzie pierwszym zmienia się w czasie, zmianie ulega również strumień pola objęty przez drugi obwód. Powoduje to powstanie w drugim obwodzie SEM indukcji o wartości proporcjonalnej do zmiany strumienia (a zatem i do zmiany natężenia), a w konsekwencji — przepływ prądu w tym obwodzie.

Powstająca siła elektromotoryczna jest zatem proporcjonalna do zmiany natężenia prądu w czasie t. Wielkość M, będąca współczynnikiem proporcjonalności, nazwana została współczynnikiem indukcji wzajemnej. Jednostką współczynnika indukcji wzajemnej jest 1 henr (1 H). Indukcja wzajemna między dwoma obwodami ma wartość 1 H, jeżeli zmiana natężenia prądu w pierwszym obwodzie o 1 A w ciągu 1 s powoduje powstanie w drugim obwodzie SEM indukcji równej 1 V.

ZJAWISKO SAMOINDUKCJI

Jeżeli mamy do czynienia z obwodem, w którym płynie prąd o zmiennym natężeniu, to przepływ tego prądu spowoduje zmiany strumienia magnetycznego, przenikającego przez ten obwód. Jak wiemy, zmienny strumień magnetyczny jest źródłem SEM indukcji. Dodatkowa różnica potencjałów będzie zatem powstawała również w samym przewodniku, w którym płynie prąd o zmiennym natężeniu,. Zjawisko to nazywamy samoindukcją, a SEM wytwarzaną w obwodzie przez prąd o zmiennym natężeniu — SEM samoindukcji.

Wartość SEM samoindukcji wiąże się ze zmianą strumienia, a ta z kolei proporcjonalna jest do zmiany natężenia prądu. Zależność tę podaje wzór:

Współczynnik proporcjonalności L nosi nazwę współczynnika indukcyjności lub samoindukcji. Wartość jego zależy od „geometrii” (kształtu i wielkości) obwodu i właściwości magnetycznych środowiska, w którym obwód się znajduje. Jednostką indukcyjności, podobnie jak współczynnika indukcji wzajemnej, jest 1 henr (1 H). Jest to indukcyjność takiego obwodu, w którym zmiana natężenia prądu o 1 A w ciągu 1 s powoduje powstanie SEM samoindukcji równej 1 V.

Zjawisko samoindukcji wyjątkowo dobrze ilustruje nam regułę Lenza. Obserwujemy, że gdy natężenie prądu w obwodzie maleje (
< 0), to powstająca SEM indukcji ma znak dodatni, czyli wzbudza przepływ prądu o natężeniu mającym ten sam kierunek, co natężenie zanikające. Powoduje to chwilowe podtrzymanie przepływu prądu. Jeżeli natomiast natężenie rośnie (maleje (
> 0), SEM indukcji ma znak ujemny i powoduje przepływ prądu o natężeniu skierowanym przeciwnie. Innymi słowy, zwiększający się prąd jest częściowo tłumiony.

Zjawisko samoindukcji najczęściej obserwuje się w obwodzie zawierającym zwojnicę.

PRĄD PRZEMIENNY

WYTWARZANIE NAPIĘĆ SINUSOIDALNIE ZMIENNYCH

Jeżeli mamy do czynienia na przykład z ramką z przewodnika, obracającą się w polu magnetycznym dookoła swej osi geometrycznej z częstością kołową (prędkością kątową) ω, wartość SEM jest sinusoidalnie zmienna w czasie, ponieważ kąt ustawienia powierzchni w stosunku do linii sił pola nieustannie ulega zmianie.

Ponieważ kąt α proporcjonalny jest do czasu obrotu t (α = ωt), wzór ten możemy zapisać:

Jest ona zależna od prędkości kołowej (a więc od częstotliwości υ) obrotu ramki, jej powierzchni S oraz wartości indukcji pola magnetycznego B.

W ramce obracającej się w polu magnetycznym przepływa zatem prąd o napięciu sinusoidalnie zmiennym. Jest on zwany prądem przemiennym.

Maksymalna wartość SEM indukcji (którą od tej chwili nazywać będziemy napięciem prądu przemiennego U), powstającej, kiedy ramka ustawiona jest prostopadle do linii siło pola, wynosi:

Tę maksymalną wartość nazywamy amplitudą napięcia prądu przemiennego.

Natężenie wzbudzanego w ramce prądu indukcyjnego również zmienia się sinusoidalnie według wzoru:

gdzie I₀ oznacza amplitudę natężenia prądu przemiennego.

Napięcie i natężenie prądu przemiennego w obwodzie są zgodne w fazie, a wiążą się ze sobą zależnością:

gdzie R jest oporem obwodu.

PRACA I MOC PRĄDU PRZEMIENNEGO

Jak wiemy, moc prądu P wydzielana na oporze R w postaci ciepła dana jest wzorem:

lub

Moc prądu przemiennego, w którym napięcie i natężenie są zmienne, również zmienia się sinusoidalnie w czasie:

a jej wartość maksymalna wynosi:

.

Zależność mocy prądu przemiennego od czasu przedstawia się następująco:

Moc określana powyższym wzorem nazywana jest mocą chwilową prądu przemiennego. Jeżeli uśrednimy ją w czasie, otrzymamy inny wzór:

Wielkość P_sk nazywamy mocą skuteczną lub czynną. Widzimy, że jest ona wprost proporcjonalna do kwadratu amplitudy natężenia prądu i nie zależy od jego częstotliwości.

Praca W, którą prąd przemienny wykonuje w czasie jednego okresu T, równa się mocy skutecznej prądu pomnożonej przez długość tego okresu, i dana jest wzorem:

Praca ta jest równa polu pod wykresem zależności mocy prądu przemiennego od czasu.

NATĘŻENIE I NAPIĘCIE SKUTECZNE

Pojęcia natężenia i napięcia skutecznego wiążą się z pracą prądu przemiennego i mocą wydzielaną na włączonych w obwód oporach omowych.

Natężenie skuteczne I_sk prądu przemiennego jest równe natężeniu prądu stałego, który w określanym czasie t wykonuje taką samą pracę, jak prąd przemienny (czyli taki, którego moc jest taka sama, jak prądu przemiennego).

Porównując wartości mocy prądu przemiennego i stałego (o natężeniu równym I_sk) w jednym równaniu, otrzymujemy:

Z równania tego możemy obliczyć wartość I_sk:

Analogiczny związek zachodzi między U_sk i amplitudą napięcia U₀:

Moc skuteczną prądu przemiennego możemy zatem zapisać wzorem:

Amperomierze, woltomierze i watomierze włączone do obwodów prądu przemiennego mierzą wartości skuteczne I_sk, U_sk i P_sk, a wartości maksymalne wyznaczamy, mnożąc otrzymane wyniki przez
.

TRANSFORMATOR

Transformatorem nazywamy urządzenie służące do przekształcania (zwiększania lub zmniejszania) napięcia prądów przemiennych. Wykorzystujemy w tym celu zjawisko indukcji elektromagnetycznej. Transformator składa się z dwóch połączonych uzwojeń o liczbach zwojów n₁ i n₂, nazywanych uzwojeniem pierwotnym i wtórnym. Uzwojenie pierwotne (n₁) jest podłączane do napięcia U₁, które chcemy przełączyć na napięcie U₂, i łączone z uzwojeniem wtórnym (n₂). W zależności od stosunku liczby zwojów w obu uzwojeniach napięcie U₂ będzie większe lub mniejsze od napięcia U₁:

Stosunek napięcia U₂ do napięcia U₁, równy stosunkowi liczby zwojów w uzwojeniu wtórnym do liczby zwojów w uzwojeniu pierwotnym, nazywamy przekładnią transformatora k:

Gdy k < 1 (n₂ < n₁), transformator obniża napięcie, a gdy k > 1 (n₂ > n₁), podwyższa je.

Odbiornik o oporze R, podłączony do obwodu wtórnego, potrzebną mu moc P₂ pobiera z elektrowni za pośrednictwem obwodu pierwotnego. Ponieważ jednak przepływ prądu przez transformator powoduje straty energii, wydzielanej w postaci ciepła na obu uzwojeniach, moc P₁ pobierana przez obwód pierwotny musi być odpowiednio większa od mocy P₂.

Stosunek mocy potrzebnej odbiorcy w obwodzie wtórnym P₂ do mocy pobieranej P₁ jest nazywany sprawnością transformatora η:

Dla większości transformatorów wartość sprawności mieści się między 0,9 a 1.

Wartość η = 1 posiadałby nie istniejący w rzeczywistości transformator idealny. Dla takiego transformatora możemy zapisać zależność:

a zatem

Wynika stąd, że:

Natężenie skuteczne prądu w obwodzie wtórnym jest zatem odwrotnie proporcjonalne do przekładni transformatora.

Wynikają z tego następujące wnioski:

1. transformator o przekładni k > 1 napięcie zwiększa k razy, a natężenie prądu zmniejsza k razy;

2. transformator o przekładni k < 1 napięcie zmniejsza k razy, a natężenie prądu zwiększa k razy.

OPÓR R W OBWODZIE PRĄDU PRZEMIENNEGO

Dla oporu omowego R umieszczonego w obwodzie prądu przemiennego (
,
):

1. Napięcie chwilowe na oporze R jest zgodne w fazie z natężeniem chwilowym prądu I:

2. Moc skuteczna wydzielana na oporze omowym R w postaci ciepła wynosi:

POJEMNOŚĆ C W OBWODZIE PRĄDU PRZEMIENNEGO

Kondensator o pojemności C podłączony do źródła prądu stałego o napięciu U ładuje się, gromadząc na okładkach ładunek Q = CU. Gdy napięcie na kondensatorze zrówna się wartością z napięciem źródła, prąd ładowania zanika. Na okładki kondensatora przestaje wchodzić ładunek. Kondensatory nie przewodzą zatem stałych prądów.

Rozważmy w takim razie kondensator o pojemności C podłączony do źródła prądu przemiennego:

Sytuacja jest tutaj nieco inna — ponieważ napięcie prądu jest sinusoidalnie zmienne, ładunek Q gromadzony na okładkach kondensatora również zmienia się sinusoidalnie w czasie. Oznacza to, że kondensator ładuje się do wartości maksymalnej
, następnie rozładowuje się całkowicie (Q = 0), po czym ponownie ładuje maksymalnie, z tym że w przeciwną stronę (znaki ładunków na okładkach zmieniają się na przeciwne) i znowu rozładowuje do zera.

Natężenie chwilowe prądu płynącego przez kondensator jest związane ze zmianą ładunku na okładkach kondensatora w następujący sposób:

Widzimy zatem, że:

1. napięcie chwilowe na kondensatorze U_c jest opóźnione w fazie względem natężenia chwilowego prądu o kąt
   ;

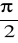
2. amplituda natężenia prądu I₀ ma wartość:

3. stosunek:

pełni w rozważanym obwodzie funkcję efektywnego oporu elektrycznego i nosi nazwę oporu pojemnościowego R_C; jest on odwrotnie proporcjonalny do częstotliwości υ prądu przemiennego;

4. natężenie skuteczne prądu przemiennego płynącego przez kondensator, wyznaczane z zależności:

jest wprost proporcjonalne do częstotliwości υ prądu przemiennego — kondensator dławi zatem prądy o niskiej częstotliwości, a prądom o wysokiej częstotliwości stawia niewielki opór;

5. moc skuteczna wydzielana na kondensatorze w czasie jednego okresu T jest równa zeru.

INDUKCYJNOŚĆ L W OBWODZIE PRĄDU PRZEMIENNEGO

Rozważmy zwojnicę o indukcyjności L, umieszczoną w obwodzie prądu przemiennego:

Indukcyjność L zwojnicy zależy od jej wymiarów i kształtu w następujący sposób:

gdzie l jest długością zwojnicy,

n — liczbą zwojów,

S — polem przekroju poprzecznego zwojnicy,

μ₀ — przenikalnością magnetyczną próżni,

μ — przenikalnością magnetyczną ośrodka wypełniającego zwojnicę.

Prąd przemienny o natężeniu
indukuje w zwojnicy SEM samoindukcji ξ_L równą:

W obwodzie są zatem dwa źródła prądu: podłączone z zewnątrz sinusoidalnie zmienne napięcie
i indukująca się w zwojnicy SEM samoindukcji.

Ponieważ zakładamy, że w naszym obwodzie nie znajduje się opór omowy R, możemy opisać ten obwód następującymi zależnościami:

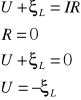
Stąd napięcie chwilowe na zwojnicy U_L jest równe:

Widzimy zatem, że:

1. napięcie chwilowe na zwojnicy wyprzedza w fazie natężenie chwilowe prądu o kąt
   ;

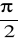
2. amplituda natężenia prądu I₀, wyznaczona z zależności:

ma wartość:

3. stosunek:

pełni w rozważanym obwodzie funkcję efektywnego oporu elektrycznego i nosi nazwę oporu indukcyjnego R_L lub reaktancji:

i jest wprost proporcjonalny do częstotliwości υ prądu przemiennego;

4. natężenie skuteczne prądu przemiennego, wyliczane z zależności:

jest odwrotnie proporcjonalne do częstotliwości υ prądu przemiennego — zwojnica tłumi zatem prądy o wysokiej częstotliwości, a prądom o niskiej częstotliwości stawia niewielki opór;

5. moc skuteczna wydzielana na indukcyjności L w czasie jednego okresu T jest równa zeru.

---