BUDOWA ATOMU — CZĄSTKI ELEMENTARNE

Atom każdego pierwiastka składa się z dodatnio naładowanego jądra, znajdującego się w jego geometrycznym środku, i z pozajądrowego układu ujemnie naładowanych elektronów. Łączny ładunek elektronów jest równy co do wartości ładunkowi jądra, dlatego też atom jako całość jest elektrycznie obojętny.

Masa elektronu jest niewielka w porównaniu z masą jądra i stanowi ok. 0,0005434 u, czyli 1/1840 u. Wartość zgromadzonego na elektronie ładunku wynosi 1,6 ·10^-19 C i zwana jest ładunkiem elementarnym. Ładunek ten ma symbol e, w odróżnieniu od symbolu e^-, stosowanego dla elektronu. Przyłączenie lub odłączenie od atomu jednego elektronu czyni z niego jon ujemny lub dodatni.

W skład jądra wchodzą dwa rodzaje cząstek: protony i neutrony. Mają one zbliżone masy, ok. 1 u, różnią się natomiast ładunkiem elektrycznym. Neutron jest elektrycznie obojętny, a na protonie skupiony jest elementarny ładunek dodatni. Obecność neutronów w jądrze atomowym zapobiega jego rozpadowi w wyniku wzajemnego elektrostatycznego odpychania protonów. Rozmiary jądra są 10⁴ - 10⁵ razy mniejsze od rozmiarów atomu jako całości, ale jest w nim skupiona niemal cała jego masa.

Liczba protonów w jądrze atomu, równa łącznej liczbie elektronów krążących po orbitach, nazywana jest liczbą atomową (Z), natomiast łączna liczba protonów i neutronów budujących jądro nazywa się liczbą masową (A).

TEORIE NAUKOWE DOTYCZĄCE BUDOWY ATOMU:

TEORIA RUTHEFORDA:

Jako pierwszy, na początku XX wieku, Ernest Rutheford opracował planetarny model budowy atomu. Zgodnie z tym modelem elektrony miały krążyć wokół jądra z olbrzymią szybkością po kołowych albo eliptycznych orbitach, a rolę siły dośrodkowej miała spełniać siła elektrostatycznego przyciągania elektronów przez jądro.

Teoria Rutheforda stała jednak w sprzeczności z prawami elektrodynamiki Maxwella, zgodnie z którymi krążący wokół jądra elektron musiałby bez przerwy emitować promieniowanie elektromagnetyczne o systematycznie rosnącej długości fali, tracąc przy okazji zarówno energię, jak i prędkość. W konsekwencji poruszałby się on ruchem spiralnym, aby w końcu spaść na jądro. Tymczasem nie obserwuje się ani spadania elektronu na jądro, ani emisji promieniowania w zwykłych warunkach. Emisja taka, w postaci fal świetlnych o ściśle określonej długości (charakterystycznej dla każdego pierwiastka) możliwa jest tylko po uprzednim doprowadzeniu energii — np. po ogrzaniu do wysokiej temperatury.

TEORIA BOHRA:

W roku 1913 duński fizyk Niels Bohr zaproponował inną teorię, opierającą się na trzech podstawowych postulatach:

1. elektrony krążą wokół jądra po tzw. orbitach stacjonarnych, czyli po ściśle określonych torach w kształcie okręgów, i poruszając się po tych orbitach nie tracą energii;

2. energia elektronu jest skwantowana, tzw. orbity stacjonarne znajdują się się w różnej odległości od jądra, a każdej z nich odpowiadała określona wartość energii elektronu;

3. przeskok elektronu z jednej orbity na drugą dawałby zysk lub stratę określonej porcji energii — tzw. kwantu, którego wartość określa równanie Plancka:

E = h · υ

gdzie E oznacza wartość energii,

h — tzw. stałą Plancka, czyli 6,625 ·10^-34 J ·s

υ — częstotliwość absorbowanego lub emitowanego promieniowania.

Oznacza to, że „przeskokowi” elektronu na niższą orbitę towarzyszy wyemitowanie kwantu energii hυ w postaci fali świetlnej o częstotliwości υ, i analogicznie — dostarczenie mu kwantu energii za pośrednictwem fali świetlnej o odpowiedniej częstotliwości spowoduje przejście elektronu z orbity niższej na wyższą.

Klasyczna teoria atomu Bohra opisuje najprostszy z atomów — atom wodoru, w którym w polu jądra porusza się tylko jeden elektron.

Rozkład sił działających na elektron przedstawia się równaniem:

gdzie e oznacza ładunek elementarny,

m — masę elektronu,

r_n — promień n-tej orbity,

ε_o — bezwzględną przenikalność dielektryczną próżni.

Całkowita energia elektronu jest z kolei sumą jego energii potencjalnej i kinetycznej:

lub, w uproszczeniu i po podstawieniu wartości r_n:

Zależność ta podaje wartość energii elektronu na n-tej orbicie.

Liczba n, określająca wartość całkowitej energii E na orbicie o promieniu r_n nosi nazwę głównej liczby kwantowej.

MECHANIKA KWANTOWA

Najnowszą, do dziś aktualną teorią budowy atomu jest mechanika kwantowa, której początki sięgają lat 20-tych naszego stulecia. Narodziła się dzięki pracom de Broglie'a, Heisenberga, Schrödingera, Diraca i wielu innych naukowców, a jej głównym założeniem jest dualizm korpuskularno-falowy materii. Okazuje się, że nie tylko promieniowanie, ale również elektrony, atomy i cząsteczki mogą w pewnych warunkach zachowywać się tak, jakby były falą (na ogół o bardzo małej długości). Zajmując się zagadnieniem dualizmu materii, mechanika i elektrodynamika kwantowa nie posługują się poglądowymi obrazami i modelami, lecz wprowadzają abstrakcyjne pojęcia i matematyczne opisy, niezbędne do ujęcia i opisania rzeczywistości mikroświata.

• Zasada nieoznaczoności Heisenberga. Zasada ta głosi, że nie można jednocześnie wyznaczyć z dowolnym stopniem dokładności położenia i pędu (prędkości) cząstki. Można jedynie mówić o określonym prawdopodobieństwie znalezienia się jej w pewnym elemencie przestrzeni z pewnym, niezupełnie ściśle określonym pędem.

Zasadę nieoznaczoności w odniesieniu do położenia i pędu można określić mniej więcej tak: iloczyn niepewności położenia i niepewności pędu jest nie mniejszy niż h/2π:

Widać zatem, że im dokładniej będzie wyznaczona jedna z tych wielkości, tym większą niepewnością będzie obarczona druga. Nie wynika to z błędów wynikających z niedokładności pomiarów, ale ze swoistego, nie znanego fizyce klasycznej, zachowania się mikroobiektów.

Zasada nieoznaczoności dotyczy także innych par wielkości, np. energia - czas:

Mówimy o niej np. w następującym przypadku: jeżeli atom przebywa na wyższym poziomie energetycznym przez czas bardzo krótki, a potem przechodzi do stanu niższego, w którym może przebywać nieograniczenie długo, to energia emitowanego przy tym fotonu nie będzie wielkością dokładnie określoną. Niepewność energii ΔE jest bardzo duża, bo niepewność czasu Δt jest bardzo mała.

Nie znamy żadnego zjawiska, które byłoby sprzeczne z zasadą nieoznaczoności. Zasada nieokreśloności dotyczy wszystkich obiektów mikro- i makroskopowych

Jednak w ujęciu praktycznym niepewność pomiaru położenia dla obiektów makroskopowych jest zaniedbywalnie mała, natomiast w odniesieniu do elektronu ma ogromne znaczenie. Innymi słowy, trudno mówić o pojęciu jego „toru”; zastępujemy je innym — prawdopodobieństwem znalezienia się elektronu w określonej przestrzeni wokółjądrowej. Elektron w ujęciu mechaniki kwantowej oznacza zatem „chmurę” ładunku ujemnego, w której różnych rejonach pojawia się z różnym prawdopodobieństwem. Chmura taka w atomie wodoru, w stanie o najniższej energii (tzw. stan podstawowy), ma symetrię kulistą, a jej gęstość (gęstość elektronowa, objętościowa gęstość ładunku) maleje asymptotycznie w miarę wzrostu odległości od jądra i największa jest w rejonie przyjądrowym. Choć granice chmury teoretycznie rozciągają się do nieskończoności, w praktyce w odległości kilkuset pikometrów od jądra jej gęstość jest praktycznie równa zero.

• Właściwości falowe materii. Dowiedziono, że każdemu posiadającemu masę ciału poruszającemu się z pewną prędkością odpowiada fala o oznaczonej długości. Długość takiej fali, zwanej falą de Broglie'a, wiąże się z pędem ciała (cząstki) zależnością:

gdzie λ oznacza długość fali

h — stałą Plancka

m — masę ciała lub cząstki

a v — jego prędkość.

Jak widać, w przypadku ciał makroskopowych długość fali jest wielkością niewyobrażalnie małą. W przypadku mikrocząstek nabiera ona jednak znaczących rozmiarów — np. elektronowi o prędkości 5,84 ·10⁷ m/s odpowiada fala o długości 0,0123 nm, a więc porównywalnej z długościami fali promieniowania rentgenowskiego.

• Równanie Schrödingera. Występowanie falowych cech cząstek prowadzi do wniosku, że ich stan powinna opisywać jakaś funkcja reprezentująca proces falowy. Oznaczamy ją przez Ψ i nazywamy krótko funkcją falową. Niekiedy jest ona nazywana falami prawdopodobieństwa i jest zawsze funkcją zespoloną, to jest sumą funkcji rzeczywistej i urojonej. Wielkością stosowaną w praktyce jest kwadrat modułu tej funkcji — jest on miarą prawdopodobieństwa, że cząstka znajdzie się w określonym elemencie objętości przestrzeni.

Kwadrat modułu funkcji Ψ nazywamy zatem niekiedy gęstością prawdopodobieństwa znalezienia cząstki w danym fragmencie przestrzeni.

Funkcję Ψ otrzymujemy, rozwiązując tzw. amplitudowe równanie Schrödingera, podstawowe w mechanice kwantowej nierelatywistycznej. Równanie to ma bardzo złożoną postać matematyczną, dość jednak powiedzieć, że jedną z występujących w nim wielkości jest energia (E). Otóż w teorii kwantowej różniczkowej dowodzi się, że równanie tego typu ma rozwiązania nie dla dowolnych, lecz wyłącznie dla ściśle określonych wartości E. W ten sposób równanie falowe Schrödingera udowadnia, że energia elektronu związanego w atomie jest wielkością skwantowaną.

BUDOWA ATOMU — REGUŁY I PRAWA

LICZBY KWANTOWE

Wyróżniamy pięć parametrów ruchu elektronu, które podlegają kwantowaniu. Opisuje je odpowiednio pięć liczb kwantowych.

1. Główna liczba kwantowa n.

Liczba ta kwantuje energię elektronu w atomie wodoru, co w uproszczeniu przedstawia się równaniem:

gdzie E₁ — bezwzględna wartość energii elektronu w stanie podstawowym, równa 13,6 eV

(rzeczywista wartość energii jest bowiem liczbą ujemną)

n — główna liczba kwantowa.

Liczba n może przyjmować wartości kolejnych liczb naturalnych:

n = 1, 2, 3, … , ∞

Zbiór stanów kwantowych o tej samej wartości głównej liczby kwantowej nazywamy poziomem energetycznym (lub powłoką elektronową). Liczba stanów kwantowych o tej samej wartości głównej liczby kwantowej wynosi 2n², liczba poziomów orbitalnych — n².

Liczbę kwantową główną oznaczamy dużymi literami, poczynając od K dla n = 1, a następnie L, M, N, O, P… Tymi samymi symbolami literowymi oznaczamy kolejne poziomy energetyczne (powłoki elektronowe).

Jak zaznaczono na wstępie, liczba n kwantuje energię elektronu w atomie wodoru. W atomach innych pierwiastków na wartość energii elektronu mają wpływ dwie liczby kwantowe: główna i poboczna (l). Różnica wynika stąd, że w atomie wodoru na elektron działa jedynie elektrostatyczne przyciąganie jądra atomowego (protonu), a w atomach wieloelektronowych — również elektrostatyczne odpychanie wszystkich pozostałych elektronów układu.

2. Poboczna (orbitalna) liczba kwantowa l.

Liczba ta kwantuje orbitalny moment pędu elektronu (L), a w atomach wieloelektronowych wraz z główną liczbą kwantową opisuje stan energetyczny elektronu.

gdzie L — orbitalny moment pędu elektronu; wielkość wektorowa

Liczba l przyjmuje następujące wartości (w łącznej liczbie n):

l = 0, 1, 2, … , (n - 1)

Zbiór stanów kwantowych o tej samej wartości pobocznej i głównej liczby kwantowej nazywamy podpoziomem energetycznym (podpowłoką elektronową). Każdej podpowłoce przyporządkowany jest odpowiedni symbol literowy, w zależności od pobocznej liczby kwantowej. Liczba podpowłok elektronowych w danej powłoce wynosi n. W powłoce K (n = 1) jest jedna podpowłoka s, w powłoce L (n = 2) — podpowłoki s i p, w powłoce M (n = 3) podpowłoki s, p, d, w powłoce N (n = 4) — podpowłoki s, p, d, f itd. już w kolejności alfabetycznej.

Przy pomocy liczby l możemy określić również liczbę stanów kwantowych w podpowłoce (jako równą 4l + 2) i liczbę poziomów orbitalnych w podpowłoce (2l + 1).

3. Magnetyczna liczba kwantowa m.

Liczba ta kwantuje orientację przestrzenną orbitalnego momentu pędu elektronu (M). Jej kolejne wartości to wartości rzutu wektora orbitalnego momentu pędu elektronu na określony kierunek w przestrzeni (np. linie zewnętrznego pola magnetycznego), innymi słowy wektor L może ustawiać się tylko w taki sposób, aby jego rzut w wyróżnionym kierunku przyjmował wartości określone liczbą m:

gdzie m jest wartością magnetycznej liczby kwantowej.

Liczba m przyjmuje następujące wartości (w łącznej liczbie 2l+1):

m = -l, -(l - 1), … , -1, 0, 1, … , (l - 1), l

gdzie l oznacza poboczną liczbę kwantową.

Magnetyczna liczba kwantowa określa liczbę poziomów orbitalnych w danej podpowłoce (jako równą 2l+1).

Zbiór stanów kwantowych opisanych tym samym zespołem liczb kwantowych n, l, m jest nazwany obszarem orbitalnym.

4. Spinowa liczba kwantowa s.

Liczba ta kwantuje wewnętrzny moment pędu elektronu.

Elektron charakteryzuje się pewnym rodzajem ruchu wewnętrznego, nieprzekładalnym na zjawiska makroskopowe, ale dającym efekty w przybliżeniu przypominające efekty obrotu wokół własnej osi. Wewnętrzny moment pędu został nazwany spinem; obok masy i ładunku jest to podstawowa właściwość charakteryzująca elektron jako cząstkę. Spin elektronu jest wielkością wektorową odpowiada za magnetyczne właściwości elektronu (dipola magnetycznego).

Spinowa liczba kwantowa przyjmuje tylko jedną wartość:

przy opisie stanu kwantowego elektronu można ją zatem pominąć.

5. Magnetyczna spinowa liczba kwantowa m_s.

Liczba ta opisuje orientację przestrzenną wektora spinu. Wektor ten może ustawić się w zewnętrznym polu magnetycznym tylko tak, aby jego rzut na kierunek tego pola przyjmował jedną z dwóch możliwych wartości — są to dwie dopuszczalne wartości magnetycznej spinowej liczby kwantowej.

Każdy obszar orbitalny (opisany liczbami n, l, m) stanowią dwa STANY KWANTOWE, różniące się między sobą jedynie magnetyczną spinową liczbą kwantową.

OBSZAR ORBITALNY

Jak już wspomniano, obszarem orbitalnym nazywamy zbiór stanów kwantowych opisanych tym samym zespołem liczb kwantowych n, l, m. Jest to pewien wyznaczony obszar przestrzeni wokółjądrowej, na zewnątrz którego gęstość ładunku jest zaniedbywalnie mała — mniejsza od założonej wartości granicznej — a jednocześnie wewnątrz niego jest od tej wartości większa.

Wewnątrz obszaru orbitalnego mieści się niemal cały ładunek elektronu, a prawdopodobieństwo jego znalezienia w tym obszarze ma znaczną, założoną wartość rzędu 90-95%.

Na parametry obszaru orbitalnego mają wpływ trzy liczby kwantowe:

• główna liczba kwantowa n decyduje o jego rozmiarach;

• poboczna liczba kwantowa l — o jego kształcie;

• magnetyczna liczba kwantowa m — o jego orientacji przestrzennej.

REGUŁY DOTYCZĄCE OBSADZANIA STANÓW KWANTOWYCH

Zajmowaniem stanów kwantowych w atomach wieloelektronowych rządzą dwie główne reguły:

1. Reguła Hunda mówiąca, że:

• w danej podpowłoce powinna znajdować się możliwie największa liczba niesparowanych elektronów;

• pary elektronowe (↑↓) tworzą się dopiero po zajęciu wszystkich poziomów orbitalnych danej podpowłoki przez niesparowane elektrony;

• niesparowane elektrony zajmujące poziomy orbitalne danej podpowłoki mają identyczną orientację spinu.

2. Zasada Pauliego (zakaz Pauliego), mówiący, że:

w danym układzie atomowym nie mogą istnieć dwa lub więcej elektronów, których stan określałyby takie same dla obu liczby kwantowe.

Innymi słowy, każdy elektron w atomie musi się różnić od pozostałych wartością przynajmniej jednej liczby kwantowej.

WIDMO ABSORPCYJNE I EMISYJNE ATOMU WODORU

Korzystając z trzeciego postulatu Bohra można znaleźć energię fotonów, a więc i częstości drgań promieniowania emitowanego (lub absorbowanego) podczas różnych przejść elektronu z jednego poziomu energetycznego na inny.

E = h · υ

hυ = E_m - E_n

gdzie m oznacza główną liczbę kwantową poziomu o wyższej energii, a n — poziomu o energii niższej.

Stąd wyliczyć można, że:

gdzie n i m są wartościami liczb kwantowych rozważanych powłok

W spektroskopii praktycznej korzysta się często z pojęcia tzw. liczby falowej υ, równej liczbowo odwrotności długości fali λ. (Liczba falowa jest to po prostu liczba długości fal mieszcząca się na odcinku 1 m).

Posługując się liczbą falową powyższe równanie możemy zapisać:

Czynnik przed nawiasem jest wielkością stałą. Oznaczamy ją literą R i nazywamy stałą Rydberga.

R =
= 1,0974 · 10⁷ · m^-1

Po jej podstawieniu wzór przybiera prostszą postać:

Wzór powyższy zaliczamy do tzw. wzorów seryjnych, czyli takich, do których możemy podstawiać liczne serie wartości. W każdej serii n ma wartość stałą (np. 1, 2, 3, 4…), zaś m przybiera wartości od n + 1 do nieskończoności.

Każdej serii odpowiada zbiór linii widmowych, ułożonych w widmie w ten sposób, że seria zaczyna się zawsze od strony fal dłuższych i o mniejszej częstości i biegnie w stronę fal krótszych. Jednocześnie odstępy między sąsiednimi liniami widmowymi maleją regularnie, a natężenie linii staje się coraz mniejsze; w końcu linie zagęszczają się tak, że nie jesteśmy już w stanie obserwować ich oddzielnie — mówimy, że seria linii dąży do granicy odpowiadającej teoretycznie m → ∞.

Seria widmowa powstająca przy przejściach emisyjnych w atomie wodoru na poziom n = 2 z poziomów wyższych, leżąca w dużej części w widzialnym obszarze widma, nosi nazwę serii Balmera.

Znane są też inne serie widma wodoru, nazywane od nazwisk ich odkrywców. Są nimi: seria Lymana (powstaje przy przejściu elektronów z poziomu m = 2, 3, 4… na poziom n = 1) leżąca w dalekim nadfiolecie) oraz serie: Paschena (n = 3), Bracketta (n = 4), Pfunda (n = 5) i Humpreyhsa (n = 6), leżące w podczerwieni.

Powyższe rozważania dotyczą widma emisyjnego atomu wodoru. Rozpatrując absorpcję, czyli zjawisko pochłaniania fotonu o częstości υ, należałoby w dwóch pierwszych wzorach zamienić miejscami m i n.

PROMIENIOWANIE TERMICZNE

DEFINICJA PROMIENIOWANIA TERMICZNEGO

Wszystkie ciała, których temperatura jest wyższa od zera bezwzględnego (0˚K, ok. -273˚C) są źródłami promieniowania. Promieniowanie widzialne emitują ciała ogrzane do temperatury ok. 773˚K (ok. 500˚C), tzn. temperatury „czerwonego żaru”. Promieniowanie tego typu nosi nazwę promieniowania termicznego albo temperaturowego. Czerpie ono swoją energię z ruchów termicznych atomów i cząsteczek.

Rzecz jasna, ciało promieniujące stopniowo traci energię i oziębia się, jeżeli nie są w nim czynne jakieś dodatkowe źródła energii. Stan równowagi ustala się, gdy ilość energii wypromieniowanej w jednostce czasu równa się ilości energii promieniowania pochłoniętego przez ciało. Wówczas temperatura ciała pozostaje stała, a jego promieniowanie nazywamy zrównoważonym.

CIAŁO DOSKONALE CZARNE

Prawa promieniowania termicznego dotyczą w większości przypadków emisji i absorpcji promieniowania ciała doskonale czarnego. Samo ciało doskonale czarne nie istnieje jednak w przyrodzie. Jego modelem może być komora o nieprzenikliwych dla energii ściankach, z niewielkim otworkiem w jednej z nich. Promieniowanie wpadające przez otwór do wnętrz komory ma znikomą szansę wyjścia na zewnątrz, ponieważ przy każdym odbiciu od wewnętrznej ścianki część energii zostaje pochłonięta.

model ciała

doskonale

czarnego:

Zdolność emisyjna ciała doskonale czarnego E_λ,T, zwana też gęstością mocy promieniowania, jest wielkością umożliwiającą scharakteryzowanie natężenia promieniowania emitowanego w danej temperaturze T i w pewnym przedziale długości fal λ, λ + ∆λ widma tego ciała.

E_λ,T jest to ilość energii emitowana w jednostce czasu w kącie bryłowym 2π z jednostki powierzchni o temperaturze T w pewnym przedziale długości fal ∆λ.

gdzie R_T jest strumieniem energii emitowanej w danej temperaturze z 1 m² powierzchni w czasie 1 s we wszystkich długościach fali, w kącie bryłowym 2π.

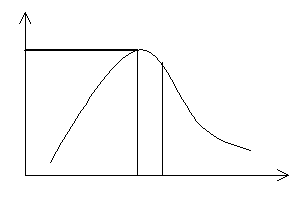
Zależność E_λ,T od λ przedstawia rysunek:

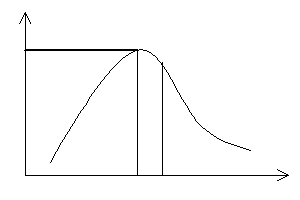
Powierzchnia zacienionego prostokąta daje energię promieniowania emitowanego we wszystkich kierunkach w kącie bryłowym półpełnym w ciągu 1 s z powierzchni 1 m² dla fal o długości zawartej w granicach λ; λ + ∆λ. Całe pole pod krzywą reprezentuje całkowitą moc emitowaną przez ciało z jednostki powierzchni.

Z wartością E_λ,T ciała doskonale czarnego wiąże się pojęcie gęstości energii u_λ,T promieniowania zrównoważonego w komorze, wyrażane bardzo prostym wzorem:

Zdolnością absorpcyjną A_λ,T ciała nazywamy stosunek energii pochłoniętej przez ciało do padającej na nie; jest ona funkcją temperatury T i długości fali λ. Dla ciała doskonale czarnego zdolność absorpcyjna A_λ,T jest równa 1. Dla ciał rzeczywistych zdolność ta jest zawsze mniejsza od jedności.

PRAWA DOTYCZĄCE PROMIENIOWANIA TERMICZNEGO

1. Prawo Kirchhoffa. Kirchhoff udowodnił na podstawie praw termodynamiki, że dla wszystkich substancji rzeczywistych zdolność emisyjna E_λ,T jest proporcjonalna do ich zdolności absorpcyjnej A_λ,T.

Prawo Kirchhoffa jest słuszne nie tylko dla globalnej emisji i absorpcji, ale i dla każdej długości fali rozpatrywanej oddzielnie. Jeżeli ujmiemy je bardziej ogólnie, zauważymy jego związek z prawem termometrii o wyrównywaniu się temperatur — sens tego prawa został dodatkowo rozciągnięty na promieniowanie. Innymi słowy, gdyby zdolności emisyjna i absorpcyjna nie były do siebie proporcjonalne, niemożliwa byłaby równowaga między promieniowaniem a materią, doświadczenie zaś dowodzi, że taka równowaga istnieje, ustala się szybko i jest wyjątkowo trwała.

Często prawo Kirchhoffa formułuje się jeszcze inaczej: dla wszystkich ciał stosunek zdolności emisyjnej E_λ,T do ich zdolności absorpcyjnej A_λ,T jest tą samą funkcją (λ;T).

stąd wniosek, że w danej temperaturze ciało pochłania najsilniej te długości fal, które samo emituje.

Ponieważ dla ciała doskonale czarnego A_λ,T = 1, więc:

f(λ;T) = E_λ,T

Prawo Kirchhoffa można zatem ująć w jeszcze innej, bardziej precyzyjnej formie: stosunek zdolności emisyjnej ciała do jego zdolności absorpcyjnej jest równy zdolności emisyjnej ciała doskonale czarnego.

2. Prawo Stefana-Boltzmanna. Prawo to głosi, że całkowita energia R_T emitowana przez 1 m² powierzchni ciała doskonale czarnego w ciągu 1 s dla wszystkich długości fal widma jest proporcjonalna do czwartej potęgi temperatury bezwzględnej.

gdzie

Dla ciał rzeczywistych prawo Stefana-Boltzmanna wymaga zazwyczaj zastosowania innej wartości współczynnika σ oraz innego wykładnika potęgi przy T niż dla ciała czarnego. Wykładnik ten jest z reguły liczbą niecałkowitą i zmienia się wraz z temperaturą.

3. Prawo Wiena. Prawo to dotyczy rozkładu energii w widmie ciała doskonale czarnego. Mówi ono, że długość fali λ_max, na którą przypada maksimum energii promieniowania ciała doskonale czarnego, zależy od temperatury ciała T. Im wyższa temperatura, tym mniejsza jest λ_max. Związek między tymi dwiema wielkościami ma postać:

λ_max · T = const = 2898 μm · K

Ilustracją prawa Wiena może być następujący rysunek:

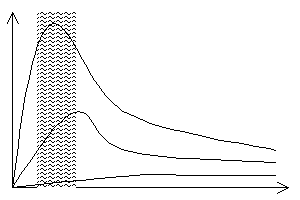
(prostokąt zacieniowany oznacza widzialną część promieniowania świetlnego)

Im niższa temperatura, tym większa część energii widma przypada na fale dłuższe, np. na czerwień lub podczerwień. (Dlatego np. tak nieekonomiczne jest oświetlenie za pomocą tradycyjnych żarówek: zauważmy, że w temperaturze drucika żarówki, wynoszącej około 2800˚K, maksimum energii promieniowania przypada na niewidzialną — a zatem nieprzydatną — długość fali znajdującą się w podczerwieni). Gdy temperatura ciała wzrasta, λ_max maleje, przesuwając się od barwy czerwonego żaru przez pomarańczową i żółtą aż do tzw. „białego żaru”, a w temperaturze gwiazd — do barwy niebieskawej.

Praktyczne wykorzystanie prawa Wiena polega np. na wyznaczaniu temperatury ciał na podstawie długości λ_max. Zakłada się przy tym, że badane obiekty zachowują się jak ciała doskonale czarne.

4. Prawo Plancka.

Otrzymane na drodze doświadczalnej wyniki rozkładu energii w widmie ciała doskonale czarnego nie zgadzały się z wynikami rozważań teoretycznych, zakładających emisję promieniowania w sposób ciągły. Niezgodność krzywych doświadczalnych i teoretycznych występowała w środkowej części widm, tj. w okolicy maksimum krzywej. Niezgodność tę wyjaśnił Planck. Jego hipoteza (ok. 1900 r.) o nieciągłym charakterze emisji fali świetlnej pozwoliła w wyniku rozważań teoretycznych uzyskać zależność doskonale zgodną z wynikami doświadczalnymi.

Jak wiemy, hipoteza Plancka zakłada, że promieniowanie jest emitowane w postaci kwantów energii (fotonów) o energii:

Z teorii Plancka wynika, że zależność między energią E_λ,T, przypadającą na długość fali λ w temperaturze T, a daną długością fali λ ma znacznie bardziej skomplikowaną postać:

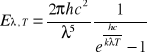
gdzie h jest stałą Plancka

a k = 1,38 · 10^-23 J/K — stałą uniwersalną (stałą Boltzmanna).

ZJAWISKA TERMOELEKTRYCZNE

MOLEKULARNA BUDOWA KRYSZTAŁÓW METALI

Kryształ metalu zbudowany jest z dodatnich jonów (utworzonych przez jądra atomowe i elektrony zrębu atomowego) oraz tzw. gazu elektronowego — swobodnie poruszających się między tymi jonami elektronów walencyjnych (stwierdzono jednak, że nie wszystkie elektrony walencyjne muszą przechodzić do gazu elektronowego). Gaz elektronowy jest przyciągany przez kationy metalu siłami elektrostatycznymi.

Kryształy takie tworzą zarówno czyste metale, jak i ich stopy. Z obecnością wolnych elektronów wiążą się typowe właściwości metali, m. in. doskonałe przewodnictwo cieplne i elektryczne.

Gdy przewodnik nie znajduje się pod działaniem zewnętrznego pola elektrycznego, elektrony swobodne poruszają się nieuporządkowanym ruchem w wielu kierunkach. Kiedy jednak przyłożymy zewnętrzne pole elektryczne o stałym kierunku natężenia, wówczas elektrony uzyskują składową prędkości w kierunku od potencjału niższego do wyższego (mówimy wówczas o przepływie prądu przez przewodnik, oczywiście w kierunku odwrotnym).

Aby elektron mógł wyjść poza obręb metalu, musi mieć dostatecznie dużą energię umożliwiającą mu pokonanie siły oddziaływania z dodatnimi jonami sieci. Najmniejszą wartość tej energii nazywamy pracą wyjścia.

Jeżeli założymy, że na zewnątrz metalu elektron ma potencjał równy zeru i że przestrzenią otaczającą jest próżnia, wówczas praca wyjścia:

W = |e| φ, gdzie e jest ładunkiem elektronu, zaś φ — tzw. potencjałem wyjścia.

Energię wystarczającą na pokonanie pracy wyjścia możemy dostarczyć elektronowi pod postacią energii cieplnej (termoemisja elektronowa), energii kwantu promieniowania (zjawisko fotoelektryczne) oraz podczas niesprężystych zderzeń jonów lub elektronów (wtórna emisja elektronowa, efekt dynatronowy).

KONTAKTOWA RÓŻNICA POTENCJAŁÓW

Jeżeli zetkniemy ze sobą dwa różne metale, to w warstwie przygranicznej po obu stronach styku powstanie nadmiar ładunków przeciwnego znaku. Powstanie w ten sposób skok potencjału, zwany kontaktową różnicą potencjałów lub napięciem kontaktowym.

Istnieją dwie zasadnicze przyczyny powstawania napięcia kontaktowego — różna praca wyjścia elektronów z tych metali i różna gęstość gazu elektronowego.

Niech praca wyjścia z metalu I wynosi W₁ i niech będzie większa od W₂ (pracy wyjścia z metalu II). Gdy ten metale doprowadzimy do zetknięcia, na skutek ruchu cieplnego elektronów nastąpi przejście pewnej ich liczby z metalu I do II i z metalu II do I. Ponieważ praca wyjścia W₂ jest mniejsza niż W₁, w jednostce czasu więcej elektronów przejdzie z metalu II do I niż z metali I do II. W rezultacie warstwa przygraniczna metalu I naładuje się ujemnie do potencjału V₁, zaś metalu II — dodatnio do potencjału V₂. Powstały w ten sposób skok potencjału utrudnia dalszą migrację elektronów i w rezultacie na złączu ustala się stan równowagi dynamicznej. Kontaktowa różnica potencjałów:

Można uszeregować metale w ten sposób, aby każdy następny w szeregu miał większą pracę wyjścia od poprzedniego: W₁ < W₂ < W₃ … Jest to tzw. szereg napięciowy Volty. Leżą w nim w kolejności rosnących prac wyjścia: Al., Zn, Sn, Cd, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd.

Drugą przyczyną powstawania kontaktowej różnicy potencjałów jest różna gęstość gazu elektronowego w obu zetkniętych metalach. (Przez gęstość n gazu elektronowego rozumiemy liczbę elektronów swobodnych w jednostce objętości metalu). Przypuśćmy, że gęstość gazu elektronowego w metalu I wynosi n₁, a w metalu II — n₂, przy czym n₂ > n₁. W takim przypadku liczba elektronów dyfundujących przez złącze w jednostce czasu z metalu II do I jest większa niż z metalu I do II. W związku z tym metal I otrzyma przy złączu ładunek ujemny, a metal II — dodatni. Powstała w ten sposób kontaktowa różnica potencjałów hamuje dalszą dyfuzję elektronów i na złączu ustala się stan równowagi:

gdzie k jest stałą Boltzmanna,

T oznacza temperaturę bezwzględną złącza,

zaś e — ładunek elektronu.

Całkowita kontaktowa różnica potencjałów na złączu dwóch metali wynosi więc:

W zamkniętym obwodzie składającym się z dwóch różnych metali, spojonych ze sobą w dwóch miejscach A i B, jeżeli temperatura obu złączy jest równa, suma spadków potencjału równa się zeru i w takim obwodzie nie może popłynąć prąd. To samo stwierdzenie dla obwodu składającego się z większej liczby metali nosi nazwę prawa Volty.

ZJAWISKO TERMOELEKTRYCZNE

Sytuacja zmienia się zasadniczo, jeżeli w obwodzie zamkniętym, w którym mamy dwa spojenia A i B, temperatura jednego z nich będzie większa. Niech temperatura złącza A będzie równa T₁, a złącza B — T₂, przy czym T₁ >T₂. W tej sytuacji wartości kontaktowych różnic potencjałów na obu złączach nie są już jednakowe co do wartości bezwzględnej i wytwarza się różna od zera różnica potencjałów U_AB między obu spojeniami. Dana jest ona równością:

stąd:

U_AB = c (T₁ - T₂)

gdzie

Zależność ta jest słuszna tylko w pewnym zakresie temperatur. Dla większych różnic T₁ - T₂ zależność różnicy potencjałów U_AB od temperatury już nie jest liniowa.

TERMOOGNIWO

Jeżeli na spojeniach będziemy utrzymywać stałą różnicę temperatur, to w obwodzie będzie istniała stała SEM, zwana siłą termoelektryczną, która spowoduje przepływ prądu termoelektrycznego. Tego rodzaju źródło prądu nazywamy termoelementem albo termoogniwem.

SEM termoogniwa to oczywiście wyliczona powyżej różnica potencjałów U_AB. Jej wartości dla termoogniw są na ogół niewielkie, rzędu miliwoltów, i na ogół rosną ze wzrostem różnicy temperatur. Aby osiągać większe SEM i silniejsze prądy, termoogniwa łączymy szeregowo w termostosy. Termostosy znalazły zastosowanie w przyrządach mierzących natężenia promieniowania np. pieców, lamp, słońca itd. Używamy ich również do pomiarów temperatury — są to wyjątkowo czułe termometry.

ELEMENTY OPTYKI

POLARYZACJA ŚWIATŁA

Fala świetlna jest poprzeczną falą elektromagnetyczną, w której wzajemnie do siebie prostopadłe wektory natężenia pola elektrycznego
i magnetycznego
są równocześnie prostopadłe do kierunku rozchodzenia się fali (czyli do kierunku promienia). W dalszym ciągu, mówiąc o drganiach świetlnych, będziemy mieli na myśli zmiany natężenia pola elektrycznego reprezentowane przez wektor pola elektrycznego
, zwany także wektorem świetlnym — jak się bowiem okazało, przede wszystkim ta składowa fali elektromagnetycznej oddziałuje z materią.

W fali świetlnej, wychodzącej bezpośrednio ze źródła, drgania odbywają się we wszystkich możliwych kierunkach (źródło światła jest bowiem zbiorem zupełnie chaotycznie promieniujących źródeł elementarnych, np. atomów lub cząsteczek), zawsze jednak są prostopadłe do kierunku rozchodzenia się promienia. Światło takie nazywamy naturalnym lub niespolaryzowanym. Sprowadzenie drgań poprzecznej fali świetlnej do jednej płaszczyzny nazywamy polaryzacją fali. Wyróżniamy trzy rodzaje polaryzacji: liniową, kołową i eliptyczną.

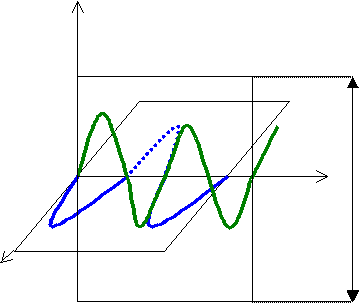
(schematyczne przedstawienie liniowo spolaryzowanej fali świetlnej)

Bardzo rzadko mamy do czynienia ze światłem spolaryzowanym całkowicie, natomiast niezmiernie często ze światłem spolaryzowanym częściowo (będącym mieszaniną światła niespolaryzowanego i spolaryzowanego całkowicie). Charakteryzujemy je przez tzw. stopień polaryzacji wiązki światła. Jest to wielkość procentowa, wyrażana wzorem:

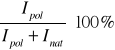
gdzie, jeżeli natężenie fali świetlnej (całkowitą wartość niesionej przez nią energii) opiszemy jako I,

I_pol oznacza część energii przypadającej na światło całkowicie spolaryzowane,

a I_nat — na światło naturalne.

SPOSOBY OTRZYMYWANIA ŚWIATŁA SPOLARYZOWANEGO LINIOWO

Przy najczęściej spotykanej polaryzacji liniowej wektor świetlny
i kierunek promienia r wyznaczają płaszczyznę drgań, zwaną płaszczyzną polaryzacji.

W warunkach naturalnych polaryzacja światła zachodzi najczęściej podczas odbicia od przezroczystych dielektryków, np. wody, szkła, mas plastycznych, lakierów itp., oraz podczas rozpraszania światła (np. światła słonecznego w atmosferze).

1. Polaryzacja przez odbicie i załamanie.

W warunkach laboratoryjnych wiązki światła spolaryzowanego przez odbicie i załamanie otrzymujemy np. w płytkach szklanych.

Wiązka światła niespolaryzowanego polaryzuje się częściowo przy odbiciu lub załamaniu w ośrodku izotropowym. Brewster (1815 r.) wykazał, że gdy tangens kąta padania α jest równy współczynnikowi załamania powierzchni, na którą światło pada, czyli kiedy promień odbity i załamany tworzą ze sobą kąt 90˚, wówczas promień odbity jest całkowicie spolaryzowany. Drgania świetlne odbywają się przy tym w płaszczyźnie prostopadłej do płaszczyzny padanie światła, to znaczy są równoległe do powierzchni odbijającej. Promień załamany jest spolaryzowany częściowo, a drgania odbywają się w płaszczyźnie równoległej do płaszczyzny padania.

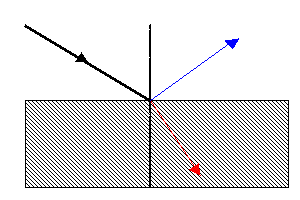
Całkowicie spolaryzowany promień odbity jest zaznaczony na niebiesko,

częściowo spolaryzowany promień załamany — na czerwono.

Promienie załamany i odbity tworzą ze sobą kąt 90˚, a zatem α + β= 90˚.

Warto nadmienić, że energia wiązki padającej dzieli się nierównomiernie między wiązki odbitą i załamaną. Kąt padania α jest nazywany kątem całkowitej polaryzacji lub kątem Brewstera.

2. Polaryzacja przez podwójne załamanie.

Pewne rodzaje ośrodków fizycznych o własnościach anizotropowych (kryształy) wykazują się szczególnym rodzajem właściwości optycznych, zwanym zdolnością podwójnego załamania światła. Środowiska takie nazywamy dwójłomnymi.

Gdy na równoległościenną płytkę, sporządzoną np. ze szpatu islandzkiego (CaCO₃) rzucimy prostopadle promień światła niespolaryzowanego, podzieli się on na dwa promienie, tzn. ulegnie podwójnemu załamaniu. Jeden z promieni, Z (zwyczajny), biegnie prosto, zachowując się zgodnie z prawami załamania światła, drugi zaś, promień N (nadzwyczajny) — nie podlega prawom załamania światła. Okazuje się, że obydwa promienie są całkowicie liniowo spolaryzowane i drgania ich zachodzą w dwóch płaszczyznach do siebie prostopadłych, których kierunek zależny jest od orientacji osi kryształu względem kierunku promienia padającego.

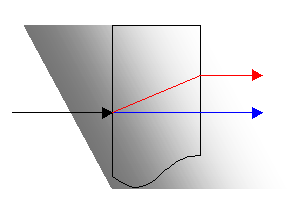
Kolorem niebieskim zaznaczono promień zwyczajny Z, kolorem czerwonym — promień nadzwyczajny N.

W niektórych kryształach istnieje taki kierunek, w którym nie występuje podwójne załamanie — promień padający prostopadle na płytkę wyciętą z kryształu prostopadle do tego kierunku biegnie wewnątrz kryształu i wychodzi z niego jako promień pojedynczy. Tak wyróżniony kierunek w krysztale nazywamy jego główną osią optyczną, a kryształ o tej właściwości zaliczamy do kryształów jednoosiowych (kryształy należące do układów tetragonalnego, heksagonalnego i romboedrycznego). Pozostałe układy krystalograficzne obejmują kryształy dwuosiowe, w których oba promienie są nadzwyczajne.

Każdą płaszczyznę, która przechodzi przez kierunek osi optycznej kryształu i padający promień świetlny nazywamy przecięciem głównym kryształu. Drgania świetlne promienia nadzwyczajnego zachodzą zawsze w przecięciu głównym kryształu, a drgania promienia nadzwyczajnego — w płaszczyźnie prostopadłej do przecięcia głównego.

Fizyczną przyczyną zjawiska dwójłomności jest anizotropia środowiska, jakim jest kryształ dwójłomny. Wyobraźmy sobie, że w takim środowisku rozpoczyna emisję źródło światła umieszczone w jego centrum (punkt O). Powstają wówczas dwie fale świetlne: o powierzchniach kulistej i elipsoidalnej.

Fala o powierzchni kulistej odpowiada fali „zwyczajnej” i we wszystkich kierunkach rozchodzi się z jednakową prędkością (tak, jak w środowisku izotropowym). Fala elipsoidalna odpowiada fali „nadzwyczajnej”, której prędkość w wybranym kierunku OA jest największa (i równa prędkości fali zwyczajnej), a w kierunku OB do niego prostopadłym — najmniejsza. Okazuje się, że kierunek OA jest kierunkiem głównej osi optycznej kryształu.

Wynika z tego, że gdy promień pada na kryształ równolegle do osi optycznej, promień zwyczajny (fala kulista) i nadzwyczajny (fala elipsoidalna) pokrywają się ze sobą, ponieważ w tym kierunku obydwie fale mają taką samą prędkość. Jeżeli natomiast kierunek promienia tworzy z osią optyczną kąt, następuje podwójne załamanie. Promień zwyczajny biegnie z prędkością fali kulistej, a promień nadzwyczajny — z nieco mniejszą prędkością fali elipsoidalnej. Promień nadzwyczajny ma mniejszą prędkość, co odpowiada sytuacji przejścia wiązki światła do środowiska o większym współczynniku załamania — dlatego też załamuje się „od normalnej”, oddzielając się wyraźnie od biegnącego na wprost promienia zwyczajnego.

3. Polaryzacja przy użyciu polaryzatora.

Jest to w gruncie rzeczy polaryzacja światła przez załamanie, ale wykonywana przy pomocy polaryzatora — specjalnego urządzenia, służącym do otrzymywania światła spolaryzowanego. W jego budowie wykorzystuje się zjawisko dwójłomności kryształów (pryzmat Nicola) lub zjawisko dichroizmu (polaroid).

ZAŁAMANIE ŚWIATŁA

Załamanie promienia świetlnego zachodzi, gdy światło pada na granicę dwóch przezroczystych ośrodków, z których każdy ma inną przepuszczalność (tzn. fale świetlne mają w nim inną prędkość).

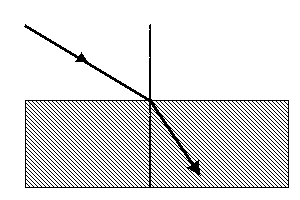
Promień padający pod kątem α do tzw. normalnej padania (umowna linia prostopadła do powierzchni, na którą pada światło) po przejściu granicy ośrodków zmienia kierunek i biegnie pod kątem β.

Kąt β wzrasta ze wzrostem kąta α, kąty te jednak nie są do siebie proporcjonalne. Wprost proporcjonalne są do siebie sinusy kątów α i β.

Iloraz sinusów tych dwóch kątów jest stały dla każdego układu dwóch środowisk. Jest on nazywany względnym współczynnikiem załamania światła n środowiska drugiego względem pierwszego (n_1→2).

Wykazane zostało, że wartość współczynnika n jest zarazem ilorazem prędkości światła w ośrodku pierwszym do prędkości światła w ośrodku drugim. Jest to prawo załamania światła:

Z powyższego zapisu wynika, że:

1. gdy n > 1, to prędkość światła w ośrodku pierwszym jest większa od prędkości światła w ośrodku drugim, czyli ośrodek drugi jest optycznie gęstszy (np. przejście z powietrza do wody). W tym przypadku kąt α jest większy od kąta β. Światło załamuje się do normalnej padania.

2. gdy n < 1, to prędkość światła w ośrodku pierwszym jest mniejsza od prędkości światła w ośrodku drugim, czyli ośrodek drugi jest optycznie rzadszy (np. przejście ze szkła do powietrza). W tym przypadku kąt α jest mniejszy od kąta β. Światło załamuje się od normalnej padania.

Jeżeli środowiskiem pierwszym jest próżnia, a drugim dowolna inna substancja, na której granicę pada światło, współczynnik załamania wynosi:

Dla dowolnej substancji współczynnik n jest w takim przypadku większy od zera, ponieważ w żadnym środowisku światło nie ma prędkości większej niż w próżni. Współczynnik ten nazywamy bezwzględnym współczynnikiem załamania światła.

Na podstawie wartości tego współczynnika możemy przewidzieć zachowanie się promienia na granicy dowolnych dwóch środowisk. Im większy n, tym większa optyczna gęstość środowiska, a zatem przechodząc ze ośrodka o mniejszym n do ośrodka o n większym światło będzie załamywało się do normalnej padania — i odwrotnie.

Względny współczynnik załamania światła n_1→2 na granicy między tymi środowiskami obliczamy ze wzoru:

gdzie n₂ i n₁ są bezwzględnymi współczynnikami załamania światła obu ośrodków.

CAŁKOWITE WEWNĘTRZNE ODBICIE

Całkowite wewnętrzne odbicie światła może zachodzić, kiedy wiązka światła pada na granicę dwóch środowisk, z których pierwsze jest optycznie gęstsze od drugiego (np. promień świetlny przechodzi ze szkła do powietrza).

Wiadomo, że w takim przypadku promienie załamują się od normalnej, czyli kąt β, pod którym światło biegnie po przejściu granicy środowisk, jest większy od kąta α, pod którym biegnie przed załamaniem. Stopniowe zwiększanie wartości kąta α będzie prowadziło do zwiększania się kąta β. Wreszcie dojdziemy do takiej wartości α, dla której wartość kąta będzie wynosiła 90˚, tzn. światło w ogóle nie wyjdzie do ośrodka optycznie rzadszego, lecz po załamaniu pobiegnie wzdłuż granicy. Tę wartość kąta α nazywamy kątem granicznym, a przejście światła padającego na granicę ośrodków pod tym kątem — przejściem granicznym.

Jeżeli teraz promień światła rzucimy na granicę środowisk pod kątem większym od kąta granicznego, promień ulegnie całkowitemu wewnętrznemu odbiciu — nie wyjdzie w ogóle ze środowiska optycznie gęstszego, a jedynie zmieni swój kierunek biegu.

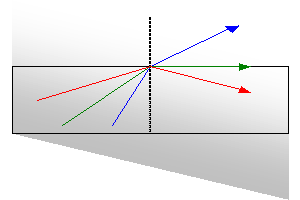
Promień zaznaczony na niebiesko ilustruje przejście światła padającego pod kątem α mniejszym od kąta granicznego.

Promień zaznaczony na zielono — pod kątem α równym kątowi granicznemu.

Promień zaznaczony na czerwono — pod kątem α większym od kąta granicznego.

Oczywiście, zjawisko wewnętrznego odbicia zachodzi również dla wartości α mniejszych od wartości kąta granicznego, jest to jednak odbicie wyłącznie częściowe.

Dla przejścia granicznego prawo załamania przybiera postać:

a ponieważ sin 90˚ = 0, to:

stąd:

Z powyższego wzoru możemy wyliczyć wartość kąta granicznego.

20218/L → 2374505

E_λ,T

T = const

∆R = E∆λ

λ

λ +∆λ

λ

6000˚K

3000˚K

1000˚K

λ

E

r

α

α

β

β

α

powietrze

szkło

---