Ćwiczenie 1

WYPŁYW CIECZY ZE ZBIORNIKA

1. Cel ćwiczenia

Celem ćwiczenia jest doświadczalne wyznaczenie współczynnika wypływu cieczy ze zbiornika oraz porównanie wyników doświadczenia z wynikami rozwiązania teoretycznego.

2. Wprowadzenie

Prędkość wypływu cieczy przez otwór w dnie zbiornika możemy obliczyć z równania Bernoulliego. Dla poziomu zwierciadła cieczy oraz dla przekroju strumienia w otworze wylotowym (rys. 1.1) możemy napisać

(1.1)

Ciśnienie barometryczne na obu poziomach jest praktycznie jednakowe (przy różnicach wysokości, jakie bierzemy pod uwagę, różnice ciśnień nie są uchwytne)

(1.2)

Z kolei z równania ciągłości strugi wynika

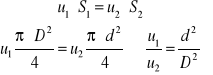
(1.3)

A stąd, wiedząc, że
otrzymujemy

(1.4)

Po takich uproszczeniach równanie Bernoulliego możemy zapisać w postaci

(1.5)

Oznaczając przez
wysokość zwierciadła cieczy ponad poziomem wylotu, otrzymamy wyrażenie pozwalające określić liniową prędkość wypływu

(1.6)

Prędkość ta zależna jest wyłącznie od wysokości H, natomiast kształt zbiornika nie ma na jej wielkość żadnego wpływu.

Objętościowe natężenie wypływu wyniesie więc

(1.7)

gdzie S₂ jest rzeczywistym przekrojem strugi.

W rzeczywistości nie operujemy przekrojem strugi, lecz przekrojem otworu w zbiorniku S - stąd objętościowe natężenie wypływu cieczy rzeczywistej ze zbiornika będzie wyrażać równanie

(1.8)

w którym ϕ jest współczynnikiem poprawkowym zwanym współczynnikiem wypływu, uwzględ­niającym kontrakcję strugi. Wartość jego zależy od kształtu i profilu otworu oraz jego położenia względem ścian zbiornika. Jest on zawsze mniejszy od jedności. Równanie (1.8) stosuje się również dla cieczy rzeczywistych. Współczynnik ϕ zależy wówczas dodatkowo od rodzaju cieczy.

Wykorzystując równanie (1.8) możemy wyprowadzić wzór na czas opróżniania zbiornika.
W różniczkowym czasie dτ wypływa ze zbiornika różniczkowa objętość cieczy

(1.9)

Z drugiej strony objętość ta zgodnie z równaniem (1.7) może być przedstawiona jako

(1.10)

Porównując prawe strony równań (1.9) i (1.10) otrzymamy równanie

(1.11)

z warunkiem początkowym
(1.12)

Całkując równanie (1.11) otrzymamy wyrażenie na czas opróżniania zbiornika

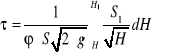
(1.13)

lub czas całkowitego opróżniania zbiornika

(1.13a)

Równania powyższe pozwalają obliczyć czas opróżniania zbiornika pod warunkiem,
że znamy wymiary zbiornika, a więc powierzchnię przekroju wylotu S oraz zależność S₁ = f(H),
a także współczynnik wypływu ϕ. Znając natomiast czas wypływu i wymiary zbiornika, możemy
z równania (1.13) obliczyć współczynnik wypływu ϕ.

Współczynnik wypływu ϕ oblicza się ze zmodyfikowanego równania (1.13)

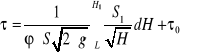
(1.14)

gdzie τ₀ jest czasem opróżniania się końcówki równym w przybliżeniu czasowi swobodnego spadku z wysokości L, który jako znikomo mały w porównaniu z czasem opróżnienia całego zbiornika możemy pominąć.

Całkowania dokonujemy niezależnie dla części cylindrycznej i stożkowej zbiornika (rys. 1.3), tak więc

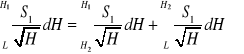
(1.15)

W części cylindrycznej zbiornika powierzchnia przekroju jest stała i wynosi

(1.16)

stąd

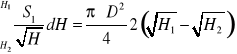
(1.17)

W części stożkowej powierzchnia dowolnego przekroju poziomego odległego o wartość H od wylotu końcówki, a o wartość x od wierzchołka stożka (rys. 1.4) wynosi

(1.18)

Z kolei

(1.19)

(1.20)

zatem

(1.21)

Drugi składnik równania (1.14) w wyniku zastosowania powyższej zależności wyniesie

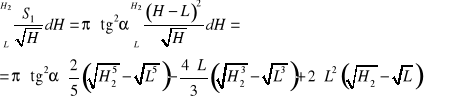
(1.22)

Uwzględniając zależności (1.17) i (1.22) w równaniu (1.14) otrzymujemy wzór na czas opróżniania się zbiornika

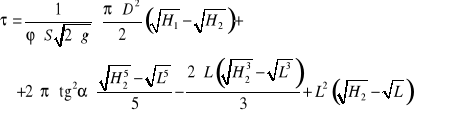
(1.23)

Z powyższego wzoru możemy obliczyć wartość współczynnika wypływu ϕ, jeśli znamy wymiary zbiornika (S, D, H₁, H₂, L) oraz czas opróżniania τ.

W przypadku zbiornika bez końcówki (L = 0) równanie (1.23) upraszcza się do postaci

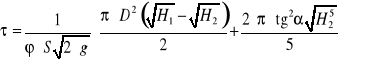
(1.24)

3

---