Dariusz Badura

Diagnostyka i niezawodność systemów komputerowych

Wykład

Wykład 1

DIAGNOSTYKA, BEZPIECZEŃSTWO I NIEZAWODNOŚĆ SPRZĘTU KOMPUTEROWEGO

1. Wprowadzenie

wiarygodności systemów (ang. dependability) obejmuje następującą problematykę

• dyspozycyjności i diagnostyki,

• niezawodności

• bezpieczeństwa oraz

• zabezpieczenia.

Podczas projektowania systemów podejmowane są zabiegi o to, by:

• systemy działały: niezawodność

• systemy były wykorzystywane i dostępne w sposób regularny: dyspozycyjność

• w zastosowaniach krytycznych nie powodowały katastrof: bezpieczeństwo

• uniemożliwić dostęp do danych oraz manipulowania tymi danymi zabezpieczenie

• o dyspozycyjności i bezpieczeństwie systemów można mówić wtedy, gdy istnieją środki zapewniające diagnostykę systemu w celu eliminacji uszkodzeń lub ich skutków.

• Relacje pomiędzy niezawodnością, dyspozycyjnością, bezpieczeństwem i zabezpieczeniem systemów są złożone różną od prostej podległości.

• Odpowiednie zaprojektowanie systemu może znacznie podnieść poziom diagnostyczny i bezpieczeństwa; prowadzi to do wzrostu złożoności układu, a przez to do obniżenia niezawodności.

• Trudno rozdzielać pojęcia niezawodności, diagnostyki i bezpieczeństwa elementów składowych systemu: sprzętu i oprogramowania. Szereg fukcji również w zakresie zapewnienia odpowiedniego poziomu diagnostyki i bezpieczeństwa może pełnić wymiennie sprzęt i oprogramowanie.

2. Wiarygodność jako najistotniejsza właściwość systemów komputerowych

Wiarygodność definiuje się jako działania sytemu komputerowego, która pozwala mieć uzasadnione zaufanie do usług, które ten system dostarcza - postrzegane przez użytkownika systemu.

Rozróżnia się cztery atrybuty wiarygodności:

• dyspozycyjność,

• niezawodność,

• bezpieczność,

• zabezpieczenie.

Dyspozycyjność systemu rozumiana jest jako gotowość do użycia, a zatem jest miarą zdolności systemu do wypełniania usług zgodnych ze specyfikacją w sposób regularny.

Wiarygodny w tym przypadku znaczy dyspozycyjny.

W pewien sposób można kojarzyć dyspozycyjność z efektywnością, jednak tylko w tym zakresie, w którym określa się właściwość zdolności systemu do jego łatwej i szybkiej konserwacji. Dyspozycyjność może być mierzona czasem niedostępności systemu wynikającej z realizacji zadań serwisowych, a to nierozerwalnie wiąże się ze zdolnościami diagnostycznymi systemu: łatwością wykrywania, lokalizacji i usuwania uszkodzeń w systemie.

Niezawodność rozumiana jest jako ciągłość usług i określana jest jako właściwość systemu określona przez prawdopodobieństwo spełniania przez system postawionych mu wymagań w określonym czasie i w określonych warunkach.

Z punktu widzenia miary

Niezawodność systemu jest to prawdopodobieństwo zdarzenia polegającego na tym, że w z góry zadanym przedziale czasowym, przy określonych warunkach, system wykona zadanie do którego został przeznaczony. O niezawodności systemu komputerowego decydują jego składowe, w ogólnym przypadku sprzęt i oprogramowanie. Uszkodzenia sprzętu powstają zazwyczaj w trakcie jego użytkowania, a dzisiejsze technologie zapewniają bardzo wysoką niezawodność sprzętu w stosunku do jeszcze niedawno uzyskiwanej. Inaczej się ma z niezawodnością oprogramowania. Uszkodzenia w oprogramowaniu powstają w czasie jego powstawania.

Wiarygodny w tym przypadku znaczy niezawodny,

Nasze rozważania ograniczone są tematycznie jedynie do tych dwóch atrybutów. Pozostałe dwa można scharakteryzować następująco.

Bezpieczność rozumiana jest jako zdolność do uniknięcie katastrofalnych konsekwencji dla środowiska. wiarygodny znaczy bezpieczny,

Zabezpieczenie rozumiane jest jako zapobieganie nieupoważnionemu dostępowi do danych i / lub manipulowanie danymi; wiarygodny znaczy zabezpieczony

Dyspozycyjność i niezawodność są zawsze wymagane, chaciaż ich stopień zależy od zastosowania.

Bezpieczeństwo a niezawodność systemów komputerowych.

Pojawiający się uszkodzenie powinno zatem spowodować jedną z dwóch reakcji systemu bezpiecznego:

- przejście w stan bezpieczny z jednoczesną sygnalizacją wystąpienia uszkodzenia, lub

- zamaskowanie błędu lub defektu poprzez nadmiar w układzie (systemie).

Niezawodność określana jest jako właściwość systemu określona przez prawdopodobieństwo spełniania przez system postawionych mu wymagań w określonym czasie i w określonych warunkach.

Bezpieczeństwo określa właściwość systemu określona przez prawdopodobieństwo spełniania przez system postawionych mu wymagań lub przejścia systemu w stan nie powodujący lub nie prowadzący pośrednio do katastrofy.

W systemach komputerowych rozdziela się pojęcie niezawodności samego sprzętu od niezawodności oprogramowania.

Naruszenie wiarygodności

Defekt sytemu występuje wtedy gdy dostarczona usługa przestaje być zgodna ze specyfikacją, która oznacza uzgodniony opis oczekiwanych funkcji i / lub usług systemu.

Błąd jest to część stanu sytemu, która jest odpowiedzialna za będący jego następstwem defekt: błąd mający wpływ na usługę systemu jest symptomem defektu, który właśnie lub wcześniej wystąpił.

Uszkodzenie jest to stwierdzona lub hipotetyczna przyczyna wystąpienia błędu.Zależności pomiędzy tymi pojęciami pokazuje rysunek 1.

Przykład fizycznego uszkodzenia, => błędu, => defektu

Środki zapewniające wiarygodność:

a) zapobieganie uszkodzeniom: jak zapobiegać wystąpieniu lub wprowadzeniu uszkodzeń

b) tolerowanie uszkodzeń: jak zapewnić usługę zgodną ze specyfikacją, niezależnie od uszkodzeń

c) usuwanie uszkodzeń: jak ograniczyć obecność uszkodzeń

d) prognozowanie uszkodzeń: jak oszacować aktualną liczbę, możliwość przyszłego wystąpienia oraz konsekwencje uszkodzeń

• Zapobieganie uszkodzeniom i tolerownie uszkodzeń można traktować jako metody dostarczania wiarygodności, tzn. określające jak wyposażyć system w zdolność dostarczania usługi zgodnie ze specyfikacją.

• Usuwanie i przewidywanie uszkodzeń można traktować jako metody walidacji wiarygodności, tzn. określające jak osiągnąć zaufanie do zdolności systemu do dostarczania usługi zgodnie ze specyfikacją.

• Zaufanie do usługi systemu i uzasadnienie tego zaufania są oparte na ocenie systemu, przeprowadzonej głównie ze względu na te atrybuty wiarygodności, które odnoszą się do usługi systemu.

Diagnostyka naruszenia wiarygodności

Uszkodzenia

Natura uszkodzeń :

- uszkodzenia przypadkowe,

- uszkodzenia umyślne, (celowo, przypuszczalnie złośliwie).

Żródła:

-przyczyny fenomenologiczne

-uszkodzenia fizyczne,

-uszkodzenia spowodowane przez człowieka

-granice systemu

-uszkodzenia wewnętrzne,

-uszkodzenia zewnętrzne,

-faza powstania w odniesieniu do życia systemu

-uszkodzenie projektowe,

-uszkodzenia operacyjne.

Trwałość w czasie:

-uszkodzenia trwałe,

-uszkodzenia przemijające.

Błędy

Błąd jest abstrakcyjnym zjawiskiem odpowiedzialnym za defekt, zależnym od:

- budowy sytemu, a więc typu istniejącej redundancji:

- redundancja zamierzona,

- redundancja niezamierzona,

• działania systemu;

• definicji defektu z aspektu użytkownika;

Defekty

Kryteria:

- dziedzina,

- percepcja przez użytkowników systemu i

- konsekwencje dla otoczenia.

Kryterium dziedziny defektu pozwala wyróżnić:

-defekty wartości: wartość dostarczonej usługi jest niezgodna ze specyfikacją

-defekty synchronizacji czas dostarczonej usługi jest niezgodny ze specyfikacją.

Kryterium percepcji defektu wyróżnia:

-defekty zgodne, tzn. wszyscy użytkownicy systemu mają taką samą percepcję defektu

-defekty niezgodne, tzn. użytkownicy systemu mają różne percepcje danego defektu; defekty niezgodne nazywane są defektami bizantyjskimi.

Konsekwencje defektów dla otoczenia systemu:

- defekty łagodne, których konsekwencje są tego samego rzędu wielkości, co korzyści wynikające z dostarczanej usługi przy braku defektu;

- defekty katastroficzne, których konsekwencje są nieporównywalnie większe niż korzyści wynikające z dostarczanej usługi przy braku defektu.

Krytyczność systemu jest to najwyższa dotkliwość jego możliwych typów defektów.

Wykład 2

3. Diagnostyka układów i systemów cyfrowych

Etapy życia urządzenia:

• projektowanie,

• produkcja

• eksploatacja.

Typy procesów diagnostycznych:

• diagnostyka on-line obejmująca testowanie i wykrywanie uszkodzeń podczas normalnej pracy urządzeń

- systemy głosujące,

- kody detekcyjno-korekcyjne np. w układach sprawdzających poprawność transmisji i układy kontroli zapisu i odczytu do/z pamięci. Tzw. Samosprawdzanie (ang. self-checking).

• pseudo on-line (wykradanie luk czasowych).

• diagnostyka off-line odnosząca się do testowania i wykrywania uszkodzeń w urządzeniach nie wykonujących w czasie wykonywania procesu diagnostycznego swych podstawowych zadań.

Proces diagnostyczny:

- test wykrywający ewentualne uszkodzenia, i jeśli takie wystąpi,

- zlokalizowanie jego wystąpienie oraz

- dokonanie naprawy.

Ze względu na architekturę systemu testującego:

- testowanie zewnętrzne,

- testowanie wewnątrz-układowe,

- testowanie programowe.

Wykrywanie uszkodzeń w układach cyfrowych

Podczas testowania układu cyfrowego (CUT - ang. Circuit Under Test) z generatora pobudzeń testowych (TPG - ang. Test Pattern Generator) podawane są na wejścia pierwotne układu pobudzenia testowe. Pobudzenia testowe są wektorami wejściowymi, dla których sprawny układ podaje na wyjścia pierwotne stany różne od stanów podawanych na wyjścia przez układ uszkodzony.

Niemożliwe jest rozpatrywanie wszystkich możliwych uszkodzeń. Dlategoteż, dla rozpatrywanego układu zakłada się skończony zbiór uszkodzeń.

wektor V - wektor wejść pierwotnych układu

wektor Z - wektor wyjść pierwotnych układu

Poszukiwania sekwencji testującej układ cyfrowy

• wyznaczanie wzorów testowych

• weryfikacja pobudzeń testowych

• minimalizacja pobudzeń testowych

Układy kombinacyjne

• test posiada charakter kombinacyjny, tzn. kolejność pobudzeń testowych nie ma znaczenia

• oddzielnym problemem testy dla uszkodzeń zmieniających układ kombinacyjny w asynchroniczny sekwencyjny układ cyfrowy (np. zwarcie linii)

Układy sekwencyjne

• test wykrywający jedno uszkodzenie może mieć charakter sekwencji, która dzieli się na sekwencję pobudzającą i sekwencję wyprowadzającą.

• sekwencja pobudzająca pobudza uszkodzenie i przesyła je na jedno z wyjść układu sekwencyjnego - może to być wyjście stanu wewnętrznego, niedostępne (nie będące wyjściem pierwotnym układu

• sekwencja wyprowadzająca powoduje przesłanie sygnału błędu na jedno z wyjść pierwotnych układu

Wykład 3.

D-algorytm

1. Wyznaczanie testów detekcyjnych algorytmem D.

W D - algorytmie uszkodzenie oznaczane jest symbolem D, przyjmującym w układzie sprawnym wartość 1, a w układzie uszkodzonym 0. Analogicznie ~D przyjmuje w układzie sprawnym 0, a w układzie uszkodzonym 1.

Procedura wyznaczania testów obejmuje dwa etapy:

1. wyznaczanie pierwotnego pobudzenia uszkodzenia (D-pobudzenie) i przesłania wartości błędu na wybrane wyjście - tzw. D-sterowanie;

2. uzgodnienie warunków przesłania wartości błędu przez kolejne elementy układu - tzw. operacja zgodności.

Etap pierwszy w pierwszej części dotyczy przypisania, w zależności od typu uszkodzenia, symbolu D lub ~D (rys. 1). Następnie wartość D (~D) przesyłana jest na wybrane wyjście. Ponieważ zgodnie z wcześniej opisaną zasadą symbole D i ~D reprezentują wartości logiczne sprawnego i uszkodzonego układu, tworzą zatem wraz z wartościami 0 i 1 algebrę, zwaną często D-algebrą. Przesyłając wartości D i ~D na wyjście układu należy zapewnić propagację wartości reprezentującej błąd poprzez zadanie odpowiednich wartości na pozostałych wejściach bramek, poprzez które propaguje wartość D lub ~D.

Rys. 1. Operacje D-pobudzenia i przesłania

Etap drugi polega na sprawdzaniu i uzgadnianiu na pozostałych elementach warunków przenoszenia sygnału błędu na wybrane wyjście układu. Zasady uzgadniania wyjaśnimy na przykładzie. Na rysunku 2 przedstawiono jednowyjściowy układ kombinacyjny złożony z 6 bramek. Na schemacie zaznaczono miejsce uszkodzenia typu s-z-0 D-pobudzenie oraz D-przesłanie z wyróżnionymi warunkami przesłania.

Rys. 2. Proces D-sterowania dla przykładowego układu kombinacyjnego

Na rys. 3 zaprezentowano operację D-uzgodnienia oraz jej wynik.

Rys. 3. Proces D-uzgadniania dla przykładowego układu kombinacyjnego

Przykład uszkodzenia wielokrotnego

Rozpatrzmy uszkodzenie wielokrotne:

x2: s-z-1, x3: s-z-1, x4: s-z-1

Rys 4. Przykładowy układ kombinacyjny

przedstawionym na rys 4. W procesie wyznaczania testów D-algorytmem zostanie zapoczątkowany każdy z 7 możliwych procesów D-sterowania, dla każdego niepustego podzbioru zbioru ścieżek. Jedynie 4 spośród nich dają wynik pozytywny.

Liczba inicjowanych procesów D-sterowania znacznie wzrasta dla układów o złożonej strukturze (duża liczba bramek, rozgałęzień) oraz dla uszkodzeń wielokrotnych w tych układach. Istnieje prosty sposób znacznego ograniczenia tej liczby, bez straty ogólności algorytmu.

Warunkiem propagacji sygnału D (~D) przez n-wejściowy funktor AND lub NAND jest wartość 1 lub D (~D) na pozostałych wejściach funktora. Ta właściwość umożliwia wprowadzenie uproszczonego zapisu warunków D-propagacji zilustrowanego w tablicy 1.

Tablica 1.

Postać pełna

Postać uproszczona

x1

x2

...

Xn-1

Xn

FAND

x1

x2

...

xn-1

xn

FAND

1

1

1

D

D

1+

1+

1+

D

D

1

1

D

D

D

:

:

:

:

:

Gdzie 1+ = { 1 , D }

D

1

1

D

D

D

1

D

D

D

:

:

:

:

:

D

D

D

D

D

Transmisja D z wejścia xn na wyjście fAND

Określenie warunków D propagacji w tej postaci pozwala ograniczyć procesy D-sterowania jedynie do transmisji “D-informacji” pojedynczymi ścieżkami układu .

Opisane wyżej ulepszenie D-algorytmu wymaga jednak rozszerzenia alfabetu i zdefiniowania elementarnych funkcji bulowskich dla elementów tego alfabetu. Symbole rozszerzonego alfabetu Vr zdefiniowano w oparciu o wprowadzone przez Roth'a symbole alfabetu V = {0, 1, D, ~D, u, e} , w następujący sposób

Vr = { 0r, 1r, Dr, ~Dr, 0+r, 0-r, 1+r, 1-r, ur, er }

0r = {0} , 1r = {1}, Dr = {D}, ~Dr = {~D}, 0+r = {0, D}, 0-r = {0, ~D},

1+r = {1, D}, 1-r = {1, ~D}, ur = {0, 1, D, ~D}, er = {},

Natomiast funkcje dla elementów rozszerzonego alfabetu zdefiniowano następująco:

FVr( a1,...,an,...,aN ) = {fV(b1i,...,bni,...,bNi), bni  an}

W tablicy 2 opisano D-sześciany pokrycia osobliwego, pierwotnego D-pobudzenia i przesyłowego D-pobudzenia dla funktora AND w rozszerzonym alfabecie. Indeks r został pominięty.

Tablica 2a Pokrycie osobliwe Tablica 2b Pierwotne D-pobudzenie

X1	X2		fAND			X1		X2	fAND
1-	1-		1-			1+		1+	D
1+	1+		1+			0-		U	~D
0-	u		0-			u		0-	~D
U	0-		0-
0+	u		0+
U	0+		0+
				Tablica 2c			Przesyłowe D-pobudzenie
						x1		X2	FAND
						1+		D	D
						D		1+	D
						1-		~D	~D
						~D		1-	~D

Wykład 4.

Projektowanie upraszczające testowanie

Wprowadzenie do układu elementów nadmiarowych zwiększających jego testowalność jest zwane projektowaniem ułatwiającym testowanie (ang. design for testability).

W pracy [ ] podano podstawowe wytyczne dotyczące środków upraszczających testowanie. Wśród nich wymienia się następujące zalecenia co do środków strukturalnych, których wprowadzenie należy uwzględnić podczas projektowania:

• zastosowanie dodatkowych punktów sterowania i obserwowania;

• podział dużych układów na małe podukłady (umożliwiający redukcję wysiłku przy wyznaczaniu testu), a także oddzielenie części analogowej od części cyfrowej;

• zapewnienie układom pamiętającym .łatwej inicjalizacji;

• wprowadzenie możliwości przerwania ścieżek sprzężenia zwrotnego;

• użycie jak najprostszych lub standardowych interfejsów pomiarowych testera, co zapewnia jego dużą uniwersalność

1. Problem sterowalności i obserwowalności układu cyfrowego

Zdolność do wyznaczania i aplikacji testu w dużym stopniu jest zależna od prostoty układu lub inaczej - od bycia zdolnym do sterowania i obserwowania stanów wewnętrznych punktów (węzłów) układu. W praktyce nie można tego uczynić dla znacznej liczby punktów, lecz są już różne techniki polepszające charakterystyki obserwowalności i sterowalności układu.

Dowolny punkt jest sterowalny wtedy, gdy tester potrafi w prosty sposób sterować warością w danym punkcie układu na dowolny poziom logiczny (0, 1 lub wysoka impedancja). Podobnie określa się obserwowalność: punkt układu jest obserwowalny wtedy, gdy tester potrafi w prosty sposób obserwować poprawność wartości w danym punkcie.

Przykładami kluczowych punktów sterowalnych w układach logicznych są [ , ]:

• zegar, wejścia zerowania takich układów jak przerzutniki, liczniki i rejestry szeregowe,

• wejścia selekcji danych (ang. DATA Select) do multiplekserów i demultiplekserów,

• wejścia zezwolenia/zatrzymania (ang. ENABLE/HOLD) mikroprocesorów,

• linie sterowania tzw. trzecim stanem układów z wyjściem trójstanowym,

• wejścia zezwolenia i czytaj/pisz (ang. Read/Write) układów pamięci,

• wejścia: adresowe, danych i sterujące magistrali.

Przykładami kluczowych punktów obserwujących, zwanych również punktami testowania, w układzie logicznym są [ , ]:

• dowolna, bezpośrednio niedostępna linia sterująca, tak jak te wymienione powyżej,

• wyjścia układów pamiętających, takich jak: przerzutniki, liczniki, rejestry szeregowe,

• wyjścia układów „data funnneling”, takich jak: generatory parzystości, kodery priorytetów i multipleksery,

• węzły dowolnej logicznej redundancji,

• sekcje linii głównej o wysokiej obciążalności,

• ścieżki podstawowych (globalnych) linii sprzężeń zwrotnych.

Identyfikacja kluczowych punktów sterowania i obserwowania może być dokonana albo przez wykorzystanie przedstawionych poprzednio list kluczowych punktów testowalnych i obserwujących lub przez analizę testowalności, na przykłąd za pomocą programów CAMELOT i TMEAS, albo przez ich połączenie. Podstawowe miary testowalności to: uśrednione miary probabilistyczne [ , ] oraz przybliżone miary minimalne [ ].

Najprostszym sposobem zwiększania testowalności układu (pakietu) jest zatem wprowadzenie dodatkowych punktów sterujących i obserwujących. Początkowe kluczowe punkty są znane. Następnym krokiem jest modyfikacja bazowego projektu w celu zwiększenia właściwości obserwowania i sterowania. Metody wprowadzania dodatkowych punktów testowania przedstawiono w pracy [ ].

2. Podział na makrobloki

Zalecenie podziału dużych układów na podukłady jest podstawą do rozwijania strukturalnej metody upraszczania testowania polegającej na podziale dużych układów na podukłady - tzw. makrobloki (ang. macros).

Podział na makrobloki wynika z następujących przesłanek intuicyjnych zwanych heurystycznymi:

• W algorytmach automatycznej generacji testów istnieją ograniczenia dotyczące wielkości rozpatrywanych układów.

• Model uszkodzeń powinien być dostosowany do specyfikacji struktury układu.

• O strategii testowania decyduje między innymi liczba sygnałów zegarowych wykorzystywanych w układzie.

• Sterowalność i obserwowalność w znacznym stopniu zależy od wielkości i struktury testowanego układu.

• Realizacja testowania (wykonanie testu) musi być zgodna z architekturą ukłądu.

• Podczas projektowania o podziale układu decyduje hierarchia układu (systemu) wprowadzona przez projektanta.

System cyfrowy na ogół jest podzielony na pakiety układów cyfrowych (ang. Printed Circuit Boards). Na potrzeby testowania punkty połączeń między-pakietowych można wyprowadzić na zewnątrz systemu, wtedy dalszym podziałem będzie separacja układów zamontowanych na jednym pakiecie, umożliwiająca logiczne rozłączenie poszczególnych makrobloków. Podczas podziału na makrobloki powinny być spełnione następujące wymagania:

• każdy makroblok musi być testowany niezależnie,

• każdy makroblok musi być dostępny (sterowalny i obserwowalny) z zewnętrznych łącz pakietu,

• każdy makroblok powinien dotyczyć tego samego typu testów (logika kombinacyjna, RAM, ROM itp.),

• dowolny makroblok powinien być rozłączny z każdym innym,

• makroblok może zawierać dowolną liczbę bloków funkcjonalnych i odwrotnie.

Dwa pierwsze wymagania wiążą się z koniecznością wprowadzenia na pakiet testowych elementów sprzęgających (TES, ang. Test Interface Element), które mają następujące cechy:

• element TES ma być „przezroczysty” w czasie normalnej pracy układu, oraz

• umożliwiać w trybie testowania zarówno równoległy, jak i szeregowy dostęp do układu.

Kolejne etapy wprowadzania cech testowalności do projektu układu cyfrowego, zgodnie z przedstawionymi wymaganiami, zilustrowano na rysunku.

Jeżeli makrobloki są testowane równolegle, to mogą wystąpić dwa rodzaje sprzeczności testowania równoległego. W pierwszym przypadku istnieją wejścia układu scalonego lub pakietu zasilające więcej niż jeden makroblok. Pobudzenia testowe podawane na poszczególne makrobloki będą wtedy zależne, uniemożliwiając tym samym równoległe i niezależne podawanie testów na wejścia makrobloków. W drugim przypadku istnieją niezależne wyjścia makrobloku zbiegające się do jednego wyjścia pakietu lub układu scalonego. W niezależnym testowaniu makrobloków zbieganie się niezależnych wyjść może prowadzić do sprzeczności pojawiających się na nich sygnałów. Aby uniknąć tych sprzeczności, elementy TES powinny być dostępne na obu wejściach każdego sygnału między makroblokami. Jednak nadmiar powierzchni w tym rozwiązaniu będzie duży. A zatem, by zmniejszyć nadmierny koszt zarówno elementów TES, jak i wyprowadzeń sygnałów wejścia/wyjścia niezbędnych do sterowania nimi, elementy TES umieszcza się tylko na każdym wyjściu makrobloku, a bloki testowane są jeden po drugim. W czasie testowania układu podzielonego na makrobloki można osiągnąć 100% pokrycie uszkodzeń wobec ograniczonej liczby zastosowanych pobudzeń testowych.

2. Ścieżka sterująco-obserująca

W celu osiągnięcia łatwej testowalności zaleca się między innymi zapewnienie elementom pamięciowym łatwej ich inicjalizacji (zerowania i ustawiania), a także wprowadzenie możliwości przerwania ścieżek sprzężenia zwrotnego. Jeżeli wejścia wszystkich elementów pamięciowych można wysterować do dowolnej wartości logicznej, a ich wyjścia obserwować bez żądnych ograniczeń, to zadanie testowania układu sprowadza się do testowania jego części kombinacyjnej. Aby zapewnić tę właściwość układu, zaproponowano rozwiązanie z użyciem dodatkowego sygnału sterującego. W zależności od jego stanu układ działa normalnie lub w czasie testowania przekształca się w układ kombinacyjny połączony z jednym lub kilkoma rejestrami przesuwnymi. Rejestr taki łączący w szereg wszystkie elementy pamięci układu będzie zwany dalej ścieżką sterująco-obserwującą (ang. scan-chain lub scan-path).

Kilka firm przedstawiło konkretne rozwiązania układowe, jak na przykład:

• firma IBM zastosowała w swych układach rozwiązania typu LSSD (ang. Level Sensitive Scan Design) - opis pracy rejestru oraz jego konstrukcyjnych odmian można znaleźć w [ ].

• Firma Nippon Electric Co. LtD. Zastosowała rozwiązanie zwane „ścieżką badającą” (ang. Scan-Path) - schemat i szczegóły opisano w [ ],

• Firma Sperry-Univac zaproponowała rozwiązanie typu „badaj/ustaw” (ang. scan/set),

• Firma Fuitsu opracowała rozwiązanie opisane skrótem RAS (ang. Random Access scan).

Wymienione rozwiązania polepszają testowalność układów zawierających elementy pamięci, a w rezultacie następuje średnio kilkunastoprocentowy wzrost rozmiaru układu (ang. overhead). Jednak w konkretnych zastosowaniach część nadmiarowej logiki może być wykorzystana do realizacji zadań użytkowych układu.

Definicje:

Ścieżka sterująco-obserwująca - rejestr szeregowy utworzony z przerzutników - komórek powiązanych z punktami trudno testowalnymi układu. Do tego łańcucha przerzutników włączane są zazwyczaj komórki przerzutników wewnętrznych układu.

Brzegowa ścieżka sterująco-obserwująca - rejestr szeregowy utworzony z komórek (przerzutników) powiązanych z wejściami pierwotnymi i wyjściami pierwotnymi układu. Zazwyczaj zapewniona jest możliwość połączenia szeregowego z ścieżką sterująco-obserwującą i przerzutnikami wewnętrznymi układu.

Wejścia i wyjścia zewnętrzne pakietu lub układu scalonego nazywa się wejściami i wyjściami pierwotnymi.

Logikę układu scalonego lub pakietu można podzielić na dwie kategorie: logikę wewnętrzną i logikę zewnętrzną.

Logika, której wejścia są zasilane przez ścieżkę sterująco-obserwującą, nazywamy logiką wewnętrzną.

Kombinacyjny układ logiczny, którego wejścia są zasilane przez wejścia pierwotne układu scalonego (pakietu) i/lub którego wyjścia zasilają wyjścia pierwotne układu, określa się logiką zewnętrzną.

Jeżeli wszystkie pierwotne wejścia i wyjścia są umieszczone w łańcuchu ścieżki sterująco-obserwującej, to w układzie scalonym lub na pakiecie nie występuje logika zewnętrzna. Taka ścieżka sterująco-obserwująca łącząca wszystkie pierwotne wejścia i wyjścia jest zwana brzegową ścieżką sterująco-obserwującą (ang. Boundary scan-path). W poniższej tabeli przedstawiono trzy strukturalne metody testowania oparte na ścieżce sterująco-obserwującej, wymieniając ich zalety i wady.

Strukturalne metody testowania

Metody testowania	Opis	Dodatek układowy	Efektywność	Wymagania
Metoda 1: Badaj i separuj logicznie	Separacja logiczna nie-testowalnych elementów; dla pozostałej części: technika ścieżki sterująco-obserwującej na pozio-mie pakietu	Dodatkowe układy na pakiecie (multipleksery, sygnały sterujące i taktujące)	Test strukturalny dla części testowalnej techniką ścieżki sterująco-obserwującej, test funkcjonalny lub wewnątrzukła-dowy dla pozostałej części pakietu	Żadne dla elementów katalogowych; ścieżka sterująco-obserwująca dla elementów dedykowanych
Metoda 2: Łańcuch ścieżek sterująco-obserwują-cych	Pakiet testowalny techniką ścieżki sterująco-obserwującej poprzez dodatkowe, funkcyjnie niezależne wyprowadzenia testowe układów scalonych.	Układy na pakiecie (dodatkowe wyprowadzenia i połączenia)	100% test strukturalny pakietu	Wszystkie elementy testowalne techniką ścieżki sterująco-obserwującej z wyprowadzeniami testowymi niezależnymi funkcyjnie; zbiory pobudzeń testowych i informacja o sposobie ich uaktywnienia jest dostępna dla projektanta
Metoda 3: Brzegowa ścieżka sterująco-obserwująca	Test produkcyjny: pełny test połączeń i pobieżny test logiki wewnętrznej; test serwisowy: preferowane obszerne testowanie logiki wewnętrznej elementów za pomocą samotestowania	Brzegowa ścieżka sterująco-obserwująca	100% test strukturalny pakietu	Brzegowa ścieżka sterująco-obserwująca dla elementów katalogowych oraz brzegowa ścieżka sterująco-obserwująca i samotestowanie dla elementów niekatalogowych

Diagnostyka sprzętu: projektowanie, uruchamianie i serwis systemów

• projektowanie układów łatwotestowalnych (ang. design for testability - DFT),

• zasada hierarchicznego testowania systemów cyfrowych

Realizacja ścieżki sterująco-obserwującej:

(poniższe rysunki są zaczerpnięte ze standardu IEEE 1149.1 jak również z innej literatury omawiającej ten standard)

Technika LSSD (ang. Level Sensitive Scan Design)

D - wejściowa linia danych, C - sygnał zegara

L1 - wyjście, I, A, B, L2 - linie kształtujące szeregowe przesyłanie (I - wejście przesuwania danych, L2 - wyjście przesuwania danych, A,B - sygnały dwóch faz przesuwania)

Aplikacja technologii LSSD

Technologia RAS (ang. Random Access Scan)

Brzegowa ścieżka sterująco - obserwująca

• składa się z rejestru „skanującego” dołączonego do wejść i wyjść pierwotnych

• pozwala na efektywne testowanie na poziomie pakietu

• do testowania połączeń na poziomie pakietu

• do izolacji i testowania układów scalonych poprzez układy samo-testujące lub poprzez zastosowanie testu z wykorzystaniem magistrali testującej

• wymaga dodatkowych czterech linii (portów) układu scalonego - Test Access Port (TAP)

• TCK - sygnał zegara

• TMS - sygnał trybu testowania

• TDI - szeregowe wejście danych testowych

• TDO - szeregowe wyjście danych testowych

• wymaga dodatkowej logiki do sterowania procesem testowania - TAP controller

Tryby pracy komórek ścieżki brzegowej

Tryb normalny: Mode_control = `0'

• Dane przesuwane są z IN do OUT

Tryb „skanowania”: ShiftDR = `1', ClockDR = scan clock

• Dane szeregowe przesuwane są z SIN na wyjście SOUT

Tryb „wychwytywania”: ShiftDR = `0', ClockDR = 1 clock pulse

• Dane z wejścia IN wpisywane są do Q_A

Tryb „uaktualniania danej”: z wcześniej ustawioną wartością Q_A , Mode_Control = `1', UpdateDR = 1 clock pulse

• wartość z Q_A wyprowadzana jest na wyjście OUT

Komórka brzegowej ścieżki sterująco - obserwującej

Rysunek przedstawia podstawową strukturę komórki brzegowej ścieżki sterująco-obserwującej. W konkretnych rozwiązaniach komórka ta może być modyfikowana. Komórka taka jest dołączana do każdej linii wejściowej/wyjściowej (I/O port) układu scalonego. Przyczyną popularności ścieżki brzegowej jest jej relatywnie niski koszt umiejscowienia komórek połączonych z wejściami/wyjściami w porównaniu z kosztem wstawienia pełnej ścieżki sterująco-obserwującej.

Architektura brzegowej ścieżki sterująco - obserwującej w układzie scalonym

Płyta drukowana z ścieżką sterująco - obserwującą

Jeżeli na płycie drukowanej z brzegową ścieżką sterująco obserwującą każdy z układów scalonych posiada przerzutniki „skanujące”, mogą one zostać połączone w jeden długi łańcuch skanujący. Jeżeli płyta drukowana zawiera jakieś układy pozbawione logiki „skanującej”, użycie „skanowania” w testowaniu jest nadal możliwe, gdyż te układy mogą być testowane poprzez ścieżkę brzegową jeżeli są nią otaczane.

Tryby pracy ścieżki sterująco - obserwującej

Tryb testowania zewnętrznego (test połączeń)

Przerzutniki “skanujące” pobierają dane (the update mode) a po zadaniu testu i wpisaniu do przerzutników wyniku są przesuwane szeregowo do wyjścia łańcucha.

Tryb testowania wewnętrznego

Podobnie jak w teście połączeń dane w rejestrze ścieżki zadają test i ścieżka zostaje uaktualniona danymi wyników testu. Następnie dane zostają wyprowadzone na zewnątrz układu scalonego.

Tryb próbkowania

W trakcie normalnej pracy układu dane są przechwytywane w wybranych taktach zegarowych I przesyłane szeregowo ścieżką brzegową.

Zalety i wady techniki brzegowej ścieżki sterująco - obserwującej

• Zalety

• Wielkość i szybkość nadmiaru układowego są mniejsze niż w technice ścieżki sterująco-obserwującej

• Technika ścieżki brzegowej może być użyta do testowania funkcjonalnego i/lub debagowania (uruchamiania programów)

• Testowania funkcjonalnego układu scalonego

• Testowania funkcjonalnego klastrów (makrobloków) układu scalonego

• Emulacji klastru/układu scalonego

• Sterowania wewnętrznych magistral i sieci

• Testowania scalania sprzętu/oprogramowania

• Użycie wewnętrznego skanowania do ładowania/sprawdzania rejestrów, pracy krokowej, ładowania mikrokodu, itd.

• Wada

• Technika brzegowej ścieżki wymaga pewnej dodatkowej powierzchni, prędkości i nadmiaru układowego tego samego rodzaju jak technika ścieżki sterująco-obserwującej

Wykład 5.

Samo-testowanie układów cyfrowych - ang. Built-In Self-Test (BIST)

Samo-testowanie oznacza przeniesienie części lub całości testera do wnętrza układu. Do wnętrza przeniesione zostają najczęściej generator oraz układ odbierający odpowiedzi testowanego układu.

Główne problemy samo-testowania:

1. Minimalizacja układów testera wewnętrznego: nadmiar logiczny i nadmiar powierzchni krzemu

2. Minimalizacja nakładu projektowego na wbudowanie testera

3. Ograniczenie czasu testowania

Generatory wbudowane

Uwzględniając zbiór generowanych pobudzeń testowych rozpatruje się następujące typy testowania:

1. testowanie deterministyczne

2. testowanie wyczerpujące zbiór pobudzeń 2ⁿ

3. testowanie pseudo-wyczerpujące

4. testowanie losowe (pseudoprzypadkowe)

testowanie deterministyczne

Generator testów podaje na wejście testowanego układu wyznaczony uprzednio ciąg pobudzeń testowych pokrywający założony zbiór uszkodzeń testowanego układu. W tym przypadku najczęściej testy zaszyte są w pamięci stałej np.ROM, PROM, EPROM. Ciąg testowy może być zadawany również przez specjalnie do tego zaprojektowany układ układ sekwencyjny, np. układ PLA.

testowanie wyczerpujące i pseudowyczerpujące

Generator testów podaje na wejście testowanego n-wejściowego układu 2ⁿ różnych pobudzeń testowych (wszystkie możliwe kombinacje). Takie testowanie nazywamy wyczerpującym (..wszystkie możliwe stany wektora wejściowego). Sekwencją wyczerpującą może być sekwencja zadawana z układu licznika (licznik binarny, rejestr szeregowy, rejestr liniowy).

Gdy układ można podzelić na poukłady, w taki sposób, że każdy podukład może być testowany testem wyczerpującym, to takie testowanie nazywamy pseudowyczerpującym. Istotne jest, że podział na podukłady dopuszcza części wspólne tych podukładów.

testowanie pseudoprzypadkowe

Generator testów jest generatorem (pseudo..) losowym. Sekwencja losowa zadawana jest zwykle z wyjść rejestru ze sprzężeniem zwrotnym liniowym lub nieliniowym. W zależności od generowanej sekwencji (typ i funkcja sprzężenia zwrotnego oraz stan początkowy rejestru) decyduje o liczbie cykli (taktów) niezbędnych dla uzyskania założonego poziomu współczynnika pokrycia pobudzeń testowych (rysunek poniżej)

Konstrukcje generatorów

Rejestr liniowy - rejestr szeregowy ze sprzężeniem liniowym (ang. LFSR linear feedback shift register)

Sprzężenie liniowe w technice cyfrowej liniowy układ - układ zrealizowany w oparciu o funkcje xor (exclusive-or czyli suma z wykluczeniem)

Rejestr nieliniowy - rejestr szeregowy ze sprzężeniem dowolnym (ang. NLFSR non-linear feedback shift register)

Rejestr liniowy w podstawowej swej postaci może być rejestrem szeregowym (przesuwnym):

• z wewnętrznym sprzężeniem zwrotnym ( na rysunku rejestr powyżej),

• z zewnętrznym sprzężeniem zwrotnym ( na rysunku rejestr poniżej).

• ze sprzężeniem mieszanym: Botom-top, Top-botom

• inne

Testowanie autonomiczne

Testowanie, w którym testowany układ staje się sprzężeniem zwrotnym rejestru szeregowego dołączonego do wejść i wyjść układu

Rejestr MIShR

W testowaniu autonomicznym istotnym problemem jest takie zaprojektowanie układu, który zapewni pokrycie uszkodzeń

Pokrycie uszkodzeń

e = Ne / Nc

Ne - liczba uszkodzeń pobudzonych testem

Nc - globalna liczba

Ne jest zwana również w literaturze optymistyczną liczbą wykrytych uszkodzeń

Wykład 6.

Weryfikatory wbudowane

Weryfikator = kompresor + komparator

• przekształca odpowiedzi testowanego układu cyfrowego w postać krótkiego słowa, które następnie porównuje ze słowem wzorcowym.

Na złożoność weryfikatora wpływa użyta metoda kompresji.

Kompresja liniowa znalazła najszersze zastosowanie w wewnętrznych weryfikatorach.

Przyczyny jej popularności:

• niski koszt jej użycia

• stosunkowo małe prawdopodobieństwo maskowania błędów.

Miara skuteczności

teoretyczna skuteczność EF (ang. Effectiveness) kompresji, która zwykle jest definiowana jako prawdopodobieństwo P, że uzyskane na wyjściu testowanego układu cyfrowego i zawierające wylosowane bity dwa różne ciągi wektorów odpowiedzi u oraz u' są rozróżnialne w rejestrze MISR przez ich sygnatury. Oznaczając przez f funkcję kompresji użytą w weryfikatorze oraz przez s sygnaturę ciągu wektorów u (s = f (u)), teoretyczną skuteczność kompresji można wyrazić w następujący sposób:

EF = P ( f (u) <> f (u') ) = 1 - P ( f (u) = f (u') )

Rys. Porównanie podstawowych struktur testowania wbudowanego w układ.

Na wykładzie przeprowadzono obliczanie efektywności obu powyższych rozwiązań.

Rys. Struktura rejestru MIShR z powyżej przedstawionych struktur testowania wbudowanego w układ

Rys. Tradycyjna struktura testowania wbudowanego w układ

Rys. Budowa rejestru sygnatur MISR a) rejestr ze sprzężeniem wewnętrznym, b) rejestr ze sprzężeniem zewnętrznym.

Rys. Budowa komórek rejestru MISR.

Rys. Jednowejściowe rejestry typu MISR

Dobre właściwości diagnostyczne możnba osiągnąć poprzez odpowiedni dobór sprzężeń zwrotnych generatora i kompaktora.

Rys. Struktury umożliwiające zwiększenie skuteczności testowania w tradycyjnej strukturze BIST

Rys. Dwie modyfikacje struktur BIST z wykorzystaniem licznika jako układu zbierającego odpowiedzi (kompresora) z dodatkowym układem kompensującym: a)specjalny układ kombinacyjny; b) z rejestrem liniowym LFSR.

Struktura BILBO (ang. Built-In Logic Block Obserwer)

Metoda ta łączy funkcje ścieżki sterująco obserwującej i samotestowania

Struktura i tryby pracy rejestru BILBO

Wykorzystanie rejestru BILBO w testowaniu dwóch makrobloków

(dwa rejestry pełnią na przemian role generatora testów i komresora odpowiedzi testowych)

Wykład 7.

Metody określania oraz zwiększania skuteczności testowania wewnątrzukładowego

O efektywności testowania decyduje prawdopodobieństwo wykrycia uszkodzenia.

Prawdopodobieństwo wykrycia uszkodzenia zależy od:

• współczynnika pokrycia uszkodzeń przez strumień generowanych pobudzeń testowych

• skuteczności układu gromadzącego odpowiedzi na testy

Zjawisko obniżające efektywność kompaktora - maskowanie wykrytych przez testy uszkodzeń.

Techniki oparte na rejestrach z liniowym sprzężeniem zwrotnym:

• wysoki współczynnik pokrycia uszkodzeń dla generatora

• stosunkowo niskie prawdopodobieństwo maskowania uszkodzeń dla kompaktora.

Odpowiedni dobór sprzężenia rejestru liniowego kompaktora - poprawa skuteczności stosowania rejestrów liniowych.

Techniki testowania autonomicznego STP i CSTP:

• zależność prawdopodobieństwa wykrycia uszkodzeń od funkcji testowanego układu.

• zwiększenie prawdopodobieństwa poprzez:

• dołączenie dodatkowego liniowego bądź nieliniowego sprzężenia zwrotnego lub

• włączenie zewnętrznego generatora zakłócającego np. rejestru LFSR.

Metody oceny skuteczności testowania wewnątrzukładowego

kryteria oceny:

- efektywność generacji testów,

- efektywność kompakcji odpowiedzi,

- szybkość testowania,

• efektywność testowania,

• stopień wspomagania testowania na wyższych poziomach integracji urządzenia.

UWAGA !

W grupie kryteriów nie uwzględniono rozdzielczości diagnostyki gdyż podstawowym celem testowania układów scalonych nie jest lokalizacja lecz wykrycie uszkodzenia.

Ocena skuteczności generacji pobudzeń testowych

Idealny generator testów - brak powtórzeń w generowanym teście.

I. Ocena generowanego testu za pomocą pokrycia stanów :

stosunek liczby pobudzeń testowych do wszystkich możliwych pobudzeń

II. Entropia stanów rejestru generatora miara zróżnicowania stanów rejestru

entropia :

gdzie:

p_i - prawdopodobieństwo wystąpienia i-tego stanu rejestru,

n - liczba możliwych stanów rejestru.

Ocena skuteczności kompakcji odpowiedzi testowych.

Zjawisko maskowania uszkodzeń (ang. aliasing, fault masking) - utrata informacji wskutek kompakcji danych.

Zjawisko maskowania uszkodzeń występuje gdy podczas zadawania ciągu pobudzeń testowych uszkodzenie zostaje pobudzone, lecz w skutek kompakcji odpowiedzi informacja o pobudzeniu zostaje utracona.

Podczas testowania ciąg odpowiedzi układu uszkodzonego jest różny od ciągu poprawnego lecz końcowy stan przerzutników struktury BIST jest identyczny ze stanem układu sprawnego.

Pokrycie uszkodzeń zwane też "optymistycznym pokryciem uszkodzeń" jest prawdopodobieństwem wykrycia uszkodzeń wyznaczane przy założeniu, że ignorowane jest zjawisko maskowania uszkodzeń. Jeżeli w trakcie testowania uszkodzenie jest wykrywane, to uważa się, że jest ono wykrywane na końcu sesji testowania. Pokrycie uszkodzeń jest zawsze większe od prawdopodobieństwa wykrycia uszkodzeń.

Pokrycie uszkodzeń

e = Ne / Nc (1)

Ne - liczba uszkodzeń pobudzonych testem

Nc - globalna liczba uszkodzeń

Prawdopodobieństwo wykrycia uszkodzeń zwane również "rzeczywistym pokryciem uszkodzeń" (ang. true fault coverage) oznacza pokrycie uszkodzeń uzyskiwane z uwzględnieniem zjawiska maskowania.

Pd = Ntfd / Nc (2)

gdzie Pa - prawdopodobieństwo maskowania,

Nc - liczba rozpatrywanych uszkodzeń (globalna liczba uszkodzeń),

Ntfd - liczba rzeczywiście wykrytych uszkodzeń.

Prawdopodobieństwo może mieć charakter względny, gdy odniesiemy się do jedynie pobudzonych uszkodzeń. Wówczas względne prawdopodobieństwo wykrycia wynosi:

Pde = Ntfd / Nofc (3)

gdzie Pa - prawdopodobieństwo maskowania,

Nofc - liczba pobudzonych uszkodzeń,

Ntfd - liczba rzeczywiście wykrytych uszkodzeń.

Prawdopodobieństwo maskowania wyznaczane jest za pomocą następującego równania

Pa = (Nofd - Ntfd) / Nofd (4)

gdzie Pa - prawdopodobieństwo maskowania,

Nofd - liczba optymistycznie wykrytych uszkodzeń,

Ntfd - liczba rzeczywiście wykrytych uszkodzeń.

Sekwencja niemaskująca - sekwencja o wybranym stanie początkowym i minimalnej długości, która zapewnia założony poziom pokrycia uszkodzeń i maskowanie równe zero.

Zmiany warości prawdopodobieństwa wykrycia uszkodzenia i pokrycia uszkodzeń wraz ze zmianą długości sekwencji testującej - symulacja uszkodzeń w wybranym układzie cyfrowym kombinacyjnym lub sekwencyjnym.

Ocena dynamiki zjawiska maskowania uszkodzeń w kompaktorach

• procesy Markowa

• wyznaczenie entropii sygnatur kompaktora dla kolejnych cykli

Entropia sygnatur nie osiąga wysokich wartości w przypadku niepobudzenia uszkodzenia jest więc równocześnie miarą skuteczności generacji testów. Może być ona miarą równomierności rozkładu prawdopodobieństwa otrzymania sygnatur podobnie jak potencjał rozróżniania.

Modyfikacja ścieżki samotestującej i pierścienia samotestującego dla zwiększenia skuteczności testowania

Trzy struktury wbudowanego do wnętrza układu testera:

• układ wyposażony w autonomiczny generator i kompaktor,

• struktura ścieżki samotestującej (STP) lub

• pierścień samotestujący (CSTP).

Skuteczność struktury wyposażonej w autonomiczny generator i kompaktor zależy od

• liniowego lub nieliniowego sprzężenia zwrotnego rejestru oraz

• stanu początkowego generatora.

*

Nie zawsze pierścień lub ścieżka samotestująca osiągają pożądaną skuteczność diagnostyczną, tzn. odpowiedni poziom pokrycia uszkodzeń oraz niskie prawdopodo-bieństwo maskowania błędów.

**

Acykliczność bądź zbyt krótkie cykle grafu przejść STP (CSTP) mogą prowadzić do zbyt niskiego stopnia pokrycia uszkodzeń testami.

***

Podobnie jak w układach z autonomicznie pracującymi generatorami i kompaktorami, w STP i CSTP informacja o pobudzonym uszkodzeniu może "zaginąć".

****

Zjawisko maskowania zależy w znacznym stopniu od cykliczności grafu. Właściwości diagnostyczne tej techniki są zbliżone do właściwości pierścienia samotestującego.

Pytanie:

Jak zwiększyć efektywność generowania testów i minimalizować zjawiska maskowania uszkodzeń.

Modyfikacja struktury ścieżki i pierścienia samotestującego układem zakłócającym.

Zjawisko znikomego wpływu wielomianu charakterystycznego na wzrost skuteczności diagnostycznej rejestru LFSR:

Rejestr z liniowym sprzężeniem zwrotnym posiada cykliczny graf przejść. Po włączeniu go do pierścienia samotestującego strumień binarny wpływający do niego i zaburzając jego pracę zapobiega pozostawaniu w krótkim cyklu. Rodzaj wielomianu nie wpływa na samo występowanie zjawiska zaburzania lecz tylko jego rozmiar.

Znikomy wpływ rodzaju wielomianu dodatkowo utrudnia dobór wprowadzanego rejestru LFSR

Rys. 2.2. Struktury testowania autonomicznego z układem zakłócającym:

a),c),e) ścieżka samotestująca, b),d),f) pierścień samotestujący;

c),d) układ zakłócający wewnętrzny, e), f) układ zakłócający zewnętrzny

Modyfikacja liniowa struktury ścieżki i pierścienia samotestującego.

Poprawę właściwości diagnostycznych ścieżki i pierścienia można uzyskać również poprzez :

• wprowadzenie dodatkowego układu w pętli sprzężenia zwrotnego zapewniającego m.in. cykliczny graf przejść, a przez to dogodne warunki generacji testu.

• zmianę długości ścieżki (wydłużenie lub skrócenie), a także

• rekonfigurację połączeń rejestru szeregowego z testowanym układem,

Struktura rejestru hybrydowego

Rys. 2.3. Struktura makrobloku wyposażonego w ścieżkę samotestującą z rejestrem hybrydowym; rh- rejestr hybrydowy.

Ocena własności diagnostycznych - badania symulacyjne oparte o modelowanie uszkodzeń w wybranych układach kombinacyjnych ISCAS.

Dla układów tych dokonano doboru ścieżki i pierścienia samotestującego wraz z wbudowanym rejestrem hybrydowym.

Wykres prawdopodobieństwa wykrycia uszkodzeń dla różnych układów modyfikacji liniowej

Wykres prawdopodobieństwa wykrycia uszkodzenia dla układu c499 testowanego techniką pierścienia samotestującego z wbudowanym rejestrem hybrydowym.

p - prawdopodobieństwo wystąpienia uszkodzenia, l - długość testu.

Wykres entropii sygnatur dla kolejnych pobudzeń testowych - układ c499 testowany techniką pierścienia samotestującego z wbudowanym rejestrem hybrydowym.

- entropia stanów, l - długość testu.

Metody zwiekszania efektywności ścieżki i pierścienia samotestującego przez modyfikację nieliniową

Dodatkowy układ sprzężenia zwrotnego umożliwiający generacje zadanego zbioru testow.

Wprowadzenie do ścieżki samotestującej strumieni korygujących

Modyfikacja długości ścieżki i pierścienia: wydłużenie lub skrócenie.

Modyfikacja długości rejestru ścieżki lub pierścienia samotestującegopolega na:

- wprowadzeniu dodatkowych komórek pamięci, lub

- usunięcie komórek odpowiadających liniom wyjść pierwotnych.

Rys. Struktura skondensowanego pierścienia samotestującego

Wykład 8.

TOLEROWANIE USZKODZEŃ

Technika tolerowania uszkodzeń:

• usuwanie błędów

• traktowanie uszkodzeń

Usuwanie błędów - wyeliminowanie błędów ze stanu przetwarzania, jeśli to możliwe, przed wystąpieniem defektu.

Celem traktowania uszkodzeń jest zapobieganie ich ponownego uaktywnienia się.

Usuwanie błędów można przeprowadzić dwoma sposobami:

• poprawianie błędu :

• poprawianie wsteczne i

• poprawianie wyprzedzające oraz

• kompensacja błędu

Poprawianie błędu wymaga identyfikacji błędu przed jego dalszą propagacją do pojawienia się defektu.

Zintegrowanie możliwości funkcjonalnych elementu z mechanizmem wykrywania błędów prowadzi do powstania elementu samosprawdzalnego: sprzętowego lub programowego - konieczność zdefiniowania obszarów dotkniętych błędami

Układy samosprawdzalne

Przykład układu samo-sprawdzającego się

Układ uzupełniony układem kodującym

C - wektor uzupełniający zawierający informację o poprawnym wektorze Y

Możliwe sytuacje:

1. Uszkodzony (tylko) układ podstawowy

Na podstawie stanu wektora C można dokonać wykrycia i korekty wektora Y lub tylko wykrycia błędu

2. Uszkodzony (tylko) układ kodujący

Na podstawie stanu wektora Y można dokonać wykrycia błędu wektora C

3. Uszkodzone obydwa układy

Na podstawie stanu wektora C nie można dokonać wykrycia i korekty wektora Y, co najwyżej tylko wykrycia błędu wektora Y

Układy tolerowania błędów pamięci

a)

Poprawianie błędu - poprawianie wsteczne

b)

Poprawianie błędu - poprawianie wyprzedzające

Techniki poprawiania błędów: a) poprawianie wsteczne; b) poprawianie wyprzedzające.

poprawianie wyprzedzającego - konieczne jest oszacowanie szkód spowodowanych przez wykryty błąd lub przez błędy, które rozprzestrzeniły się przed wykryciem .

Kompensację można stosować systematyczne nawet przy braku błędów, w formie maskowania uszkodzeń (np. głosowanie większościowe).

Ilustracja techniki kompensacji błędu.

Jeśli w kompensacji błędów stosowane jest przełączanie uszkodzonego elementu na inny sprawny element tej samej klasy, to takie podejście do tolerowania uszkodzeń nazywamy wykrywaniem i kompensacją błędu.

Układ głosujący

Liczba układów - n powinna być większa od 2;

Najczęściej n = 3

Układy 1, 2, 3 ... są identyczne; mogą być pełnym układem lub fragmentem układu

Gdy n = 2 wówczas brak możliwości podjęcia decyzji co do poprawności odpowiedzi

Strata efektywnego czasu pracy na usuwanie błędów

• poprawiania błędu, strata czasu jest większa po niż przed wystąpieniem błędu

• poprawianie wsteczne wiąże się z koniecznością zapewnienia punktów nawrotu, czyli w istocie uprzedniego przygotowania do obsługi błędu

• kompensacja błędu, wymagana strata czasu jest praktycznie taka sama, niezależnie od obecności lub braku błędu. Należy zauważyć, że czas trwania kompensacji błędu jest znacznie krótszy niż czas trwania poprawiania błędu, wskutek większej ilości redundancji strukturalnej.

Traktowanie uszkodzeń

I Etap - diagnoza uszkodzenia; polega na określeniu przyczyny błędu; miejsce i typ.

II Etap - osiągnięcie zasadniczego celu traktowania uszkodzeń, tzn. zapobiegnięcie ponownemu uaktywnieniu się uszkodzeń: neutralizacja uszkodzenia - uczynienie uszkodzenia biernym, poprzez usunięcie z dalszej pracy elementu zidentyfikowanego jako uszkodzony.

Techniki tolerowania uszkodzeń obejmują zarówno uszkodzenia przypadkowe jak i celowe.

Zabezpieczenie przed wtargnięciem jest przedmiotem techniki zwanej kryptografią

Istnieją techniki oferujące mechanizmy wykrywania błędów nastawione zarówno na uszkodzenia umyślne jak i przypadkowe. Dotyczy to na przykład technik zabezpieczenia dostępu do pamięci.

Inne techniki zaproponowano dla tolerowania zarówno wtargnięć, jak i uszkodzeń fizycznych, jak również dla tolerowania logiki destrukcyjnej.

Wykład 9.

Klasyfikacja decyzji - reguły wyboru odpowiedzi układów z zastosowaniem kodowania

Klasyfikacja decyzji

1. decyzja jest jedną z informacji: zbiór decyzji pokrywa się ze zbiorem informacji: decyzja punktowa - reguła punktowa

2. „informacji nadanej odtworzyć się nie da” - „dyskwalifikacja” : reguła dopuszczająca dyskwalifikację lub reguła dyskwalifikująca;

3. decyzje obszarowe - podzbiory zbioru informacji; niekoniecznie precyzowana jest przypuszczalna informacja; - reguła obszarowa;

Ilustracja reguł decyzyjnych: a) punktowa; b) dopuszczająca dyskwalifikację; c) obszarowa.

Kody liniowe

1. Ogólny opis kodów liniowych - przykłady,

2. kody cykliczne,

3. kody rekurencyjne

Kody liniowe

Poszukiwanie kodu umożliwiającego stosowanie prostych algorytmów obliczania elementarnych sygnałów tzn. zapewniającego proste kodery i dekodery. Takimi są kody liniowe.

Opis kodów liniowych:

• macierz testów parzystości

• macierz generująca

• macierz form liniowych

Macierz testów parzystości

Opis kodu liniowego systematycznego:

Właściwości kodu systematycznego

1. Jednakowa długość - N ; Pozycje ciągu kodu : informacyjne i kontrolne

Kod nazywamy kodem liniowym systematycznym, jeżeli spełnia on dodatkowo

2. N_K - zespołów kontrolnych: obejmują pozycje informacyjne i kontrolne. Suma cyfr binarnych w pozycjach kontrolnych i należących do zespołu kontrolnego jest parzysta. Na ogół zakłada się, że zespół kontrolny zawiera tylko jedną pozycję kontrolną;

3. Wszystkie ciągi o długości N różniące się w pozycjach informacyjnych, uzyskujące własność 2 są stosowane jako ciągi kodowe

1. s_ln przyjmuje wartości 1 lub 0;

2. dla n < Nk+1 s_ln = x_ln (x_ln - bity ciągu informacyjnego)

3.
(suma modulo 2)

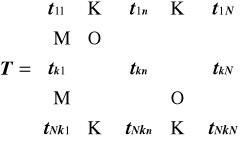
Przykład kod Hamminga o długości N = 7 korygujący 1 błąd, w którym

• do zespołu kontrolnego k = 1 należą pozycje: 1, 3, 5, 7

• do zespołu kontrolnego k = 2 należą pozycje: 2, 3, 6, 7

• do zespołu kontrolnego k = 3 należą pozycje: 4, 5, 6, 7

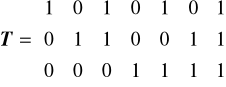
W przypadku grupowania bitów kontrolnych i pozycji informacyjnych

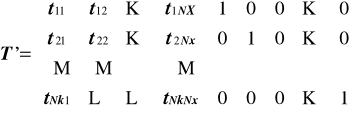
(1)

Ciąg kodowy kodu liniowego przyporządkowany sumie dwu informacji jest równy sumie ciągów kodowych przyporządkowanych poszczególnym informacjom

(2)

Suma dwu ciągów kodowych kodu liniowego jest znów pewnym ciągiem kodowym

Macierz generująca kod

g_{m =} s[x^(m)]

x^(m) , m = 1, 2, ...,Nx - ciąg informacji elementarnych składających się z jedynki w m-tej pozycji oraz zer w pozostałych pozycjach

x_l = x_l1 ,..., x_lNx ,

Kod Hamminga

Kody liniowe o długości N = 2^μ - 1 gdzie μ jest liczbą naturalną

Kolumny stanowią wszystkie kombinacje μ zer i jedynek oprócz kombinacji samych zer

Macierz testów ma μ wierszy, a zatem

N_K = μ

N_X = 2^μ - μ - 1

Wydłużony kod Hamminga

- dodatkowy test obejmujący wszystkie pozycje

N = 2^μ

N_K = μ + 1

N_X = 2^μ - μ - 1

Inne kody liniowe:

Kody Reeda-Mullera

Kody z ciągami o jednakowej odległości

Kody łączone i iterowane

Kody Reeda-Mullera

N = 2^μ

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
A(0)	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
A(1)		1		1		1		1		1		1		1		1
A(2)			1	1			1	1			1	1			1	1
A(3)					1	1	1	1					1	1	1	1
A(4)									1	1	1	1	1	1	1	1

Kod Reeda-Mullera rzędu ν (ν liczbą naturalną)

ν < μ

gdy wierszami macierzy generującej są ciągi:

a(0), a(j) (j=1,2,3,.., μ) oraz

wszystkie różne iloczyny ciągów a(j) obejmujące ν lub mniej ciągów a(j)

Przykład:

μ = 4 oraz ν = 2

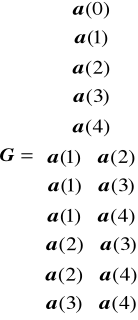
Przykład układu realizującego kodowanie i dekodowanie słów ciągów liniowych

Wykład 10.

KODY CYKLICZNE

Kody ilorazowe

W(,h) = h₀ + h₁*¹ + h₂*² * + ... + h_n-2*^n-2 * + h_n-1*^n-1 + h_n*ⁿ

Suma (+) oznacza sumę modulo 2

Działania na wielomianach

• suma (modulo 2)

• różnica odpowiada operacji sumy

• iloczyn

• iloraz

Rozważamy wielomiany o postaci:

A() = a₀ + a₁*¹ + a₂*² * + ... + a_n-2*^n-2 * + a_n-1*^n-1 + a_n*ⁿ

Rozpatrzmy dwa wielomiany:

A() = a₀ + a₁*¹ + a₂*² * + ... + a_n-2*^n-2 * + a_n-1*^n-1 + a_n*ⁿ

B() = b₀ + b₁*¹ + b₂*² * + ... + b_n-2*^n-2 * + b_n-1*^n-1 + b_n*ⁿ

Suma wielomianów C() = A() + B()

C() = c₀ + c₁*¹ + c₂*² * + ... + c_n-2*^n-2 * + c_n-1*^n-1 + c_n*ⁿ

gdzie:

c_i = a_i ⊕ b_i

Iloczyn wielomianów A() i B()

D() = A() * B() = d₀ + d₁*¹ + d₂*² * + ... + d_n-2*^n-2 * + d_n-1*^n-1 + d_n*ⁿ

gdzie:

d_i = a_ib₀ ⊕ a_i-1b₁ ⊕ _ai-2b₂ ⊕ ... ⊕ a₀b_i

i = 0, 1, ... , n+m

Odwrotnym działaniem do mnożenia wielomianów jest dzielenie wielomianów. A() i B()

Wynikiem dzielenia wielomianów jest iloraz D() w postaci wielomianu stopnia będącego różnicą stopni wielomianów A i B oraz reszta R() w postaci wielomianu stopnia o 1 niższego od wielomianu B. Zależność pomiędzy wielomianami można zapisać w postaci równania:

A() = D() * B() + R()

1. W przypadku iloczynu stopień wynikowego wielomianu jest sumą stopni wielomianów składowych

2. W przypadku ilorazu stopień wynikowego wielomianu jest różnicą stopni wielomianów, a wynik w przypadku niepodzielności obejmuje również resztę

Rys.1. FF - przerzutniki typu D; h_i=1 oznacza połączenie , h_i=0 oznacza brak połączenia.

h_n= 1

Rysunek 1.

Jeżeli na wejście Si podany zostanie ciąg W(,g) , wówczas po m taktach zegarowych (m - długość ciągu wejściowego) otrzymamy:

• na wyjściu ostatniego przerzutnika FF_n-1 wynik dzielenia wielomianów W(,g) / W(,h)

• w komórkach rejestru resztę z dzielenia wielomianów

Rys. 2.

Rysunek 2.

Równoważny pod względem generowanego wyniku dzielenia wielomianów jest rejestr ze sprzężeniem zewnętrznym dla którego:

p_i = h_n-i

dla każdego i = 0,1,2,...,n

Rejestr opisany wielomianem pierwotnym, pierwszym generuje cyk o długości 2ⁿ - 1

Przykłady dzielenia wielomianów

Przykład 1.

A() = ⁹ +⁷ +⁶ +⁴ + oraz B() = ⁴ +² +1

Po wykonaniu operacji dzielenia otrzymujemy:

iloraz : D() = ⁵ +² + oraz reszta : R() = ³ +²

Binarna reprezentacja wielomianów i dzielenia:

1	0	0	1	1	0			iloraz
1	0	1	1	0	1	0	0	1	0	:	1	0	1	0	1
1	0	1	0	1
=	=	=	1	1	1	0	0
			1	0	1	0	1
			=	1	0	0	1	1
				1	0	1	0	1
				=	=	1	1	0	0		reszta

2. Kody ilorazowe

Oznaczmy przez W(,h) wielomian zbudowany na ciągu (wektorze h), taki , że

W(,h) = h₀ + h₁*¹ + h₂*² * + ... + h_n-2*^n-2 * + h_n-1*^n-1 + h_n*ⁿ

oraz przez G() wielomian:

G() = g₀ + g₁*¹ + g₂*² * + ... + g_G-2*^G-2 * + g_G-1*^G-1 + g_G*^G

Kod nazywamy kodem ilorazowym, jeżeli:

1. ciągi kodowe mają taką samą długość N >= G + 1;

2. określony wzorem wielomian W(,s) związany z dowolny ciągiem kodowym s jest podzielny przez wielomian G(), a więc :

w(, s) = m()*g()

przy czym m() jest pewnym wielomianem stopnia nie większego niż N - G - 1 . Wielomian g() nazywamy wielomianem generującym kod.

Pierwszy kod ilorazowy

K₁

Przyjmijmy założenia:

1. G = N - N_x - N_k ,

2. m() = w(, x) ,

3. s- słowo kodowe oraz

4. w(, s) = w(,x)*g() w(, s) = m()*g()

x^(m) = 0,0,0,0,1,0,0,0,0

-----------------^m----------

w(,x^(m)) = ^m-1

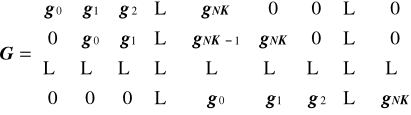
G(x) = x⁴ + x² + 1

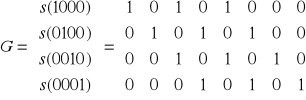
Drugi kod ilorazowy

K₂

Wadą pierwszego kodu ilorazowego jest to, iż jest on kodem niesystematycznym, tzn. ciągi kodowe nie mają wyróżnionych pozycji informacyjnych. Dla wyeliminowania żmudnej procedury przekształcania macierzy generującej kod do postaci kanonicznej wprowadzono drugi kod ilorazowy oznaczony przez K₂.

Załóżmy , że:

^G * w(,x) = m() * g() + r()

Stąd:

w[ , s(x)] = - r() + ^G * w(,x)

Wówczas:

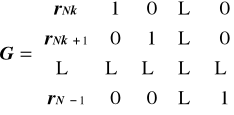
Wynika to stąd, że wielomian r() jest stopnia =< G-1 , najniższa zaś potęga wielomianu jest równa co najmniej G. Zatem w ciągu kodowym s(x) pozycje - począwszy od G-tej są pozycjami informacyjnymi, zaś pozycje 0,1,...,G-1 - kontrolnymi.

Przykład:

g() = ⁴ + ² + 1

Wektor g = {g₀ g₁ g₂ g₃ g₄} = { 1 0 1 0 1 }

Macierz generująca pierwszy kod ilorazowy G dla czterobitowego słowa informacyjnego x:

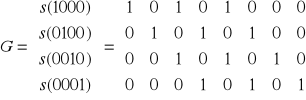
Macierz generująca drugi kod ilorazowy G dla czterobitowego słowa informacyjnego x wymaga przeprowadzenia operacji dzielenia w celu uzyskania reszt.

Wielomiany ⁴ * W(,x^(m)) = ^m (G = 4) dzielone będą przez wielomian g() = ⁴ + ² + 1

W(,x⁽¹⁾) = ⁰ , W(,x⁽²⁾) = ¹ , W(,x⁽³⁾) = ² , W(,x⁽⁴⁾) = ³

1	0	1	0					Iloraz
1	0	0	0	0	0	0	0	:	1	0	1	0	1
1	0	1	0	1
=	0	1	0	1	0			reszta r^0
	0	0	0	0	0
	=	1	0	1	0	0		reszta r^1
		1	0	1	0	1
		=	0	0	0	1	0	reszta r^2
			0	0	0	0	0
			=	0	0	1	0	reszta r^3

Otrzymujemy macierz generującą kod:

Definicja kodu cyklicznego

Kod ilorazowy o długości N nazywamy kodem cyklicznym, jeżeli wielomian generujący g() jest dzielnikiem wielomianu ^N+1, tzn., jeżeli istnieje taki wielomian h(), że

g()*h() = 1 + ^N (1)

Z założenia, że w wielomianie g() współczynnik przy potędze ^G jest równy 1, wynika,że:

wielomian h() jest stopnia N_x

Jeśli jest dany wielomian generujący g(), to należy znaleźć takie N, aby był spełniony warunek (1). W związku z tym wprowadzimy pojęcie Rzędu wielomianu.

Rzędem wielomianu g() nazywamy najmniejszą liczbę całkowitą NG taką, że wielomian 1 + ^NG jest podzielny przez g()

Przy znajdowaniu rzędu wielomianu jest pomocne następujące twierdzenie:

Wielomian 1 + ^2n-1 jest podzielny przez:

1. każdy wielomian pierwotny stopnia n,

2. każdy wielomian pierwszy stopnia n,

3. każdy wielomian pierwszy stopnia będącego dzielnikiem liczby n, w tej liczbie i przez wielomian 1 + 

Wielomianem pierwszym stopnia n nazywamy wielomian, który nie jest podzielny przez żaden wielomian stopnia niższego (z wyjątkiem wielomianu stopnia 0, jakim jest 1). Wielomian pierwotny stopnia n jest to taki wielomian pierwszy, którego rząd jest równy 2ⁿ-1.

3. Konstrukcja układu EDAC

EDAC - układ wykrywający i korygujący błędy

Parity Generator (PG)- układ generujący część kontrolną kodu - oznaczmy ją przez c. Układ PG realizuje zależności opisane macierzą generującą kod.

Część kontrolna kodu wyznaczona na podstawie części informacyjnej jest porównywana z częścią kontrolną uzyskiwaną na wejściu układu EDAC.. Wektor s oznacza różnicę (mod 2) tych części kontrolnych. Jeżeli s = 0, to oznacza, że słowo kodowe podawane na wejście układu EDAC jest poprawne. Załóżmy błąd na pojedynczym wejściu informacyjnym. Można udowodnić, że s przyjmuje wartość części kodowej słowa zbudowanego na informacji elementarnej s(x^(m)), przy czym m oznacza numer linii, na której pojawił się błąd.

Dekoder błędu (Error Decoder) dekoduje stan wektora s. Pojawienie się jednego ze stanów s(x^(m)) powinno zmienić stan m-tej linii na przeciwny, co oznacza, że na m tym wyjściu dekodera powinna pojawić się jedynka. Dekoder będzie zawierał bramki AND, każda połączona z wszystkimi liniami s, z negacjami na tych wejściach, na których słowo s posiada zera.

Przykład

30

---