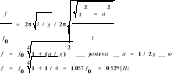
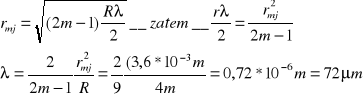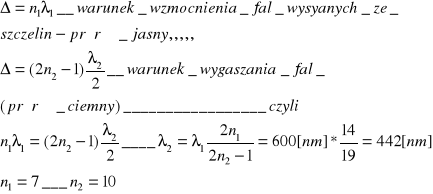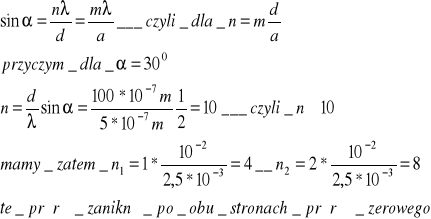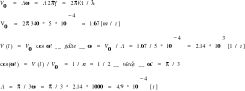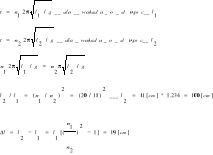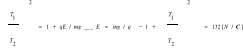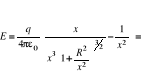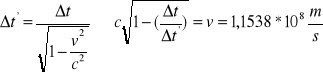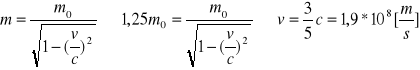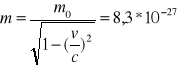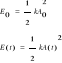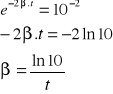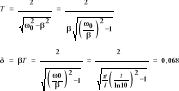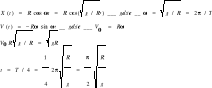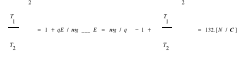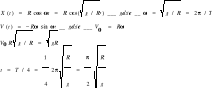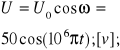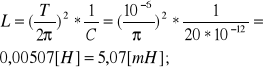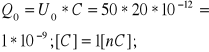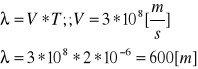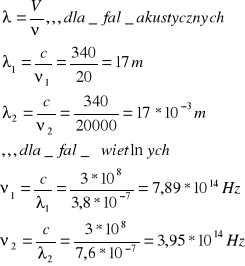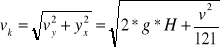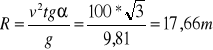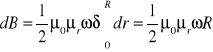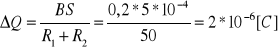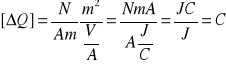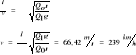ZASADA ZACHOWANIA MOMENTU PĘDU D.109 Stolik poziomy obraca się z prędkością kątową ω. Na środku stolika stoi człowiek i trzyma w wyciągniętych rękach w odległości l od osi obrotu dwa ciężarki o masie m każdy. Jak zmieni się prędkość obrotów stolika gdy człowiek opuści ręce? Ile razy wzrośnie energia kinetyczna układu? Moment bezwładności stolika wraz z człowiekiem (bez ciężarków) wynosi I.
Z zasady zachowania krętu mamy (I+2ml2)ω=Iω1
D.110 Na poziomo wirującym pręcie o masie M, przez środek którego przechodzi prostopadle do ziemi oś, siedzi małpka o masie m. Pręt ma długość l i wiruje z prędkością kątową ω1.Jaka będzie prędkość kątowa po przejściu małpki do środka?
Iω=const Zasada zachowania krętu
POLA SIŁ D64
W stałym polu elektrycznym o natężeniu E=15V/m elektron przebywa w kierunku pola drogę s=2m z prędkością średnią v=2000 km/s. Oblicz przyrost prędkości elektronu. Stosunek ładunku elektronu do jego masy
Ruch jest jednostajny przyśpieszony
F=eE=ma
S=vt
Ale vk=v0+at
……… D65 Strumień elektronów rozpędzony polem elektrycznym o napięciu U1 = 5000 V wpada między okładki kondensatora płaskiego równolegle do jego okładek. Jakie napięcie należy przyłożyć do okładek kondensatora, by strumień elektronów został odchylony o h=3 mm. Długość kondensatora jest l=5 cm, odległość między okładkami d=1.5 cm.
ale eE=ma
gdzie
mamy zatem
D66 Naładowany pyłek o masie m = 2.4 * 10-8g znajduje się w równowadze w polu elektrostatycznym kondensatora płaskiego. Znaleźć liczbę elektronów znajdujących się na pyłku, jeżeli różnica potencjałów przyłożona do płytek kondensatora U=3000 V, a odległość między płytkami d=2 cm. Ładunek elektronu e = 1.6*10-19 C.
Fel=eE=mg - warunek równowagi pyłku
Gdzie
D67 W oleju o gęstości ρ1 = 800 kg/m3 wytworzono pionowe, jednorodne pole elektryczne o natężeniu E = 3.6 * 106 V/m. W polu tym umieszczono naelektryzowaną kulkę o promieniu r=5 mm i gęstości ρ2 = 8600 kg/m3. Obliczyć ładunek kulki, jeżeli wiadomo, że pozostaje ona w spoczynku.
Warunek równowagi kulki
gdzie
FALE II D43. Znaleźć długośćc fali de'Brogile'a neutronu, którego energia jest równa średniej energii termicznej w temp. T=300K Dana jest masa neutronu m=1,675*10^-27 kg
D44.Promień krzywizny soczewki płasko wypukłej wynosi 4m. Ile wynosi długość fali λ padającego światła jeśli promień 5-tego jasnego pierścienia Newtona w świetle odbitym wynosi 3,6mm
D45.W doświadczeniu Younga wzięto najpierw światło o długości fali λ1=600nm a potem o długości fali λ2. Jaka jest długość fali jeśli 7-prążęk jasny w pierwszym przypadku pokrywa się z 10 ciemnym w przypadku drugim.
D46.Stała siatki dyfrakcyjnej d=10^-2mm, a szerokość części przeźroczystej a=2,5*10^-3mm.Ile maksimów interferencyjnych z jednej strony z jednej strony maksimum zerowego do kąta α=30stopni będzie nieobserwowanych wskutek pokrycia się z głównymi minimami dyfrakcyjnymi dla długości fal λ=5000A? Warunek otrzymania pod kątem α minimum interferencyjnego przy dyfrakcji Fraunhoffera na szczelinie o szerokości a wynosi asinα=nλ (m=1,2,3,4,...). Natomiast siatka dyrakcyjna daje maksima interferencyjne pod kątem α, gdy
D38. Równanie źródła drgań jest u=4sin(600πt)cm. Znaleźć dla rozchodzącej się fali płaskiej wychylenie z położenia równowagi w punkcie odległym o l=75cm od źródła, po upływie τ=0.01s od rozpoczęcia drgań. Drgania rozchodzą się z prędkością v=300m/s.
D39. Równanie źródła drgań jest u=Asin((2πt)/T). Wychylenie z położenia równowagi punktu, znajdującego się w odległości 4 cm od źródła drgań, w chwili t=T/6 jest równe połowie amplitudy. Znaleźć długość fali płaskiej powodującej to wychylenie.
DRGANIA HARMONICZNE
D79.Maksymalna prędkość punktu drgającego ruchem harmonicznym Rozw
Równanie ruchu drgającego ma postać
Przy czym u nas
Prędkość
Przysp
Czyli D80 Drgający harmonicznie kamerton jest źródłem fali akustycznej o długości λ i prędkości v. Obliczyć maksymalną prędkość punktu kamertonu drgającego z amplitudą A. Po jakim czasie prędkość tego punktu będzie n razy mniejsza od prędkości maksymalnej? Obliczenia numeryczne wykonać dla λ=1m, v=340m/s,A=0.5mm, n=2. Rozw wiadomo, że λ=VT=V/γ wtedy γ=V/ λ
Ponieważ D81 Jak należy zmienić długość l wahadła matematycznego, aby skompensować wpływ przyrostu temperatury ΔT na jego okres wahań? Współczynnik cieplnej rozszerzalności liniowej nici wahadła wynosi λ. Obliczenia numeryczne wykonać dla l=100cm,ΔT=50K, λ=2/100000[1/K]. ROZw okres drgań wahadła matematycznego wynosi
D82 Wahadło matematyczne o długości
Rozw D83 Jeżeli wagon jest w spoczynku to częstotliwość drgań wahadła matematycznego znajdującego się w tym wagonie wynosi f=0.5Hz. Oblicz częstotliwość drgań tego wahadła w wagonie poruszającym się po torze poziomym z przyspieszeniem a=4.9m/(s*s). Płaszczyzna drgań wahadła jest równoległa do kierunku ruchu wagonu. Przyspieszenie ziemskie g=9.8m/(s*s).
Rozw Łatwo wykazać, że okres drgań wahadła mat o długości l wyraża się wzorem
D84 Okres wahań matematycznego wahadła wykonanego z nieprzewodzącej nici i małej kulki o masie m=25g wynosi
Rozw okres drgań wahadła wynosi
stąd
POLE ELEKTRYCZNE D 20. Dwa nieskończenie długie, równoległe przewodniki, naładowane ładunkiem tego samego znaku z tą samą gęstością liniową λ, leżą w odległości d od siebie. Określić potencjał pola elektrycznego w punkcie leżącym w odległościach, odpowiednio r1 i r2 od tych przewodników. Przyjąć, że potencjał pola od jednego przewodnika jest równy zeru w odległości d od niego.
Walec współśrodkowy stanowi pow. Gaussa, stąd: Ψe=ES⊥=E 2Πrl oraz Ψe=ΣQi/E0 → E=λ/2ΠE0r ponieważ E=-dϕ/dr to dϕ=-Edr= -λ/2ΠE0 *dr/r Δϕ=ϕ(r) - ϕ(d) = -λ/2ΠE0 d∫r dr/r = -λ/2ΠE0 ln(r/d) Z war. zadania ϕ(d) Stąd ϕ(r1)=λ/2ΠE0 ln(d/ r1) ϕ(r2)=λ/2ΠE0 ln(d/ r2) ϕc=ϕ(r1)- ϕ(r2)=λ/2ΠE0 [ln(d/ r1)+ ln(d/ r2)]= λ/2ΠE0 ln(d2/r1r2)
21- Cienki pręt o długości 2a został naładowany ze stałą gęstością liniową ładunku Dzielimy pręt na bardzo małe fragmenty o długości dx, na których jest ładunek dq=λdx. Natężenie pola elektrycznego od tego ładunku wynosi:
gdy a<<r to:
potencjał pola wynosi:
ale ln(1+x)≈x dla x<<1 (rozwinięcie w szereg), zatem: 22- Ładunek elektryczny +q rozłożony jest równomiernie na cienkim drucie tworzącym okrąg o promieniu r. Okrąg ten leży w płaszczyźnie YOZ kartezjańskiego układu współrzędnych tak, że jego środek pokrywa się z początkiem układu. W początku układu współrzędnych znajduje się ładunek -q. Znaleźć zależność natężenia pola elektrycznego od współrzędnej X, w dużej odległości od układu ładunków, czyli dla |x| >> r. Każde dwa symetrycznie położone fragmenty pierścienia tworzą identyczny układ sił pola elektrycznego.
23- Wzdłuż cienkiego pierścienia o promieniu R rozłożony jest równomiernie ładunek +q. Znaleźć prędkość ładunku -q o masie m w chwili przechodzenia przez środek pierścienia, jeśli ładunek -q początkowo spoczywa w punkcie A na osi pierścienia w bardzo dużej odległości od niego. Analogicznie jak w zadaniu 22 układ równoważny jest takiemu:
24- Korzystając z prawa Gaussa znaleźć natężenie pola elektrycznego wytwarzanego przez nieskończoną płaszczyznę z gęstością powierzchniową σ.
|
D68 Ciało o masie m = 10-3 kg i ładunku Q = 10-4 C porusza się w jednorodnym polu elektrostatycznym o natężeniu E = 100 j V/m. Prędkość początkowa wynosi v =v0 i m/s. W dowolnie wybranym układzie współrzędnych obliczyć tor cząstki r (t) i jej prędkość v (t).
ale
49.Elektron o energ. Kinetycznej E wlatuje w jednorodne pole magnetyczne B. Ładunek elektr. wynosi e, masa m. Wektor prędkości elektronu leży w płaszczyźnie prostopadłej do linii pola sił. Obliczyć: promień, częstotliwość.
F=evB=F=, , v= , , f== =
50.Naładowana cząstka porusza się w polu magnetycznym po okręgu o promieniu R z prędkością v . Indukcja pola magnetycznego jest B. Znaleźć ładunek q cząstki, jeśli jej energia kinetyczna jest równa .
= F = qvB , E= ,v= q= = = mv=qBR , m= , qBR= qBR= , q =
51.Dwa jony mające jednakowy ładunek elektryczny, ale różne masy, wpadają do jednorodnego pola magnetycznego prostopadle do kierunku pola. Pierwszy jon porusza się po okręgu o promieniu r, drugi o promieniu r. Określić stosunek mas jonów, jeżeli zostały one przyspieszone jednakową różnicą potencjałów
Ug = = to poniewarz qvB= to , , zatem = = 52.Naładowana cząstka po przejściu przez przyspieszającej różnicy potencjałów U wpada w skrzyżowane pod kątem prostym pola: elektryczne o natężeniu E i magnetyczne o indukcji B. Znajdź stosunek ładunku tej cząstki do jej masy, jeśli cząstka porusza się po torze prostoliniowym w kierunku prostopadłym do obu pól.
Uq = , to v = ruch jest prostoliniowy gdy F= qE = F= qvB czyli v = , = 2U , = SIŁY BEZWŁADNOŚCI Zad 31 Rakieta o masie m0 ,siły zewnętrzne pomijalnie małe, t=0 włączony silnik wyrzuca gazy z prędkością u względem rakiety. Wydajność silnika μ= -(dm)/(dt) (m -aktualna masa rakiety). Znaleźć zależność prędkości od masy i siłę ciągu. F=m(t)*(dv)/(dt)+vwzgl[(dm)/(dt)] (rów. ruchu rakiety); m(t)=m0-μt (m0 - aktualna masa rakiety); (dm)/(dt)=μ; vwzgl=u ; F=0 - z warunków zad.; m(t)*(dv)/(dt)= - u*(dm)/(dv); (m0-μt)*(dv)/(dt)= -μu; dv=- μu(dt)/(m0-μt); 0∫v(t) dv= - μu* m0 ∫ m0-μt (dt)/(m0 -μt); (podstawiamy: m0-μt=z i dt= (-1/μ) *dz); v(t)= u* m0 ∫ m0-μt (dz)/z; [* v(t)=u*ln(m0/(m0-μt)) *]; Fciągu=Fodrzutu=vwzgl (dm)/(dt); [* Fciągu= μu *]; Zad 32 Na transporter sypie się piasek z szybkością μ. Obliczyć moc jeśli transporter ma mieć prędkość v. F=m(t)*(dv)/(dt) + v*(dm)/(dt) (rów. ruchu wózka); μ=(dm)/(dt); (dv)/(dt)=0 (bo v jest const.) więc F=μv; [* P=Fv=μv2 *] Zad 54 Energia potencjalna cząstki w pewnym polu ma postać: U=a/r2 - b/r , gdzie a i b są const. >0, a r jest odległością od centrum pola. Wyznaczyć wartość r0 odpowiadającym położeniu równowagi. Czy trwale? (dU)/(dr)=0 (warunek ekstremum-położenie równowagi); b/r0 2 - 2a/r0 3=0; [* r0=2a/b *]; (d2U)/(dr2)>0 (warunek aby równowaga była trwała przy założeniu r=r0); (6a/r0 4 - 2b/r0 3) >0; [*b4/8a3 >0*] warunek spełniony; Zad.55 Energia potencjalna w atomie wodoru U= -( e2)/(4∏ε0r) gdzie e - ładunek elektronu, ε0 przenikalność dielektryczna próżni, r odległość elektr . od jądra. Zał. elektron porusza się po orbicie kołowej. Z postulatu Bohra: moment pędu: L=mvr=(nh)/(2∏) (1*), gdzie: m - masa elekt., v prędkość na orbicie, n - liczba naturalna, h stała Plancka obliczyć : a) energie całkowitą E , b)promienie orbit, c) prędkość i przyspieszenie na 1 orbicie. Fel=Fod; Fel=e2/(4∏ε0r2); Fob=(mv2)/r; II postulat Bohra: Ec=(mv2)/2+U; mrv2=e2/(4∏ε0) (2*); (2*) : (1*) => v=1/n * e2/(2∏ε0)=1/n*v1 z (1*) r=(nh)/(2∏mv); [* r=n2*(ε0h2)/(∏me2)=n2*r1 ]; podstawiając do II postulatu Bohra otrzymamy: [* E=-(me4)/(8ε02h2n2) *]; [* v1=e2/(2∏ε0) ] ; a=v2/r=(∏me6)/(4ε03h4n4); n=1 (1 orbita) ; [* a1=(∏me6)/(4ε03h4) *]. Zad 56 Sztuczny satelita krąży dookoła Ziemi (promień R) po orbicie o promieniu r. Obliczyć okres obiegu. Fgr=G*(Mm)/r2; Fodś=(mv2)/r; MG=gR2; T=(2Πr)/v; Fgr=Fodś; v2=M*G/r=(gR2)/r; T=(2Πr)/√((gR2)/r); [* T=(2Πr)/R *√(r/g) *]; Zad 57 Na jakiej wysokości h ciężar jest n razy mniejszy od ciężaru na powierzchni Ziemi (promień R)? Fr=(GMm)/r2=mgr ; FR=(GMm)/R2=mgR; gr / gR = 1/n; r2=nR2; h=r-R; [* h=R(√n -1) *]; (r - odległość miejsca od środka Ziemi);
SZCZEGÓLNA TEORIA WZGLĘDNOŚCI 94 - W tym samym miejscu korony słonecznej w odstępie 12s nastąpiły dwa wybuchy. Rakieta poruszająca się ze stałą prędkością względem Słońca zarejestrowała oba zdarzenia w odstępie 13s. a) ile wynosi odległość czasoprzestrzenna Δl między wybuchami w układzie związanym z poruszającą się rakietą ? b) Jaką prędkość i jaki kierunek ma wektor prędkości rakiety?
Dylatacja czasu: 95 - Czy można znaleźć taki układ odniesienia, w którym Chrzest Polski i bitwa pod Grunwaldem zaszłyby: a) w tym samym miejscu? b) w tym samym czasie?
Δs2>0 czyli interwał czasoprzestrzenny jest typu czasowego, a wiec można znaleźć układ, w którym oba zdarzenia zajdą w tym samym miejscu, natomiast nie można znaleźć układu, w którym oba zdarzenia zaszłyby w tym samym czasie. 97 - Długość nieruchomego pociągu jest taka sama jak długość tunelu. Pociąg ten jedzie z prędkością v. Czy początek i koniec tego pociągu miną końce tunelu dokładnie w tej samym momencie czasu ?
NIE MAM ROZWIĄZANIA, TWOJE JEST ZŁE!!! D 98. Znajdź energię wydzielającą się przy powstawaniu z protonów i neutronów 1g helu, korzystając z następujących danych mp=1,001509 jma, masa neutronu mn=1,008665 jma, masa jądra helu mHe=4,001509 jma, 1 jma =1,6604 10-27 , liczba Avogadro Na=6,025 1023 1/mol,. Prędkość światła w próżni c=3 108 m/s.
Obliczamy defekt masy z równania Δm = 2 mp + 2 mn - mHe Energia wydzielana przy powstawaniu jednego jądra helu wynosi: E=Δmc2 =(2 mp + 2 mn - mHe ) c2 Obliczamy liczbę jąder N w jednym gramie helu: N= Na m/μ gdzie m=1g, μ-liczba atomowa (μ=2) E=[2(mp + mn)- mHe ] c2 Na m/μ ENERGIA RELATYWISTYCZNA 99 - Znajdź energię wydzielającą się przy powstawaniu z protonów i neutronów 1 g helu. Dane: masa protonu mp=1.001509 jma, masa neutronu mn=1.008665 jma, masa jądra helu mHe=4.001509 jma, 1 jma=1.6604*10-27kg, liczba Avogardo NA=6.025*10-23 mol-1, c=3*108 m/s.
E=2Ep+2En+2Ee-EH 2Ee jest tak małe, że można je pominąć E=2c2(mp+mn)-c2mHe=c2(2*2.016942-4,001509)=c2*0,32374 jma=3*108 eV 1 jma = 1.6604*10-27kg=9.3 * 108 eV N=(m/μ)*NA=1/4*6.025*1023=1.51*1023 EC=N*E=7,25*1019 kJ N - liczba atomów w masie m, μ - masa molowa 100 - Kreację pary cząsteczek elektron-pozyton uzyskano za pomocą promieniowania elektromagnetycznego o częstotliwości f=6*1020Hz. Oblicz energię kinetyczną uzyskanych cząstek. Masa spoczynkowa elektronu m0=9*10-31 kg, stała Plancka h=6.6*10-34 Js, c=3*108 m/s.
E=hf=2,4750 MeV 2EK=hf-2m0c2 EK=[(hf)/2]-m0c2=(E/2)-E0 E0=0.50625 MeV EK=0,72525 MeV (1eV=1.6*10-19J)
101 - Relatywistyczna masa poruszającej się cząstki jest n=1.25 razy większa od jej masy spoczynkowej. Oblicz prędkość cząstki. c=3*108m/s. 102 - Cząstka o masie spoczynkowej m0 przyspieszona została do prędkości v=0.6c. c=3*108m/s. Jak zmieniła się masa cząsteczki i jaka jest jej energia kinetyczna ? (m0 =6.64*10-27kg)
m=1.25m0 EK=(m-m0)c2=0.25m0c2=1,5*10-10 [J]
103 - W wyniku rozpadu pewnej cząstki powstają dwie nowe cząstki o masach m1 i m2. Wartości pędów powstałych cząstek wynoszą odpowiednio p1 i p2, a kąt między nimi równy jest α. Jaka była masa M rozpędzonej cząstki ?
p=p1cosα1+p2cosα2 p1sinα1=p2sinα2 α1+α2=α (rozwiązać należy ten układ równań)
POLE ELEKTRYCZNE
D26. W jednorodnie naładowanej kuli, z gęstością objętościową
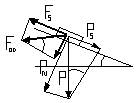
D27. Do dwóch uziemionych kulek metalowych B i C, o promieniu R, znajdujących się w odległości r>>R, zbliżono kulkę A o tym samym promieniu, naładowaną ładunkiem QA również na odległość r tak jak na rysunku obok. Znaleźć jakim ładunkiem QB i QC naładują się kulki B i C oraz jaką pracę wykonała siła zewnętrzna, jeśli kulka została przeniesiona z nieskończoności. A B C
Na kulkach B i C indukuje się ładunek przeciwnego znaku. Ten ładunek można obliczyć metodą „obrazów zwierciadlanych”. Wtedy otrzymamy QB=-QA*(R/r) analogicznie QC=-QA*(R/2r) Praca sił zewnętrznych przy przesuwaniu ładunku QA z nieskończoności odpowiada energii potencjalnej układu ładunków. Wiadomo, że W=k*(q1*q2)/r , zatem W=k*(QA*QB)/r+k*(QA*QC)/2r+k*(QB*QC)/r zatem W=(1/(4rQAQB+(QAQC)/2+QBQC]= (1/(4r-QA2(R/r) -QA2(R/2r)+ + QA2(R2/2r2)]=(QA2/(4r3))[-Rr-(Rr/2)+R2/2]= (QA2/(8r3))[-3Rr+R2] W=((QA2R)/(8r3))(R-3r) ponieważ r>>R to W-((3QA2R)/(8r2))
D28. Kondensator płaski ma okładki kwadratowe o boku l znajdujące się w odległości d od siebie. Pomiędzy te okładki wstawiono ściśle dopasowany blok dielektryka o względnej przenikalności elektrycznej równej . Po naładowaniu kondensatora do napięcia U źródło napięcia odłączono. Następnie wyciągnięto dielektryk równolegle do okładek, tak że na odcinku o długości x pomiędzy okładkami kondensatora było już tylko powietrze. Na odcinku o długości l-x nadal pozostawał pomiędzy okładkami kondensatora blok dielektryka. Wyznacz wartość i kierunek siły zewnętrznej
l-x po wyciągnięciu płytki o x mamy dwa
(sumują się ładunki na płytkach), czyli
_____ =(1/2)r(l2/D)U2(Co/C1) | D | ___ W=(1/2)r(l2/D)U2[(r(l2/D))/
_ /((lx/D)+r((l-x)l)/D)]= =(1/2)r* *(l2/D)U2*((rl)/(x+r(l-x))) Ponieważ to F=(1/2)r2(l3/D)U2[(1-r)/(x+r(l-x))2]= (1/2)r2(l3/D)U2* *(-(r-1)/(rl-x(r-1))2)= -(r2 l3U2)/[2D(r-1)*(rl/(r-1)-x)2]
D29. Jaką pracę należy wykonać, aby między okładki płaskiego kondensatora o pojemności C wsunąć elektrycznie obojętną metalową płytę o powierzchni równej powierzchni kondensatora? Odległość między okładkami kondensatora wynosi d a grubość płyty g. Rozpatrzyć przypadki: a) kondensator jest podłączony ze źródłem napięcia U, b) kondensator naładowany do napięcia U jest odłączony od źródła.
_______ W1=1/2*C1U2 gdzie C1=s(d - g) |d| ____ praca wykonana __ W=W1-Wo=1/2*CoU2(C1/Co-1)= U =1/2*CoU2[d/(d - g) - 1]=
=1/2*CoU2(g/(d - g)) b) źródło odłączone (Q=CoU=const) stąd W1=Q2/2C1=Co2U2/2C1 praca W=W1 - Wo=1/2*CoU2(Co /C1 -1)=1/2*CoU2((d -g)/d -1)= =1/2*CoU2((d -g -d)/d)= -1/2*CoU2(g/d) D30. Korzystając z zasady superpozycji oddziaływań obliczyć potencjał pola elektrycznego wytworzonego przez dipol elektryczny w odległości r od środka dipola: a) na symetralnej odcinka łączącego obydwa ładunki b) na prostej łączącej obydwa ładunki. a) _______l______ k(+q)/r+k(-q)/r=0 -q | +q r | r
A b) -q_____________+q _ _ _ _ _ _ B moment dipolowy |_________________| r B=k*(q/(r -l/2))+k*( -q/(r+l/2))=kq[1/(r -l/2) -1/(r+l/2)]= =q/4o*((r+l/2 -r+l/2)/(r2 -l2/4))=ql/4(r2 -l2/4) lub B=pe/4(r2 -l2/4)
D31. W zewnętrznym polu elektrycznym, o stałym kierunku wektora tak że tworzy on z liniami sił pola kąt =60o . Obliczyć:
a) moment siły działającej na dipol w przypadku, gdy zewnętrzne pole elektryczne było jednorodne, a jego natężenie
b) siłę wywieraną na dipol w przypadku, gdy zewnętrzne pole elektryczne charakteryzowało się stałym gradientem:
(zakładamy, że pole było skierowane wzdłuż osi OX).
a) siły odziaływania na dipol tworzą moment siły, który stara się obrócić dipol
M=F*(l/2)+F*(l/2)=F*l=E1ql=E1pe czyli M=E*sin*pe lub M=peEsin
pe=5[C*m] E=2*103[N/C] M=5 b) wypadkowa siła wynosi F=F+-F-=qE1-qE2 przy czym E1-E2=(E/x)*l czyli F=ql(E/x)= pe(E/x)=5[C*m]*2[N/(C*m)]=10[N]
D92 (128) Obliczyć logarytmiczny dekrement drgań tłumionych wahadła o długości l=50 cm, jeżeli w ciągu 8 minut wahań traci ono 99% swojej energii.
Energia wynosi: oraz
czyli
D85 Wyobraźmy sobie szyb przecinający na wskroś kulę ziemską wzdłuż średnicy. Podać równanie ruchu ciała, które wpadło w ten szyb, biorąc pod uwagę zmienną wartość siły ciężkości wewnątrz Ziemi. Obliczyć czas w ciągu którego ciało osiągnie środek Ziemi oraz prędkość z jaką go minie Przy założeniu, że gęstość Ziemi jest stała siła działająca na ciało we wnętrzu Ziemi jest wprost proporcjonalna do jego odległości od środka Ziemi. Rozw Ponieważ oddziaływanie zewnętrznej powłoki znosi się to siła działająca na ciało w odległości x od środka Ziemi wynosi
F(x)=GM(x)m/(x*x) gdzie M(x)=ro
F®=GM®m/(R*R)=mg gdzie M®=ro4/3
Możemy powiedzieć o tym rucu harmoniczny i otzymujemy równanie ruchu |
D83 Jeżeli wagon jest w spoczynku to częstotliwość drgań wahadła matematycznego znajdującego się w tym wagonie wynosi f=0.5Hz. Oblicz częstotliwość drgań tego wahadła w wagonie poruszającym się po torze poziomym z przyspieszeniem a=4.9m/(s*s). Płaszczyzna drgań wahadła jest równoległa do kierunku ruchu wagonu. Przyspieszenie ziemskie g=9.8m/(s*s).
Rozw Łatwo wykazać, że okres drgań wahadła mat o długości l wyraża się wzorem
D84 Okres wahań matematycznego wahadła wykonanego z nieprzewodzącej nici i małej kulki o masie m=25g wynosi
Rozw okres drgań wahadła wynosi
stąd D85 Wyobraźmy sobie szyb przecinający na wskroś kulę ziemską wzdłuż średnicy. Podać równanie ruchu ciała, które wpadło w ten szyb, biorąc pod uwagę zmienną wartość siły ciężkości wewnątrz Ziemi. Obliczyć czas w ciągu którego ciało osiągnie środek Ziemi oraz prędkość z jaką go minie Przy założeniu, że gęstość Ziemi jest stała siła działająca na ciało we wnętrzu Ziemi jest wprost proporcjonalna do jego odległości od środka Ziemi. Rozw Ponieważ oddziaływanie zewnętrznej powłoki znosi się to siła działająca na ciało w odległości x od środka Ziemi wynosi
F(x)=GM(x)m/(x*x) gdzie M(x)=ro
F®=GM®m/(R*R)=mg gdzie M®=ro4/3
Możemy powiedzieć o tym rucu harmoniczny i otzymujemy równanie ruchu FALE D.40Prędkość fazowa fal o długości λ rozchodzących się na powierzchni wody przy pominięciu napięcia powierzchniowego wyraża się wzorem
gdzie g jest przyspieszeniem grawitacyjnym. Wykazać, że prędkość grupowa jest równa 0.5 prędkości fazowej.
D41.Napięcie na okładkach kondensatora w obwodzie drgań elektrycznych LC zmienia się według równania U=50cos(10^6Πt); C=20pF; (? T,L,Q0,λ?);
D42.Ucho ludzkie może odbierać dźwięki o częstotliwościach 20 do 20000 Hz. Między jakimi długościami fal jest zawarty przedział słyszalności ? Prędkość dźwięku w powietrzu przyjąć 340 m/s. Oko ludzkie może odbierać fale świetlne o długościach 380 - 760 nm. Znaleźć odpowiadający temu przedziałowi długości fal świetlnych przedział częstotliwości. PR. Światła 3*10^8 m/s.
ZASADA ZACHOWANIA PĘDU Zad.59 Od dwustopniowej rakiety o masie M=1200 kg po osiągnięciu szybkości v=200 m/s oddzielił się pierwszy stopień o masie m=700 kg . Jaką szybkość osiągnął drugi stopień rakiety, jeżeli szybkość pierwszego stopnia zmalała w wyniku tej operacji do v1=150 m/s? Dane : M=1200 kg; v=200 m/s; m=700 kg; v1=150 m/s; Szukane: v2=? Z zasady zachowania pędu: v*M=v1*m+v2*(M-m) Przekształcając wzór mamy: v2=(v*M-v1*m)/(M-m) Odp.: v2=270 m/s Zad.60 Granat lecący w pewnej chwili z prędkością v=10 m/s rozerwał się na dwa odłamki. Większy odłamek, którego masa stanowiła p=60% masy całego granatu, kontynuował lot w pierwotnym kierunku, lecz ze zwiększoną prędkością v1=25 m/s. Znaleźć kierunek i wartość prędkości mniejszego odłamka. Dane: v=10 m/s; p=60%; v1=25 m/s; Szukane: v2=? Pęd większego odłamka jest równy pędowi mniejszego odłamka: p*(v1-v)=(1-p)*(v2+v); Po przekształceniach mamy v2=(v1-v)*p/(1-p)-v Odp.: v2=12,5 m/s Zad.61 Masa startowa rakiety (z paliwem) wynosi m1=2 kg . Po wyrzuceniu paliwa o masie m2=400 g rakieta wznosi się pionowo na wysokość h=1000 m. Oblicz prędkość wyrzuconego paliwa. Dane: m1=2kg; m2=400 g=0,4 kg; h=1000 m; Szukane: v2=? Energia kinetyczna wyrzucanego paliwa zamienia się w energię potencjalną rakiety: Ek=v2*v2*m/2; Ep=(m1-m2)*g*h; Ek=Ep; v2*v2=2*(m1-m2)*g*h/2;
Odp.: v2=200* Zad.62 Na nieruchomej łodzi o masie m0 stoi dwóch ludzi o masach m1 i m2. Jeden na dziobie, drugi na rufie. W pewnej chwili skaczą oni z prędkościami względem łodzi odpowiednio u1 i u2. Kierunki ich prędkości leżą na osi łodzi a zwroty są przeciwne. Opisz zachowanie się łodzi zaniedbując opór wody. Dane: m0, m1, m2, u1, u2; Szukane: v łodzi; Z zasady zachowania pędu: 0 - pęd przed skokami; m1*u1 - pęd pierwszego człowieka; -m2*u2 - pęd drugiego człowieka ( z minusem bo zwrot prędkości jest przeciwny ); m0*v - pęd łodzi; Z tego mamy 0=m1*v1-m2*v2+m0*v; czyli: v=(m2*v2-m1*v1)/m0; Zakładając, że skaczą oni w kierunku środka łodzi to jeżeli m2*v2>m1v1 to łódź popłynie do tyłu, jeżeli m2*v2<m1*v1 to łódź popłynie do przodu, jeżeli m2*v2=m1*v1 to łódź pozostanie nieruchoma. Pomijając opory wody zgodnie z I zasadą dynamiki Newtona łódź wprawiona w ruch z prędkością v będzie się cały czas z tą prędkością poruszała, aż do napotkania oporu ruchu. Zad.63 Poruszające się ciało o masie m1 zderza się z ciałem nieruchomym o masie m2. Uważając zderzenie za idealnie niesprężyste i centralne, oblicz jaka część ε początkowej energii kinetycznej Ek1 zamienia się na ciepło. Zadanie to rozwiąż najpierw w postaci ogólnej a następnie w przypadku: a) m1=m2; b) m1=9*m2 Dane: m1,m2; Szukane: ε; v1 - prędkość ciała o masie m1; v2 - prędkość układu ciał o masie m1+m2; Z zasady zachowania pędu: m1*v1=(m1+m2)*v2; z tego v2=m1*v1/(m1+m2); Energia przed zderzeniem - Ek1=m1*v1*v1/2+m2*0*0/2 ( prędkość pierwszego ciała = v1, prędkość drugiego ciała = 0 ); Ek1=m1*v1*v1/2; Energia po zderzeniu Ek2=(m1+m2)*v2*v2/2; Energia przeznaczona na ciepło podczas zderzenia Ec=Ek1-Ek2=Ek1*m2/(m1+m2); Z tego ε=Ec/Ek1=m2/(m1+m2); a) dla m1=m2 ε=1/2; b) dla m1=9*m2 ε=1/10 Zad.64 Ciało o masie M spada z wysokości H. W połowie wysokości zostaje trafione poziomo lecącym pociskiem, który wbija się w nie niesprężyście. Masa pocisku wynosi m=0,1*M, a jego prędkość wynosi v. Obliczyć prędkość układu w momencie upadku na ziemię. Dane: M, m, H, v; Szukane vk - prędkość układu w momencie upadku; Prędkość pionowa w dół wynosi s=g*t*t/2; t=v/g; s=v*v/(2*g); Z tego
Prędkość pozioma do połowy drogi jest równa 0. W wyniku uderzenia rośnie do prędkości vx. Z zasady zachowania pędu w kierunku poziomym: M*0+m*v=(M+m)*vX; Z tego vX=m*v/(M+m);vX=m*v/(11*m); vX=v/11; Ponieważ wektory vX i vY są prostopadłe do siebie, to wartość:
SIŁA BEZWŁADNOŚCI D33. Rowerzysta jedzie ze stałą prędkością v=10 m/s po torze kołowym. Kąt nachylenia płaszczyzny roweru do poziomu wynosi α=30°. Oblicz promień toru.
D36. Pocisk wystrzelono z prędkością początkową v0=1000 m/s skierowaną pod kątem α=60° do poziomu z działa skierowanego na południe znajdującego się na półkuli północnej w miejscu o szerokości geofraficznej ϕ=60°. Obliczyć odchylenie pocisku od linii strzału w chwili upadku. Okres obrotu Ziemi T=86201s.
POLE MAGNETYCZNE PRZEWODNIKA Z PRĄDEM D32 - Znaleźć indukcję pola magnetycznego do prądu I, który wpływa z punktu O i rozchodzi się radialnie po nieskończonej płaszczyźnie XOY. Nie umie przeczytać tego zadania z ksera a poza tym w książce wyszedł inny wynik. D33 - Przez dwa długie, cienkie, współosiowe cylindry przewodzące o promieniach R1 i R2 > R1, płynie w kierunkach przeciwnych prąd o natężeniu I. Znaleźć rozkład wektora indukcji w przestrzeni. Zgodnie z tw. Ampera:
dla rozpatrywanego przypadku: dla 0<r<R1 nie ma żadnych prądów wewnątrz zatem H=0 dal r>R2 H2πr=+I-I=0 czyli H=0 dla R1<r<R2 H2πr=I czyli H=I/(2πr)
D34 - Załóżmy, że indukcja pola magnetycznego wewnątrz długiego przewodnika o promieniu R wzrasta proporcjonalnie do czasu B (wektor) = β (wektor) t, natomiast w przestrzeni na zewnątrz przewodnika B (wektor) = 0. Jakie pole elektryczne powstanie w przestrzeni wokół przewodnika? Zakładamy, że pole B (wektor) istnieje wewnątrz przewodnika jest jednorodne i równoległe do jego osi symetrii. W płaszczyźnie prostopadłej do zmiennego pola magnetycznego powstaje wirowe pole elektryczne przy czym na podstawie prawa Maxwella:
czyli:
dla 0<r<R czyli E=-1/2Br (znak wyznacza zwrot wektora E)
dla r>R
D35 - Płaski dysk o promieniu R, naładowany ładunkiem o stałej gęstości powierzchniowej σ, wiruje wokół swej osi z prędkością kątowąω. Znaleźć wektor indukcji magnetycznej w środku dysku Podczas obrotu wąski pierścień o promieniu r i szerokości dr stanowi „nitkę prądową” gdzie w czasie T=(2π)/ω przepływa ładunek dQ=δ2πrdr zaś
prąd ten wytwarza w środku pierścienia pole magnetyczne o indukcji:
zatem IDUKCJA ELEKTROMAGNETYCZNA D36 - Pręt o długości l i masie m położono na dwóch szynach nachylonych pod kątem α do poziomu. Szyny znajdują się w polu magnetycznym o indukcji B, której wektor ma kierunek pionowy w dół. Obliczyć maksymalną prędkość vm jaką może uzyskać pręt, gdy szyny są zawarte na końcu oporem R. Współczynnik tarcie pręta o szyny wynosi f.
Ponieważ strumień przenikający przez kontur obwodu wynosi ΦB=BPlx (Bp=Bcosα) to wytwarza się SEM indukcji Wówczas pojawi się siła elektrodynamiczna przeciwdziałająca zsuwaniu się pręta FL=-BpJl gdzie I=E/R zatem FL=(B2cos2 αl2v)/R
D37 - Zwój w kształcie płaskiej ramki o powierzchni S =5cm2 i oporze R1=2Ω jest połączony z galwanometrem balistycznym o oporze R2=48Ω. Zwój znajduje się jednorodnym polu magnetycznym o indukcji B=0.2T, przy czym płaszczyzna ramki jest prostopadła do linii sił. Jaki ładunek popłynie przez galwanometr, jeżeli ramka zostanie obrócona o kąta =180°? Gdy ramkę obracamy od α=0° do α=90° popłynie prąd przeciwdziałający zmniejszaniu się strumienia magnetycznego w kierunku zgodnym z ruchem wskazówek zegara
przy czym I=ΔQ/Δt ΦB0=BS, ΦB1=0 czyli:
przy obrocie od kąta α=90° do α=180° strumień narasta i wtedy kierunek prądu zmienia się na przeciwny a przez obwód popłynie identyczny ładunek ΔQ=2*10-6 C w kierunku przeciwnym.
D86 (121) Na gumce o długości l i promieniu r wisi odważnik o masie m. Wiedząc, że moduł Younga dla tej gumy jest równy E znaleźć okres drgań odważnika.
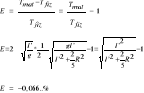
D87 (122) Na cienkiej nici o długości l zawieszono kulę o promieniu R=0.1l. Wyznaczyć błąd względny E, jaki zostanie popełniony przy obliczaniu okresu drgań, jeśli potraktuje się ten układ jako wahadło matematyczne.
Dla wahadła fizycznego:
Błąd względny:
D88 (123) Płytka wykonuje drgania harmoniczne w kierunku poziomym o okresie T=5s. Spoczywający na tej płytce przedmiot zaczyna się poruszać po powierzchni płytki z chwilą, gdy amplituda drgań osiąga wartość A=0.4m. Jaki jest współczynnik tarcia pomiędzy płytką a przedmiotem?
Klocek zacznie się poruszać, gdy:
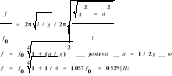
D91 (127) Logarytmiczny dekrement drgań tłumionych wahadła matematycznego równa się δ=0,02. Obliczyć ile razy zmniejszy się amplituda drgań po 100 całkowitych wahnięciach.
Dekrement logarytmiczny tłumienia wynosi δ=βT oraz
dla t=100T
lub D93 (129) Wagon kolejowy o ciężarze Q0=21582N jest zawieszony na 4 resorach. Przy zwiększeniu obciążenia o Q1=9810N resor ugina się o s=0,016m. Dla jakiej prędkości pociągu mogą wystąpić rezonansowe drgania wagonu pod wpływem uderzeń kół o złącza szyn? Długość szyn l=12,5m. Aby doszło do rezonansu, okres uderzeń kół o łączenia szyn musi być równy okresoei drgań własnych wagonu.
natomiast
Ponieważ wagon uderza o szyny po przebyciu drogi l będące j długością szyn to
|
![]()
![]()
![]()
...
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
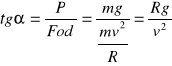
Wyszukiwarka
Podobne podstrony:
zadania z fizyki na kolosy, Studia POLSL, STUDIA, Fizyka, kolokwia
Zadania z dynamiki, Studia, Fizyka, ćwiczenia
Zadania fizyka 1, Studia, pomoc studialna, Fizyka- sprawozdania
granice funkcji-zadania, =====STUDIA, Fizyka Budowli - WSTiP
Zadania z kolosow z lat poprzednich, Studia, pomoc studialna, Fizyka- sprawozdania
budownictow zadania fizyka, Budownictwo-studia, fizyka
Fiza gotowe rozwiazania-sciaga, STUDIA, Fizyka
fiza sciaga, Studia, MECHANIKA I BUDOWA MASZYN, Fizyka
fiza wykład 2 1, Studia, BUD 1 rok, Fizyka
fiza cw 2, Studia, II rok, fizyka
lab fiza 23, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, fizyka1, fiza, Fizyka 2, 23
fiza sciaga, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza
Elektronika 10, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
SEM 2, Studia POLSL, STUDIA, Fizyka, laboratoria, SEM
Sem, Studia POLSL, STUDIA, Fizyka, laboratoria, SEM
Elektronika 08, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
O91B~1, Politechnika Lubelska, Studia, Studia, materiały na studia, Fizyka - Sprawozdania poukładane
FIZA PYT, Studia, Ogólne, Fiyzka, od romka, fizyka all, Fizyka lab, STARE, FU
Fiza all, Studia, EiT semestr-1, Fizyka (starsze roczniki)
więcej podobnych podstron