1 Ruch drgający.

Wahadło sprężyste to układ który zawiera: ciało o masie m + sprężyna o współczynniku sprężystości k.

Rys.

Siła tarcia i oporu wynosi 0.

Rozpatrzmy charakter ruchu pod wpływem siły Hooke'a. Wiadomo że siła Hooke'a jest wprost proporcjonalna do wartości wychylenia X.

F = -kx (1) znak minus oznacza że siła jest skierowana w kierunku przeciwnym do kierunku wychylenia x. Wychylmy teraz ciężar lub ciał o odcinek +x

Rys

Punkt O jest położeniem równowagi w którym wychylenie i siła Hooke'a równa się 0. Na ciężar będzie działać siła Hooke'a skierowana ku położeniu równowagi. Pod wpływem takiej siły ciężar zacznie się poruszać w kierunku równowagi gdy ciężar znajdzie się w położeniu równowagi siła F = 0 ciężar będzie jednak posiadał zapas prędkości V w skutek tego przejdzie położenie równowagi i będzie się poruszać w lewo i zacznie działać siła Hooke'a i będzie hamować ciężar tak długo aż nastąpi zatrzymanie

Rys

Po zatrzymaniu ciężar zacznie się poruszać z powrotem w kierunku równowagi w ten sposób ustali się ruch drgający ciężaru względem punktu równowagi O.

Według I Zasady Newtona siła jest równa F=ma (2).

Podstawiając siłę hooke'a (1) do prawa Newtona mamy

ma = -kx (3).

Wiadomo że przyśpieszenie to druga pochodna wychylenia względem czasu.

Wprowadźmy oznaczenia ω²=k/m

Z punktu widzenia matematyki równanie (6) to różniczka. Rozwiążmy a więc musimy znaleźć związek między wychyleniem x a czasem t x(t). Przypuśćmy, że wychylenie zależy od czasu zgodnie z prawem sinusa x(t)=Asin(ωt+δ) (7).

Znajdując drugą pochodną równania (7) względem czasu przekonujemy się że zmienia ona równanie ruchu (6) w tożsamość dx/dt= Aωcos(ωt+δ) d²x/dt²=-Aω²sin(ωt+δ) (8)

Podstawiając (7) i (8) do (6) mamy:

-Aω²sin(ωt+δ) + ω²Asin(ωt + δ) = 0 ; 0=0

To jest dowód tego że rozwiązanie (7) jest rozwiązaniem równania ruchu (6).

Wyjaśnimy jaki fizyczny sens posiadają wielkości A, ωt + δ

Ze wzoru (7) wynika, że A-max wartość wychylenia (amplituda)

α = ωt + δ -nosi nazwę fazy. Faza to jest kąt który określa położenia punktu drgającego dla dowolnej chwili czasu.

δ-faza początkowa jest to kąt który określa położenie punktu w chwili początkowej t = 0

ω - częstość kątowa [ω] = rad/s

oprócz częstości kątowej można wprowadzić zwykłą częstotliwość √, ω = 2Π√ (9).

√ - częstotliwość to jest liczba drgań w jednostce czasu jest ona związana z okresem √=1/T (10). Okres to czas jednego pełnego drgania.

Wykorzystując wzór ω²=k/m zrobimy obliczenia wartości okresu wahadła sprężystego.

(10) do (9) mamy: ω²=4Π²/T² (11).

Na porównanie k/m=4Π²/T² => T=2Π
(12)

Okres zależy od masy i współczynnika sprężystości

2 DRGANA ELEKTRYCZNE W OBWODZIE LC

Rozpatrzmy obwód składający się z cewki o indukcyjności L i kondensator o pojem C połącz szeregowego

1)

Załóżmy że opór omowy cewki jest tak mały że można go pominąć. Jeżeli do C włączymy na krótki moment baterię która naładuje się do napięcia U_k to na okładzinach C zgromadzi się ładunek Q = U_kC (1)

Po wyłączeniu baterii C zaczyna się rozładowywać i przez obwód płynie prąd I

2)

Prąd elektr płynący przez cewkę wytwarza wewnątrz cewki strumień magnetyczny.

Zmiana natężenia prądu (natężenie prądu rośnie) powoduje również zmiany strumienia magnet w wyniku tego we własnych uzwojeniach cewki pojawiasie SEM samoindukcji

przeciwstawiająca się wzrostowi prądu I zgodnie z prawem Lorentza. Znak „-„ oznacza że siła SEM zawsze skierowana jest przeciw wzrostowi prądu. W momencie kiedy natężenie prądu osiągnie wart max kondensator będzie całkowicie rozładowany

3)

Po rozładowaniu C prąd w obwodzie nie przestaje płynąć ponieważ jest podtrzymywany przez SEM E_s. Prąd ten ponownie ładuje C przy czym powstające między okładkami pole elektrycz ma zwrot przeciwny. Po naładowaniu C ponownie rozładowuje się i ten proces powtarza się lecz w przeciwnym kierunku.

4)

Wnioskujemy, że zjawisko okresowe zachodzące w obw LC nazywamy drganiami elektr, a obwód gen drgań elektr.

Zrobimy oblicz częstości drgań własnych tego obw Wykorzystujemy w tym celu 2 prawo Kirchhoffa:

W dowolnym obw zamkniętym suma algebraiczna SEM zawartych w tym obwodzie równa się sumie iloczynów natężeń prądów i oporów poszczególnych gałęzi obwodu

Zauważmy że w obwodzie I~ do SEM dochodzą nap na okładkach C i uogólnione 2 prawo Kirhchoffa ma postać

Napiszmy 2 prawo Kirhchoffa dla obw LC

Po zróżniczkowaniu czasu mamy

Zgodnie z określeniem

Podst (7) do (6) mamy

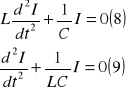
z punktu widzenia matem równanie 9 jest równ różniczkowym i zrobimy porów z równ ruchu wah sprężystego

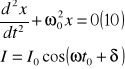
prąd zmienia się zgodnie z prawem sin lub cos

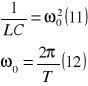
podst (12) do(11) mamy że okres drgań w obw LC wynosi

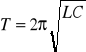
wzór Thomsona

3 DRGANIA TŁUMIONE (GASNĄCE)

Rozpatrzmy drgania wah sprężystego które znajduje się w ośrodku lepkim (siła oporu lub siła tarcia równa się 0). Wiadomo że siła oporu zależy od prędkości ciała i skierowana jest zawsze przeciwnie do kier V i jest wprost proporcjonalna do kier V

gdzie γ współcz oporu

Całk siła działająca na ciało (wah sprężyste) równa się sumie siły oporu i siły sprężystej Q Hooka

wg 2 zas Newtona siła wypad równa

W naszym przypadku

wiadomo że

pods do (4) mamy

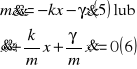
wprowadźmy oznaczenia

mamy

Z punktu widzenia matem równ (70 jest równ różniczkowym. Zauważmy że jeżeli siła oporu = 0 to częstość drgań wynosi _(drgania własne)

Zrobimy rozw równ (7) , dlatego wprowadzimy nową zmienną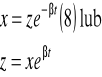

Zróżniczkujemy wzór (8)

różniczkujemy

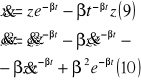
podst (8) (9) (10) do rów (7) mamy

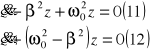
wprowadźmy oznaczenia

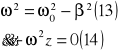
Równ (14) jest identyczne z równ ruchu wah bez oporu . stąd wynika że rozw tego równ ma postać

gdzie A₀ - ampl początk dla t=0

 - częst drgań tłumionych

Ze wzoru (13) wynika że częstość drgań tłumionych jest zawsze mniejsza niż częstość drgań własnych

Wiadomo że
Podst (15) do wzoru (8)mamy, że wychylenie x zależy od czasu w sposób następujący

i jest to rozwiązaniem równ różniczkowego (14)

Wyjaśnijmy jaki fiz sens ma czynnik

ampl drgań tłumionych

Zzyli ampl maleje ze wzrostem czasu t.

Zrobimy wykres zależności (16)

Wprowadźmy pojęcie dekrementu drgań tłumionych:

Log stosunek dwóch kolejnych wart amplitud z których druga następuje po pierwszej w odstępie czasu = T nazywa się dekrementem log tłumienia

Zgodnie z określeniem dekrement ma postać

podst wart amplit (17) mamy

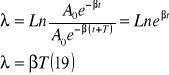
4 Drgania elektryczne w obwodzie RLC

W taki sam sposób jak w LC zachodzą drgania elektryczne w RLC, ale w skutek straty energii (w postaci ciepła na oporze R) drgania te są drganiami tłumionymi.

II prawo Kirchhoffa dla dowolnej chwili czasu

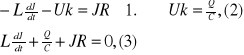
Po zróżniczkowaniu względem czasu mamy

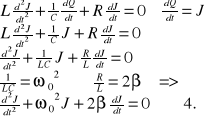
Zrobimy porównanie z równaniem ruchu wahadła w lepkim ustroju: drgania tłumione

Z porównania wynika, że równanie ma postać:

W obwodzie RLC wartość prądu maleje ze wzrostem czasu. Mamy drgania gasnące. Jo - maksymalna wartość natężenia prądu przy czym częstotliwość drgań tłumionych wynosi :

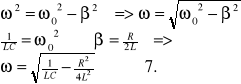
Logarytmiczny dekrement tłumienia dla obwodu RLC

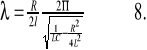
5. Drgania wymuszone

Rozpatrzmy drgania wykonywane przez punkt materialny w warunkach gdy oprócz sił sprężystości i sił oporu działa na niego dodatkowa siła okresowo zmienna.

Załóżmy, że ta dodatkowa siła wymuszająca zmienia się w zależności od czasu według prawa sinusa.

Fw = P cos t (1)

Wielkość p jest największą wartością tej siły

F_s = -kx (2) Siła sprężystości

F_op = -γV (3) siła oporu

Punkt drga wzdłuż osi X

Wedłóg II zasady dynamiki Newtona siła wypadkowa

F =ma (4) w naszym przypadku

F = -kx - γV + Fw (5)

Podstawiając (5) do (4) -kx -γV + Fw = ma

(6) Rownanie ruchu pktu materialnego

Z punktu widzenia matematyki równanie (7) jest równaniem różniczkowym. Zauważmy, że jeżeli nie występuje siła wymuszająca  = 0 oraz siła oporu  = 0 to częstość drgan punktu materialnego wynosi _

_ jest częstością drgań własnych układu.

Rozwiązanie tego równania ma postać

X = A cos (t + δ ) (8) ale amplituda drgań wymuszonych zależy od częstości siły zewnętrznej (1) mianowicie amplituda

Faza początkowa δ

tgδ =

11a. Zjawisko rezonansu

Z równania (9) wynika, że amplituda drgań wymuszonych zależy od stosunku częstości  (siły wymuszającej) i częstości _ drgań własnych. Jeżeli częstość  siły wymuszającej zmienia się a częstość _o drgań własnych pozostaje stała, to będzie się zmieniać amplituda drgań wymuszonych. Według wzoru (9) znajdziemy A max amplitudy drgań wymuszonych.

Aby się o tym przekonać należy znaleźć minimum mianownika w (9) w tym celu pochodną mianownika przyrównujemy do zera

Z = (_o²-²)² + 4² ²

1.wartość  = 0 nie posiada sensu fizycznego

² = _o ² - 2² =>

mianownik (9) osiąga minimum gdy
maksimum amplitudy ze wzoru (9) drgań wymuszonych występuje wówczas gdy częstość siły wymuszającej jest

Zrobimy wykres zależności (9)

Określenie

Zjawisko ostrego powiększenia amplitudy drgań nazywa się zjawiskiem rezonansu.

Widzimy, że im większy jest współczynnik tłumienia  to tym ostrzej zarysowuje się Maximum amplitudy. W wypadku gdy opór ośrodka =0 (=0) maksimum amplitudy będzie występować gdy  = ₀ (12) tzn. wówczas gdy częstość  siły wymuszającej stanie się równe częstości drgań własnych ₀ nastąpi zjawisko rezonansu

W tym przypadku zgodnie z równaniem (9) amplituda drgań stanie się nieskończenie wielka.

Zjawiska rezonansu odgrywają dużą rolę w procesach fizycznych oraz w radiotechnice, przy czym występowanie rezonansu w pewnych przypadkach jest szkodliwe np. silnik(częstość obrotów) i jego podstawa gdy wejdą w rezonans może dojść do uszkodzenia

6 Drgania Elektryczne wymuszone w obwodzie RLC.

Rozpatrzmy drgania elektryczne w obwodzie RLC gdy oprócz elementów RLC obwód zawiera dodatkowo siłę elektromotoryczną okresowo zmienną. Załóżmy, że SEM zmienia się w zależności od czasu według prawa sinusa

Ez = Emax sin t (1)

Wykorzystajmy uogólnione prawo Kirchoffa dla obwodu

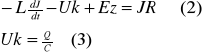
Podstawiając (1)(2)(3) otrzymujemy

Zróżniczkujemy dodatkowo równanie względem czasu

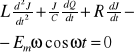
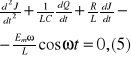
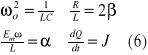
podstawiając (6) do (5) otrzymujemy

równanie (7) jest rónaniem drgań wymuszonych elektrycznych w obwodzie RLC. Zauważmy , że jeżeli nie występuje SEM =0 oraz opór omowy =0 to częstość drgań elektrycznych wynosi
drgania własne.

Z równania drgań wymuszonych punktu materialnego

oraz

z tego porównania wynika, że rozwiązanie równania różniczkowego (7) można zrobić w taki sam sposób jak rozwiązanie równania punktu materialnego. Rozwiązanie ma postać

J=J_o cos (t = δ) (9)

Natężenie prądu jest równe

Zgodnie z (9) z paragrafu 1 faza początkowa

Zrobimy obliczenia wartości amplitudy natężenia prądu Jo Wykorzystując

Podstawiając dane oznaczenia do (10) otrzymujemy

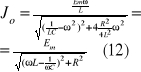
(12) Prawo ohma dla prądu zmiennego.

Znajdźmy max wartość natężenia prądu Jo Mianownik osiąga wartość minimalną w warunkach gdy :
Stąd wynika, że zjawisko rezonansu (ostrego powiększenia amplitudy Jo natężenia prądu nastąpi gdy częstość SEM

częstość SEM = częstość drgań własnych

Max wartość amplitudy Jo wynosi

Przy rezonansie maksymalne natężenia prądu są kilkaset razy większe niż Jo Te zjawisko można wykorzystać dla odbioru potrzebnej częstotliwości.

7. SUPERPOZYCJA DRGAŃ O JEDNAKOWYM OKRESIE (WZDŁUŻ JEDNEJ PROSTEJ)

Przypuśćmy, że punkt materialny wykonuje jednoczesne drgania wzdłuż tej samej prostej(osi OX). Występuje wówczas nakładanie się, czyli superpozycja drgań. Załóżmy, że oba drgania mają ten sam okres T, lecz różne amplitudy i fazy tzn.

(1),

(2).

Wychylenie X ruchu wypadkowego jest sumą wychyleń ruchów składowych, a mianowicie X=X₁+X₂ (3). (1) i (2) do (3) mamy

(4)

wykorzystując wzór cos (A + B) = cosAcosB - sinAsinB mamy

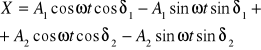
wprowzdźmy oznaczenia

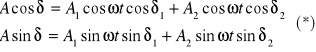
(5).

Wnioskujemy: Mamy, że (5) ruchu wypadkowego jest równaniem ruchu harmonicznego o amplitudzie A i fazie początkowej δ. Zrobimy obliczenia wartości amplitudy A oraz fazy początkowej δ drgania wypadkowego, (5) dlatego wykorzystamy oznaczenie (*).

(6) Podniesiemy do kwadratu i złożymy stronami

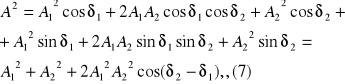
Dla stałej różnicy faz δ₂ - δ₁ drgania są synchroniczne i spójne. Rozpatrzmy szczególny przypadek, kiedy różnica wielokrotności równa się 2Π, a mianowicie różnica faz δ₂ - δ₁ = 2Π gdzie n=0,1,2,…

Ze wzoru (7) wynika, że A=A₁+A₂ (8)

(9)

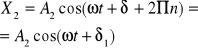
(10).

Zrobimy wykres zależności (9) i (10) i drgania wypadkowego:

8 SUPERPOZYCJA DRGAŃ O RÓŻNYCH OKRESACH (WZDŁUŻ JEDNEJ PROSTEJ)

Rozpatrzmy nakładanie się drgań o różnych okresach T1,T2. Załóżmy dla uproszczenia, że fazy początkowe drgań równają się 0.

Wychylenie X ruchu wypadkowego jest sumą wychyleń ruchów składowych, a mianowicie X=X₁+X₂ (3).

1. i (2) do (3)

2. 
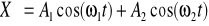
   (4)

Przypuśćmy T1<T2 tzn. >. Dodając i odejmując od prawej strony (4) wyraz

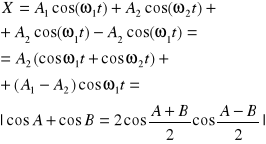
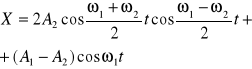
(5)

Wnioskujemy, Ruch wypadkowy nie jest harmoniczny. Np. T1 i T2 mało się różnią
(6)

Wówczas otrzymujemy drgania modulowane.

II. Rozpatrzmy dodawanie dwu drgań o jednakowych amplitudach A1=A2=A0
(7)

gdzie A wypadkowe
(8)

Wiadomo, że A jest dodatnie, dlatego wykorzystano bezwzględną wartość cos, a częstość zmiany drgania wypadkowego równa jest różnicy drgań składowych. Wtedy wychylenie wypadkowe równa się
(9).

Wg założenia, że  różni się mało od  to >>. Drgania wypadkowe (9) można traktować w pierwszym przybliżeniu jako ruch harmoniczny
. Wykres

Widać, że amplituda okresowa zmienia się powoli zgodnie z równaniem osi. Zjawisko to nazywamy dudnieniem. Dudnieniem są drgania o modulowanej amplitudzie, przy czym głębokość modulacji wynosi 100%.

9.Fale.

Przypuśćmy, że punkt drgający znajduje się w ośrodku, którego cząsteczki są ze sobą związane, wówczas energia drgania punktu może być przekazywana otaczającym go punktom i wykonywać ich drgania.

Def.1. Proces rozchodzenia się drgań w ośrodku nazywa się falą.

Np: jeżeli jednemu z końców sznurka, którego drugi koniec jest zamocowany na dany ruch drgający to drganie będzie się przenosić po sznurku, czyli wzdłuż niego pobiegnie fala.

Def.2. Jeżeli drgania cząsteczki i wychylenie się drgań zachodzi wzdłuż kierunku prędkości to falę nazywamy podłużną.

Def.3. Jeżeli drgania cząsteczki są prostopadłe do kierunku prędkości falę nazywamy poprzeczną.

Schemat rozchodzenia się fali poprzecznej.

1. Wykres przedstawia położenie cząsteczki w chwili początku t = 0, gdy wszystkie cząsteczki znajdują się w położeniu równowagi do skaczącej cząsteczki t przyłożono się zew.

2. wykres daje położenia cząsteczek po upływie czasu równego ½ okresu punktu A w tym momencie przechodzi przez położenie równowagi wychylenie równe 0, punkt B osiąga max. Wychylenie

3. Wykres przedstawia położenie cząsteczek po upływie czasu równego okresowi przy czym cząsteczka A przechodzi znów w położenie równowagi ale w innym punkcie, cząsteczka B osiąga max. wychylenie ku dołowi. W ten sposób można obserwować dalsze rozchodzenie się fal.

Wykres rozchodzenia się fali podłużnej.

1. . . . . . .

2. …. . . . .

3. . . ….. . .

4. . . . …….

Wykaż, ze w przypadku fal podłużnych obserwujemy zbliżanie i oddalanie wzajemne cząsteczek, wskutek czego w środku powstaje zagęszczenia i rozchodzenia.

Odradzają własności sprężyste ośrodka zależy czy fale rozchodzące się są falami podłużnymi czy poprzecznymi.

W cieczy i w gazie rozchodzą się tylko fale podłużne.

W ciałach stałych powstać zarówno fale poprzeczne jak i fale podłużne.

Prędkość rozchodzenia się fal zależy: od rodzaju substancji np.: prędkość rozcodzenia się fal podłużnych równa się

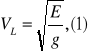
long

gdzie E - moduł Younga, g - gęstość

Prędkość rozchodzenia się fal poprzecznych równa się

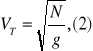
T - trans

N - moduł sztywności

Długość fali jest najmniejszą odległością między drgającymi punktami znajdującymi się w jednakowych fazach.

Np.: dla fali poprzecznej, która rozchodzi się wzdłuż osi y i wysokości x.

Przez rozchodzenie się fali należy rozumieć prędkość rozchodzenia się fazy (prędkość fazowa). Wobec tego faza początkowa w ciągu czasu równego T przebiega odległość równą długości fali λ.

Otrzymujemy v = λ/T (3)

Lub v = λ v v- częstotliwość

Przypuśćmy, że punkt drgający znajduje się w ośrodku ciągłym i drgania rozchodzą się z koła punktu na wszystkie strony. Miejsce geometryczne punktu do których dochodzą drgania nazywamy czołem fali.

Jeżeli ośrodek jest izotropowy (właściwości nie zależą od kierunku) to drgania wychodzące z ośrodka drgań rozchodzą się jednakowo we wszystkie strony. W tym przypadku czoło fali jest powierzchnia kuli

Kształt czoła fali określa typy fali

Np. falą płaską nazywamy falą, której czoło jest płaszczyzną

Fala kulista płaska

Równanie fali płaskiej

Rozpatrzmy falę biegnącą wzdłuż jednej prostej np. wzdłuż osi X.

Oznaczmy X wychylenie punktu z położenia równowagi

X = f * ( l,y)

Proces falowy jest znaczny, jeżeli wartości x każdego punktu prostej, wzdłuż której rozchodzi się fala są w każdym momencie czasu znaczne. Innymi słowy należy znać wychylenie x punktu jako funkcje czasu i współrzędne y.

0 - jest środkiem drgań lub źródłem i drganie zachodzi w tym punkcie według wzoru.

X = A cos ωt (1)

Weźmy dowolny punkt B leżący na linii prostej w odległości y od początku układu. Drgania rozchodzą się z punktu 0, dojdą do punktu B po upływie czasu T

T = y/v (2)

Wobec tego punkt B zacznie drgać o T później niż punkt 0. To znaczy, że pkt. B w chwili dojścia do niego fali zacznie drgać z częstością ω i amplitudą A.

Wychylenie X punktu B z płożenia można wyrazić wzorem: x = A cos ω (t - T) (5)

Podstawiając (2) do (5) mamy:

x = A cos ω ( t - y/v ) (6). Równanie fali płaskiej rozchodzące się w kierunku x.

W tym przypadku dowolna płaszczyzna prostopadła do osi Y jest czołem fali.

Równanie fali płaskiej można przedstawić w następujący sposób: x = A cos 2Π (vt - vy/v) (7)

v = λ v (8), v/v = 1/λ (9).
(9) do (10)

x = A cos 2Π (vt - y/ λ) (10)

x = A cos (ωt - ky) (11); k = 2Π/ λ k-liczba falowa (12)

10.FALE STOJĄCE

Są wynikiem nałożenia się dwóch spotykających się fal płaskich o jednakowych amplitudach. Przypuśćmy że dwie fale płaskie o jednakowych amplitudach rozchodzą się: jedna w kier. dodatniej osi Y, a druga w kier. ujemnej osi Y. Obie fale można przedstawić następującymi równaniami:

Równanie fali płaskiej wzdłuż dodatniej osi Y ma postać:

Równanie fali biegnącej wzdłuż ujemnej osi Y:

suma tych fal równa się

x₁+x₂=x (3)- wychylenie wypadkowe

podst (1) (2) do (3)

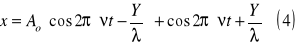
Czynniki cos2t wskazuje na to że w p ośrodka powstaje drganie o częstości równej częstościom spotykających się fal.

Czynnik
nie zależy od czasu i reprezentuje amplitudę drgania wypadkowego

Zauważmy że amplituda jako wielk w zasadzie dodatnia równa się wart bezwzględnej tego czynnika

Drgania wg (6) nazywa się falą stojącą

Zgodnie ze wzorem (7) amplituda fali stojącej zależy od Y. widać że w określ p Y amplituda fali stojącej równa się sumie amplitud obydwu drgań

A_MAX=2A₀ (8)- gdy cos=1

Punkty takie nazywamy strzałkami, w innych punktach Y amplit wypadkowa równa się 0

A_MIN=0 (9)- gdy cos=0

Takie punkty nazywają się węzłami fali stojącej

Obliczmy współ Y strzałek i węzłów

Dla strzałek

wsp strzałek

amplituda fali w węzłach równa się 0

współ węzła

Równanie różnicowe fali płaskiej

Dla otrzymania rów. róż. wykorzystujemy rów. fali płaskiej w postaci: x = A cos (ωt - ky) (1).

Różniczkujemy równanie (1) dwa razy względem czasu t, i dwa razy względem współrzędnej y.

dx/dt = - A ω sin (ωt - ky)

d²x/dt² = - A ω² sin (ωt - ky) (2)

dx/dy = A k sin (ωt - ky)

d²x/dy² = - Ak² cos (ωt - ky) (3)

Podzielimy stronami (2), (3).

d²x/dt² : d²x/dy² = ω²/k² (4) ω = 2Πv ; k = 2Π/ λ

ω²/k² = λ² v² = v² (5)

Podstawiając (5) do (4) mamy:

d²x/dy² = t/v² d²x/dt² (6) Równanie różniczkowe fali płaskiej.

11. INTERFERENCJA FAL

Po pow wody rozchodzi się fala o dowolnym kształcie, na drodze tej fali postawmy przegrodę z otworem małym w porów z dł falia

Fala po dojściu do przegrody P odbije się od niej, a otwór d stanie się źródłem fal rozchodzących się po drugiej stroni przegrody.

Zjawisko Huygensa

Każdy punkt ośrodka do którego dochodzi czoło fali można traktować jako nowe źródło fali np.: w pewnym momencie czasu t znane jest czoło fali

W pewnum momencie czasu znane jest czoło fali AB

Trzeba skonstruować nowe czoło fali odpow. momentowi t' wykorzystujemy zasadę huygensa. Dlatego trzeba przyjąć że każdy punkt leżący na czole fali AB jest niezależnym źródłem tzw fal elementarnych.

Obwiednia A'B' wszystkich elementarnych pow falowych będzie nowym czołem fali.

Rozpatrzmy raz fale wychodzące z różnych źródeł , w obszarze przenikania się fal ,drgania nakładają się na siebie i zachodzi nakładanie się fal (interferencja). W wyniku czego w jednym miejscy powstaną drgania silniejsze a w innym słabsze.

Zjawisko interferencji zachodzi wówczas gdy drgające z jednakową częstością źródło drgań mają jednakowo skierowane drgania i stałą różnicę faz.

Takie źródła nazywa się koherentnymi, albo spójnymi. Dla fal niespójnych gdy różnica faz szybko się zmienia zjawisko interferencji nie występuje.

Jnterferencja fal akustycznych

SPOSOBY OTRZYMYWANIA SPÓJNYCH ŹRÓDEŁ

Jeden ze sposobów otrzymywania koherentnych lub spójnych źródeł drgań jest następujący:

bierzemy punktowe źródło S z którego rozchodzi się fala sferyczna

Na drodze fali umieścimy przegrodę z dwoma otworami S1 i S2. otwory S1 i S2 stają się zgodnie z zasadą Huygensa niezależnymi źródłami drgań przy czym mają one jednakowe amplitudy i fazy. Po prawej stronie przegrody będą rozchodziły się fale sferyczne.

Rozpatrzmy drgania wypadkowe w pewnym punkcie A oddalonym od źródeł S1 i S2 odpow o odległ R1 i R2 . drgania dochodzące do p A mają równe fazy które zależą od różnicy R1 - R2. Jeżeli drgania źródeł S1 i S2 mają jednakowe drgania to można je przedstawić za pomocą wzoru

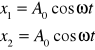
wówczas drgania które dochodzą do p A ze źródeł S1 i S2 można przedstawić w sposób następujący

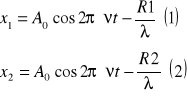
x₁ - wychylenie cząstki drgającej znajdującej się w p A w odległ o R1

x₂ - wychylenie cząstki drgającej znajdującej się w p A w odległ o R2

Jeżeli cząstka bierze udział jednocześnie w obu drganiach wychylenie wypadkowe x można wyrazić jako sumę algebraiczną wychyleń x1 i x2

X = x1 + x2 (3)

12.ZJAWISKO DOPPLERA

Zjawisko Dopplera występuje wtedy, gdy obserwator porusza się względem źródła dźwięku lub źródło dźwięku porusza się względem obserwatora. Polega ono na tym, że obserwator odbiera falę o innej częstotliwości niż częstotliwość drgań źródła np. obniżenie wysokości tonu sygnału samochodowego lub pociągu, gdy nas on mijają.

1) Rozpatrzmy pierwszy przypadek: Źródło dźwięku porusza się wzg. ośrodka z prędkością U. Prędkość rozchodzenia się fal w ośrodku wynosi V. Obserwator jest nieruchomy.

Wiadomo, że prędkość rozchodzenia się fali zależy tylko od właściwości ośrodka np. prędkości fali podłużnej dla powietrza

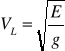
(1) E -wł.sprężyste, g-gęstość

tzn. że w ciągu jednego okresu T rozejdzie się drganie o dł. fali:
(2) niezależnie od tego czy źródło się porusza czy zostaje nie ruchome. Jednak w ciągu czasu T źródło przejedzie drogę S.
(3) w kierunku ruchu fali wobec tego dł., fali
(4)

(2) i (3) do (4) mamy:
(5)

W związku z tym liczba drgań odebranych przez obserwatora w jednostce czasu zwiększy się w skutek skracania się dł. fali.

Częstość odebrana przez obserwatora:

(6)

(5) do (6) mamy:

(7)

Zauważmy gdyby źródło oddalało się od obserwatora U<0 to częstotliwość drgań odebrana od obserwatora była by mniejsza:

2) Rozpatrzmy drugi przypadek. Obserwator porusza się z prędkością U względem źródła, źródło jest nie ruchome.

W tym przypadku koło obserwatora więcej jednostce czasu przebiegnie więcej dł. fal niż w przypadku gdy obserwator nie porusza się wzg. ośrodka. Ten przypadek jest równoważny temu w którym fale przebiegają koło obserwatora z prędkością równą sumie prędkości fali i prędkości obserwatora V+U. Liczba dł. fal przechodzących w jednostce czasu wzg. obserwatora równa się:

(1)
(2)

(2) do (1) mamy:
(3)

W tym przypadku mamy powiększenie częstości

Jeżeli obserwator oddala się od źródła U<0 mamy:

(4)

13.Zasada Huygensa-Fresnela prawa odbicia i załamania fali.

Zgodnie z zasadą H wszystkie punkty czoła fali wysyłają równocześnie kuliste fale elementarne.]

Def.

1. Prosta prostopadła w każdym punkcie do czoła fali nazywa się promieniem fali. Połączenie zasady Huygensa z zasadą interferencji fal elementarnych zostało dokonane przez Fresnela i nosi nazwę zasady H-F.

2. Każdy punkt ośrodka w którym rozchodzi się fala jest źródłem fal elementarnych które w skutek interferencji dają falę obserwowaną.

Za pomocą zasady H-F wyjaśnimy zagadnienia prostoliniowego rozchodzenia się fal np. w jaki sposób fale docierają od punktu 0 do punktu B.

Przypuśćmy że po upływie pewnego czasu czoło fali ma kształt kuli. Zgodnie z metodą F rysujemy kolejne strefy na powierzchni czoła.

Pomiędzy odcinkami AB, CB, DB, EB istnieje związek a mianowicie:

CB=AB+λ/2

DB=CB+λ/2

EB=DB+λ/2 tzn. że różnica dróg pomiędzy kolejnymi strefami F wynosi λ/2.

Rozpatrzmy teraz wyniki interferencji fal elementarnych w punkcie B. Wiadomo że amplituda drgań w wyniku interferencji równa się 0 wówczas gdy różnica dróg równa się nieparzystej liczbie długości półfali.

W naszym przypadku różnice dróg sąsiednich punktów czoła fali (A,C,D..) wynoszą λ/2 wobec czego fale ze stref sąsiednich dają w punkcie B wartość zerową i do punktu B docierają tylko fale z połowy I-szej strefy Fresnela (CAC-I strefa F).

Udowodnimy:

Aw=Ao-Ac+Ad-Ae+...(1)

znak (-) oznacza że amplituda drgań sąsiednich punktów kompensują się.

Aw=Ao/2+(Ao/2-Ac+Ad/2)+(Ao/2-Ae+Ae/2)+....

Aw=Ao/2

Innymi słowy działania całego czoła fali jest więc takie jak działanie połowy I strefy F.

Rozpatrzmy przypadki:

1. fale optyczne (świetlne) długości fali λ∼(0,4÷0,8)μm stąd wynika że rozmiary I-szej strefy F są małe i możemy traktować że światło rozchodzi się wzdłuż linii prostej OB. Inaczej mówiąc można uważać że światło z punktu O do punktu B rozchodzi się po linii prostej.

2. fale głosowe długości fali λ∼1m wobec tego rozmiary I-szej strefy F wynoszą kilka metrów kwadratowych gdy rozmiary przeszkody są porównywalne z długością fali λ fala omija częściowo przeszkodę i nie można mówić o prostoliniowym rozchodzeniu się fali.

Prawo odbicia i załamania fali.

Fala padająca na granicą dwóch ośrodków częściowo odbije się a częściowo przeniknie do drugiego ośrodka.

• Prawa odbicia promieni fal:

1. promień padający promień odbity i normalna do powierzchni granicznej leżą w jednej płaszczyźnie

2. kąt padania równa się kątowi odbicia.

• Prawa załamania promieni fal:

1. promień padający promień załamany i normalna do powierzchni granicznej leżą w jednej płaszczyźnie

2. stosunek sin kąta padania do sin kąta załamania jest wielkością stałą równą współczynnikowi załamania tzn

sinα/sinβ=n (1.)

Wartość n nazywamy współczynnikiem załamania ośrodka 2 względem 1 n21.

Za pomocą zasady H-F zrobimy wyprowadzenie 2 prawa załamania: niech w ośrodku 1 prędkość rozchodzenia się fal wynosi V1 w ośrodku 2 V2.

W czasie τ gdy w 1 ośrodku od punktu A do punktu C przemieści się faza fali padającej z punktu O rozejdzie się fala elementarna na odległości OB.

AC=V1*τ (2.)

OB=V2*τ (3.)

Rozpatrzmy ΔOAC i ΔOCB

AC=OC*sinα (4.)

OB=OC*sinβ (5.)

Podstawiając (4) (5) do (2) (3) mamy:

OC*sinα=V1*τ

OC*sinβ=V2*τ (6.)

sinα/sinβ=V1/V2 (7)

stosunek V1/V2 nazywany jest współczynnikiem załamania n=V1/V2 ośrodka 2 względem 1

• Zasada Farmata:

Droga obrana przez promień fali przy przejściu od jednego punktu do drugiego jest taka że czas potrzebny na przebycie tej drogi jest najkrótszy.

Za pomocą tej zasady zrobimy wyprowadzenie 2 prawa odbicia fal. Niech promień fali wychodzącej z punktu A odbije się od płaszczyzny CD i trafia do punktu B.

C D

Zgodnie z zasadą Fermata w którym promień fali przebywa drogę AOB ma być min. innymi słowy zmianie może ulegać tylko odcinek x tzn. musimy znaleźć położenie punktu O aby czas był min.

T = AO/V + OB/V

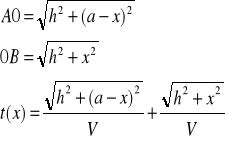
dlatego I pochodna t względem x = 0

dt(x)/dx = 0

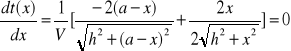
stąd wynika. że

(a-x)2 (h2+x2) = x2 [h2 + (a-x)2]

po opuszczeniu nawiasów

x = a/2

α = β

₂_{222}

₁

A

₁<₂<₃

₃



Jo

₁

₂

₃

_ 

R₁

R₂

R₃

a

t = 0

1) x

B t = T/2

2)

A C x

D t = T

3) A C x

B

X λ

1 2

y

λ

x T t

X

B y

y

st

A

w

w

Y



A

A'

B'

B

S1

R1

R1

A

R2

S2

E

D

C

A B

O C

D

E

F

A V1

α

• 1

β 2

β V2

A B

• β

α β x h

0

a

---