POLITECHNIKA WARSZAWSKA
Wydział Samochodów i Maszyn Roboczych
Projekt: Zamienność selekcyjna.
Paweł Gębal
Gr. 2.3
Warszawa 2009
1. PODZIAŁ NA GRUPY SELEKCYJNE.
a) Cele i kryteria podziału na grupy selekcyjne
Zamienność selekcyjna stosowana jest najczęściej w połączeniach dwóch elementów - wałka i otworu, współpracujących przy określonym pasowaniu. Współpracujące elementy przed montażem mierzy się, po czym dzieli na grupy selekcyjne, przy czym kryterium zaliczenia do odpowiedniej grupy jest zaobserwowany wymiar (odchyłka) elementu. W rezultacie uzyskuje się pasowanie o lepszej jakości, ze zmniejszoną tolerancją pasowania.
Podział przed montażem na n grup selekcyjnych i montaż w grupach zapewnia n-krotne zmniejszenie tolerancji pasowania (a więc takie samo zmniejszenie możliwego rozrzutu wskaźników pasowania, luzu bądź wcisku) według wzoru:
![]()
gdzie: n- liczba grup selekcyjnych.
Dzięki temu wynik montażu będzie taki sam, jak gdyby otwór i wałek były obrobione n razy dokładniej.
Aby podział wyrobów na grupy selekcyjne miał sens praktyczny, liczność odpowiadających sobie grup otworów i wałków powinna być zbliżona. W przeciwnym razie podczas montażu pozostawałyby zbędne części, których nie dałoby się wykorzystać. W tym celu stosujemy podział na grupy o jednakowych tolerancjach.
b) Pasowanie przed selekcją
Typ pasowania 130H7/k6
Wymiar nominalny otworu: ∅ 130mm
Odchyłka dolna otworu: EI = 0,000 mm
Odchyłka górna otworu: ES = +0,040 mm
Wymiar nominalny wałka: ∅ 130mm
Odchyłka dolna wałka: ei = +0,003 mm
Odchyłka górna otworu: es = +0,028 mm
Tolerancja otworu wynosi: To = ES-EI=0,040+0=0,040 mm
Tolerancja wałka wynosi: Tw = es-ei=0,028-0,003=0,025 mm
Tolerancja pasowania: Tp = To+ Tw=0,040+0,025=0,065 mm
Wskaźniki pasowania: Pmin = EI-es=0-0,028=-0,028 mm
Pmax =ES-ei=0,04-0,003= 0,037 mm
Ponieważ:
Pmax>0>Pmin
Dane pasowanie jest, więc pasowaniem mieszanym.
Luz graniczny wynosi: Smax = Pmax= 0,037 mm
Wcisk graniczny wynosi: Nmax = |Pmin|= 0,028 mm
c) Obliczenia
Wałek - rozkład normalny
Pasowanie przed podziałem na grupy selekcyjne wynosiło Tp=0,065mm, zatem po zastosowaniu podziału na 3 grupy, tolerancja pasowania selekcyjna będzie wynosić około Tps=0,0217mm.
Rozkład wymiarów wałka jest rozkładem normalnym o odchyleniu standardowym:
![]()
Oznacza to, że w obszarze 6σ prawdopodobieństwo otrzymania dobrego wyniku wynosi 0,9974.
Metoda empiryczną przyjąłem następujący podział obszaru 6σ na 3 grupy selekcyjne:
1 Grupa selekcyjna: -3σw do -0,6σw
2 Grupa selekcyjna: -0,6σw do +0,6σw
3 Grupa selekcyjna: +0,6σw do +3σw
Wartość średnia:
![]()
Wyznaczenie przedziałów grup selekcyjnych na podstawie zmiennej standaryzowanej:
![]()
Gdzie;
x- dany wymiar
a - średnia
σ - odchylenie standardowe
Pierwsza grupa:
![]()
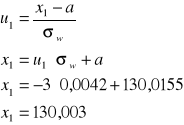
Druga grupa
![]()
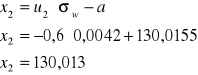
Oraz
![]()
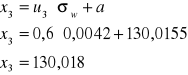
Trzecia grupa
![]()
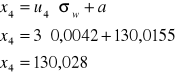
Obliczenia prawdopodobieństwa wystąpienia wymiaru w danej grupie korzystając z funkcji Laplace'a
![]()
Środek rozkładu odpowiada wymiarowi 130,0155.
Pierwsza grupa:
Szukamy prawdopodobieństwa uzyskania odchyłki w przedziale <-0,0125≤X≤-0,0025>.
![]()
Druga grupa:
Szukamy prawdopodobieństwa uzyskania odchyłki w przedziale <-0,0025≤X≤0,0025>.
![]()
Trzecia grupa:
Szukamy prawdopodobieństwa uzyskania odchyłki w przedziale <0,0025≤X≤0,0125>.
![]()
P1+P2+P3=0,9974
Ostateczny podział tolerancji wałka na grupy selekcyjne:
Grupa |
Przedział tolerancji |
Tolerancja grupy [mm] |
Prawdopodobieństwo wystąpienia w grupie |
|
- |
od |
do |
- |
- |
I |
0,003 |
0,013 |
0,010 |
27,29% |
II |
0,013 |
0,018 |
0,005 |
45,16% |
III |
0,018 |
0,028 |
0,010 |
27,29% |
Otwór - rozkład równomierny
Rozkład wymiarów wałka jest rozkładem równomiernym o stałym prawdopodobieństwu.
Rozkład ten w przedziale wymiarów (a, b), gdzie b - a = h > 0, określony jest funkcją postaci:
W naszym przypadku:
a=130,000mm
b=130,040mm
h=0,040mm
p(x)=25 dla x![]()
(130;130,040)
p(x)=0 dla x![]()
(130;130,040)
Aby podział na grupy selekcyjne miał sens liczność wałków i otworów w każdej grupie powinna być zbliżona do siebie, zatem prawdopodobieństwo wystąpienia otworu w danej grupie powinno być takie samo jak wystąpienia wałka tej grupie.
Prawdopodobieństwo wystąpienia wymiaru w danej grupie to pole pod funkcją gęstości prawdopodobieństwa. Można je obliczyć z całki:
![]()
Gdzie:
z - szukany przedział
Dla pierwszej grupy:
![]()
Dla drugiej grupy:
![]()
Dla trzeciej grupy:
![]()
Ostateczny podział tolerancji otworu na grupy selekcyjne:
Grupa |
Przedział tolerancji |
Tolerancja grupy [mm] |
Prawdopodobieństwo wystąpienia w grupie |
|
- |
od |
do |
- |
- |
I |
0,000 |
0,011 |
0,011 |
27,5% |
II |
0,011 |
0,029 |
0,018 |
45% |
III |
0,029 |
0,040 |
0,011 |
27,5% |
Tabela zestawieniowa:
Pasowanie 130H7/k6 |
Przed |
I grupa |
II grupa |
III grupa |
Wymiar nominalny |
D=130 mm ES=+0,040 mm EI=0 mm
|
D=130 mm ES=+0,011 mm EI=0 mm |
D=130mm ES=+0,029 mm EI=+0,011 mm |
D=130 mm ES=+0,040 mm EI=+0,029 mm |
Wymiar nominalny |
D=130 mm es=+0,028 mm ei=+0,003 mm |
es=+0,013 mm ei=+0,003 mm |
es=+0,018 mm ei=+0,013 mm |
es=+0,028 mm ei=+0,018 mm |
Pmax |
0,037 mm |
0,008 mm |
0,016 mm |
0,022 mm |
Pmin |
-0,028 mm |
-0,013 mm |
-0,007 mm |
-0,001 mm |
Charakter pasowania |
mieszane |
mieszane |
mieszane |
mieszane |
Tolerancja pasowania Tp |
0,065 mm |
0,021 mm |
0,023 mm |
0,021 mm |
Prawdopodobieństwo wystąpienia otworu w grupie |
99,74% |
27,29% |
45,16% |
27,29% |
Prawdopodobieństwo wystąpienia wałka w grupie |
100% |
27,5% |
45% |
27,5% |
Wnioski
Dzięki zastosowaniu zmienności selekcyjnej i podziału montowanych elementów na 3 grupy udało się 3-krotnie zmniejszyć tolerancję pasowania selekcyjnego. Dla żadnej z grup nie zmienił się charakter pasowania - pasowanie jest dalej pasowaniem mieszanym. Dzięki przyjętemu podziałowi udało się uzyskać podobną wartość prawdopodobieństwa wystąpienia otworu jak i wałka w danej grupie. W wyniku tego po montażu nie powinny zostać żadne elementy, których nie można już zmontować.
Ograniczenia stosowania selekcji:
Liczba grup selekcyjnych nie może być zbyt duża. Ogranicza ją niedokładność pomiarów wykonywanych w celu podziału na grupy. Przy tolerancji grupy selekcyjnej rzędu 5 mikrometrów niepewność pomiaru nie powinna przekraczać 0,5 mikrometra, co w warunkach produkcyjnych może być wymaganiem trudnym do spełnienia.
Ważniejszym czynnikiem ograniczającym liczbę grup selekcyjnych są odchyłki kształtu. Pole tolerancji kształtu powinno być niewielką częścią pola tolerancji wymiaru.
2.PROJEKT SPRAWDZIANÓW.
a) Obliczenie wymiarów i tolerancji sprawdzianu do otworów ∅ 130H7
Wymiar nominalny otworu: D = 130mm
Odchyłka górna otworu: ES=0,040 mm
Odchyłka dolna otworu EI=0 mm
Wymiar dolny otworu: Ao = D+EI=130,000 mm
Wymiar górny otworu: Bo = D+ES=130+0,040=130,040 mm
Wymiary sprawdzianu ustalam na podstawie normy PN-72/M-02140. zgodnie z zaleceniami tej normy dla danego otworu przyjmuję następujące rodzaje sprawdzianów;
Smin - sprawdzian minimalny przechodni ( o powierzchni pomiarowej walcowej) - sprawdzian łopatkowy walcowy
Smax - sprawdzian maksymalny nieprzechodni ( o powierzchni pomiarowej kulistej) - sprawdzian łopatkowy kulisty
Oznaczenia z norm:
Gz - wymiar granicy zużycia sprawdzianu przechodniego Smin do otworu
H - tolerancja sprawdzianu do otworów o powierzchni pomiarowej walcowej
Hs - tolerancja sprawdzianu do otworów o powierzchni pomiarowej kulistej
Tk - tolerancja kształtu sprawdzianu
Z - odległość pomiędzy osia symetrii pola tolerancji sprawdzianu przechodniego Smin do otworów i linią odpowiadająca wymiarowi dolnemu A otworu
Y - różnica pomiędzy wymiarem dolnym A otworu i wymiarem granicy zużycia Gz sprawdzianu przechodniego Smin do otworu
Z normy odczytuję następujące wartość dla otworu 130H7 no klasie tolerancji IT7.
z=0,006mm
y=0,004mm
Dla sprawdzianu o powierzchni pomiarowej walcowej:
H=0,008 mm
Tk=IT2= 0,005mm
Dla sprawdzianu o powierzchni pomiarowej kulistej:
Hs=0,005mm
Tk=IT1=0,0035mm
Wymiar nowego sprawdzianu przechodniego Smin o powierzchni pomiarowej walcowej:
Smin = (A+z) ±0,5H=(130,000 +0,006) ±0,004=(130,006 ±0,004) mm
Wymiar sprawdzianu nieprzechodniego Smax o powierzchni pomiarowej kulistej:
Smax = B±0,5Hs = 130,040±0,0025 ≅ (130,040±0,003) mm
Wymiar granicy zużycia Gz sprawdzianu przechodniego Smin o powierzchni pomiarowej walcowej:
Gz = A-y=130,000-0,004 =129,996 mm
Tolerancja odbiorcza minimalna Tmin sprawdzianu przechodniego nowego Smin o powierzchni pomiarowej walcowej:
Tmin=(Smax-0,5 Hs)-(Smin+0,5H)=(130,040-0,003)-(130,006+0,004)=130,037-130,010=0,027mm
Tolerancja odbiorcza maksymalna Tmax sprawdzianu przechodniego nowego Smin o powierzchni pomiarowej walcowej:
Tmax=(Smax+0,5 Hs)-(Smin-0,5H)=(130,040+0,003)-(130,006-0,004)=130,043-130,002=0,041mm
Tolerancja odbiorcza minimalna T'min sprawdzianu przechodniego zużytego Smin o powierzchni pomiarowej walcowej:
T'min=(Smax-0,5 Hs)-Gz=(130,040-0,003)-129,996=130,037-129,996=0,041mm
Tolerancja odbiorcza maksymalna T'max sprawdzianu przechodniego zużytego Smin o powierzchni pomiarowej walcowej:
T'max=(Smax+0,5 Hs)-Gz=(130,040+0,003)-129,996=130,043-130,002=0,047mm
Na podstawie powyższych danych rysuję pola tolerancji sprawdzianów na tle pól tolerancji otworu (rys nr 2).
Na podstawie powyższych danych projektuję sprawdzian łopatkowy do otworów (rys nr 5).
Relacje między tolerancjami odbiorczymi, a tolerancją otworu:
Relacja między tolerancja odbiorczą minimalną Tmin sprawdzianu przechodniego nowego, a tolerancją otworu:
![]()
Relacja między tolerancja odbiorczą maksymalna Tmax sprawdzianu przechodniego nowego, a tolerancją otworu:
![]()
Relacja między tolerancja odbiorczą minimalną T'min sprawdzianu przechodniego zużytego, a tolerancją otworu:
![]()
Relacja między tolerancja odbiorczą maksymalna T'max sprawdzianu przechodniego zużytego, a tolerancją otworu:
![]()
b) Obliczenie wymiarów i tolerancji sprawdzianu do wałka ∅ 130k7
Wymiar nominalny wałka: D = 130mm
Odchyłka górna wałka: es=0,028 mm
Odchyłka dolna wałka er=0,003 mm
Wymiar dolny wałka: Aw = D+ei=130,000+0,003=130,003 mm
Wymiar górny wałka: Bw = D+es=130,000+0,028=130,028 mm
Wymiary sprawdzianu ustalam na podstawie normy PN-72/M-02140. Zgodnie z zaleceniami tej normy dla danego wałka przyjmuję następujące rodzaje sprawdzianów;
Smin - sprawdzian minimalny nieprzechodni ( o powierzchni pomiarowej walcowej) - sprawdzian szczękowy
Smax - sprawdzian maksymalny przechodni ( o powierzchni pomiarowej kulistej) - sprawdzian szczękowy
Oznaczenia z norm:
Gz - wymiar granicy zużycia sprawdzianu przechodniego Smax do wałków
H1 - tolerancja sprawdzianu do wałków
Tk - tolerancja kształtu sprawdzianu
z1 - odległość pomiędzy osia symetrii pola tolerancji sprawdzianu przechodniego Smax do wałków i linią odpowiadająca wymiarowi górnemu B wałka
y1 - różnica pomiędzy wymiarem górnym B wałka i wymiarem granicy zużycia Gz sprawdzianu przechodniego Smax do wałka
Z normy odczytuję następujące wartość dla wałka 130k6 o klasie tolerancji IT6.
z1=0,006mm
y1=0,004mm
Dla sprawdzianu szczękowego
H1=0,008 mm
Tk=IT2= 0,005mm
Wymiar nowego sprawdzianu przechodniego Smax szczękowego:
Smax = (B-z1) ±0,5H1=(130,028 -0,006) ±0,004=(130,022 ±0,004) mm
Wymiar sprawdzianu nieprzechodniego Smin szczękowego:
Smin = A±0,5H1 = 130,003±0,004=(130,003±0,004) mm
Wymiar granicy zużycia Gz sprawdzianu przechodniego Smax szczękowego:
Gz = B+y1=130,028+0,004 =130,032 mm
Tolerancja odbiorcza minimalna Tmin sprawdzianu przechodniego nowego Smax szczękowego
Tmin=(Smax-0,5 H1)-(Smin+0,5H1)=(130,022-0,004)-(130,003+0,004)=130,018-130,007=0,011mm
Tolerancja odbiorcza maksymalna Tmax sprawdzianu przechodniego nowego Smax szczękowego
Tmax=(Smax+0,5 H1)-(Smin-0,5H1)=(130,022+0,004)-(130,003-0,004)=130,026-129,999=0,027mm
Tolerancja odbiorcza minimalna T'min sprawdzianu przechodniego zużytego Smax szczękowego:
T'min=Gz-(Smin+0,5H1)= 130,032-(130,003+0,004)= 130,032-130,007=0,033mm
Tolerancja odbiorcza maksymalna T'max sprawdzianu przechodniego zużytego Smax szczękowego:
T'max=Gz-(Smin-0,5H1)= 130,032-(130,003-0,004)=130,032-129,999=0,025mm
Na podstawie powyższych danych rysuję pola tolerancji sprawdzianów na tle pól tolerancji wałka (rys nr 3).
Na podstawie powyższych danych projektuję sprawdzian szczekowy do wałków (rys nr 4).
Relacje między tolerancjami odbiorczymi, a tolerancją wałka:
Relacja między tolerancja odbiorczą minimalną Tmin sprawdzianu przechodniego nowego, a tolerancją wałka:
![]()
Relacja między tolerancja odbiorczą maksymalna Tmax sprawdzianu przechodniego nowego, a tolerancją wałka:
![]()
Relacja między tolerancja odbiorczą minimalną T'min sprawdzianu przechodniego zużytego, a tolerancją wałka:
![]()
Relacja między tolerancja odbiorczą maksymalna T'max sprawdzianu przechodniego zużytego, a tolerancją wałka:
![]()
Tabela Zestawieniowa:
Symbolowe oznaczenie tolerancji |
Otwór H7 |
Wałek k6 |
||
Wymiar nominalny |
D=130 mm ES=+0,040 mm EI=0 mm
|
D=130 mm es=+0,028 mm ei=+0,003 mm |
||
Wymiar nowego |
o powierzchni pomiarowej walcowej |
Smin= =(130,006±0,004)mm |
Smax =(130,022±0,004)mm |
|
Wymiar granicy zużycia Gz |
Gz=129,996 mm |
Gz=130,032 mm |
||
Wymiar sprawdzianu nieprzechodniego |
o powierzchni pomiarowej kulistej |
Smax= =(130,040±0,003) mm |
Smin = (130,003±0,004)mm |
|
Tolerancja odbiorcza |
Sprawdz. nowy |
Sprawdz. zużyty |
Sprawdz. nowy |
Sprawdz. zużyty |
|
Tmin=0,027mm Tmax=0,041mm |
Tmin=0,041mm Tmax=0,047mm |
Tmin=0,011mm Tmax=0,027mm |
Tmin=0,025mm Tmax=0,033mm |
Tolerancja geometryczna powierzchni roboczych sprawdzianu |
Nazwa: a) tolerancja walcowatości Wartość: - powierzchnia pomiarowa walcowa - Tk=IT2=0,005mm b) tolerancja okrągłości - powierzchnia pomiarowa kulista - Tk=IT1=0,0035mm
|
Nazwa: a) tolerancja równoległości Wartość: -powierzchnia pomiarowa płaska - Tk=IT2=0,005mm b) tolerancja płaskości powierzchnia pomiarowa płaska - Tk=IT2=0,005mm
|
||
Chropowatość pow. roboczych |
Ra=0,04 |
Ra=0,04 |
||
Przebieg akceptacji wyrobów:
Tolerancja wyrobu, który może być przyjęty przez sprawdzian, nazywa się tolerancją odbiorczą sprawdzianu. Tolerancja odbiorcza zależy od dokładności wykonania nowego sprawdzianu jak i stopnia jego zużycia. W miarę zużywania się sprawdzianu jego tolerancja odbiorcza będzie rosła na skutek stykania się powierzchni sprawdzianu i przedmiotu sprawdzanego.
W przypadku sprawdzianu łopatkowego do otworów, gdy wymiar minimalny sprawdzianu przechodniego Smin osiągnie wartość nazywana granicą zużycia:
Gz=A-y
to tolerancja odbiorcza T'max sprawdzianu będzie największa. Po przekroczeniu tej wartości sprawdzian nie będzie się nadawał do dalszego użytku.
Podobna sytuacja zachodzi w przypadku sprawdzianów szczękowych do wałków. Gdy wymiar maksymalny sprawdzianu przechodniego Smax osiągnie granicę zużycia określoną zależnością:
Gz=B+y1
To tolerancja odbiorcza T'max sprawdzianu będzie największa. Po przekroczeniu tej wartości sprawdzianu nie będzie już można używać do pomiarów wałków.
Paweł Gębal, gr. 2.3, 130H7/k6, Strona 1 z 15
Wyszukiwarka
Podobne podstrony:
Projekt zamiennośći selekcyjnej, MiBM, Nauczka, 4 semestr, Metrologia, Projekt 2
Projekt metrologia 130h7k6 (praca na 5)(1)
ped praca energia, MiBM, Nauczka, 2 semstr, sesja, Test z fizyki (jacenty86), FIZYKA ZERÓWKA, 4 ped
Mikroekonomia praca na warsztaty, WSEI, semestr 1, Mikroekonomia
7bryla, MiBM, Nauczka, 1 semestr, fizyka, 2011-2012r, Fizyka, fiza
Biznes plan - praca zaliczeniowa, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ekonomia, F
Praca Przejściowa-1, Pomoce Naukowe 2, SEMESTR 6, technologia referat, technologia -projekt
projekt 40 praca na wesoło DMR 1807
Zbior pytan z calego semestru - TW, MiBM, Nauczka, 2 semstr, PNOM, materiałoznawstwo
Ściąga na kolosa z wykładu, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Sem
Odwzorowanie modelu obiektowego na DDL-1, Informatyka, SEMESTR IV, Projektowanie
Pytania na zasady, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 5, S
więcej podobnych podstron