- LOGIKA -
Pojęcie aktu komunikacji i znaku.
Znak - jest to dowolny przedmiot lub zjawisko fizyczne, które służy do zakomunikowania komuś czegoś wobec obowiązywania pewnych konwencji dotyczących zasobu jego rozumienia, np. słowo jest znakiem
Właściwości znaku:
zawsze dostrzegalny zmysłowo
jest trwały (słowo pisane) lub nietrwały (słowo mówione)
ma nadawcę i odbiorcę
nadawca wytwarza znak, po to, aby został dostrzeżony przez odbiorcę oraz, po to, by wywołał on u odbiorcy myśl o treści ustalonej przez nadawcę
nadawca i odbiorca znają umowę, czyli konwencję jaką ów znak należy zinterpretować
nic nie staje się znakiem jak tylko wtedy, gdy zostanie on zinterpretowany
Komunikacja - polega na nadawaniu, przetwarzaniu i odbieraniu znaków.
Schemat komunikacji
NADAWCA ODBIORCA
KOMUNIKAT
Język, jego funkcje, perspektywy jego badania.
Język - jest to system umownych znaków słownych
Kompetencja językowa - umiejętność wytwarzania i interpretowania znaków słownych
Cecha języka:
użytkownik języka potrafi produkować i interpretować wiele zdań, nawet tych, których nigdy nie widział
użytkownik języka potrafi wykrywać zdania wieloznaczne i ustalić ich możliwą interpretację
Narzędzia języka:
do przekazywania informacji
do zwrócenia uwagi
do wyrażania i wywoływania stanów wewnętrznych
do powstrzymania działania
Funkcję języka:
funkcja informacyjna - przekazuje informacje
funkcja estetyczna - zwrócenie uwagi na sposób organizacji komunikatu, zasada przezroczystości znaku, w trakcie komunikacji znakowej nie zauważana jest na ogół forma znakowa
funkcja ekspresywna - wyrażanie i wzbudzenie pewnych stanów wewnętrznych, np. uczuć
funkcja persfazyjnosugestywna - na plan pierwszy wysuwa się zakazywanie czegoś lub jakiegoś działania, funkcja ta też przekonuje kogoś do czegoś
funkcja fatyczna - występują wypowiedzi podtrzymania, rozpoczęcia lub zakończenia rozmowy
Język naturalny a sztuczny, język sformalizowany a niesformalizowany, język zinterpretowany a nieinterpretowany, język przedmiotowy a metajęzyk.
JĘZYK NATURALNY
język potoczny i używany przez nas na co dzień, przekaz kulturowy. Słownik tego języka jest zbiorem otwartym |
JĘZYK SZTUCZNY
język zbudowany specjalnie dla określonych celów. Słownik tego języka jest zbiorem zamknięty
|
JĘZYK SFORMALIZOWANY
Język w szczególny sposób opisany, język spełnia określone postulaty efektywności
|
JĘZYK NIESFORMALIZOWANY
|
JĘZYK ZINTERPRETOWANY
język posiadający reguły znaczeniowe, wyrażenia zostały podporządkowane reguły
|
JĘZYK NIEZINTERPRETOWANY
nie wymaga podania reguł znaczeniowych, charakteryzacja poprzez reguły składniowe i słownikowe
|
JĘZYK PRZEDMIOTOWY
|
METAJĘZYK
język służący do opisywania pewnego innego języka (tzw. języka przedmiotowego), zawierający nazwy wyrażeń tego języka, nazwy właściwości tych wyrażeń oraz związków, jakie między nimi zachodzą.
|
Gramatyka kategorialna: pojęcie kategorii gramatycznej, rodzaje kategorii gramatycznych.
Kategoria gramatyczna - α języka „j” nazywamy zbiór tych wszystkich wyrażeń tego języka, którymi możemy bez utraty poprawności gramatycznej zastąpić wyrażenia α w dowolne wyrażenie β języka „j”.
Dwa wyrażenia należą do tej samej kategorii gramatycznej wtw, kiedy są zastępowalne w danym wyrażeniu złożonym bez utraty poprawności gramatycznej tego wyrażenia
Kategorie gramatyczne dzielimy na:
samodzielne (podstawowe) nazwy, zdanie jednostkowe (nazwy):
imiona, nazwy własne, np. Ryry
jednoznaczne, charakterystyczne, np. najwyższy szczyt w Tatrach
niesamodzielne (pochodne) - różnego rodzaju funktory - nie stanowią samodzielnych jednostek
Nazwa, jej desygnat i treść językowa (konotacja). Klasyfikacja nazw.
Nazwa - jest to dowolne wyrażenie, które może wystąpić w roli podmiotu lub orzecznika w zdaniu
podmiotowo - orzecznikowym, czyli w zdaniu o budowie <podmiot> jest <orzecznik> np. Fido jest psem
Desygnat - jest to przedmiot oznaczony przez tą nazwę. Zbiór wszystkich desygnatów danej nazwy tworzy jej zakres. Posiada wiele cech ważnych lub mniej ważnych.
Treść językowa)konotacja) - jest to zbiór cech, które użytkownik języka używając tej nazwy przypisuje wszystkim jej możliwym desygnatem. Pewne cechy przysługują desygnatom w sposób istotny (konstytuowany) lub pochodny (konsekutywny).
Np. Kwadrat
konstytutywne - czworoboczność, prostokątność, równoboczność
konsekutywne - posiadanie równych przekątnych
Podział nazw:
ze względu na budowę:
proste (jeden wyraz)
złożone (kilka wyrazów)
ze względu na liczbę desygnatów:
puste (brak desygnatów)
jednostkowe (dokładnie jeden desygnat)
ogólne (więcej niż jeden desygnat)
ze względu na sposób wskazywania desygnatów:
generalne (nazwa przysługująca przedmiotowi ze względu na cechy jakie są mu przypisywane), np. kwadrat
indywidualne (nazwa przysługująca przedmiotowi ze względu na ustawienia), np. akt chrztu
ze względu na rodzaj desygnatu:
konkretne (desygnat osobowy, rzeczy), np. krasnoludek
abstrakcyjne (nazwy podmiotów abstrakcyjnych - cechy stosunków zdań), np. białość, przyjaźń, cisza
ze względu na strukturę wewnętrzną:
zbiorowe (desygnat jest pewną całością złożoną z części [argumentów], np. las, biblioteka
nie zbiorowe (desygnaty - są przedmiotami prostymi), np. stół
Zdanie: zdanie proste a zdanie złożone, sąd w sensie logicznym a sąd w sensie psychologicznym, zdanie analityczne zdanie kontradyktyczne, zdanie semantyczne.
Zdanie - jest to jednostka komunikacyjna. Oznacza wartości logiczne i oznacza stany lub sytuacje.
Sąd w sensie logicznym - treść zdania- informacje przekazywana przez zdanie o jakimś stanie rzeczy np. Ziemia jest kulista.
Sąd w sensie psychologicznym - sąd utożsamiany z myślą. Myśl związana przez kogoś w związku z jakimś zdaniem.
Zdanie analityczne - zdanie, które jest prawdziwe na mocy swej struktury i znaczenia występujących w nim wyrażeń np. Kwadrat ma cztery boki. Poznań leży nad Wartą lub nie leży nad Wartą.
Zdanie kontradyktyczne - (wewnętrzne spostrzeżenie) zdanie, które jest fałszywe na mocy swej struktury i znaczenia występujących wyrażeń np. Trójkąt ma cztery boki. Poznań leży i nie leży nad Wartą.
Zdanie semantyczne - zdanie, którego stwierdzenie prawdziwości lub fałszywości wymaga kontaktu poznawczego z rzeczywistością np. Poznań leży nad Wartą.
Spójnik ekstensjonalny a spójnik intensjonalny.
Spójnik ekstensjonalny, czyli prawdziwościowe, np. Nieprawda, że A
prawda 0 fałsz
Charakteryzuje się tym ,że wartość logiczna zdania złożonego, utworzonego przy jego pomocy, zależy tylko od wartości logicznych zdań składniowych np. „Jest prawdziwe, że”
„i”
„lub”
„ani…ani”
Spójnik intensjonalny - to taki, że wartość logiczna zdania złożonego utworzonego przy jego pomocy zależy także od treści zdań.
np. możliwe, że A możliwe, że B
0 0
Wiadomo, że
Myślę, że
negacja „~” - polega na poprzedzeniu formuły A, np. ~(A) czytamy: nieprawda, że; nie jest tak; nie. Zdania nazywamy negacjami lub zaprzeczeniem. Gdy formuła A jest prawdziwa to negacja jest fałszywa i gdy formuła jest fałszywa to negacja jest prawdziwa.
koniunkcja ^ - polega na połączeniu dwóch formuł, np. (A)^(B) formuły te nazywamy czynnikami. Symbol ten oznacza: i, oraz, a, ale, lecz, natomiast. Komunikacja jest prawdziwa gdy oba czynniki są prawdziwe, natomiast fałszywa, gdy co najmniej jeden czynnik jest fałszywy.
alternatywa v - połączenie formuły (A)v(B); formuły te nazywamy składnikami. Zdanie nazywamy alternatywą; spójnik to: lub, bądź. Alternatywa jest fałszywa, gdy oba składniki są fałszywe, natomiast jest prawdziwa, gdy co najmniej jeden składnik jest prawdziwy. Używa się go w sensie wykluczającym, gdy składniki maja różne znaczenia logiczne, np. Poślubię albo Adama albo Marka. Jeżeli alternatywa jest prawdziwa, któryś z jej składników jest fałszywy, to drugi składnik musi być prawdziwy.
implikacja -> połączenie formuły (A)->(B) formuła przed znakiem implikacji to poprzednik, a za znakiem implikacji to następnik. Spójnik czytamy: jeżeli.., to; Jeżeli <poprzednik>, to < następnik>; jeśli.., to; o ile… to. Zdania nazywamy warunkami lub okresy warunkowe. Implikacja formuły (A) (B) jest fałszywa, gdy poprzednik jest prawdziwy, a następnik fałszywy.
równoważność ≡ - (A) ≡ (B) czytamy: wtedy i tylko wtedy. Równoważność formuły jest prawdziwa, gdy dwa składniki są prawdziwe. Każde zdanie równoważne prawdziwe jest prawdziwe i odwrotnie
Uzasadnienie i typy racji. Stosunek uzasadniania zdania przez zdanie.
Uznawanie - pojęcie relacyjne zdanie uznane w systemie wiedzy i uznane przez kogoś
(teza tego systemu) (treścią jest przekonanie żywione przez kogoś)
Wiedza w sensie obiektywnym - uznany system wiedzy zdanie uznane przez kogoś - wiedza w sensie subiektywnym
Zdanie odrzucone w systemie wiedzy
Zdanie odrzucone przez kogoś.
Uzasadnienie - to wskazanie racji dla uznania bądź odrzucenia zdania.
Typy racji
nauki empiryczne
nauki formalne
Typy racji uznawania zdań:
racje czerpane z różnego rodzaju spostrzeżeń i doświadczenia zmysłowego i niezmysłowego
racje wskazane poprzez rozumowania i argumentacje
Typy uzasadniania zdań:
uzasadnianie bezpośrednie - polega na odwołaniu się do spostrzeżeń i doświadczeń jako racji uznania lub odrzucenia zdania
uzasadnienie pośrednie - polega na odwołaniu się już do wcześniej uznanych zdań.
<A1…..A1…w>
Przesłanka wniosek
Możemy uzasadnić jakieś zdanie:
wprost poprzez wyprowadzenie go z jakiś zdań wcześniej uznanych za prawdziwe
nie wprost poprzez obalenie jego zaprzeczenia tj. poprzez wykazanie, że z jego zaprzeczenia wynika logicznie jakiś fałsz (np. sprzeczność) metoda nosi nazwę:
reductio ad absurdum lub reductio ad falsum
Przykłady
przez reductio ad absurdum można uzasadnić twierdzenie, że cnoty nie można się nauczyć.
Gdyby cnoty można było się nauczyć, to ludzie dobrzy nauczyliby jej swoich synów, wiadomo, że ich synowie nie są dobrzy.
prze reductio as absurdum można uzasadnić twierdzenie, że niektóre poglądy są prawdziwe, obalając twierdzenie, że
(s) żaden pogląd nie jest prawdziwy
Załóżmy, że pogląd (s) jest prawdziwy. Wtedy zgodnie z tym co głosi ów pogląd - żaden pogląd nie jest prawdziwy. W szczególności więc nie jest prawdziwy pogląd (s)
Wbrew temu, co założyliśmy.
Rozumowanie a argumentacja.
Zarówno rozumowania jak i argumentacje przeprowadzone Sącze względy na pewne zdania, które się uzasadnia. Przy czym w argumentacji dochodzi jeszcze wzgląd na osobę lub osoby, które się przekonuje. Rozumowanie może służyć osiągnięciu następujących celów poznawczych:
wzbogaceniu systemu wiedzy obiektywnej lub subiektywnej poprzez odwołanie się do zdań już należących do tego systemu
może służyć podniesieniu wartości poznawczej danego zdania
ustalenie związków między tym, co już znane ( co wchodzi w skład naszej wiedzy)
W argumentacji chodzi o dokonanie zmiany w obrębie wiedzy subiektywnej. Chodzi o usunięcie wyłącznie włącznie do wiedzy subiektywnej.
Rozumowania oceniamy z punktu widzenia ich poprawności logicznej. Natomiast argumentacje oceniamy jeszcze ze względu na ich skuteczność.
Rozumowania lub argumentacje są poprawne logicznie gdy:
wszystkie użyte przesłanki są prawdziwe
uzasadniona teza wynika logicznie z przesłanek
Argumentacja jest poprawna praktycznie, gdy:
wszystkie użyte przesłanki są akceptowane
uzasadniają wnioski
Argumentacja jest skutera, gdy:
prowadzi do osiągnięcia zamierzonego celu (np. zmiana przekonań) prowadzi do uznania lub odrzucenia przez kogoś zdania będącego przedmiotem argumentacji.
Pojęcie wnioskowania, rodzaje wnioskowań i błędy wnioskowania dedukcyjnego.
Wnioskowanie - to istotna część rozumowania i argumentacji. Proces myślowy (pragmatyczny proces myślowy), w którym na podstawie wcześniejszego uznania pewnych zdań (przesłanek) dochodzi się do uznania kolejnego zdania w ogóle nie używanego, bądź uznanego z mniejszą dozą pewności zwanego wnioskiem lub konkluzją.
Kryterium podziału wnioskowań
rodzaj stosunku uzasadniania
stopień prawdopodobieństwa z jakim uznajemy wniosek z uwagi na stopień prawdopodobieństwa z jakim uznaliśmy przesłanki
WNIOSKOWANIA
niezawodne zawodne logiczne
(dedukcyjne) (uprawdopodobniające) (bezwartościowe)
Wnioskowanie dedukcyjne - to wnioskowanie, w którym wniosek wynika logicznie z przesłanki (tj. zasadą tego wnioskowania jest niezawodna reguła wnioskowania).
Przykład:
jeżeli Zenek był w pracy to spotkał Wacka. Ale Zenek nie spotkał Wacka. A zatem nie był w pracy
każda abra jest kadabrą. Każda Kadara jest Mement. A zatem każda Aare jest Mameną.
Dwa warunki poprawności wnioskowań dedukcyjnych:
oparcie się na regule niezawodnej
właściwe przypisanie przesłankom i konkluzji wartości logicznych lub poznawczych przez wnioskującego
Wnioskujący może popełnić dwa rodzaje błędów:
formalny - wnioskujący konkluzję, która nie wynika logicznie z przesłanek
materialny - wnioskujący przejmuje fałszywą przesłankę.
Błędy jakimi mogą być obciążone wnioskowania
błąd materialny - błąd wnioskowania popełniany, gdy do uzasadnienia wniosku używa się fałszywych przesłanek.
błędne koło (bezpośrednie) - polega na tym, że do uzasadnienia wniosku W wykorzystuje się sam wniosek W lub jakieś zdanie z nim trywialnie równoważne.
Np. Dusza jest nieśmiertelna, gdyż nigdy nie umiera.
Przesłanka jest trywialnie synonimiczna z wnioskiem.
Do uzasadnienia zdania A używa się zdania B i na odwrót
A B![]()
Ludzie są niegodziwi, bo natura ludzka jest zepsuta, a to, że natura ludzka jest zepsuta najlepiej poznać po niegodziwości ludzi.
(jest to częste zjawisko. Im więcej przesłanek tym większe ryzyko, że błędne koło się pojawi)
błąd formalny - powstaje wtedy, gdy wnioskujący jest przekonany, że wnioskuje dedukcyjnie, tym czasem reguła wedle, której przeprowadza wnioskowanie jest zawodna tj. wniosek nie wynika logicznie nawet po uwzględnieniu przesłanek ukrytych.
błąd wnioskowania z prawdziwości następnika implikacji:
![]()
Jeżeli lekarstwo jest skuteczne to chory wyzdrowiał. A ponieważ chory wyzdrowiał, to lekarstwo było skuteczne.
błąd wnioskowania z negacji poprzednika implikacji
![]()
![]()
Jeżeli rozumujesz poprawnie, dochodzisz do poprawnej konkluzji, ponieważ nie rozumujesz poprawnie, więc nie dochodzisz do poprawnej konkluzji.
błędna konwencja
![]()
Jeżeli oskarżony jest winny to był na miejscu zbrodni, stąd jeśli jest niewinny to nie był na miejscu zbrodni (formalnie niepoprawne)
Wnioskowanie uprawdopodabniające - to wnioskowanie, w którym:
prawdziwość przesłanek nie gwarantuje prawdziwości wniosku, czyli nie jest wykluczona fałszywość wniosku mimo prawdziwych przesłanek.
stopień pewności, z jakimi uznaje się wniosek nie jest większy niż prawdopodobieństwo wniosku określone dla danych przesłanek.
Wnioskowanie redukcyjne - to wnioskowanie uprawdopodabniające, w którym przesłanki wynikają za wniosku, zaś wniosek nie wynika logicznie z przesłanek.
Porównanie wniosków
![]()
dedukcyjne: przesłanka = racja logiczna P
wniosek = następstwo logiczne
![]()
redukcyjne: przesłanka = następstwo logiczne
wniosek = racja logiczna W
Przykłady wnioskowań redukcyjnych:
agata jest przesądna. Beata jest przesądna itd. A zatem, każda kobieta jest przesądna
zjawisko Z nie zostało dotąd wytłumaczone. A zatem, zjawisko Z jest niewytłumaczalne
Prawdziwość przesłanek powinna gwarantować większe prawdopodobiństwo wniosku niż jego zaprzeczenie.
Rodzaje rozumowań: dowodzenie, wyjaśnianie, sprawdzenie hipotez.
Rozumowanie - złożone procesy, wnioskowania zamykają rozumowanie.
Czynności rozumowania:
sformułowanie problemu
przegląd dostępnej wiedzy, która może być przydatna przy rozwiązywaniu podjętego problemu i sporządzenie listy założeń, które powinny zapewnić rozstrzygnięcie problemu
wskazanie ścieżki, która z uwagi na przyjęte założenia umożliwia uznanie zdania będące rozwiązaniem problemu.
Podstawowe rozumowania
dowodzenie
wyjaśnienie
sprawdzenie
Dowodzenie - jest to rozumowanie polegające na tym, że dla danego zdania B o nieznanej lub wątpliwej wartości logicznej (demonstrandum) poszukujemy zdań A1…An , o których wiemy, że są prawdziwe i z których wynika logicznie zdanie B
Etapy dowodzenia
poszukiwanie racji logicznych wśród zdań uznanych już za prawdziwe
wykazanie, że dane zdanie wynika logicznie z wyszukanych zdań
Rozwiązanie uzasadniające i dedukcyjne
Wprost: wykaż, że B
wiadomo, że A
wiadomo, że jeśli A to B
na pewno B
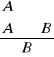
A1….An => B
Wprowadza się prawdę!
Nie wprost
wykaż, że B
przypuśćmy, że nie-B
wiadomo, że jeśli nie-B to C
0 1 0
wiadomo, że nie-C
na pewno B
Wprowadza się jakiś fałsz!
Dowodząc przeszukujemy nowych prawd opierając się o prawdy znane, poszukujemy związku między tym, co już wiemy.
Wyjaśnienie - jest to rozumowanie, w którym dane jest pewne zdanie, które jest uznane i ma być uzasadnione oraz tworzony jest pewien zbiór zdań, które mają uzasadnić. Jest to rozumowanie, które ma na celu dostarczenie odpowiedzi: Dlaczego Z (zdanie uznane) opisujące jakieś zjawisko. Zdanie Z jest to eksplanandum. Odpowiedź to ekspalnanas.
Sprawdzanie hipotezy - jest to rozumienie polegające na tym, że zdania B o nieznanej lub wątpliwej wartości logicznej, które traktujemy jako hipotezę, wyprowadzamy wiele różnorodnych następstw logicznych A1…An, których wartości logiczne możemy sprawdzić np. przez obserwację lub eksperymenty. Hipoteza B ma uzasadnić zdania A1…An i nie jest zdaniem uznanym.
Dwa przypadki sprawdzania:
przynajmniej jedno ze zdań A1….An jest fałszywe wtedy hipoteza b jest fałszywa, dokonujemy falsyfikacji (obalenie hipotezy)
wszystkie zdania A1….An okazują się prawdziwe i nie napotykamy na żadne zdanie fałszywe wynikające logicznie z hipotezy B. Badana hipoteza zostaje uprawdopodobniona - weryfikacja hipotezy
Schemat sprawdzania
Sprawdzanie, czy B
Falsyfikacja: wiadomo, że: Jeżeli B to A1 i An
wiadomo, że: nie - A (dla 1 ≤ 0 ≥ n)
na pewno: nie - B
potwierdzenie: wiadomo, że: Jeżeli B to a1 i An
wiadomo, że A1…An
przypuszczenie: B
Dowodzenie
demonstrandum
Wyjaśnienie
Sprawdzenie
Sprawdzenie
H
?
Język KRZ słownik formuły) Schematy zdań.
Definicja formalna języka KRZ:
każda zmienna zdaniowa jest formułą KRZ
jeżeli A,B są formułami KRZ to wyrażenia:
~(A);(A)^(B);(A)v(B);(A)->(B);(A)≡(B); są formułami KRZ
nie ma innych formuł poza zmiennymi zdaniowymi i takimi formułami, które można zbudować dzięki zastosowaniu reguły 2
Przykłady
Formułami są: p; ~p; ~~p; p ^ q; ~(p -> ~q)
Formułami nie są: p ~q; p -> q; ~p -> q; ~pq
Definicja podformuły - dozwoloną cześć formuły A, która sama jest formułą nazywamy podformułą formuły A. Do podformuły formuły A zaliczamy samo A.
Przykłady
Formułą jest: p -> ~(q ^ ~r)
jej podformułami są:
p; q; r; ~r; q ^ ~r; ~(q ^ ~r)p -> ~(q ^ ~r)
p -> ~(q ^ ~r)
p ~(q ^ ~r)
q ^ ~r
q ~r
^ r
Schematy zdań
Jeśli mówisz nie prawdę ale czynisz to nie świadomie to nie kłamiesz
Niech p - mówisz nieprawdę
q - czynisz to nieświadomie
r - kłamiesz
wówczas: (p^ q) ~ r
Zdam egzamin z logiki lub go nie zdam
Niech p - zdam egzamin z logiki
wówczas: p v ~p
Nie potrafisz kontrolować swoich rozumowań, wtw gdy nie znasz zasad logiki
Niech p - potrafisz kontrolować swoich rozumowań
q - znasz zasady logiki
wówczas: ~p ≡ ~q
Jeżeli wprowadziłeś alternatywę, to o ile jeden jej składnik nie jest fałszywy to wypowiedziałeś zdanie prawdziwe.
Niech p - wprowadziłeś alternatywę
q - jeden jej składnik jest fałszywy
r - wypowiedziałeś zdanie prawdziwe
wówczas: p (~q r)
Jeżeli wygrasz ten proces, to otrzymasz znaczny spadek, a jeśli go przegrasz to będziesz musiał opłacić znaczne koszty sądowe.
Niech p - wygrasz ten proces
q - otrzymasz znaczny spadek
r - go przegrasz
s - będziesz musiał opłacić znaczne koszty sądowe
wówczas: (p q) ^ (r s)
Charakterystyka semantyczna KRZ: funkcja wartościowania, tautologia i kontrtautologia, relacje wynikania semantycznego, pojęcie nie zawodnej reguły wnioskowania. Wybrane tautologie.
Wartościowanie - wartościowaniem formuł w KRZ nazywamy dowolną funkcję V ze zbioru formuł KRZ w zbiór wartości logicznych (0,1) taką, że dla dowolnych formuł A i B zachodzi:
Jeżeli v(A) v(B) to v(~A) v(A v B) v(A ^ B) v(A -> B) v(A ≡ B)
v(A) |
v(B) |
to |
v(~A) |
v(A v B) |
v(A ^ B) |
v(A B) |
v(A ≡ B) |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
v(A) wartość logiczna formuły A
Wnioski!
wartość formuły jest jednoznacznie zdeterminowana wartościami jej podformuły
znając wartość podformuły można wyliczyć wartość całej formuły
z punktu widzenia wartościowania formuł wyróżniamy 3 rodzaje:
formuły, które dla każdego wartościowania przyjmują wartość 1- tautologie (schematy zdań wyłącznie prawdziwych)
formuły,które dla każdego wartościowania przyjmuje wartość 0 - kontr tautologie (schematy zdań wyłącznie fałszywych)
formuły, które dla pewnych wartościowań przyjmują wartość 0 lub 1 (dla innych)
Tautologia i kontrtautologia
formuła A jest tautologia klasycznego rachunku zdań i tylko wtedy, gdy dla każdego wartościowania v v(A)=1
formuła A jest kontr tautologią klasycznego rachunku zdań kiedy, tylko wtedy, gdy dla każdego wartościowania v v(A)=B
Wynikanie semantyczne - z formuł A1….An wynika semantycznie na gruncie KRZ formuła B wtw, gdy implikacja (A1 ^…..^ An) -> B
Jest tautologią KRZ
Przykład 1
jeśli wnioskujesz dedukcyjnie to wniosek wynika logicznie z przesłanek.
wniosek nie wynika logicznie z przesłanek, wynika semantycznie (logicznie) zdanie.
nie wnioskujesz dedukcyjnie
[(p -> q) ^ ~q] -> ~p
Jest tak bo implikacja a ^ b -> c podpada pod prawo modus tollendo tollens
[(p -> q)^~q] -> ~p
Wnioskowanie - jakakolwiek skończona co najmniej dwuelementowa sekwencja zdań, z których ostatnie jest wnioskiem a wszystkie zdania poprzedzające wniosek to przesłanki.
Wnioskowanie logiczne (poprawne lub dedukcyjne) - jest wtedy, gdy schematem jest pewna niezawodna reguła, która prowadzi od prawdziwych przesłanek do prawdziwych wniosków.
schematy przesłanek
![]()
Schemat wniosku
są to formuły języka KRZ
Substancja S jest kwasem lub zasadą. Jeżeli S jest kwasem to barwi papierki lakmusowe na czerwono. Ale S nie barwi papierka na czerwono - przesłanki
Zatem S jest zasadą,
Schemat 1
p=1![]()
} p v q ![]()
r=1 } 1 p -> r
r=0 }
sprzeczność 0 ![]()
Pozostaje sprawdzić czy reguła jest niezawodna.
Reguła wnioskowania - (schematem wnioskowania, wyrażaną w języku KRZ) nazywamy dowolny skończony, co najmniej dwu wyrazowy ciąg formuł języka KRZ. Ostatnią formułę nazywamy schematem wniosku, a formułę wcześniejszą schematem przesłanek.
Przykłady:
p, q / p ^ q
p≡ ~q, p ≡ q / (p ≡ ~q) ^ (~p ≡ q)
p -> ~~q, q / ~p
reguła niezawodna - reguła A1….An / B jest niezawodna wtw, gdy implikacja (A1^…^An ) -> B jest tautologia KRZ wtw, gdy z formuł A1….An wynika semantycznie formuła An w pierwszym przypadku reguła jest zawodna.
Twierdzenie
Jeżęli reguła A1…An / B jest niezwodna, a formuła A1…An uzyskuje wartość 1 to formuła B też uzyskuje wartość 1.
Zakładamy, że: ![]()
jest niezawodna
i że
r(A1) = 1,…,r(An) =1
r(B) = 0
r((A1 ^…..^ An) -> B) = 0
(A1 ^….^ An) -> nie jest tautologią.
Przykłady reguł niezawodnych
Reguła oparta na prawie modus Ponendo ponens
![]()
Prawo modus tollendo
![]()
Sylogizm hipotetyczny
![]()
![]()
(p -> q) -> (~q -> ~p)
Prawo redukcji do absurdu
![]()
Każda tautologia jest zadaniem prawdziwym, ale nie każde zadnia prawdziwe jest
A -> B
1 -> ?
Tautologie dotyczące zdań sprzecznych
PRAWO WYŁĄCZNEGO ŚRODKA
p v ~p
PRAWO NIESPRZECZNOŚCI
~(p ^ ~q)
NIERÓWNOWAŻNOŚCI SPRZECZNOŚCI
~(p ≡ ~p)
DUNSA SZKOTA
(p ^ p) -> q
Tautologie dotyczące zaprzeczenia
SILNE PRAWO PODWÓJNEJ NEGACJI
~p ≡ p
PRAWO NEGOWANIA KONIUNKCJI
~(p ^ q) ≡ (~p v q)
PRAWO NEGOWANIA ALTERNATYWY
~(p ^ q) ≡ (~p ^ ~q)
PRAWO NEGOWANIA RÓWNOWAŻNOŚCI
~(p ≡ q) ≡ [(p ^ ~q) v (q ^ ~p)]
PRAWO NEGOWANIA IMPLIKACJI
~(p -> q) ≡(p ^ ~q)
Tautologie dotyczące implikacji
PRAWO SYLOGIZMU HIPOTETYCZNEGO
(p -> q) -> [(q -> r) -> (p -> r)]
MODUS PONENDO PONENS (sposób na potwierdzenie przez potwierdzenie)
[(p -> q) ^ p] ->q
MODUS TOLLENDO TOLLENS (sposób na odrzucenie przez odrzucenie)
[(p -> q) ^ ~q] -> ~p
PRAWO REDUKCJIDO ABSURDU
[(p -> q) ^ (p -> ~q)] -> ~p
Tautologie dotyczące równoważności
PRAWOROZKŁADANIA RÓWNOWAŻNOŚCI
(p ≡ q) ≡ [(p -> q) ^ (q -> p)]
PRAWO OBUSTRONNEGO NEGOCJOWANIA RÓWNOWAŻNOŚCI
(p ≡ q) ≡ (~p ≡ ~q)
Metoda 0 -1
ŻEBY FORMUŁA BYŁA TAUTOLOGIĄ WARTOŚCI FORMUŁY (OSTATNIA KOLUMNA) MUSI MIEĆ WARTOŚĆ 1!
[(p q) ^ ~q] p
p |
q |
~q |
p q |
(p q) ^ ~q |
[(p q) ^ ~q] p |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Formuła nie jest tautologią ponieważ pojawiło się 0
[(p q) ^ ~q] ~p
p |
q |
~p |
~q |
p q |
(p q) ^ ~q |
[(p q) ^ ~q] ~p |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Formuła jest tautologią
I II
[(p ≡ q) ~r] [ ~p ^ ~(q v r)]*
p |
q |
r |
~p |
~r |
p≡q |
I |
q v r |
~(q v r) |
II |
* |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Formuła nie jest tautologią
[(p q) ^ ~p] ~q q= 1
1 0 0 p=0
poprzednik następnik
1 1 1
0 -> 1 0
Formuła nie jest tautologią
[(p q) ^ ~q] ~p założenie p=1
1 0 0 fałszywe q=0
1 1 1
0
1 0
0 Formuła jest tautologią
(p ≡ q) [(p ~r) v ~(q ^ r)]
0 p=1
1 0 00 1 q=1
1 0 1 1 r=1
1
1≡1
1 Formuła jest tautologią
[(p ^ ~q) r] ≡ [ ~(p v r) q]
0 0 p=0
1 1 0 q=0
0 r=0
0 0
(0 ^ ~0) 0
0 0
1 Formuła nie jest tautologią
KRZ jako system aksjomatyczny oraz jako system dedukcji naturalnej.
Charakterystyka syntaktyczna KRZ
Systemy syntaktyczne rachunku zdań buduje się dowody używając reguły dedukcyjne.
Systemy aksjomatyczne Systemy dedukcji naturalnej
(bada obiekty za pomocą odpowiednich pojęć:
- pojęcia specyficzne, spójniki zdaniowe
- twierdzenia pierwotne, aksjomaty)
Aksjomat - to tyle, co twierdzenie, którego w ramach pewnej teorii się nie dowodzi nie muszą być prawdami oczywistymi. Aksjomatami są wybrane tautologie. Z aksjomatów wyprowadza się twierdzenia pochodne (za pomocą reguł wnioskowania)
Systemy dedukcji naturalnej - różnią się od aksjomatów tym, że w dowodzeniu twierdzeń nie używa się aksjomatów, a środkami dowodzenia są reguły informacyjne ( reguły operowania różnymi spójnikami)
Twierdzenie
A1 [A2 -> [ … (an -> B)…]]
Prawo sylogizmu hipotetycznego
(p -> q) -> [(q -> r) -> (p -> r)]
A1 -> [A2 -> (A3 -> B)]
G. Genten, St. Jasiński - zbudowali systemy dedukcji naturalnej
System oparty na regułach
Reguły dołączania (wprowadzania) |
Reguły opuszczania |
A, B / A ^ B
A / A v B B / B v A
A -> B, B -> / A ≡ B
A - A / ┴
|
A ^ B / A A ^ B / B
A v B - A / B
A -> B, A / B
A ≡ B / A -> B A ≡ B / B -> A
|
┴ - dowolny fałsz logiczny (tautologia)
Pojęcie języka pierwszego rzędu. Język KRP (słownik, formuła, zasięg kwantyfikatora, zmienna wolna i zmienna związana). Schematy zdań.
Klasyczny rachunek predykatów
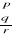
P1 Każdy jest śmiertelnyP2 Sokrates jest człowiekiem
W Sokrates jest śmiertelny
Zdanie proste to zdanie przypisujące pewną własność
Przykład
Ewa kusi Adama. R(a,b)
a R b
Predykat - wyrażenie, które wyraz z jedną bądź wieloma wyrazami tworzy zdanie.
Ewa kusi naiwnego Adama R(a, φ(b))
nazwa złożona = funktor
φ(b)
naiwny - φ
w klasycznym rachunku predykatów występują zmienne nazwowe (indywidułowe) = x, y, z, r, x1…
Można wyróżnić schematy zdaniowe, np.
x kocha y, uwodzi zaś z, żyje natomiast z r.
lub
x + y = z
Wszyscy są leniwi (predykat)
L(x): x jest leniwy
![]()
kwantyfikator generalny (ogólny, duży)
lub
![]()
czytamy: dla każdego
dla dowolnego
dla wszystkich
Rola: wiązanie zmiennych ![]()
Zdanie ogólno twierdzące
![]()
: dla każdego x, x jest leniwy.
Niektórzy są leniwi.
![]()
lub kwantyfikator egzystencjalny (szczegółowy, mały)
![]()
czytamy: istnieje takie…, że…
dla, pewnego
niektóre
dla przynajmniej jednego
Rola: wiązanie zmiennych ![]()
Zdanie szczegółowo twierdzące
![]()
: istnieje takie x, że x jest leniwy.
Nikt nie jest leniwy
![]()
zdanie ogólno przeczące
niektórzy nie są leniwi.
![]()
zdanie szczegółowo przeczące
Każda kobieta jest gadatliwa
K(x): x jest kobietą
G(x): x jest gadatliwa
K(x) -> G(x): jeżeli x jest kobietą, to x jest gadatliwa.
![]()
: dla każdego x, jeżeli x jest kobietą, to x jest gadatliwa.
Zdanie ogólno twierdzące
Niektóre kobiety są gadatliwe
![]()
Zdanie szczegółowo twierdzące
Żadna kobieta nie jest gadatliwa.
![]()
Zdanie ogólno przeczące
Niektóre kobiety nie są gadatliwe
![]()
Zdanie szczegółowo przeczące
Tylko kobiety są gadatliwe
![]()
Predykaty dwuargumentowe.
Wszystko jest przyczyną wszystkiego
R9x, y): x jest przyczyną y
![]()
Bóg jest przyczyną wszystkiego
![]()
Istnieje coś, co jest przyczyną wszystkiego
![]()
Wszystko ma swoją przyczynę
![]()
Nic nie jest przyczyną niczego
![]()
Język „J” nazywamy językiem pierwszego rzędu jeśli spełnia on następujące dwa warunki:
słownik jego zawiera:
nieskończenie wiele zmiennych indywidualnych, którymi są pewne litery reprezentujące przedmioty indywidualne z jakiegoś określonego zbioru i odpowiadającego nazwom jednostkowym owych przedmiotów
przynajmniej jeden symbol relacyjny jest predykatem
skończona liczbę spójników
kwantyfikatory wiążące wyłącznie zmienne indywidułowe
znaki techniczne tj. nawiasy (stałe nazwowe mogą ale nie muszą występować)
Symboli należących do słownika języka „J” zgodnie z przyjętymi regułami gramatycznymi budujemy formuły, są nimi te ciągi wyrażeń ze słownika języka „J”, które są schematami poprawnie zbudowanych zdań jakiegoś języka etnicznego.
Język klasycznego rachunku predykatów (KRP) wchodzą następujące grupy symboli
zmienne indywidułowe (nazwowe) x1…xn…
stałe indywidułwe a1…a2…
symbole relacyjne (predykaty) P1…P2…
spójniki zdaniowe ~^v -> ≡
kwantyfikatory
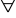
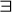
znaki techniczne < > ( )
Argument:
N -> N
Argument (k) liczba argumentów predykatu Pk
P1 Q1 R1 S1
P Q R S
x 1 y1 z1
x y z
a1 b1 c1
a b c
Wyrażenie - każdy skończony ciąg symboli ze słownika języka KRP nazywamy wyrażeniem tego języka.
Atomowa formuła zdaniowa - formułą atomową języka KRP nazywamy dowolne wyrażenie postaci Pk(t1…t2)
gdzie Pk - n-argumentowym predykatem (n=Arg(k)), zaś t1...t2 - są dowolnymi termy
Formę języka KRP nazywamy dowolną zmianę lub stałą indywiduuową.
Formuła atomowa
wszystkie formuły atomowe są formułami języka KRP
jeżeli A, B są dowolnymi formułami języka KRP to wyrażenia postaci:
~(A) (A)^(B) (A)v(B) (A) -> (B) (A) ≡(B) ![]()
(A) ![]()
(A)
nie ma innych formuł języka KRP poza wymienionymi w punktach 1 i 2
formułami są:
![]()
formułami nie są:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zasięg kwantyfikatora - formułą A w formule
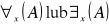
nazywamy zasięgiem odpowiedzialnego kwantyfikatora.
![]()
Zasięg ![]()
Zasięg ![]()
![]()
Zasięg ![]()
Zasięg ![]()
Zmienna związana i wolna. Dany egzemplarz zmiennej x występującej w formule A jest w niej związany, gdy albo występuje on w tej formule bezpośrednio po kwantyfikatorze, albo znajduje się w zasięgu kwantyfikatora wiążącego zmienną x, w przeciwnym przypadku egzemplarz zmiennej x jest wolny w tej formule.
![]()
zasięg ![]()
zasięg ![]()
zmienna
wolna
zmienna
związana
zmienna
związana
zmienna zmienna
związana związana
zmienna
wolna
zmienna
związana Formuły bez zmiennych wolnych
zmienna nazywamy zdaniami.
związana
Pojęcie tautologii KRP i wynikania semantycznego. Wybrane tautologie.
Tautologia KRP (formuła log. prawdziwa) nazywamy, formułą języka klasycznego rachunku predykatów, która jest prawdziwa przy dowolnym rozumieniu występujących w niej symboli relacyjnych (predykatów), stałych indywidualnych (nazw) i zmiennych indywidualnych.
Tautologiami nazywamy schematy zdań wyłącznie prawdziwych. Przykładami tautologii są wszystkie przykłady, które powstają z tautologii KRP zastępując je innymi przykładami z KRZ
![]()
Tautologie KRP
Np. jeżeli wszyscy są leniwi to Zenek jest leniwy.
![]()
dictum de omni (przepowiedziane ze wszystkiego)
Np. Jeśli Zenek jest leniwy to istnieje ktoś, kto jest leniwy
![]()
dictum de singulo (przepowiadanie z pojedynczego)
Np. Jeżeli wszyscy są leniwi, to istnieje ktoś, kto jest leniwy.
![]()
np. jeżeli wszyscy są leniwi to istnieje ktoś, kto jest leniwy.
Prawa de Morgana
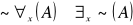
negowania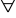
Np. nie wszyscy są altruistami wtw, gdy istnieje ktoś, kto nie jest altruistą
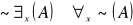
negowania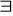
Np. nie istnieją altruiści wtw, gdy nikt nie jest altruistą
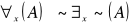
zastępowania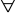
Np. wszyscy są altruistami wtw, gdy nie istnieje ktoś, kto nie jest altruistą
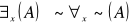
zastępowania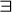
Np. Istnieje ktoś kto jest altruistą wtw gdy nie prawda że nikt nie jest altruistą.
Prawa dotyczące przestawiania kwantyfikatorów
Np. wszystko jest przyczyną wszystkiego wtw, gdy wszystko ma swoją przyczynę we wszystkim
Np. istnieje ktos, kto ma przyjaciela. Istnieje ktoś, kto jest czyimś przyjacielem

prawo przestawiania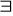
z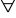
Np. jeżeli istnieje ktoś, kto zdobył każdy ośmiotysięcznik, to istnieje każdy ośmiotysięcznik, który został zdobyty przez kogoś.
Prawa rozdzielności
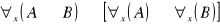
prawo rozkładania dużego kwantyfikatora względem implikacji Np. każdy adwokat jest prawnikiem, to każdy prawnik jest adwokatem
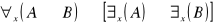
prawo rozkładania małego kwantyfikatora względem implikacji
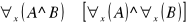
prawo rozkładania dużego kwantyfikatora względem koniunkcji Np. Każdy człowiek jest ssakiem i kręgowcem, każdy jest ssakiem i kręgowcem
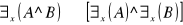
prawo rozkładania małego kwantyfikatora względem koniunkcji
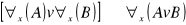
prawo rozkładania dużego kwantyfikatora względem alternatywy Np. każdy polityk kłamie lub każdy polityk jest godzien szacunku, wszyscy kłamią lub wymagają szacunku
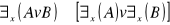
prawo rozkładania małego kwantyfikatora względem alternatywy Np. istnieje coś, co jest kwadratowe lub istnieje coś, co jest okrągłe. Istnieje coś, co jest kwadratowe lub okrągłe.
Klasyczny rachunek predykatu jest teorią nierozstrzygalną choć niektóre jego elementy są rozstrzygalne. Udowodnił to A.Church. Można zaksjomatować KRP i udowodnić, że da się z niego wyprowadzić tautologię. Metoda aksjomatyczna jest tylko metodą połowiczną. Metodą kontrprzykładu jest to przypuszczenie intuicyjne, polega na pokazaniu, że formuła jest schematem zdania fałszywego.
![]()
0
Nie jest to tautologia KRP
![]()
0
![]()
0
![]()
![]()
1 0
![]()
0
nie jest to tautologia
Ze zdań o schematach A1…An wynika semantycznie (logicznie) na gruncie KRP zdanie o schemacie B wtw, gdy formuła o postaci (A1^…^An) -> B jest tautologią KRP
Reguła ![]()
jest niezawodna na gruncie KRP wtw, gdy formuła 0 (a1^…^An) -> B jest tautologią KRZ.
Logika konwersacji. Konwersacja racjonalna i reguły Grice`a.
Odbiorca Znak Nadawca
Komunikat
Konwersja - wymiana zdań:
debata naukowa
dyskusja
P. Grice - teoria konwersacji
Rodzaj ludzkiej współpracy, o której przebiegu decyduje racjonalność posunięć.
Konwersja jest kooperatywna
jeśli cele rozmówców są zgodne (wspólne)
kryteria, za pomocą których oceniamy
Konwencja jest nie kooperatywna
rozmówcy dążą do innych celów
niektóre ważne rzeczy są ukryte
Zasada współpracy (koordynacji)
Każdy uczestnik powinien wnosić do konwersacji taki wkład, jaki na danym jej etapie wymagany z punktu widzenia celów wymiany zdań.
Maksymy Grice (mają wymiar praktyczny i nie są prawami i nie wymagają respektowania, są powinnościami)
reguła jakości
reguła ilości
reguła istotności (relewancji) składa się na zasadę wspópracyreguła sposobu
Reguła jakości
Każdy uczestnik konwersacji powinien wygłaszać poglądy, w których prawdziwość wierzy, i które potrafi uzasadnić.
(Mów zawsze w dobrej wierze)!
Reguła ta zakazuje celowego wprowadzanie w błąd uczestników i zakazuje stwarzania takich sytuacji, które mogą w błąd wprowadzić
Reguła ilości
Uczestnicy konwersacji nie powinni udzielać ani mniej inf. niż jest to konieczne na danym etapie wymiany zdań ani więcej.
(Dostarczaj tyle inf. ile trzeba)!
Reguła zakazuje ukrywania przed rozmówcą inf. jak i zakazuje dostarczania zbyt wielu inf. lub dostarczania inf. nieistotnych dla rozmówcy.
Reguła istotności
Uczestnicy konwersacji nie powinni wygłaszać poglądów, nie związanych treściowo z tematyką konwersacji
(Mów na temat)!
Reguła zakazuje dokonywania zwrotów konwersacji i zakazuje kierowania konwersacji na inną stronę tematu.
Reguła sposobu
Sposób w jaki uczestnicy konwersacji formułują swe wypowiedzi powinien być maksymalnie komunikatywny zwięzły, pozbawiony niejasności i wieloznaczności
(Mów zrozumiale)!
Eksploatacja reguł konwersacji
uczestnik konwersacji może w sposób nie ostentacyjny nie respektować tych reguł.
Może odmówić respektowania tych reguł i zasad
Może znaleźć się w sytuacji konfliktu (spełniając jedną regułę nie spełni innej)
Może naruszyć regułę nie zrywając zasady kooperacji
wytwarza znak
stara się pojąć znak
przekazuje
A |
B |
(A)->(B) |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
A |
B |
(A)v(B) |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
A |
B |
(A)^(B) |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
A |
~(A) |
1 |
0 |
0 |
1 |
A |
B |
(A) ≡ (B) |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
wiedza
E- nans
Wiedza
E-nadum
?
? ?
? ?
?
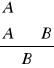
![]()
Wyszukiwarka
Podobne podstrony:
TEORIA FUNKCJONALNO-STRUKTURALNA, praca socjalna studia
Polityka społeczna i zdrowotnaI, Praca socjalna-studia, Polityka społeczna i zdrowotna
Logika sciaga 222, praca socjalna studia
wstep semiotyka argumentacja sciaga-czcionka 5, praca socjalna studia
KOLOKWIUM Z PEDAGOGIKI RESOCJALIZACYJNEJ(2), Praca socjalna, studia - pr soc, resocjalizacja
KRZ-5, praca socjalna studia
Bauman - Emancypacja - Płynna nowoczesność - opracowanie(1), Praca socjalna, studia - pr soc, soc w
Polityka społeczna WIII, Praca socjalna-studia, Polityka społeczna i zdrowotna
Bauman - Globalizacja - opracowanie(1), Praca socjalna, studia - pr soc, ped społeczna
LOGIKA (2), praca socjalna studia
ETYKA W ZAWODZIE NAUCZYCIELA, Praca socjalna, studia - pr soc, etyka
Praca socjalna studia równoległe uniwersytet warszawski
ETYKA!!!, Praca socjalna, studia - pr soc, etyka
Polityka społeczna W5, Praca socjalna-studia, Polityka społeczna i zdrowotna
Polityka społeczna i zdrowotna WII, Praca socjalna-studia, Polityka społeczna i zdrowotna
Platon Uczta, Praca socjalna, studia - pr soc, filozofia
więcej podobnych podstron