Akademia Górniczo-Hutnicza

Wydział Inżynierii Mechanicznej i Robotyki

Wytrzymałość materiałów.

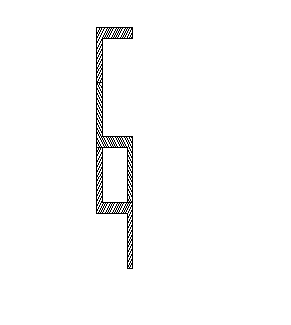
Projekt nr 8

Temat:

Dla podanego przekroju obliczyć główne centralne

momenty bezwładności.

Wykonał:

1. Dane do obliczeń.

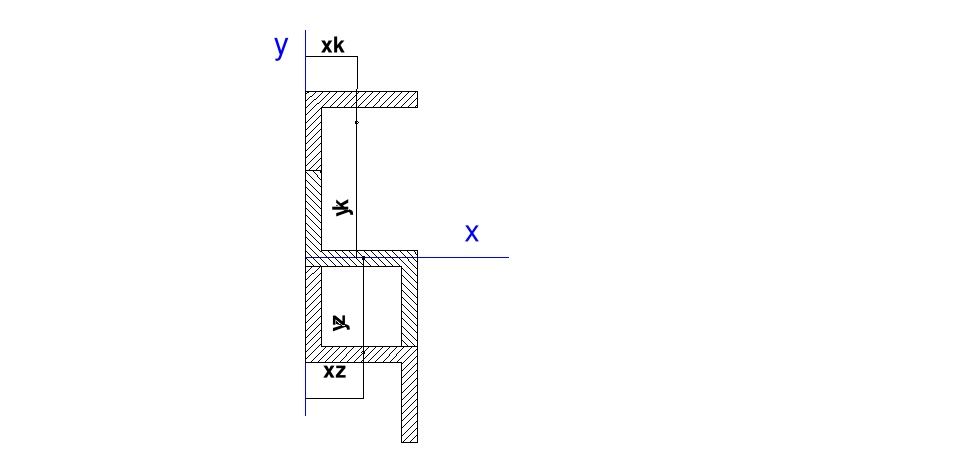
1. Charakterystyka geometryczna kątownika niesymetrycznego L 60x50x5

wg. PN-73/H-93460.05, rys nr 1

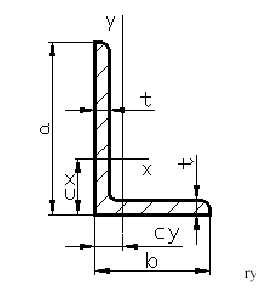
symbol	wielkość
a	60mm
b	50mm
tk	5mm
Ak	4,98cm^2
Ixk	17,94cm^4
Iyk	11,48cm^4
cx	1,91cm
cy	1,39cm
tg	0,713

rys nr 1

2. Charakterystyka geometryczna zetownika Z60 wg PN-65/H-93405

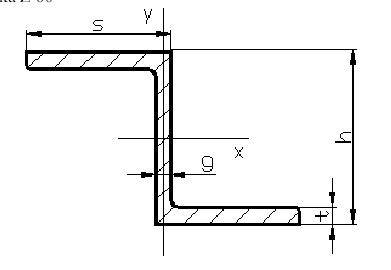
symbol	wielkość
h	60mm
s	50mm
g	5mm
tz	6mm
A	8,5cm^2
Ixz	48,53cm^4
Iyz	43,04cm^4

rys. 1.2

2. Obliczanie środka ciężkości profili względem przyjętych osi x y

2.1. Został przyjęty układ współrzędnych XY gdzie oś X przechodzi przez środek ciężkości pierwszego zetownika. Rys 2.1

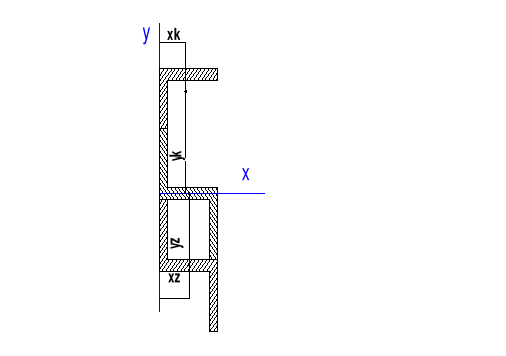
Rys. 2.1

2.2. Obliczanie odległości środków ciężkości poszczególnych pofili od osi XY

profil	kątownik			zetownik 1			zetownik2
sumbol	xk	yk	Ak	xz1	yz1	Az1	xz2	yz2	Az2
wzór	cx	b+s-0,5tz-cy		0,5h			0,5h	-s
wartość	1,91cm	8,31cm	4,98cm^2	3cm	0	8,5cm^2	3cm	-5cm	8,5cm^2

2.3. Obliczanie środka ciężkości całego przekroju wzklędem układu X Y

x_c=
=
=

= -0,05cm

y_c =
=
=

=
= 2,75cm

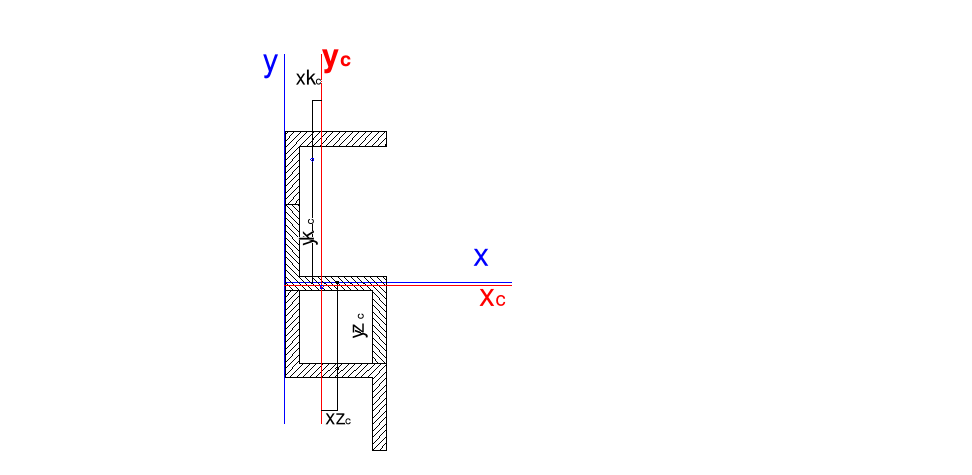
3. Obliczane centralnych momentów bezwładności i dewiacji. Rys 3.1.

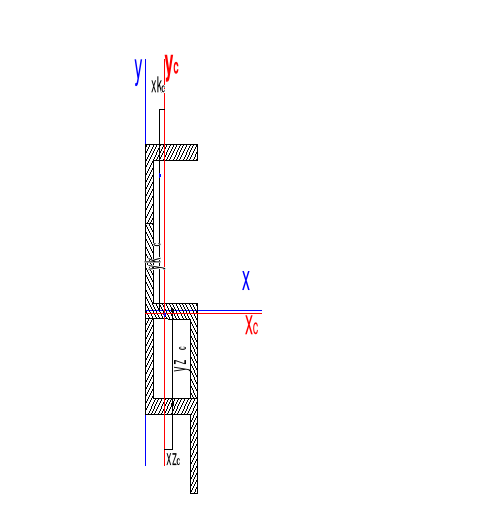
Rys 3.1.

3.1. Obliczanie odległości środków ciężkości profili walcowanych od osi Xc i Yc.

profil	kątownik		zetownik1		zetownik2
symbol	xkc	ykc	xz1c	yz1c	xz2c	yz2c
wzór	xk-yc	yk+xc	xz1-yc	yz1-xc	xz2-yc	yz2-xc
wartość	-0,84cm	8,36cm	0,25cm	0,05cm	0,25cm	-4,95cm

3.2. Obliczanie centralnych momentów bezwładności względem osi Xc, Yc dla całego przekroju z wykorzystaniem wzorów Steinera.

Ixc = Ixc(A_k) + Ixc(A_z1) + Ixc(A_z2) = (Ix_k + A_k*yk_c²) + (Ix_z1 + A_z1*yz1²) + (Ix_z2 +A_z2*yz2²)= = {17,94cm⁴ + 4,98cm² _* (8,36cm)²} + {48,53cm⁴ + 8,5cm²_*(0,05cm)²} + { {48,53cm⁴ + 8,5cm²_*(-4,95cm)²} = 671,34cm⁴

Iyc = Iyc(A_k) + Iyc(A_z1) + Iyc(A_z2) = (Iy_k + A_k*xk_c²) + (Iy_z1 + A_z1*xz1²) + (Iy_z2 + A_z2*xz2²)= = {11,48cm⁴ + 4,98cm²_*(-0,86cm)²} + {43,04cm⁴ + 8,5cm²_*(0,25cm)²} + {43,04cm⁴ + 8,5cm²_*(0,25cm)²} = 102,30cm⁴

3.3.1. Obliczanie momentów dewiacji własnej kątownika względem osi przechodzących przez jego środek ciężkości obliczone po podzieleniu go na dwa prostokąty.

Dxy_k =Dxy(A₁)+Dxy(A₂)= [0+(a_*t_k)_*(-cy+
)_*(
-cx)]+[0+[(b-t)_*t]_*(
-cy)_*(-cx+
)]=

[(6cm_*0,5cm)_*(-1,39cm+0,25cm)_*(3cm-1,91cm)]+[[(5cm-0,5cm)_*0,5cm]_*(2,5cm-1,39cm)_*

_*(-1,91cm+0,25cm)] = -7,8736cm⁴

3.3.2. Obliczanie momentów dewiacji własnej zetownika Z₁ =Z₂ względem osi

przechodzących przez jego środek ciężkości obliczone po podzieleniu go na trzy prostokąty.

Dxy_z = Dxy(A₁)+Dxy(A₂)+Dxy(A₃) = [0+(s_*t_z)_*(-
)_*(
)] + 0 +[0+(s_*t_z)_*

(
)_*(-
)] = [(5cm_*0,6cm)_*(-5cm+0,25cm)_*(3cm-0,3cm)] +

[(5cm_*0,6cm)_*(5cm-0,25cm)_*(-3cm+0,3cm)] = -76,95cm⁴

3.4. Obliczanie momentu dewiacji względem osi Xc, Yc dla całego przekroju z wykorzystaniem wzorów Steinera.

D_xy = D_xy(A_k) + D_xy(A_Z1) + D_xy(A_Z2) = (Dxy_k + A_k*xk_c*yk_c) + (Dxy_Z1 + A_Z1* x _Z1c*y_Z1c) + + (Dxy_Z2 + A_Z2*x_Z2*y_Z2) = [(-7,8736cm⁴)+[(4,98cm²_*(-0,84cm)_*8,36cm]] +

[(-76,95cm⁴) + (8,5cm²_*0,25cm_*0,05cm)] + [(-76,95cm⁴) + [8,5cm²_*0,25cm_*(-4,95cm)]] =

-207,1578cm⁴

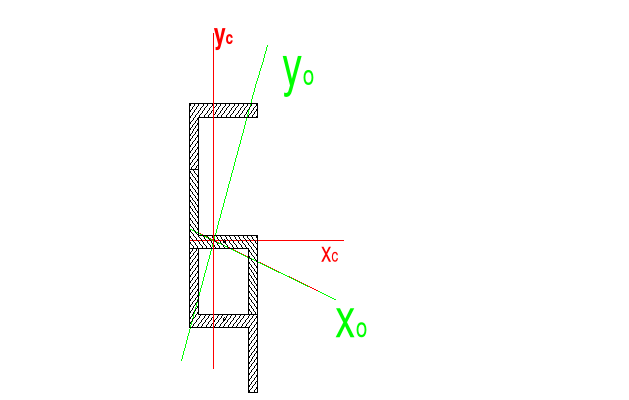
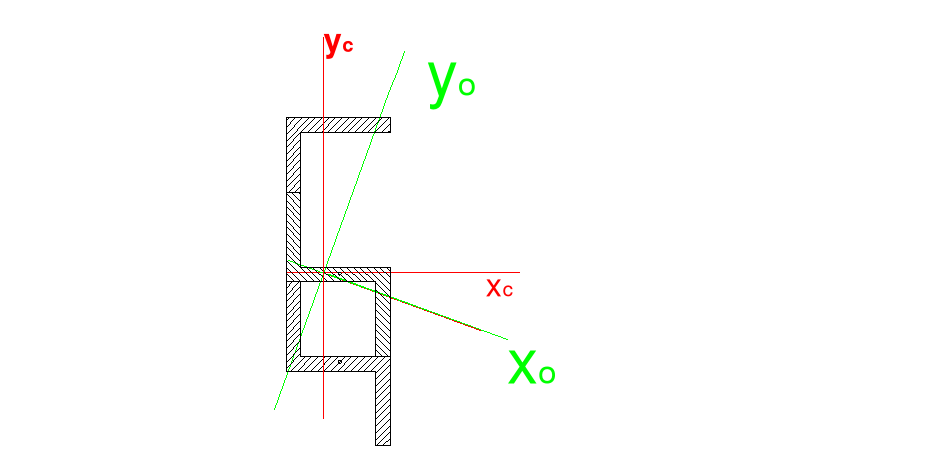
3.5. Obliczanie kąta określającego położenie osi głównych centralnych.

tg 2 =
=
= -0,728

 = -18^o

Literatura.

Siemieniec A, Wolny S.: Wytrzymałość Materiałów. t I. Wydawnictwo AGH, Kraków 2002

---