LABORATORIUM FIZYKI 2 Burzyński Mariusz grR31
Cw14 temat: Własności elektryczne dielektryków.
1 . Podstawy fizyczne.
Jeśli dielektryk zostanie umieszczony w zewnętrznym polu elektrycznym, to znajdujące się w nim ładunki elektryczne (związane i swobodne) ulegną pewnym przesunięciom, a na zewnętrznych powierzchniach pojawią się ładunki polaryzacyjne. Zjawisko to nazywamy polaryzacją dielektryczną. Do jego opisu definiuje się wielkość wektorową P jako elektryczny moment dipolowy jednostki objętości dielektryka lub jako gęstość powierzchniową ładunków polaryzacyjnych na powierzchni prostopadłej do kierunku wektora pola elektrycznego.
Można przyjąć, że w dielektryku umieszczonym w słabym polu elektrycznym E0 polaryzacja P jest proporcjonalna do natężenia pola: ![]()
( gdzie k - podatność elektryczna ). Molekułę traktuje się jako zespół dwóch różnoimiennych ładunków ( jako całość obojętny). Spolaryzowana molekuła jest dipolem elektrycznym - określa ją moment dipolowy: ![]()
(gdzie: q - wartość bezwzględna ładunku, d -odległość między środkami ciężkości ładunków różnoimiennych skierowana umownie od ładunku ujemnego do dodatniego).
Polaryzacja może polegać na:
1) przesunięciu w molekule elektronów względem ich jąder ( tzw. indukowana polaryzacja elektronowa PE
2) doprowadzeniu do jonizacji atomów pod wpływem pola - indukowana polaryzacja jonowa PJ
3) ustawieniu dipoli wzdłuż linii sił pola zewnętrznego - polaryzacja orientacji PO
4) utworzeniu ładunków objętościowych z ładunków swobodnych - polaryzacja objętościowa PS.
Ponieważ powyżej opisane mechanizmy polaryzacji są niezależne, wypadkowa polaryzacja dielektryka wynosi: ![]()
.
Polaryzacja to moment dipolowy jednostki objętości, więc ![]()
(gdzie: N - liczba molekuł w jednostce objętości, ![]()
- średni moment dipolowy cząsteczki). Zakładamy, że ![]()
' (średni moment dipolowy jest proporcjonalny do lokalnego natężenia pola E' działającego na molekułę, -polaryzowalność ).
Paraelektryk jest to taki dielektryk, który posiada wszystki rodzaje polaryzacji oprócz spontanicznej ; ferroelektryk posiada jeszcze polaryzację spontaniczną. Powyżej temperatury TC zwanej temperaturą Curie ferroelektryk staje się paraelektrykiem.
Ferroelektryki posiadają niżej wymienione cechy:a) polaryzacja zależy od temperatury - rośnie, osiąga maksimum, a następnie maleje,
b) polaryzacja silnie zależy od ![]()
- przyłożenie zewnętrznego pola powoduje reorientację polaryzacji w domenach; wraz ze wzrostem ![]()
zaczynają przeważać domeny o kierunku dipoli zgodnym z liniami sił pola, a zanikają domeny, które są ustawione niezgodnie z nimi; w stanie nasycenia w całej objętości kryształu jest tylko jedna domena, w której wszystkie dipole są ustawione zgodnie z kierunkiem sił pola; po usunięciu pola kryształ jest w dalszym ciągu spolaryzowany - wielkość tej polaryzacji nazywa się polaryzacją szczątkową; należy przyłożyć dodatkowe pole skierowane przeciwnie, aby polaryzacja kryształu zmieniła swój kierunek - to pole nazywamy polem koercji; po osiągnięciu stanu nasycenia i zmieniając kierunek pola na przeciwny uzyskamy kompletną pętlę histerezy ferroelektrycznej,
c) właściwości próbki zależą od jej historii - występuje zjawisko histerezy temperaturowej.
Wszystki wymienione powyżej właściwości ferroelektryków wynikają z istnienia polaryzacji spontanicznej. Ferroelektryki posiadają w swojej budowie struktury zwane domenami, w których wszystkie dipole są ustawione do siebie równolegle. Domeny mogą istnieć tylko w określonym przedziale temperatur - powyżej ferroelektrycznej temperatury Curie ruch cieplny molekuł uniemożliwia istnienie domen i ferroelektryk staje się paraelektrykiem; w tej temperaturze obserwuje się także maksimum przenikalności elektrycznej.
Powyżej TC w fazie paraelektrycznej spełniona jest zależność * = C/(T-TC) ( prawo Curie - Weissa, C-stała ). W pobliżu przejścia ze stanu para- do ferroelektrycznego wystarczy pole ma silny wpływ na własności dielektryka. Polaryzacja ciał zależy nie tylko od przyłożonego pola i temperatury, lecz również od geometrii próbki.
2. Wykonanie ćwiczenia.
Dane do obliczeń:
R1=10k
R2=1M
C1=470nF
S=20mm2
d=0,8mm
W ćwiczeniu dokonano pomiaru parametrów pętli histerezy oraz pojemności elektrycznej dla próbki ferroelektryka w funkcji temperatury . W doświadczeniu należy także wyznaczyć temperaturę Curie (Tc) oraz stałą Curie. Trzeba też zaobserwować zmianę kształtu pętli histerezy ferroelektrycznej wraz ze wzrostem temperatury.
T[C] |
31,6 |
35 |
40 |
45 |
47 |
48 |
49 |
49,2 |
49,4 |
49,6 |
T[K] |
304,6 |
308 |
313 |
318 |
320 |
321 |
322 |
322,2 |
322,4 |
322,6 |
Uy |
1,1 |
1,1 |
0,95 |
0,68 |
0,58 |
0,49 |
0,38 |
0,34 |
0,32 |
0,28 |
Uc |
0,85 |
0,82 |
0,75 |
0,69 |
0,61 |
0,6 |
0,52 |
0,45 |
0,43 |
0,39 |
P[*1000C/m2] |
25,85 |
25,85 |
22,325 |
15,98 |
13,63 |
11,515 |
8,93 |
7,99 |
7,52 |
6,58 |
Ec[*1000V/m] |
1,0625 |
1,025 |
0,9375 |
0,8625 |
0,7625 |
0,75 |
0,65 |
0,5625 |
0,5375 |
0,4875 |
Cx[pF] |
26 |
28 |
34 |
40 |
125 |
300 |
320 |
320 |
300 |
250 |
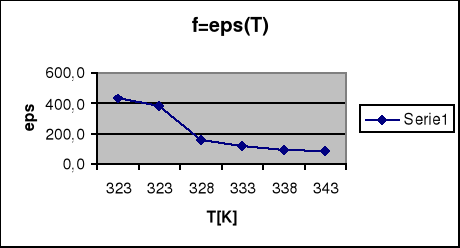
eps[*1000] |
47,0056 |
50,6215 |
61,4689 |
72,316 |
225,989 |
542,373 |
578,531 |
578,531 |
542,373 |
451,977 |
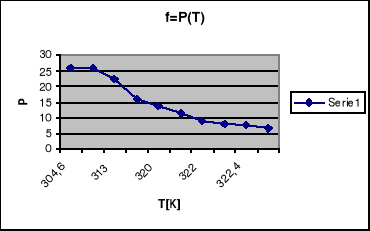
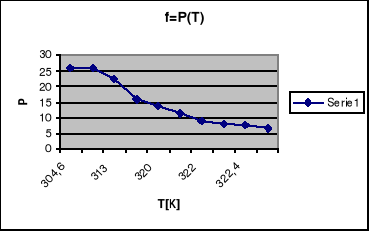
Wykres zależności polaryzacji od temperatury.
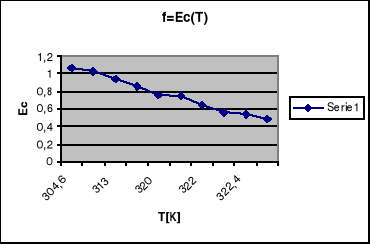
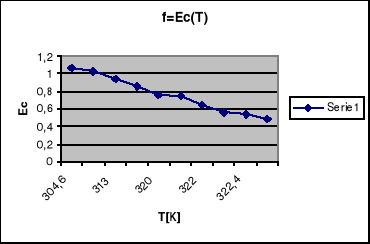
Wykres zależności pola koercji od temperatury.
Odczytana z wykresu polaryzacji temperatura Curie wynosi: 313K
T[C] |
49,8 |
50 |
55 |
60 |
65 |
70 |
T[K] |
322,8 |
323 |
328 |
333 |
338 |
343 |
Cx[pF] |
240 |
210 |
89 |
63 |
53 |
46 |
eps[*1000] |
433,9 |
379,7 |
160,9 |
113,9 |
95,8 |
83,2 |
chi[*1000] |
432,9 |
378,7 |
159,9 |
112,9 |
94,8 |
82,2 |
1/chi[*0,001] |
0,00231 |
0,002641 |
0,006254 |
0,008858 |
0,010546 |
0,012171 |
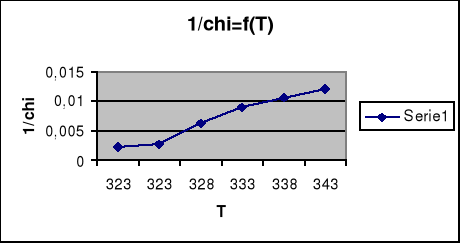
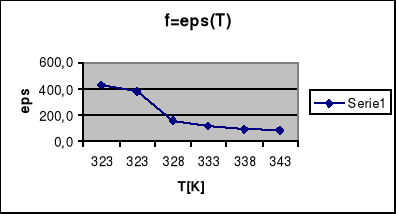
Wykres zależności f=*(T)
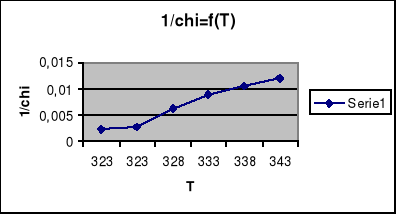
Wykres zależności odwrotności podatności elektrycznej w funkcji temperatury.
Wnioski.
W ćwiczeniu dokonano pomiarów próbki ferroelektryka . Na podstawie opracowanych wyników można zauważyć zgodność teorii z dokonanymi pomiarami . Z obserwacji pętli histerezy na oscyloskopie wynika że wraz ze wzrostem temperatury maleje polaryzacja co uwidacznia się zawężaniem pętli aż do ostatecznego przejścia w linię prostą . Również na podstawie otrzymanego wykresu zależności polaryzacji całkowitej od temperatury widać że do pewnej temperatury tzw. temp. Curie mamy wzrost polaryzacji , a nasyępnie gwałtowny spadek polaryzacji . Oznacza to że ferroelektryk staje się dielektrykiem , a temperatura w której ta zmiana zachodzi jest temp Curie i można ją z tego wykresu określić . Również wykres pola koercji w funkcji temp. wykazywał podobne zmiany co dodatkowo potwierdza badaną teorię .Wykres zależności odwrotności podatności elektrycznej od temp. potwierdza również rozważania teoretyczne . Jak zostało to przewidziane jest to zależność liniowo narastająca . Z tego wykresu można określić stałą Curie . Otrzymane z wykresów temperatury Curie dla obu przypadków wyszły podobne co oznacza prawidłowość przyjętej teorii o właściwościach ferroelektryków . Z powyższego ćwiczenia wynika więc że ferroelektryki są to materiały które poniżej temperatury Curie wykazują się właściwościami określonymi pętlą histerezy , a powyżej temp. Curie stają się dielektrykami i posiadają ich właściwości .
Wyszukiwarka
Podobne podstrony:
cw 14, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
Sprawozdanie nr 34, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
Sprawozdanie nr 12, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
Zasady tworzenia wykresów, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
Sprawozdanie nr 24, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
sprawozdanie 2 histereza, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
FIZA8, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
34 moje, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
sprawkoz dzwięku, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
wyznaczanie pracy wyjścia, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
fiz 12, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
FIZA1, m.szpaner, Semestr IV, Fizyka, Sprawozdania Fizyka
FIZ, Budownictwo, Semestr IV, Fizyka Budowli
cw 1 nasze, Politechnika Łódzka Budownictwo, Semestr IV, Fizyka budowli II, Lab
Zestawienie obciazen wg Eurokodu, STUDIA budownictwo, SEMESTR IV, fizyka budowli
beton lab 1, Semestr IV uz, Sprawozdania Dyszak, sprawozdania Doroty
więcej podobnych podstron