Sztuczna inteligencja

Raport projektu

Temat: Zrealizować sieć neuronową uczoną algorytmem wstecznej propagacji błędu z przyspieszeniem metodą momentum (learnbpm) uczącą się identyfikować spam.

Ralf Sawa

II EF-DI

L9

Spis treści

1. Przedstawienie problemu

Celem projektu było zrealizowanie sieci neuronowej, która na podstawie informacji o wiadomości e-mail potrafi ją zaklasyfikować jako spam lub zwykłą wiadomość.

Spam - niechciane lub niepotrzebne wiadomości elektroniczne. Najbardziej rozpowszechniony jest spam za pośrednictwem poczty elektronicznej (…) Zwykle (choć nie zawsze) jest wysyłany masowo.

Istotą spamu jest rozsyłanie dużej ilości informacji o jednakowej treści do nieznanych sobie osób. Nie ma znaczenia, jaka jest treść tych wiadomości. Aby określić wiadomość mianem spamu, musi ona spełnić trzy następujące warunki jednocześnie:

1. Treść wiadomości jest niezależna od tożsamości odbiorcy.

2. Odbiorca nie wyraził uprzedniej, zamierzonej zgody na otrzymanie tej wiadomości.

3. Treść wiadomości daje podstawę do przypuszczeń, iż nadawca wskutek jej wysłania może odnieść zyski nieproporcjonalne w stosunku do korzyści odbiorcy.

Dane dla zbioru uczącego sieć neuronową oraz informacje na ich temat zostały pobrane ze strony http://archive.ics.uci.edu/ml/machine-learning-databases/spambase/. Zostały one uzyskane w wyniku analizy wiadomości e-mail (prywatnych i związanych z pracą) autorów tego zbioru.

Analizie poddanych zostało 4601 wiadomości e-mail (każda wiadomość to jeden wiersz pliku z danymi), z czego 1813 stanowił spam (=39.4%), a 2788 (=60.6%) zwykłe wiadomości. Każda z tych wiadomości została opisana przy pomocy 58 atrybutów (każdy atrybut to jedna kolumna pliku z danymi), ostatni z nich świadczy o tym, że dana wiadomość jest spamem. Dane zapisane są w pliku spambase.data.

Informacje na temat atrybutów:

NR KOLUMNY	TYP DANYCH	ZAKRES DANCH	OPIS
1-48	ciągły rzeczywisty	[0..100]	Procentowy udział słowa ze słownika poniżej tabeli (wszystkich słów jest 48) w stosunku do wszystkich słów danej wiadomości.
49-54	ciągły rzeczywisty	[0..100]	Procentowy udział znaku ze zbioru poniżej tabeli (wszystkich słów jest 6) w stosunku do wszystkich znaków danej wiadomości.
55	ciągły rzeczywisty	[1,…]	Średnia długość nieprzerwanego ciągu wielkich znaków w danej wiadomości.
56	ciągły całkowity	[1,…]	Długość najdłuższego nieprzerwanego ciągu wielkich liter w danej wiadomości.
57	ciągły całkowity	[1,…]	Całkowita liczba wielkich liter w danej wiadomości.
58	symboliczny	{0, 1}	Oznacza, czy dana wiadomość jest spamem.

Słownik wyrazów: make, address, all, 3d, our, over, remove, internet: continuous, order, mail, receive, wil, people, report, addresses, free, business, email, you, credit, your, font, 000, money, hp, hpl, george, 650, lab, labs, telnet, 857, data, 415, 85, technology, 1999, parts, pm, direct, cs, meeting, original, project, re, edu, table, conference.

Zbiór znaków: ; ( [ ! $ #.

Twórcami tej bazy e-maili są Mark Hopkins, Erik Reeber, George Forman, Jaap Suermondt z Hewlett-Packard Labs, została ona stworzona na przełomie czerwca i lipca roku 1999.

2. Opis sieci neuronowej

Sieć neuronowa jest modelem matematycznym, składającym się z sieci węzłów obliczeniowych zwanych neuronami i ich połączeń. Jest to pewna technika obliczeniowo-statystyczna, należąca do dziedziny sztucznej inteligencji. Jej działanie symuluje działanie ludzkiego mózgu. Sposób połączenia sztucznych neuronów przypomina wielopołączeniową sieć neuronów w mózgu. Każdy neuron w mózgu jest połączony z około 10 tys. innych, a podczas pracy mózgu pracują wszystkie neurony jednocześnie. W sztucznej sieci neuronowej neurony łączą się tylko z sąsiadami - działają one kolejno a nie jednocześnie.

Matematycznie rzecz biorąc, dobrze skonstruowana sieć neuronowa jest w stanie "nauczyć się" aproksymować dowolną funkcję wielu zmiennych (istnieje na to dowód matematyczny). Ponieważ jest to aproksymacja, a nie interpolacja, to sieć jest w stanie uogólniać nabytą wiedzę na nieznane jej, choć podobne problemy. Tę zdolność nazywa się generalizacją. Sieć neuronowa dobrze generalizuje, kiedy odpowiedzi udzielane przez nią dla zestawu danych testowych są prawidłowe lub mieszczą się w granicach ustalonego błędu. Dane testowe muszą pochodzić z tej samej populacji co dane wykorzystane do uczenia sieci.

Sztuczny neuron jest systemem przetwarzającym wartości sygnałów wprowadzanych na jego wejścia w pojedynczą wartość wyjściową

Rysunek 1 Budowa sztucznego neuronu

- wektor sygnałów wejściowych

- wektor wag

f - funkcja aktywacji

y - sygnał wyjściowy

Sygnał wyjściowy neuronu wyraża się wzorem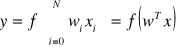
, gdzie f to odpowiednia funkcja aktywacji.

Algorytmem uczenia sieci neuronowej w tym projekcie jest uczenie pod nadzorem metodą wstecznej propagacji błędu z przyspieszeniem metodą momentum (learnbpm). Zgodnie z tym algorytmem, wektor błędu sieci obliczany dla warstwy wyjściowej rzutowany zostaje wstecz poprzez kolejne jej warstwy. Umożliwia to obliczenie nowych wartości współczynników wagowych poszczególnych warstw, a w efekcie zmniejszenie średniokwadratowego błędu sieci. W pierwszej kolejności wyliczany jest błąd ostatniej warstwy, w oparciu o sygnały wyjściowy i wzorcowy. W pozostałych warstwach błąd obliczany jest jako ustalona funkcja błędu neuronów warstwy poprzedzającej. Algorytm ten należy do gradientowych metod optymalizacji, gdyż opiera się o stwierdzenie, że gradient funkcji wskazuje kierunek jej najszybszego wzrostu a zmieniając jego znak na przeciwny, uzyskujemy kierunek najszybszego spadku funkcji. Możemy w ten sposób minimalizować funkcję celu przez modyfikację jej zmiennych, w przypadku sieci - współczynników wagowych, w kierunku najszybszego spadku funkcji. Zmiana wartości współczynników wagowych i progowych dla i -tego wejścia i - tego neuronu opisana jest zależnością:

?W(i,j) = mc*?Wp(i,j) + (l-mc)*lr*d(i)*p(j)

?B(i) = mc*?Bp(i) + (l - mc)*Lr*d(i)

Parametr mc (stała momentum) określa wpływ poprzedniej zmiany wag ?Wp i współczynników progowych ?Bp na zmianę dokonywaną obecnie. Zastosowanie metody momentum przyczynia się do likwidacji zbyt gwałtownych zmian wartości funkcji błędu sieci. Umożliwia to bezpieczne zwiększenie wartości współczynnika prędkości uczenia Lr.

Wywołanie:

[dW,dB] = learnbpm (P,D,LR,MC,dW,dB)

Argumenty:

P - macierz wektorów wejściowych (wymiar R*Q, R - liczba wejść warstwy, Q -

ilość wektorów),

D - macierz pochodnych błędów warstwy (wymiar S*Q, S - liczba neuronów w

warstwie),

LR - współczynnik prędkości uczenia,

MC - wartość stałej momentum,

dW - macierz przyrostów współczynników wagowych warstwy w poprzednim kroku (wymiar

S*R),

dB - wektor przyrostów współczynników progowych warstwy w poprzednim kroku (wymiar

S*1)

Wartości zwracane:

dW - nowa macierz przyrostów współczynników wagowych warstwy (wymiar S*R),

dB - nowa macierz przyrostów współczynników progowych warstwy (wymiar S*1)

3. Skrypt realizujący uczenie sieci

Przed wczytaniem danych najpierw przygotowania zostaje przestrzeń Matlaba. Wyłączone zostają ostrzeżenia oraz usunięte zostają dane z obszaru roboczego, zamknięte wszystkie aktualnie wyświetlane wykresy oraz okno poleceń:

clc %wyczyszczenie okna poleceń clear all %wyczyszczenie przestrzeni close all %zamknięcie aktualnie wyświetlanych wykresów nntwarn off %wyłączenie ostrzeżeń warning off

Wczytanie danych z pliku spambase.data

xx = load('spambase.data'); j = 1; for i=1:15:length(xx(:,1)) temp(j,:) = xx(i,:); j=j+1; end clear xx xx = temp; for i = 1:(length(xx(1,:))-1) for j = 1:length(xx(:,1)) P(j,i) = xx(j,i); end end T=xx( :,length(xx(1,:)) );

Plik zostaje wczytany do zmiennej xx, jest to macierz o 4601 wierszach i 58 kolumnach. Po wczytaniu danych następuje rozdzielenie atrybutów wiadomości od ostatniej kolumny zawierającej informację o tym czy dana wiadomość jest spamem, czy też nie, zatem jest do wektor wyjściowy sieci. Zostaje ona zapisana do wektora T. Pozostałe dane zostają zapisane w zmiennej P jako macierz wektorów wejściowych. W badaniach sieci nie zostały wzięte pod uwagę wszystkie dane tylko ich część, ze względu na długi czas obliczeń przy wprowadzaniu wszystkich danych.

Wartości wczytanych danych znacznie się od siebie różnią, dlatego przed podaniem ich na wejście sieci zostają one znormalizowane. Normalizacja danych wykonywana jest poprzez znalezienie maksymalnego elementu w kolumnie, a następnie podzielenie wszystkich elementów tej kolumny przez tę wartość, przeprowadzana jest zgodnie z poniższym skryptem:

for i=1:length(P(1,:)) maks(i) = max(P(:,i)); if (maks(i) == 0) maks(i) = 0.01; end for j=1:length(P) P(j,i) = P(j,i)/maks(i); end end

Główna część programu:

T = transpose(T); %transponowanie macierzy T P = transpose(P); %transponowanie macierzy P [R,Q] = size(P); %ustawienie rozmiarów wejścia, R liczba wierszy, Q liczba kolumn [S3,Q] = size(T); %ustawienie rozmiarów wyjścia, %S3 liczba wierszy macierzy wejścia, Q liczba kolumn S1=11; %ustawienie liczby neuronów w warstwie S1 S2=7; %ustawienie liczby neuronów w warstwie S2 lr=0.01; %współczynnik uczenia mc=0.9; %stała momentum err_goal=0.1; %docelowy błąd %zainicjalizowanie neuronów i ich współczynników wagowych, dodatkowy komentarz pod listingiem [W1,B1] = nwtan(S1,R); [W2,B2] = nwtan(S2,S1); [W3,B3] = rands(S3,S2); %stworzenie tablic wypełnionych zerami dW1=zeros(size(W1)); dW2=zeros(size(W2)); dW3=zeros(size(W3)); dB1=zeros(size(B1)); dB2=zeros(size(B2)); dB3=zeros(size(B3)); disp_freq=100; %częstotliwość wyświetlania wyników max_epoch=30000; %liczba kroków uczenia error=[]; %wektor zawierający błędy kolejnych kroków uczenia A1 = tansig(W1*P,B1); %obliczenie wyjscia dla sieci, z funkcją aktywacji tansig A2 = tansig(W2*A1,B2); A3 = purelin(W3*A2,B3); %obliczenie wyjscia dla sieci, W1*P+B1 z funkcją aktywacji purelin E = T-A3; %oblicznie błędu pomiędzy wzorcem a wyjściem z sieci SSE = sumsqr(E); %oblicznie funkcji celu, czyli sumy z kwadratów błędów %wykonanie algorytmu uczenia sieci dla podanej liczby kroków uczenia for epoch=1:max_epoch, %ewentualne zakończenie gdy funkcja celu jest mniejsza od minimalnego błędu if SSE < err_goal, epoch=epoch-1; break; end, %obliczenie wektorów błędów warstw wyjściowych D3 = deltalin(A3,E); D2 = deltatan(A2,D3,W3); D1 = deltatan(A1,D2,W2); %obliczenie zmian wag przy uczeniu algorytmem propagacji wstecznej momentum [dW1,dB1] = learnbpm(P,D1,lr,mc,dW1,dB1); [dW2,dB2] = learnbpm(A1,D2,lr,mc,dW2,dB2); [dW3,dB3] = learnbpm(A2,D3,lr,mc,dW3,dB3); %aktualizacja wag W1 = W1 + dW1; B1 = B1 + dB1; W2 = W2 + dW2; B2 = B2 + dB2; W3 = W3 + dW3; B3 = B3 + dB3; %obliczenie wyjscia z sieci dla nowych wag A1 = tansig(W1*P,B1); A2 = tansig(W2*A1,B2); A3 = purelin(W3*A2,B3); E = T-A3; SSE = sumsqr(E); %tworzenie funkcji celu, zapisywanie do wektora error jego aktualnej wartości %i nowej wartosci funkcji celu error = [error SSE]; %wyświetlanie wykresu i informacji o przebiegu uczenia if (rem(epoch,disp_freq) == 0) message = sprintf('Epoch: %g/%g, Err_goal: %g, SSE: %g, ANS: %g \n',epoch,max_epoch,err_goal,SSE, 100*(1-sum((abs(T-A3)>.5)')/length(T))); fprintf(message,0); plot(1:length(T),T,'r',1:length(T),A3,'g'); legend('Wartosci rzeczywiste','Wartosci wyuczone',1); pause(1e-100); end end

nwtan - generowanie macierzy wag I wektora biasu przy użyciu metody Nguyen-Widrow do inicjalizacji ich wartości dla warstwy tan-sigmoid

[W1,B1] = nwtan(S1,R);

Stworzona zostaje macierz W1 o wymiarach S1 x R i wektor B1 o wymiarze S1.

rands - generowanie macierzy wag i wektora biasu o wartościach statycznych o jednorodnym rozkładzie z zakresu [-1,1].

[W3,B3] = rands(S3,S2);

Stworzona zostaje macierz W3 o wymiarach S3 x S2 i wektor B3 o wymiarze S3.

4. Eksperymenty

Eksperymenty przeprowadzane były w następujący sposób:

Dla pewnej liczby danych wejściowych ustalano parametry

S1=20;

S2=10;

lr=0.1;

mc=0.9;

Epoch: 100/30000, Err_goal: 0.01, SSE: 6.95054e+295, ANS: 0 Epoch: 200/30000, Err_goal: 0.01, SSE: NaN, ANS: 100 Epoch: 300/30000, Err_goal: 0.01, SSE: NaN, ANS: 100

Jeżeli wartość funkcji celu rosła (SSE), zmniejszany był współczynnik uczenia lr (learning rate).

lr=0.01

Epoch: 100/30000, Err_goal: 0.01, SSE: 74.4358, ANS: 60.5863 Epoch: 200/30000, Err_goal: 0.01, SSE: 73.3101, ANS: 60.5863 Epoch: 300/30000, Err_goal: 0.01, SSE: 73.3094, ANS: 60.5863 Epoch: 400/30000, Err_goal: 0.01, SSE: 73.3094, ANS: 60.5863 Epoch: 500/30000, Err_goal: 0.01, SSE: 73.3094, ANS: 60.5863 Epoch: 600/30000, Err_goal: 0.01, SSE: 73.3094, ANS: 60.5863

Jeżeli wartość funkcji celu nadal nie malała lub malała w zbyt wolnym tempie, ponownie zmniejszano współczynnik uczenia.

Następnie manipulowano ilością neuronów w warstwach, w celu uzyskania jak najlepszego wyniku.

Epoch: 29700/30000, Err_goal: 0.01, SSE: 1.32136, ANS: 99.6743 Epoch: 29800/30000, Err_goal: 0.01, SSE: 1.31344, ANS: 99.6743 Epoch: 29900/30000, Err_goal: 0.01, SSE: 1.30556, ANS: 99.6743 Epoch: 30000/30000, Err_goal: 0.01, SSE: 1.29772, ANS: 99.6743

Po kilku eksperymentach ze stałą momentum, postanowiono zostawić ją na poziomie 0,9.

Dla ustawień

S1 = 11;

S2 = 7;

lr = 0.01;

mc = 0.9;

osiągano najlepsze rezultaty uczenia sieci:

Epoch: 6784/30000, Err_goal: 0.1, SSE: 0.1000, ANS: 100

5. Podsumowanie i wnioski

Celem projektu było poznanie struktur sieci neuronowych zbudowanych z wielu warstw na przykładzie programu realizującego sieć neuronową uczoną algorytmem wstecznej propagacji błędu z przyspieszeniem metodą momentum rozpoznającego spam. Dane do uczenia sieci zostały pobrane ze strony http://archive.ics.uci.edu/ml/machine-learning-databases/spambase/. Przed rozpoczęciem procesu budowania sieci dane te były normalizowane, ponieważ przyjmowały wartości z szerokiego zakresu.

Przy realizacji projektu nie udało się wykorzystać wszystkich danych dostępnych w pliku spambase.data z powodu zbyt niskiej, dostępnej dla realizatora projektu mocy obliczeniowej. Liczne zmiany parametrów uczenia przy czasie jednego toku uczenia sieci sięgającym kilku godzin oraz brak zadowalających efektów zmusiły autora do zawężenia zbioru danych wejściowych. Jednak nawet przy dużo krótszym czasie obliczeń, ustalenie parametrów uczenia było czasochłonne, przy czym nie została odkryta żadna zależność pomiędzy wielkością parametrów, a ostatecznym wynikiem. Parametrami, którymi manipulowano w celu nauczenia sieci z odpowiednim błędem były ilość neuronów w warstwach S1 i S2, współczynnik uczenia, stała momentum oraz ilość danych wejściowych. Stabilność procesu uczenia kontrolowano współczynnikiem uczenia, a następnie poszukiwano odpowiednich ilości neuronów w warstwach w celu osiągnięcia jak najlepszego wyniku.

Ostatecznie, metodą wielu prób i błędów, został osiągnięty zadowalający wynik stu procentowego nauczenia sieci przy oczekiwanym błędzie 0,1.

Sieć neuronowa okazuje się być obiecującym narzędziem do rozpoznawania niepożądanych wiadomości e-mail, ponieważ nie jest znana bezpośrednia zależność pomiędzy zwykłymi wiadomościami e-mail, a spamem. Wyuczenie sieci na odpowiednio dużym zbiorze danych stworzyłoby dobrą podstawę silnego systemu antyspamowego.

Źródło: http://pl.wikipedia.org/wiki/Spam

9

---