Politechnika Łódzka 10.05.1999

Filia w Bielsku - Białej

Wydział Fizyki Technicznej

Informatyki i Matematyki Stosowanej

Kierunek Informatyka

Rok I / Semestr II

LABORATORIUM

Z FIZYKI

ĆWICZENIE NUMER 66

Wyznaczanie stałej Plancka metodą fotoelektryczną .

Skład grupy :

Olgierd Fałat

Waldemar Friedrich

Adrian Głąbek

1. Cel ćwiczenia

Celem obecnego ćwiczenia jest wyznaczenie stałej Plancka oraz pracy wyjścia , dla materiału z którego wykonana jest katoda , wykorzystując zjawisko fotoelektryczne zewnętrzne .

2. Wstęp teoretyczny

Promieniowanie elektromagnetyczne ( np. światło ) padając na powierzchnię ciał może wybić z nich wolne elektrony , jeśli promieniowanie to posiada odpowiednią energię . Mamy wtedy do czynienia z tzw. zjawiskiem fotoelektrycznym zewnętrznym . Zjawisko fotoelektryczne zewnętrzne jest dowodem na korpuskularny charakter światła gdyż doświadczenia wykazały , że :

• elektrony zostają wybijane , jeżeli częstotliwość padającego światła ν jest większa od pewnej wartości granicznej ν₀

• liczba wybitych elektronów nie zależy od natężenia padającego światła

co jest sprzeczne z falową teorią światła .

Energia przekazywana jest porcjami zwanymi kwantami energii - niemożliwe jest dostarczenie tylko części kwantu energii . Część energii padającego światła zwana pracą wyjścia W potrzebna jest do tego aby elektron mógł być wybity z powierzchni metalu .

Zjawisko fotoelektryczne zewnętrzne opisuje równanie Einsteina-Millikana :

gdzie : h to stała Plancka

ν to częstość padającego promieniowania

W to tzw. praca wyjścia

E_kin to energia kinetyczna jaką uzyska wybity elektron

Stała Plancka jest uniwersalną stałą fizyczną wynoszącą w przybliżeniu 6,6256 * 10^-34 [ Js ] .

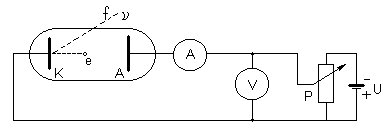
Stałą tą możemy wyznaczyć posługując się poniższym układem .

Fotony światła monochromatycznego f o częstotliwości ν padając na katodę K wybijają z nie elektrony e , które to po wybiciu posiadają pewną energię kinetyczną E_kin . Źródło zasilania w połączeniu z potencjometrem P zapewnia regulację napięcia od 0 do U . Podłączenie potencjału dodatniego do katody K i ujemnego do anody A powoduje , że wybity elektron jest hamowany i przy odpowiednio dużym napięciu nie dotrze on do anody ( wtedy to prąd anodowy będzie wynosił 0 ) . Wtedy to energia kinetyczna elektronu E_kin równa się co do wartości iloczynowi napięcia hamującego U₀ i ładunku elektronu . Powyższy wzór przyjmie wtedy postać :

=>
=>

Jak widać wartość napięcia hamującego U₀ jest funkcją zmiennej ν o charakterze liniowym ( y = ax +b ) . Obliczając wartości parametrów a i b będzie można później obliczyć stałą Plancka i pracę wyjścia .

3. Przebieg ćwiczenia

Do przeprowadzenia danego doświadczenia posłużyliśmy się następującymi przyrządami :

• źródłem światła monochromatycznego o regulowanej długości fali

• odpowiednim przyrządem do badania zjawiska fotoelektrycznego

• woltomierzami

W pierwszym etapie przeprowadzania doświadczenia zdjęliśmy charakterystykę prądową w funkcji częstotliwości (długości fali ) I_a = f (ν ) dla długości fal z zakresu 400 do 600 nm . Długość fali zmienialiśmy co 20 nm . Układ pomiarowy nie zawierał jednak przyrządu do pomiaru natężenia prądu lecz tylko woltomierz więc musieliśmy dokonać odpowiednich przeliczeń :

=>

Rezystancja R w naszym przypadku wynosiła 2,49 MΩ . Przykładowe obliczenie :

I = 0,0556 / 2490000 = 2,233 * 10^-8 A = 22,33 nA

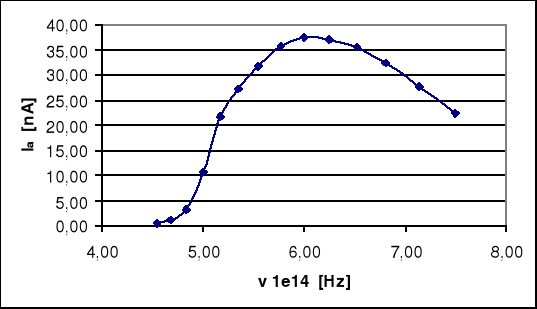
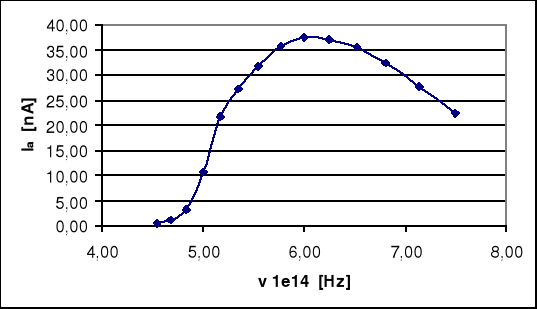
Poniższa tabela zawiera charakterystykę prądową .

TABELA nr 1

λ	nm	400	420	440	460	480	500	520	540	560	580	600	620	640	660
ν	Hz	7,50* 10^14	7,14*10^14	6,81*10^14	6,52*10^14	6,25*10^14	6,00*10^14	5,77*10^14	5,55*10^14	5,35*10^14	5,17*10^14	5,00*10^14	4,84*10^14	4,68*10^14	4,54*10^14
I	nA	22,33	27,71	32,29	35,58	36,99	37,35	35,74	31,69	27,15	21,61	10,56	3,21	1,08	0,40

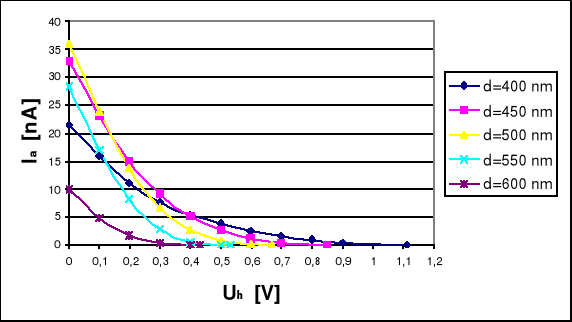
Następnie dla określonych długości fal ( 400 nm , 450 nm , 500 nm , 550 nm , 600 nm ) zdjęliśmy krzywe hamowania tj. po ustawieniu danej długości fali nastawialiśmy początkowo napięcie hamowania na 0 ( U_h = 0 V , maksymalny prąd anodowy ) i mierzyliśmy wartość prądu anodowego . Napięcie zwiększaliśmy co 0,1 V i powtarzaliśmy pomiary ( zmiany co 30 s ) . W końcowym etapie serii pomiarów odczytywaliśmy wartość napięcia hamującego przy którym prąd anodowy wynosił 0 nA . Poniższa tabela zawiera zależność prądu anodowego od danego napięcia hamującego I_a = f ( U_h ) ( dla różnych długości fal ) .

TABELA nr 2

λ = 400 nm		λ = 450 nm		λ = 500 nm		λ = 550 nm		λ = 600 nm
Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia	Uh	Ia
V	nA	V	nA	V	nA	V	nA	V	nA
0,0	21,37	0,0	33,01	0,0	36,06	0,0	28,27	0,0	9,88
0,1	15,86	0,1	23,21	0,1	23,98	0,1	16,95	0,1	4,78
0,2	11,04	0,2	14,94	0,2	13,86	0,2	8,19	0,2	1,65
0,3	7,63	0,3	9,16	0,3	6,67	0,3	2,81	0,3	0,36
0,4	5,42	0,4	5,26	0,4	2,69	0,4	0,64	0,4	0,02
0,5	3,82	0,5	2,77	0,5	0,80	0,5	0,04	0,433	0,00
0,6	2,53	0,6	1,24	0,6	0,16	0,533	0,00
0,7	1,61	0,7	0,44	0,667	0,00
0,8	0,88	0,847	0,00
0,9	0,40
1,113	0,00

Na podstawie uzyskanych danych wykreśliliśmy zależność I_a = f ( ν )

Następnie wykreśliliśmy zależność I_a = f ( U_h ) dla poszczególnych długości fal .

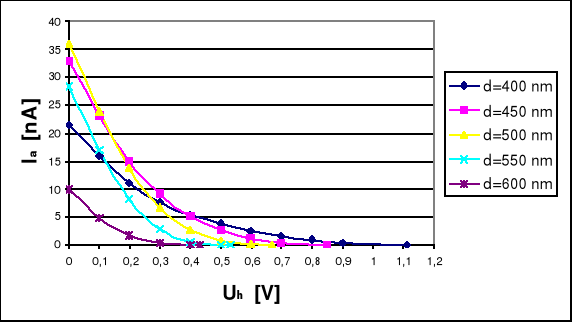
Wykorzystując wyniki z tabeli nr 2 sporządziliśmy tabelę nr 3 , która zawiera wartości napięcia hamującego U_h0 przy którym I_s = 0 .

TABELA nr 3

λ	nm	400	450	500	550	600
Uh0	V	1,113	0,847	0,667	0,535	0,433

Korzystając z powyższych danych przy pomocy programu komputerowego obliczamy współczynniki funkcji liniowej U_h0 = aν + b .

a = 2,72 * 10^-15 [ Js/C ] = [ Vs ]

b = -0,94 [ V ]

Wiedząc , że :

a = h / e

W = -b / e

możemy obliczyć stałą Plancka oraz pracę wyjścia .

h = a * e = 2,72 * 10^-15 * 1,60 * 10^-19 = 4,35 * 10^-34 [ Js ]

W = -b / e = - ( -0,94 ) / 1,60 * 10^-19 = 5,89 * 10¹⁸ [ J ] = 0,94 [ eV ]

e = 1,6 * 10^-19 [ C ]

4. Podsumowanie

Otrzymany przez nas wynik odbiega od faktycznej wartości stałej Plancka wynoszącej 6,6256 * 10^-34 [ Js ] . Związane jest to zapewne z niedokładnościami pomiarowymi i dokładnością aparatury pomiarowej .

---