Wyznaczanie granicznego przewodnictwa równoważnikowego elektrolitów mocnych i słabych
Marcin Górski	Data:
Mirosław Dziergowski	Zaliczenie:

1. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie granicznych przewodnictw elektrolitów mocnych i słabych.

2. Zasada pomiaru.

Graniczne przewodnictwo równoważnikowe elektrolitów mocnych można wyznaczyć w oparciu o zależność:

,gdzie:

- przewodnictwo równoważnikowe,

- przewodnictwo równoważnikowe graniczne,

a - stała,

c - stężenie elektrolitu.

Pomiar przewodnictwa elektrolitów wykonuje się metodą Kohlrauscha, która polega na wyzna-czeniu oporu naczynka przy użyciu mostka Wheatstone'a.

Pomiar składa się z dwóch części. W pierwszej z nich wyznacza się tzw. s t a ł ą n a c z y n k a (k). W tym celu wprowadza się roztwór KCl o znanym przewodnictwie właściwym w żądanej temperaturze do naczynka pomiarowego. Pomiar daje opór cieczy wzorcowej, skąd można wyz-naczyć stałą naczynka.

W obliczeniach szczególnie dla roztworów o małym przewodnictwie, należy uwzględnić przewod-nictwo wody użytej do przygotowania roztworów (wynika to z dysocjacji wody, rozpuszczenia dwutlenku węgla, wymycia alkaliów ze szkła).

W analogiczny sposób należy zmierzyć przewodnictwo roztworów: CH₃COONa, HCl, NaCl.

3. Schemat urządzenia pomiarowego.

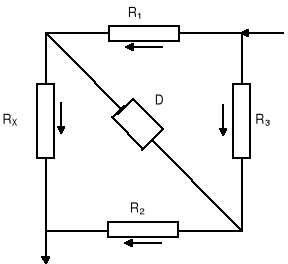
4. Wyniki pomiarów.

T = 25^oC k = 0,528

Stężenie	CH3COONa			HCl			NaCl
	G [Ω^-1]	κ [Ω^-1⋅cm^-1]	Λ [Ω^-1⋅cm^2⋅ g-równ.^-1]	G [Ω^-1]	κ [Ω^-1⋅cm^-1]	Λ [Ω^-1⋅cm^2⋅ g-równ.^-1]	G [Ω^-1]	κ [Ω^-1⋅cm^-1]	Λ [Ω^-1⋅cm^2⋅ g-równ.^-1]
3,125⋅10^-3	6,9⋅10^-4	3,62⋅10^-4	115,960	2,5⋅10^-3	1,32⋅10^-3	421,750	8⋅10^-4	4,20⋅10^-4	134,544
6,25⋅10^-3	1,27⋅10^-3	6,69⋅10^-4	106,974	5,23⋅10^-3	2,76⋅10^-3	441,484	1,44⋅10^-3	7,58⋅10^-4	121,334
1,25⋅10^-2	2,38⋅10^-3	1,25⋅10^-3	100,369	1,015⋅10^-2	5,36⋅10^-3	428,544	2,75⋅10^-3	1,45⋅10^-3	115,996
2,5⋅10^-2	4,12⋅10^-3	2,17⋅10^-3	86,930	2,005⋅10^-2	1,058⋅10^-2	423,341	5,21⋅10^-3	2,75⋅10^-3	109,948
5⋅10^-2	6,16⋅10^-3	3,25⋅10^-3	65,005	3,75⋅10^-2	1,98⋅10^-2	395,925	9,85⋅10^-3	5,19⋅10^-3	103,968
10^-1	1,32⋅10^-2	6,97⋅10^-3	69,670	7,4⋅10^-2	3,91⋅10^-2	390,665	1,945⋅10^-2	1,02⋅10^-2	102,667

5. Obliczenia.

1. Obliczenie stałej naczynka oraz przewodnictwa właściwego i równoważnikowego badanych elektrolitów.

1. Stałą naczynka (k) wyznaczamy wg. zależności:

,gdzie

κ_wz - przewodnictwo właściwe 0,01M roztworu KCl w temp. 25^oC

G_wz - przewodnictwo roztworu KCl

G_wody - przewodnictwo wody destylowanej użytej do przygotowania roztworów.

2. Przewodnictwo właściwe (κ) i przewodnictwo równoważnikowe (Λ) obliczamy we wzorów:

(1)

(2)

,gdzie κ - przewodnictwo właściwe

k - stała naczynka

G - przewodnictwo roztworu

G_wody - przewodnictwo wody destylowanej użytej do przygotowania roztworów.

Λ - przewodnictwo równoważnikowe

C_równ. - stężenie wyrażone w gramorównoważnikach [g-równ./cm³].

Obliczenia przykładowe (dla roztworu CH₃COONa).

Dane
Stała naczynka	k	5,28⋅10^-1
Przewodnictwo wł. KCl	κ	1,413⋅10^-3
Przewodnictwo H2O	Gwody	3,62⋅10^-6

Z zależności (1) obliczamy κ:

dla C = 3,125⋅10^-3 κ = 5,28⋅10^-1⋅(6,90⋅10^-4 - 3,62⋅10^-6) = 3,62⋅10^-4 [Ω^-1⋅cm^-1].

dla C = 6,25⋅10^-3 κ = 5,28⋅10^-1⋅(1,27⋅10^-3 - 3,62⋅10^-6) = 6,69⋅10^-4 [Ω^-1⋅cm^-1].

dla C = 1,25⋅10^-2 κ = 5,28⋅10^-1⋅(2,38⋅10^-3 - 3,62⋅10^-6) = 1,25⋅10^-3 [Ω^-1⋅cm^-1].

dla C = 2,5⋅10^-2 κ = 5,28⋅10^-1⋅(4,12⋅10^-3 - 3,62⋅10^-6) = 2,17⋅10^-3 [Ω^-1⋅cm^-1].

dla C = 5⋅10^-2 κ = 5,28⋅10^-1⋅(6,16⋅10^-3 - 3,62⋅10^-6) = 3,25⋅10^-3 [Ω^-1⋅cm^-1].

dla C = 10^-1 κ = 5,28⋅10^-1⋅(1,32⋅10^-2 - 3,62⋅10^-6) = 6,97⋅10^-3 [Ω^-1⋅cm^-1].

Przeliczenie stężenia molowego na równoważnikowe:

Zgodnie ze wzorem:

1 mol CH₃COONa posiada masę molową 82 [g/mol], czyli 1 g-równ. tego związku będzie posia-dał taką samą masę molową jaką posiada 1 mol.

Z zależności (2) obliczamy Λ:

dla C = 3,125⋅10^-3 Λ=

dla C = 6,25⋅10^-3 Λ=

dla C = 1,25⋅10^-2 Λ=

dla C = 2,5⋅10^-2 Λ=

dla C = 5⋅10^-2 Λ=

dla C = 10^-1 Λ=

Dla elektrolitów HCl i NaCl obliczamy κ z zależności (1) i Λ z zależności (2) w analogiczny spo-sób jak wyżej.

2. Obliczenie granicznego przewodnictwa równoważnikowego dla kwasu octowego (CH₃COOH).

Ponieważ kwas octowy jest słabym elektrolitem nie można, więc wyznaczyć graficznie dla niego przewodnictwa równoważnikowego granicznego, gdyż w tym przedziale stężeń wykres nie będzie liniowy. Aby obliczyć Λ_∞ CH₃COOH wykorzystamy wcześniej wyznaczone doświadczalnie przewodnictwa równoważnikowe graniczne mocnych elektrolitów (CH₃COONa, HCl, NaCl).

Zgodnie z prawem niezależnej wędrówki jonów, graniczne przewodnictwo równoważnikowe dla kwasu octowego można zapisać wzorem:

Elektrolity mocne można zapisać:

Dodatkowo znając przewodnictwo równ. graniczne dla NaCl można obliczyć Λ_∞ CH₃COOH z zależności

Dane:
Elektrolit	Λ∞
CH3COONa	96,119
HCl	423,811
NaCl	123,085

Niektóre równoważnikowe przewodnictwa jonowe w rozcieńczeniu niekończenie wielkim w temperaturze 25^oC.
H^+	349,7
Na^+	50,1
Cl^-	76,6
CH3COO^-	40,8
Elektrolit	Λ∞	Λ∞
	Wartość obliczona w t = 25^oC	Wartość tablicowa w t = 25^oC
CH3COONa	96,119	90,9
HCl	423,811	426,3
NaCl	123,085	126,7
CH3COOH	396,845	390,5

VI. Wnioski.

Zarówno przewodnictwo równoważnikowe Λ, jak i przewodnictwo właściwe κ zależą w dużej mierze od stężenia i temperatury.

Badając zależność przewodnictwa właściwego od stężenia elektrolitu mocnego można wysnuć wniosek, że przewodnictwo właściwe rośnie ze wzrostem stężenia. Wzrost ten wywołany być może zwiększeniem liczby jonów będących nośnikami prądu elektycznego. Wielkości te nie są jednak do siebie wprost proporcjonalne. Przewodnictwo właściwe rośnie bowiem wolnej niż stężenie.

Przyczyną zmniejszania się przewodnictwa równoważnikowego mocnych elektrolitów wraz ze wzrostem stężenia jest nie tylko siła wynikająca z istnienia spadku potencjału pomiędzy elektroda-mi, ale również inne siły hamujące ruch jonów.

Te siły hamujące ruchy jonów można wyjaśnić za pomocą teorii Debye'a i Hueckela. Założeniem tej teorii (w przypadku mocnych elektrolitów o małych stężeniach) jest tworzenie się chmur elektronowych w roztworze co powoduje obniżenie przewodnictwa, w stosunku do tego, które byłoby, gdyby jony zachowywały pełną indywidualność i swobodę. Natomiast w przypadku mocnych elektolitów w roztworach bardziej stężonych skutkiem zmniejszania się przewodnictwa jest występowanie tzw. efektu relaksacyjnego i elektroforetycznego. Efekt elektroforetyczny, polega na tym, że jon centralny porusza się wraz ze swoją otoczką dipoli wodnych w środowisku, które nie znajduje się w stanie spoczynku. Ponieważ w chmurze jonowej znajdują się przeważnie jony przeciwnego znaku niż znak jonu centralnego, to poruszają się one wraz ze swoimi otoczkami dipoli wodnych w przeciwnym kierunku niż rozpatrywany jon. Na skutek tego dochodzi do wystąpienia dodatkowych sił tarcia. Natomiast drugi efekt, efekt relaksacyjny jest procesem tworzenia się chmury jonowej i jej zanikania pod wpływem ruchu jonów. Gdy prędkość tworzenia się tej chmury jonowej i prędkość jej zanikania są nieskończenie duże wówczas prowadzi to do zburzenia symetrii chmury, jej średnia gęstość ładunku zmniejsza się przed jonem, a zwiększa za nim. W związku z tym chmura jonowa zaczyna wywierać wpływ elektrostatyczny hamujący i jest on tym większy im większa jest prędkość poruszającego się jonu.

Schemat mostka Wheatstone'a

R₁ R₂ R₃ R_X - opory

D - detektor

---