Wydział: MECH. DIAGNOSTYKA I REMONTY MASZYN I URZĄDZEŃ OKRĘTOWYCH |
PRACOWNIA FIZYCZNA
|
Rok szkolny: 98/99 |
Nr ćwiczenia: 6
|
Temat: Badanie efektu Halla
|
Data oddania : 04.16. 99r.
|
Wykonał :
|
Sprawdził: |
Ocena: |
I CZĘŚĆ TEORETYCZNA
Koncentrację swobodnych nośników ładunku wyznaczamy na podstawie efektu Halla. Polega ona na tym, że w materiale przewodzącym prąd elektronowy i dziurowy pod działaniem pola magnetycznego powstaje pole elektryczne o kierunku prostopadłym do kierunku przewodzenia prądu.
Prostopadłościenna płytka o przewodnictwie wysoko elektronowym lub dziurowym umieszczona jest w polu magnetycznym o indukcji Bz.
Na poruszające się elektrony lub dziury działa siła Lorentza F=q• (r • B) o wartości liczbowej Fy=qr • Bz. Wywołuje ona przesuwanie ładunków wzdłuż osi y, ładując jedną ściankę o powierzchni ah dodatnio, drugą ujemnie. Powstaje pole elektryczne Ey. W stanie równowagi siły pola elektrycznego i magnetycznego, działające na ładunek wzdłuż osi y są równe.
Układ pomiarowy do wyznaczania stałej Halla
Stałą R=1/qn nazywamy stałą Halla. Dla elektronów przyjmuje ona wartość ujemną, dla dziur dodatnią. Znak stałej Halla pozwala więc określić charakter przewodzenia w danym materiale. Wartość liczbowa stałej Halla określa koncentrację swobodnych nośników ładunku n=1/Re
Do wyznaczania stałej Halla posługujemy się układem przedstawionym na rys. Przez selenoid o długości l, średnicy 2r, ilości zwojów N, przepuszczany prąd o natężeniu I. Indukcja magnetyczna w środku solenoidu wynosi
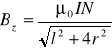
Do środka wprowadzamy płytkę germanową w sposób pokazany na rysunku i przepuszczamy przez nią prąd Ix. Napięcie Halla Uy mierzymy woltomierzem.
II OBLICZENIA
I [A] |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
B [T] |
0,06 |
0,08 |
0,11 |
0,14 |
0,17 |
0,2 |
0,23 |
0,26 |
0,29 |
0,32 |
0,36 |
0,39 |
0,42 |
0,45 |
0,48 |
UH=Ix=20mA |
0,08 |
0,14 |
0,2 |
0,26 |
0,31 |
0,36 |
0,41 |
0,47 |
0,5 |
0,52 |
0,6 |
0,65 |
0,69 |
0,75 |
0,78 |
UH=Ix=40mA |
0,14 |
0,24 |
0,33 |
0,41 |
0,49 |
0,56 |
0,64 |
0,72 |
0,77 |
0,85 |
0,93 |
1 |
1,05 |
1,1 |
1,17 |
1,6 |
1,7 |
1,8 |
1,9 |
2 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
3,0 |
0,52 |
0,54 |
0,57 |
0,6 |
0,64 |
0,67 |
0,7 |
0,73 |
0,76 |
0,79 |
0,83 |
0,86 |
0,89 |
0,92 |
0,95 |
0,83 |
0,87 |
0,91 |
0,96 |
0,99 |
1,05 |
1,08 |
1,09 |
1,11 |
1,17 |
1,2 |
1,25 |
1,28 |
1,3 |
1,33 |
1,22 |
1,29 |
1,32 |
1,4 |
1,45 |
1,5 |
1,56 |
1,61 |
1,65 |
1,7 |
1,75 |
1,8 |
1,85 |
1,9 |
1,95 |
0,5 A
Ix [mA] |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
UH [V] |
0,08 |
0,17 |
0,24 |
0,31 |
0,37 |
0,43 |
0,48 |
0,5 |
0,52 |
0,57 |
1 A
Ix [mA] |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
UH [V] |
0,16 |
0,32 |
0,48 |
0,57 |
0,68 |
0,78 |
0,86 |
0,92 |
0,95 |
1 |
1,5 A
Ix [mA] |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
UH [V] |
0,21 |
0,39 |
0,62 |
0,8 |
0,94 |
1,05 |
1,15 |
1,25 |
1,3 |
1,4 |
![]()
1. Obliczam stałą Halla dla poszczególnych wartości Ix, UH i B.
Wiedząc że 1/ne=RH można zapisać
![]()
i stąd
![]()
Dane:
d= 0,006 m d= 0,006 m
UH, B
I= 0,02 A I= 0,04 A
![]()
RH0,2= 0,45
RH0,4= 0,557 RH0,4= 0,439
RH0,6= 0,540 RH0,6= 0,42
RH0,8= 0,542 RH0,8=0,415
RH1,0= 0,487 RH1,0= 0,398
RH1,2= 0,5 RH1,2= 0,384
RH1,4= 0,5 RH1,4= 0,366
RH1,6= 0,478 RH1,6=0,351
RH1,8= 0,478 RH1,8= 0,347
RH2,0= 0,464 RH2,0= 0,339
RH2,2= 0,462 RH2,2= 0,334
RH2,4= 0,438 RH2,4= 0,325
RH2,6= 0,433 RH2,6= 0,316
RH2,8= 0,431 RH2,8= 0,311
RH3,0= 0,42 RH3,0= 0,307
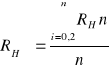
![]()
Dla Ix= 20 mA RHŚr= 0,370 - dla Ix= 40 mA
![]()
2. Obliczam prędkość nośników ładunku
![]()
Obliczam prędkość nośników ładunku dla I= 1A i Ix= 20 mA
![]()
3. Obliczam błąd metodą różniczki zupełnej
f(x, y, z) dI= 0,01A; dB= 0,01 T; du= 0,05 V
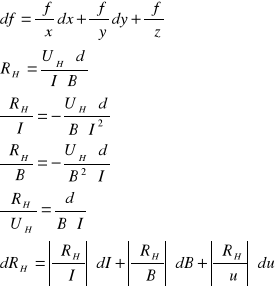
dla UH= 0,52; B= 0,32; I= 0,02
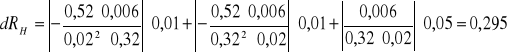
![]()
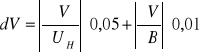
![]()
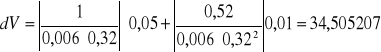
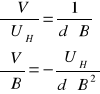
![]()
![]()
![]()
![]()
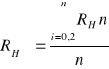
![]()
![]()
![]()
![]()
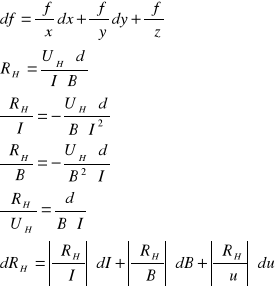
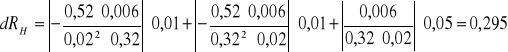
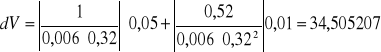
![]()
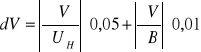
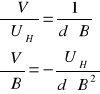
![]()
Wyszukiwarka
Podobne podstrony:
AKCELE~2, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1, FIZA, FIZAII
AOL2, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, PODSTAWY KON, Program do obliczeń
Diesel engine, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, Szkoła moje
MP, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, kwity, SEMESTR II, EPEC
A4, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, PODSTAWY KON, Program do obliczeń P
Badanie tyrystorów, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELEKTRA
Praca Piotra, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, III
Zabezpieczenia, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELEKTRA
BADANI~4, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELEKTRA, ELEKTRA
SWIAT~42, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, III, AUTO
Łopatki, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, AM2, Siłownie, Maszyny przepły
tab lam, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, PODSTAWY KON, Program do oblic
ciasne22, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, PODSTAWY KON, Projekt, Pkm
POMIA~68, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, III, TECH REM
Montaz ukladu tlokowo korbowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1,
ELEKTRA-EGZAM, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELEKTRA
Silnik asyn. pierścieniowy, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELE
Stefanowski- Układ zdalnego sterowania i zabezpieczeń, Akademia Morska -materiały mechaniczne, szkoł
więcej podobnych podstron