Cel ćwiczenia:

Celem danego ćwiczenia jest wyznaczenie współczynnika przewodnictwa cieplnego badanego materiału.

Wstęp teoretyczny:

Zjawisko przewodnictwa cieplnego w ciałach stałych polega na transporcie energii w postaci ciepła w ciele ogrzanym w sposób nierównomierny. Jeżeli będziemy ogrzewać cało i w tej samej chwili odbierać od niej ciepło z tą samą prędkością, to taki ustalony rozkład temperatury w ciałach nazywamy stanem stacjonarnym.

Podstawowym równaniem fizycznym opisującym przewodnictwo cieplne w tym przypadku jest równanie Fouriera.

Wzór 1. Równanie Fouriera opisujące przewodnictwo cieplne

Gdzie Q oznacza ilość ciepła przechodzącą w jednostce czasu przez jednorodną warstwę o grubości Δx i powierzchni S przy różnicy temperatur ΔT.

We wzorze tym
jest współczynnikiem charakteryzującym środowisko (właściwości), w którym występuje przepływ ciepła. Nazywa się go współczynnikiem przewodnictwa cieplnego lub przewodnością cieplną.

W ogólnym przypadku temperatura T w różnych punktach ciała zmienia się z upływem czasu T =f(x,y,x,t). Stan taki wystąpi, np. gdy w wyżej opisanym przykładzie szybkość dostarczania ciepła i odbierania z drugiej strony rozpatrywanej warstwy są różne. Funkcję T określa się rozwiązując równanie przewodnictwa cieplnego, które dla jednorodnego izotopowego ciała bez wewnętrznych źródeł ciepła przyjmuje postać

Wzór 2. sposób zmieniania się temperatury w ciele badanym

Wielkość a charakteryzuje szybkość wyrównania się temp i nosi nazwę współczynnika wyrównania temp. Współczynnik a ma znaczenie fizyczne zredukowanego współczynnika przewodnictwa cieplnego i związany jest z wielkością
następującym wzorem

ρ - gęstość ciała

c - ciepło właściwe, równe co do wartości ilości ciepła w J potrzebnej do ogrzania masy 1 kg ciała o1K.

Wartość współczynnika
można wyznaczyć doświadczalnie za pomocą wzoru 1 mierząc bezpośrednio Q,S, ∆T, ∆x. Okazuje się jednak, że spośród czterech wymienionych wielkości ilość ciepła Q jest wielkością, której bezpośrednie zmierzenie nastręcza szereg trudności. Dlatego też niżej posługujemy się metoda Christiansena, która omija te trudności.

Proponowana metoda nosi nazwę metody Christiansena. Jest to metoda porównawcza, w której porównuje się współczynnik przewodzenia ciepła badanego materiału ze współczynnikiem innego (wzorcowego) materiału, dla którego wartość
jest znana. Tym samym mierzenie ilości ciepła Q nie jest konieczne. Zasada tej metody jest następująca: dwie płytki zrobione z materiałów o współczynnikach
_o (znany) i
_x (nieznany) umieszcza się miedzy równoległymi ściankami o różnych temperaturach, które nie ulegają zmianie w czasie doświadczenia. Jeśli grubość płytek d_o i d_x są małe (w porównaniu z ich powierzchnią), to w ich środkowej części strumień cieplny jest prostopadły do powierzchni i nie zależy od obecności bocznych granic (brzegów płytek). Dla cienkich płytek powierzchnia obszaru niezakłóconego strumienia bliska jest całkowitej powierzchni płytki S i z dużą dokładnością może być do niej przyrównywana. W tym wypadku na podstawie wzoru 2 można napisać

stąd

Przyrząd Christiansena schematycznie pokazany jest na rysunku 1. Jest to system składający się z grzejnika o temperaturze T₁ i chłodnicy o temperaturze T₂. Temperatura T₁ wytwarzana jest przez przepływ wody podgrzewanej w termostacie, a T₂ przez przepływ wody z sieci wodociągowej. Strumień cieplny przechodzi od grzejnika do chłodnicy przez zaciśnięte między nimi płytki (krążki) z badanego i wzorcowego materiału.

Opracowanie wyników pomiarów:

Tabela 1. Wyniki pomiarów

Temperatura	[mV]	[mV]
30ºC	1,17 - 0,85 = 0,32	0,86 - 0,29 = 0,57
45ºC	1,44 - 0,99 = 0,45	1,01 - 0,25 = 0,76

- różnica napięć na przeciwległych ściankach płytki znanej (plexiglas)

- różnica napięć na przeciwległych ściankach płytki badanej (textolit)

₀ = 0,17[kcal/msdeg]^.10^3.4,1863[J] = 711,67 [W/m^.K]

1) Obliczam różnicę temperatury ∆T_o dla przeciwległych ścian płytki znanej i obliczam różnicę temperatury ∆T_x dla przeciwległych ścian płytki badanej. [wykorzystywane dane z Tabeli 1]

a) Obliczenia dla temperatury 30^oC:

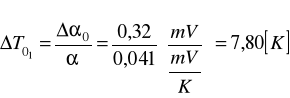
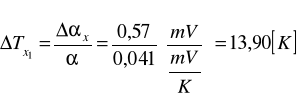
b) Obliczenia dla temperatury 45^oC:

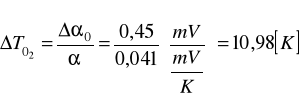
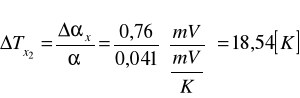
2) Obliczam współczynnik przewodnictwa cieplnego badanej płytki:

a) W temperaturze 30^oC:

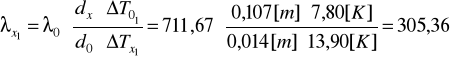
b) Obliczenia dla temperatury 45^oC:

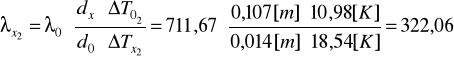
3) Obliczam błąd względny graniczny w_z1 i w_z2 odpowiednio dla wyliczonych współczynników przewodnictwa cieplnego
_x1 i
_x2:

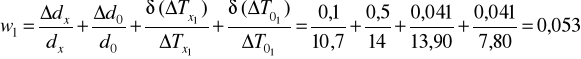
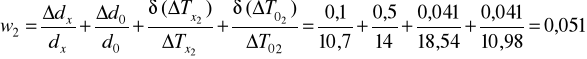
4) Obliczam błąd bezwzględny b₁ i b₂ odpowiednio dla wyliczonych współczynników przewodnictwa cieplnego
_x1 i
_x2:

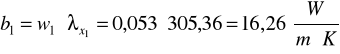
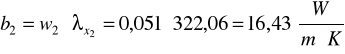
Wnioski:

Ćwiczenie miało na celu wyznaczenie współczynnika przewodnictwa cieplnego metodą Christiansena. Jest to metoda porównawcza, z czego między innymi mogą wynikać błędy. Wpływ na pomiary miały również dokładność pomiarów szerokości płytek oraz błędne odczytanie napięcia. Z obliczeń wynika: przy pierwszym pomiarze ( dla 30^oC) współczynnik przewodnictwa cieplnego wynosi 305,36
wynik jest obarczony błędem bezwzględnym równym 16,26
; w drugim pomiarze (dla 45^oC) współczynnik przewodnictwa cieplnego wynosił 322,06
z błędem bezwzględnym 16,43
.

---