WSTĘP TEORETYCZNY:
Stałą szybkości reakcji nazywamy współczynnik proporcjonalności k w równaniu kinetycznym.
W klasycznej kinetyce przyjmuje się, że stała k jest niezależna od stężenia reagentów i czasu reakcji, natomiast zmienia się z temperaturą i zależy od rodzaju i stężenia katalizatorów. Stała szybkości wyraża liczbowo szybkość reakcji, gdy stężenie każdego z substratów wynosi 1 mol/l. Wymiar stałej zależy od postaci równania kinetycznego i wyraża się ogólnym wzorem:
Jodowanie acetonu jest reakcją autokatalizowaną przez jony wodorowe, będące jednym z jej produktów:
Jest to reakcja dwustopniowa, następcza:
Etap I
Etap II
Etap I jest powolny, odwracalny i decydujący o szybkości całej reakcji. Przebieg jego jest następujący:
postać ketonowa postać enolowa
W rezultacie szybkość całej reakcji zależy od stężenia acetonu (a-x) i kwasu (b+x), a nie zależy od stężenia jodu. Reakcja jodowania acetonu jest reakcją drugiego rzędu i szybkość jej możemy wyrazić następującym wzorem:
lub po scałkowaniu:
gdzie:
k - stała szybkości
a - początkowe stężenie acetonu
b - początkowe stężenie jonów wodorowych
x - ubytek stężenia acetonu (równy przyrostowi stężenia kwasu) po czasie t
Energią aktywacji nazywamy minimum energii jaką powinny być obdarzone cząsteczki, aby mogły przereagować. Można ją obliczyć na podstawie równania Arrheniusa:
A - współczynnik częstotliwości
Energię aktywacji można również obliczyć znając dwie stałe szybkości danej reakcji w dwóch różnych temperaturach ze wzoru:
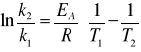
lub badając nachylenie prostej w układzie współrzędnych lg k = f(1/T).
WYNIKI:
Dla roztworu A 40mlHCl
t |
Vt |
x |
a-x |
b+x |
ln(a(b+x})/(b(a-x)) |
|
0 |
16,2 |
0 |
0,109 |
0,16 |
0 |
|
15 |
15,8 |
1E-04 |
0,1089 |
0,1601 |
0,001543 |
|
30 |
14,1 |
0,000525 |
0,108475 |
0,160525 |
0,008104 |
|
45 |
13,5 |
0,000675 |
0,108325 |
0,160675 |
0,010422 |
|
60 |
13 |
0,0008 |
0,1082 |
0,1608 |
0,012354 |
|
75 |
12,5 |
0,000925 |
0,108075 |
0,160925 |
0,014287 |
|
90 |
10 |
0,00155 |
0,10745 |
0,16155 |
0,023963 |
|
105 |
8,35 |
0,001963 |
0,107038 |
0,161963 |
0,03036 |
|
120 |
7,25 |
0,002238 |
0,106763 |
0,162238 |
0,034629 |
|
135 |
6,5 |
0,002425 |
0,106575 |
0,162425 |
0,037541 |
|
Dla roztworu B:20 ml HCl
t |
Vt |
x |
a-x |
b+x |
ln(a(b+x})/(b(a-x)) |
|
0 |
16 |
0 |
0,109 |
0,08 |
0 |
|
15 |
14,4 |
0,0004 |
0,1086 |
0,0804 |
0,008664 |
|
30 |
13,5 |
0,000625 |
0,108375 |
0,080625 |
0,013533 |
|
45 |
13,3 |
0,000675 |
0,108325 |
0,080675 |
0,014614 |
|
60 |
13,25 |
0,000688 |
0,108313 |
0,080688 |
0,014884 |
|
75 |
12,5 |
0,000875 |
0,108125 |
0,080875 |
0,018938 |
|
90 |
8,35 |
0,001913 |
0,107088 |
0,081913 |
0,041327 |
|
105 |
8,25 |
0,001938 |
0,107063 |
0,081938 |
0,041865 |
|
120 |
8 |
0,002 |
0,107 |
0,082 |
0,043212 |
|
135 |
7,5 |
0,002125 |
0,106875 |
0,082125 |
0,045904 |
|
OPRACOWANIE WYNIKÓW:
I.Obliczenia dla roztworu A
Podstawiając do wzoru kolejno każdą otrzymaną wartość otrzymujemy wykres obrazujący zależność zmian stężenia w czasie
![]()
gdzie:
k - stała szybkości
a - początkowe stężenie acetonu
b - początkowe stężenie jonów wodorowych
x - ubytek stężenia acetonu (równy przyrostowi stężenia kwasu) po czasie t
Stężenia początkowe acetonu a i kwasu b, zostały obliczone na podstawie zależności:
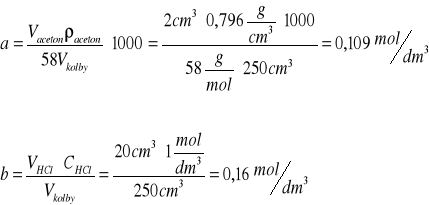
Ubytek stężenia acetonu „x” (i równy mu przyrost stężenia kwasu) po upływie czasu t obliczamy w oparciu o równanie reakcji redukcji jodu tiosiarczanem i reakcję jodowania acetonu. Ubytek ten jest dwukrotnie mniejszy od ubytku tiosiarczanu, a więc: od różnicy ilości moli Na2S2O3 zużyte na początku (Vo) i po upływie czasu t (V1) na zmiareczkowanie nadmiaru jodu
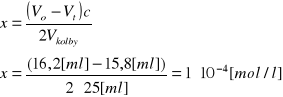
gdzie Vo i Vt to ilości Na2S2O3 zużyte na zmiareczkowanie 25 cm3 mieszaninie reagującej na początku reakcji (t=0) i po czasie t, c - stężenie Na2S2O3 w mol/dm3
Analogicznieobliczam ubytek stężenia acetonu dla pozostałych próbek otrzymuje wykres
z powyższego wykresu odczytuje współczynnik kierunkowy prostej: a'=0,00025. Na tej podstawie obliczam stałą szybkości k
y= a'x
Podczas eksperymentu badano stałą szybkości reakcji jodowania acetonu w stałej temperaturze (298,15 K) dla dwu mieszanin reakcyjnych o różnym stężeniu kwasu solnego (35 ml HCl i 25 ml HCl). Wartości tych stałych wynoszą odpowiednio:
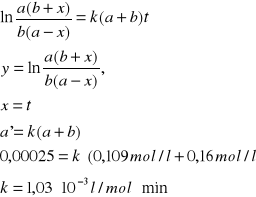
II.Obliczenia dla roztworu B
a=0,109[mol/l]
obliczam stężenie kwasu b
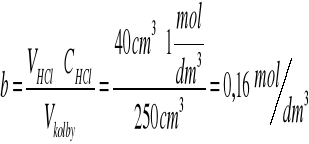
obliczam ubytek stężenia acetonu (x) wg wzoru:
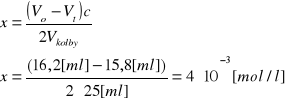
z powyższego wykresu odczytuję a' i obliczam k
y = a'x
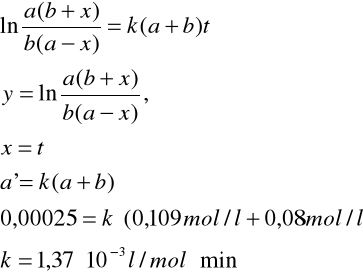
WNIOSKI:
Stała szybkości procesu jodowania acetonu w roztworze zawierającym 20 ml
![]()
1 M HCl wynosi
natomiast stała szybkości tego procesu w roztworze zawierającym 40 ml HCl jest mniejsza i wynosi
![]()
Reakcja jodowania acetonu jest reakcją drugiego rzędu i zależy m.in od stężenia jonów wodorowych w roztworze. Szybkość powyższej reakcji wskazuje ,że przebiega ona szybciej , gdy jonów wodorowych jest mniejzatem nie są one katalizatorem tej reakcji są jednym z produktów i wraz ze wzrostem ich stężenia reakcja biegnie wolniej.
2
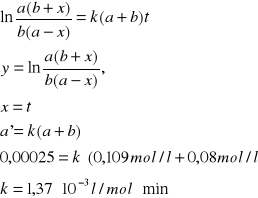
![]()
![]()
Wyszukiwarka
Podobne podstrony:
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
spr57, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Moje 50 , Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
monia 11, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spr
15 wyznaczanie ciepła spalania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chem
KOND41vmac, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II s
rad, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
spr15, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
Do druku askorbinowy, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczn
Elektroda szklana, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna c
Podczas wymuszonego przep+éywu p+éynu, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wsz
27 poprawa 2, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, Chemia fizyczna
POLSKI, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spraw
spr26, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy
lab50as, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II spra
hk spr numer 23, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz
11 wyznaczanie ciepła rozpuszczania, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy,
więcej podobnych podstron