Łukasz Dębiński

ĆWICZENIE 6 (3.2)

Wyznaczanie oporu elektrycznego metodą mostka Wheatstone'a.

Charakterystyczną cechą metali jest wysoka przewodność elektryczna. Własność tę można wyjaśnić na podstawie elektronowej teorii przewodnictwa metali. Klasyczna teoria oparta jest na modelu przedstawiającym metal jako przestrzeń utworzoną przez jony sieci krystalicznej, w której poruszają się swobodne elektrony, zwane również elektronami przewodnictwa.

W sieci krystalicznej, elektrony zewnętrznej powłoki atomowej znajdują się pod wpływem działania jądra macierzystego i jąder sąsiednich atomów. Ponieważ rozmiary sieci są tego samego rzędu wiel- kości co średnice atomów, to siły działające na elektrony walencyjne równoważą się. Ta wzajemna kompensacja działań powoduje, że elektrony walencyjne nie są związane z żadnym atomem, tworzą więc gaz elektronowy, któremu przypisuje się cechy gazu doskonałego.

Elektrony swobodne poruszają się w metalu chaotycznie, z różnymi prędkościami, zderzając się węzłami sieci krystalicznej.

Wielkością charakteryzującą metal pod względem przewodzenia prądu elektrycznego jest opór R.

Na podstawie poniższego wzoru opór nie zależy od napięcia oraz od natężenia przepływającego prądu, natomiast jest on związany z geometrycznymi rozmiarami przewodnika i wielkościami opisującymi stan gazu elektronowego w metalu.

m - masa elektronu;

- średnia prędkość między zderzeniami;

l - długość przewodnika;

S - pole przekroju przewodnika;

e - ładunek elektronu;

nO - liczba swobodnych elektronów;

- średnia droga swobodna;

Ze względów praktycznych opór przewodnika wyraża się wzorem:

ρ - opór właściwy;

W układzie SI opór przewodnika mierzony jest w omach (Ω).

Z prawa Ohma
wynika, że opór przewodnika jest równy jednemu omowi, jeżeli pod napięciem jednego wolta przez przewodnik płynie prąd o natężeniu jednego ampera.

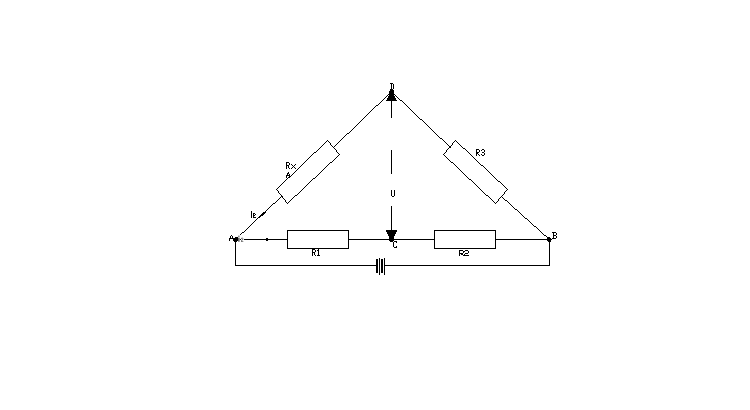
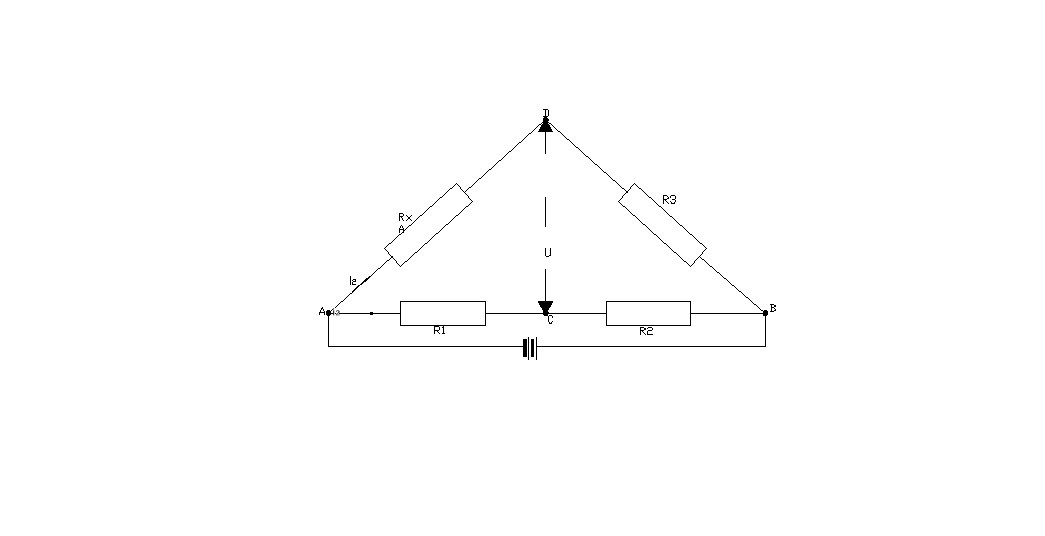
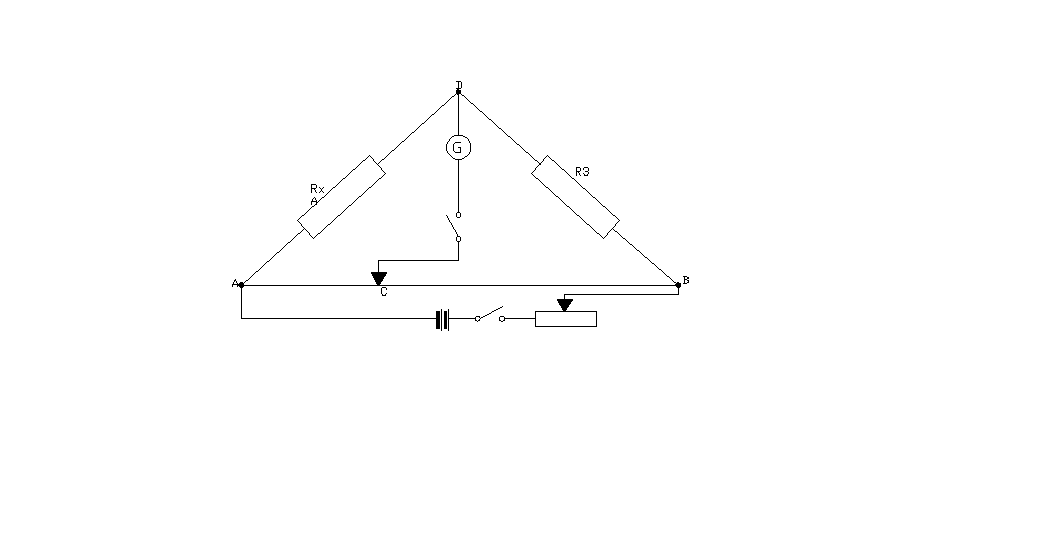
Charakteryzując przewodnik pod względem zdolności przewodzenia prądu należy wyznaczyć jego przewodność elektryczną lub opór. Można tego dokonać między innymi za pomocą mostka Wheatstone'a. Jego schemat ideowy jest przedstawiony poniżej.

W górną gałąź mostka włączone są opory: wzorcowy R3 i badany RX, natomiast dolną stanowią opory R1 i R2. Do punktów A i B dołączone jest źródło prądu stałego. W obwodzie mostka wyróżnia się dwa obwody, zawierające elementy ε, R3 i RX oraz ε, R1 i R2, dla których drugie prawo Kirchoffa ma postać:

Napięcie U między punktami C i D jest równe zeru, jeśli wartości oporów będą spełniały równanie:

zwane warunkiem zerowania lub równowagi mostka. Wskaźnikiem może być galwanometr włączony między punktami C i D, który wskaże natężenie prądu iG=0, jeżeli mostek będzie zrównoważony.

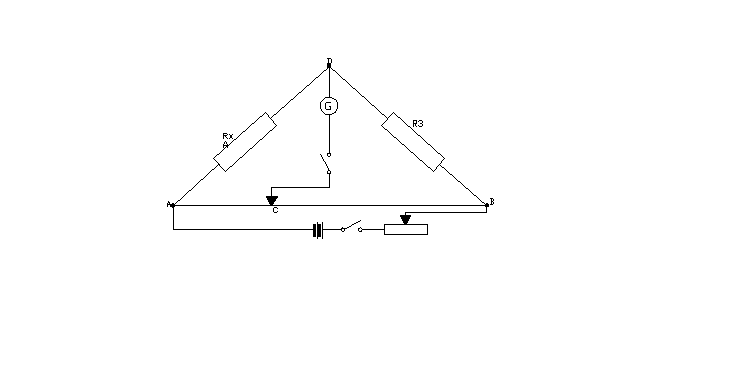
W ćwiczeniu opór R3 ( rysunek powyżej) jest oporem dekadowym, natomiast rolę oporów R1 i R2 spełnia drut oporowy o długości „l”. Ustawiając suwak w takie położenie C, przy którym prąd przez galwanometr G nie płynie, oraz oznaczając przez „a” długość odcinka AC, opory R1 i R2 są określone następująco:

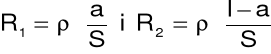
Po podstawieniu powyższych wartości do wzoru:

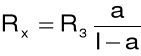
otrzymamy:

Mostkiem Wheatstone'a można mierzyć opory o wartościach od kilku omów do kilkudziesięciu megaomów, z dokładnością do setnych części procenta.

POMIARY I WYNIKI

1

3

---