Układem nazywamy wydzielony obszar przestrzenny w którym zachodzą wszystkie procesy podlegające badaniom, analizie i ujęciu w postaci bilansu ciepła, masy i energii. Nieustalone pole temperatury ( nie temperatur !) to zależność funkcyjna w której zmienną zależną jest wartość temperatury a zmiennymi niezależnymi współrzędne położenia i czas. Jeżeli pole jest stacjonarne (ustalone) to zależy wyłącznie od współrzednych, czyli nie zależy od czasu. Można też powiedzieć, że stacjonarny oznacza: niezmienny w czasie.

gradientu temperatury definiowane jest ogólnie za pomocą pochodnej

gradT =
a dla ustalonego, liniowego pola temperatury

{ T= f(x) } w postaci: gradT =
Gęstość strumienia cieplnego „q” jest to ilość ciepła wymieniana przez jednostkową powierzchnię ciała odniesiona do jednostki czasu, czyli:
gdzie: F - pole powierzchni [ m ²] przez którą przepływa elementarne ciepło dQ, dQ - elementarne ciepło [ J ],
- czas [ s ].

a)
- współczynnik przewodzenia ciepła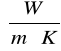
,

b) c - ciepło właściwe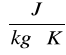
,c)
- gęstość masy

W skład warunków jednoznaczności wchodzą:

1. warunki geometryczne, określające kształt badanego układu lub części w której zachodzi badany proces cieplny, 2. warunki fizyczne, opisujące właściwości ( parametry) termofizyczne wszystkich podobszarów układu ( np. metalu odlewu, materiału formy, materiału izolacyjnego),

3. warunki początkowe, określające pole temperatury układu w momencie przyjętym jako początkowy (
= 0 ), przy czym występują one tylko w procesach nieustalonego przepływu ciepła, w których występuje nieustalone pole temperatury. Warunki brzegowe:Warunki brzegowe 1. go rodzaju (WB1r) polegają na ujęciu rozkładu temperatury na powierzchni kontrolnej układu ( tzw. temperatura powierzchni) w rozpatrywanym zakresie czasowym, czyli na zadaniu funkcji ogólnego typu

Przypadkiem szczególnym i najczęściej stosowanym są tzw. ustalone warunki brzegowe( niezmienność temperatury powierzchni) co można zapisać w postaci:
co oznacza niezmienność temperatury na powierzchni układu ( indeks „pow”) w czasie trwania procesu wymiany ciepła ( [1] - s. 30).Warunki brzegowe 3. go rodzaju (WB3r) polegają na zadaniu temperatury otoczenia układu oraz na zadaniu prawa wymiany ciepła z otoczeniem. W najczęściej stosowanym przypadku kinetykę procesu cieplnego ujmuje tzw. współczynnik wymiany ciepła użyty przez Newtona w równaniach opisujących gęstość strumienia cieplnego. Rozróżnia się tu dwa przypadki :

-dla procesu stygnięcia układu
,

-dla procesu nagrzewania

gdzie:
- współczynnik wymiany ciepła

- temperatura otoczenia.

oporem przewodzenia ciepła: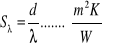

W odniesieniu do warunków brzegowych 3. rodzaju (WB3r) wprowadzono tzw. opór wymiany ciepła, równy:

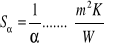
W przypadku ścianki wielowarstwowej (WB1r) w mianowniku równania (4) wystąpi suma wszystkich oporów cieplnych S_λ.

W przypadku przepływu ciepła - rozpatrywanego z wykorzystaniem WB3r -

w mianowniku równania wystąpi suma wszystkich oporówcieplnych( S _α , S _λ ).

Równanie różniczkowe opisujące ustalone, liniowe temperatury ma postać:

Wynika stąd wartość gradientu temperatury:

gradT =

gdzie:T_1pow,T_2pow - temperatury obu powierzchni ścianki płaskiej,

g - grubość ścianki ( oznaczana często przez „ d ” ).

Zgodnie z prawem Fouriera

.q = - λ gradT otrzymujemy dla ścianki płaskiej

lub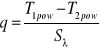

Postać równania uzyskano przy założeniu znajomości warunków brzegowych 1. Rodzaju (WB1r) W przypadku ścianki wielowarstwowej (WB1r) w mianowniku równania (4) wystąpi suma wszystkich oporów cieplnych S_λ.

W przypadku przepływu ciepła - rozpatrywanego z wykorzystaniem WB3r -

w mianowniku równania (4) wystąpi suma wszystkich oporów cieplnych ( S _α , S _λ ). Współczynnik wyrównywania temperatury definiowany jest wzorem:

współczynnik akumulacji ciepła określony jest zależnością:

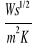
Rozwiązaniem równania ( 1 ) jest funkcja opisująca pole temperatury półprzestrzeni, zwana ( co wynika z postaci matematycznej) funkcją błędów Gaussa ( er f = error function):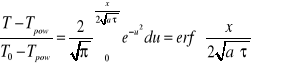

0.0 0.6 1.2 1.8 2.4 3.0

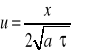
Podstawową wielkością fizyczną wynikającą z równania (5) jest gęstość strumienia cieplnego, przy czym do bilansu cieplnego istotna jest jej wartość na powierzchni kontrolnej. Po wyznaczeniu gradientu (pochodnej) i zastosowaniu prawa Fouriera

otrzymamy dla powierzchni ( x = 0) bardzo ważny wzór na wartość strumienia cieplnego :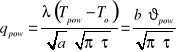

-(małe theta) spiętrzenie (różnica) temperatury [K] , (różnica rozpatrywanej temperatury i początkowej, „minimalnej” temperatury układu)

- bezwymiarowa temperatura , definiowana dla WB1r ( inaczej dla WB3r !) wzorem: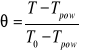

1.0

0.8

0.6

0.4

0.2

0.0

---