I. Siły zachowawcze.
Definicja I
Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej, jest równa zeru. Siła jest niezachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po drodze zamkniętej, nie jest równa zeru.
Definicja II
Siłę nazywamy zachowawczą, jeżeli praca wykonana przez nią nad punktem materialnym poruszającym się pomiędzy dwoma punktami zależy tylko od tych punktów, a nie od kształtu łączącej je drogi. Siłę nazywamy niezachowawczą, jeżeli praca wykonana przez tę siłę nad punktem materialnym poruszającym się pomiędzy dwoma punktami, zależy od kształtu drogi łączącej te punkty.
Powyższe definicje są równoważne i używa się jednej z nich w zależności od tego, która jest wygodniejsza. (np. wprowadzenie pojęcia energii potencjalnej będzie wygodniejsze, jeżeli skorzysta się ze stwierdzenia o niezależności pracy od kształtu drogi; z definicji I, gdzie mowa o drodze zamkniętej, wynika, że energia kinetyczna nie ulega zmianie, gdy działają siły zachowawcze).
Siły zachowawcze:
- siła sprężysta, wywierana przez idealną sprężynę (ciało ściska sprężynę, a potem wraca do położenia pierwotnego)
- siła ciężkości (jeśli rzucimy piłkę do góry, to wróci on do naszych rąk z taką samą energią kinetyczną, jaką miała na początku [opór powietrza pomijamy])
- siła elektrostatyczna
- inne siły działające w ten sam sposób
II. Siły niezachowawcze.
Siły niezachowawcze:
- siła tarcia (rozprasza energię)
- siła indukcji działająca w betatronie (urządzenie do przyspieszania elektronów do wysokich prędkości)
- inne siły działające w ten sam sposób
Tylko wówczas, gdy nie działają siły niezachowawcze albo kiedy pomijamy pracę przez nie wykonaną, możemy przyjąć założenie o zachowaniu energii mechanicznej.
W przypadku sił tarcia energia mechaniczna zostaje przekształcona w ciepło. Wytworzona energia cieplna jest równa pracy wykonanej przez ciało.
ΔE + Q = 0 (suma energii mechanicznej i cieplnej układu nie zmienia się).
III. Energia kinetyczna.
Energia kinetyczna jest energia ciała związaną z jego ruchem.
Praca wykonana przez wypadkową siłę F działającą na punkt materialny jest równa zmianie energii kinetycznej tego punktu.
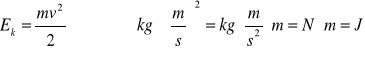
Energią kinetyczną ciała nazywamy połowę iloczynu masy tego ciała przez kwadrat jego prędkości.
Energia kinetyczna ciała znajdującego się w ruchu jest równa pracy, jaką może wykonać to ciało, zanim się zatrzyma. Energia kinetyczna jest skalarem, jej jednostką jest dżul.
IV. Energia potencjalna.
Energia potencjalna zależy tylko od położenia punktu materialnego. Nie można jej przyporządkować ciału odosobnionemu, lecz należy ją traktować jako własność całego układu.
Każda zmiana energii kinetycznej (Ek) układu jest równoważona przez zmianę energii potencjalnej (Ep) układu, tak że ich suma pozostaje stała przez cały czas trwania ruchu:
Ek + Ep = const
Energia potencjalna przedstawia pewną formę nagromadzonej energii, która może być całkowicie odzyskana i zamieniona na energię kinetyczną. (energii potencjalnej nie można kojarzyć z siłą niezachowawczą).
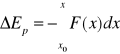
W przypadku ruchu jednowymiarowego, gdy punkt materialny porusza się od x0 do x, energię potencjalną możemy obliczyć:
gdzie F(x) - siła zachowawcza
![]()
Można też zapisać zależność między siłą a energią potencjalną:
(Energia potencjalna jest to funkcja położenia, której ujemna pochodna daje wyrażenie na siłę.)
Energię potencjalną ciała znajdującego się w punkcie odniesienia, czyli Ep(x0), przyjmujemy jako równą zero.
Energia potencjalna dla siły grawitacyjnej:
Ep = mgh
Grawitacyjna energia potencjalna na powierzchni Ziemi jest równa zeru i wzrasta liniowo wraz z wysokością h.
![]()
Energia potencjalna dla siły (sprężystej) przywracającej równowagę rozciągniętej sprężyny:
k - współczynnik sprężystości sprężyny
x - odległość, na jaką rozciągnięto sprężynę
Energia kinetyczna ciała jest równa pracy, którą może ono wykonać do chwili zatrzymania się. Wyraża się ją przy pomocy wzoru Ek = ½mv2. Nie można jednak podać ogólnej formuły wyrażającej energię potencjalną. Energia potencjalna układu ciał jest równa pracy, którą ten układ może wykonać zmieniając względne położenie swoich części, czyli zmieniając swój stan. W każdym przypadku musimy określić, jaką pracę może wykonać układ przechodząc z jednego stanu do innego i potraktować tę pracę jako różnicę energii potencjalnej układu między tymi dwoma stanami.
Zasada zachowania energii mechanicznej
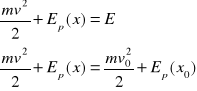
Suma energii potencjalnej i kinetycznej pozostaje wielkością stałą podczas ruchu punktu materialnego.
E - całkowita energia mechaniczna
V. Zasada zachowania energii.
Całkowita energia, tzn. suma energii kinetycznej, potencjalnej, cieplnej i wszystkich innych rodzajów energii nie zmienia się. Energia może być przekształcona z jednej formy energii w inną, ale nie może być stwarzana, ani zniszczona; energia całkowita jest wielkością stałą.
Ek + Ep + Q + (inne formy energii) = const
ΔEk + ΔEp + ΔQ + (Δ inne formy energii) = 0
Energia kinetyczna i potencjalna jest zachowywana tylko w przypadku działania sił zachowawczych. Energia całkowita jest zachowywana zawsze.
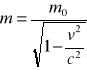
Jest to jedna z najważniejszych zasad obowiązujących w przyrodzie. została uogólniona przez Alberta Einsteina, który wprowadzając równoważność masy i energii połączył klasyczną zasadę zachowania energii z zasadą zachowania masy. Einstein określił masę jako wielkość zależną od prędkości.
m0 - masa spoczynkowa ciała
v - prędkość ciała
c - prędkość światła 3⋅108 m/s
![]()
Zasada równoważności masy i energii mówi, że każda ilość dowolnego rodzaju energii dostarczona ciału powoduje zwiększenie jego masy
![]()
Postać uogólnionej zasady zachowania energii:
![]()
- całkowita energia spoczynkowa
![]()
- suma wszystkich innych rodzajów energii
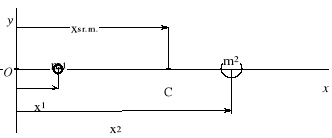
VI. Środek masy.
Punkty materialne to cząstki bezwymiarowe obdarzone masą. Ruch jednego punktu odzwierciedla ruch całego ciała. Środek masy to punkt ciała, który porusza się w taki sam sposób, w jaki poruszałby się pojedynczy punkt materialny poddany tym samym siłom zewnętrznym. Ruch środka masy ciała jest zwany ruchem postępowym tego ciała.
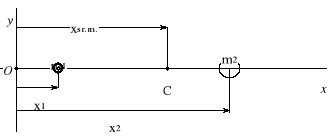
Środek masy dwóch mas m1 i m2 leży na prostej łączącej m1 i m2 w punkcie C, w odległości xśr.m. od początku układu.
![]()
![]()
![]()
Całkowita masa układu:
Dla dużej liczby punktów rozrzuconych w przestrzeni środek masy wyznaczają trzy współrzędne:
![]()
(zapis skalarny)
lub w zapisie wektorowym:
![]()
gdzie: ri - wektor położenia w układzie odniesienia
![]()
rśr.m. - wektor położenia środka masy
![]()
Środek masy układu punktów materialnych zależy tylko od mas tych punktów i od ich wzajemnego rozmieszczenia.
![]()
Jeżeli sumowanie zastąpimy przez całkowanie, to . Dla rśr.m.= 0 (środek masy w początku układu odniesienia) całka ∫ rdm = 0. Ta całka i odpowiadająca jej suma nazywana jest pierwszym momentem masy układu.
VII. Ruch środka masy.
Iloczyn całkowitej masy układu punktów materialnych przez przyspieszenie jego środka masy równa się sumie wektorowej wszystkich sił działających na układ. Maśr.m. = F1 + F2 + ... + Fn
Jeżeli pominiemy siły wewnętrzne działające między punktami materialnymi (zgodnie z III zasadą Newtona siły te będą się znosić), to będą działać tylko siły zewnętrzne i równanie uprości się:
Maśr.m. = Fzew.
Środek masy układu punktów porusza się w taki sposób, jakby cała masa układu była skupiona w środku i jakby wszystkie siły zewnętrzne nań działały.
VIII. Pęd punktu materialnego.
Pędem punktu materialnego nazywamy wektor p zdefiniowany jako iloczyn jego masy m oraz prędkości v, czyli p = mv Pęd jest wielkością wektorową.
![]()
Obecnie II zasada Newtona brzmi: Zmiana pędu ciała w jednostce czasu jest proporcjonalna do wypadkowej siły działającej na to ciało i jest skierowana zgodnie z tą siłą.
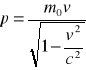
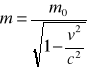
W teorii względności, dla pojedynczego punktu materialnego, druga zasada dynamiki w postaci F = ma jest nieprawdziwa. Jednak w postaci F = dp/dt nadal obowiązuje, jeżeli pęd punktu materialnego zdefiniujemy nie jako m0v, lecz jako , a z tego definicja masy:
Całkowity pęd P jest sumą geometryczną pędów poszczególnych punktów materialnych w tym samym układzie odniesienia: P = p1 + p2 + ... + pn = m1v1 + m2v2 + ... + mnvn
Całkowity pęd układu punktów materialnych jest równy iloczynowi całkowitej masy układu i prędkości jego środka masy.
![]()
IX. Zasada zachowania pędu.
Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru, wtedy całkowity wektor pędu pozostaje stały.
Całkowity pęd układu może być zmieniony tylko przez siły zewnętrzne działające na ten układ.
Pędy poszczególnych punktów układu mogą ulegać zmianom, ale suma tych pędów, jeżeli na układ nie działa żadna wypadkowa siła zewnętrzna, jest stała.
X. Zderzenia.
Siły, które działają przez czas krótki w porównaniu z czasem obserwacji układu, nazywamy siłami impulsowymi (zderzeniowymi) np. podczas uderzenia kijem w piłkę.
Cechy zderzenia:
- możemy wyraźnie rozróżnić czas „przed zderzeniem” i „po zderzeniu”
- prawa zachowania - pędu i energii - pozwalają zdobyć wiele informacji o procesach, które zaszły przed i po zderzeniu, niewiele wiedząc o siłach działających podczas zderzenia
Pęd i popęd.
Zmiana pędu ciała podczas zderzenia:
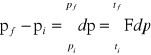
i - początkowy
f - końcowy
Całka siły w przedziale czasu, w którym działa siła, nazywamy popędem siły J. Zmiana pędu ciała pod wpływem działającej siły jest równa popędowi siły.
Zasada zachowania pędu podczas zderzeń.
Jeżeli nie występują siły zewnętrzne, to całkowity pęd układu nie ulega zmianie podczas zderzenia. Siły impulsowe działające podczas zderzenia są siłami wewnętrznymi, które nie mają wpływu na całkowity pęd układu.
Możemy stosować zasadę zachowania pędu podczas zderzeń, jeżeli czas zderzenia jest dostatecznie krótki.
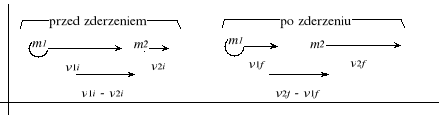
Zderzenia w przestrzeni jednowymiarowej.
Zderzenie nazywamy sprężystym, gdy energia kinetyczna jest w zderzeniu zachowana. Kiedy energia nie jest zachowana, to jest to zderzenie niesprężyste. Kiedy dwa ciała po zderzeniu łączą się ze sobą, to jest to zderzenie całkowicie niesprężyste.
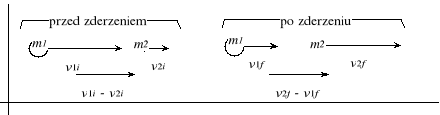
Korzystając z zasady zachowania pędu i zasady zachowania energii:
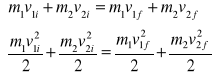
obliczamy: v1i − v2i = v2f − v1f
W zderzeniu sprężystym zachodzącym w przestrzeni jednowymiarowej względna prędkość zbliżania się cząstek przed zderzeniem jest równa względnej prędkości oddalania się cząstek po zderzeniu.
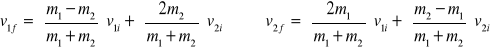
Możemy obliczyć:
Szczególne przypadki:
1 - gdy m1 = m2, to v1f = v2i oraz v2f = v1i . ⇒ W przestrzenie jednowymiarowej, przy sprężystym zderzeniu dwóch cząstek o równych masach, cząstki wymieniają prędkości podczas zderzenia.
2 - cząstka o masie m2 początkowo spoczywa (v2i = 0)
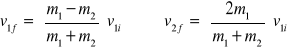
gdy m1 = m2, to v1f = 0, v2f = v1i
gdy m2 jest dużo większe niż m1, to v1f ≅ −v1i oraz v2f ≅ 0
gdy m2 jest dużo mniejsze niż m1, to v1f ≅ v1i oraz v2f ≅ 2 v1i
Przy zderzeniach niesprężystych energia kinetyczna nie jest zachowana. Końcowa energia kinetyczna może być mniejsza niż początkowa, a różnica tych energii przechodzi w ciepło lub w energię potencjalną ciała zdeformowanego podczas zderzenia.
![]()
Podczas zderzenia niesprężystego dwie cząstki pozostają po zetknięciu ze sobą, uzyskując końcową wspólną prędkość vf.
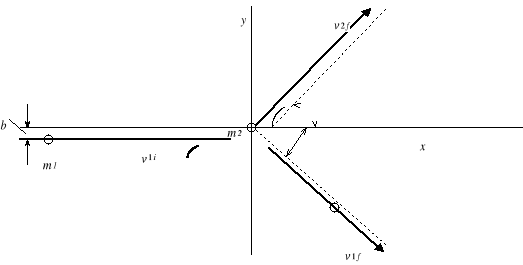
Zderzenia w przestrzeni dwu- i trójwymiarowej.
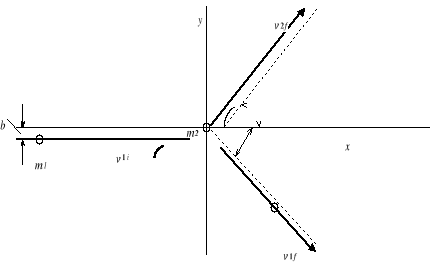
![]()
![]()
Dwie cząstki m1 i m2 ulegają zderzeniu. Początkowo m2 spoczywa (cząstka-tarcza). Odległość b między pierwotnym kierunkiem ruchu cząstki a środkiem tarczy nazywamy parametrem zderzenia. Jest to miara bezpośrednia zderzenia. Gdy b = 0, to zderzenie jest czołowe.
Możemy ułożyć trzy niezależne równania:

- dla składowej x
- dla składowej y
- z zasady zachowania energii
Ruch po zderzeniu możemy opisać tylko wtedy, gdy znamy jedną z wielkości po zderzeniu - v1f, v2f, α1 lub α2.
1
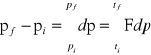
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
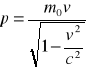
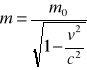
![]()
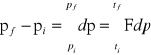
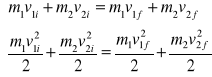
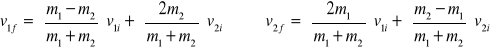
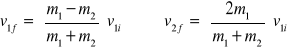
![]()
![]()
![]()
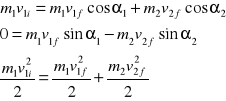
Wyszukiwarka
Podobne podstrony:
LABORKA2, Biotechnologia, Fizyka, Labolatorium
LEPKOŚĆmm, Biotechnologia, Fizyka, Labolatorium
Fizyka - Ćw 60, Biotechnologia, Fizyka, Labolatorium
Fizyka - sprawozdanie 49, Biotechnologia, Fizyka, Labolatorium
neonówka, Biotechnologia, Fizyka, Labolatorium
Elektronika, Biotechnologia, Fizyka, Labolatorium
szeregowy rezonans napiŕciowy, Biotechnologia, Fizyka, Labolatorium
LAB110, Biotechnologia, Fizyka, Labolatorium
ĆWICZENIE NR 2A, Biotechnologia, Fizyka, Labolatorium
2a, Biotechnologia, Fizyka, Labolatorium
Fizyka - sprawozdanie 50, Biotechnologia, Fizyka, Labolatorium
Pojęcia w formacie ściągi, Biotechnologia, Fizyka, Labolatorium
drg, Biotechnologia, Fizyka, Labolatorium
więcej podobnych podstron