Politechnika Łódzka

Filia w Bielsku-Białej

Wydział Budowy Maszyn

Informatyka

Rok 1, Semestr 2

Grupa 2

ĆWICZENIE 66

Temat: Wyznaczanie stałej Plancka

Wykonali:

Korpiela Krzysztof

Krzepis Patryk

Luber Damian

W 1900 roku Max Planck przedstawił teorię, wg której promieniowanie elektromagnetyczne nie jest emitowane w sposób ciągły, ale w postaci ściśle określonych porcji energii, które nazwał kwantami. Energia kwantu jest wprost proporcjonalna do częstotliwości emitowanego promieniowania.

E=h⋅ν

h-stała Plancka; h=6,6249⋅10^-34 [J⋅s]

Energia kwantu promieniowania elektromagnetycznego wyrażana jest zazwyczaj nie w dżulach, ale w elektronowoltach.

Einstein wykorzystując pojęcie kwantu energii promieniowania elektromagnetycznego, wprowadził postulat zgodnie z którym energia fali świetlnej przenoszona jest w postaci oddzielnych kwantów energii, tzw. fotonów, oraz że w wyniku oddziaływania z elektronem, foton przekazuje elektronowi całą swoją energię. Wynikiem czego pomiędzy energią padającego fotonu a maksymalną energią kinetyczną fotoelktronów otrzymuje się prostą zależność, zwaną równaniem Einsteina-Milikana:

hν = W +E_kmax (1)

gdzie:

W - bariera potencjału którą elektron musi pokonać aby opuścić powierzchnię danego materiału, czyli praca wyjścia elektronu z danego materiału.

Jeżeli energia wiązania elektronu W równa pracy, jaką należy wykonać, aby wyrwać elektron z powierzchni płytki (tzw. praca wyjścia), jest większa od energii fotonu to zjawisko nie zajdzie. Zatem praca wyjścia jest równa energii fotonów światła o częstości równej częstości granicznej:

W = hν_g

Wykorzystując równanie Einsteina-Millikana można wyznaczyć stałą Plancka:

h⋅ν=W+E_kmax

Wnioskujemy więc, że stała Plancka określa stosunek energii fotonu światła do częstości fali świetlnej padającej na metal; wielkość tą określamy wzorem h = E_f/ν.

Do wyznaczenia stałej Plancka wykorzystamy zjawisko fotoelektryczne zewnętrzne, polegające na emisji elektronów z metalu pod wpływem padającego światła.

Źródłem światła monochromatycznego (Z) oświetlamy katodę (K) z której emitowane są elektrony. Pomiędzy fotokatodę i anodę przykładamy napięcie hamujące. Woltomierz mierzy napięcie hamujące natomiast amperomierz mierzy prąd anodowy. Maksymalna energia kinetyczna E_kmax=e⋅U_hm, gdzie e-ładunek elektronu; e=1,6⋅10^-19 C, natomiast przez U₀ oznaczymy wartość napięcia hamującego, przy którym prąd anodowy jest równy 0.

Podstawiając e⋅U za E_kmax do równania Einsteina-Millikana otrzymujemy, że:

U_hm= (h/e)⋅ν - (W/e)

Wykres napięcia hamującego U₀ w funkcji częstotliwości ν jest funkcją liniową y=ax+b o współczynnikach a=h/e; b=-W/e. Znając a i b możemy wyznaczyć stałą Plancka oraz pracę wyjścia elektronu z metalu.

Przebieg ćwiczenia

Wykorzystując instalację przedstawioną na schemacie wykonano następujące czynności:

• pomiary dla zależności I_f(ν). Ustawiając kolejno długości fali począwszy od 400 nm, co 20 nm, odczytano na woltomierzu U_R wartości które wpisano do tabeli I(doświadczenie wykonano dwukrotnie). Mając obliczone wartości ν ze wzoru ν=c/λ[1/s=Hz] i korzystając z prawa Ohma obliczono odpowiednio wartości I_f w nA (według zależności U_R/2,49⋅10³),

• pomiary dla zalażności I_f(U_h). Zgodnie z zaleceniem wykonano pomiaru jedynie dla wartości długości fali λ = 500. Zbadano wartości napięcia U_R przy włączonym woltomierzu cyfrowym, mierzącym U_h, nastawiając napięcie hamowania na 0,1 V i kolejne wartości z postępem 0,1 V. Przy wartości 0,662 uzyskano spadek napięcia U_R do zera. Ostatecznie korzystając ponownie z prawa Ohma obliczono wartości I_f w nA (według zależności U_R/2,49). Wyniki pomiaru zostały przedstawione w tabeli nr II,

• pomiary dla zależności U_hm(ν). Ze wzoru podanego wyżej obliczono częstotliwości ν dla poszczególnych długości fali. Pomiary rozpoczęto od λ = 600 nm. Zwiększano U_hm aż do momentu gdy U_R osiągnęło zero, po czym zmniejszano długość fali o 20 nm i powtarzano doświadczenie kończąc na długości fali 400 nm; wyniki pomiarów przedstawia tabela III.

Tab. I.

λ	nm	400	420	440	460	480	500	520	540	560	580	600	620	640	660
UR	V	0,596	0,739	0,848	0,925	0,952	0,954	0,915	0,819	0,698	0,569	0,319	0,095	0,030	0,011
ν	10^15Hz	0,750	0,714	0,682	0,652	0,625	0,60	0,577	0,556	0,536	0,517	0,500	0,484	0,469	0,455
If	nA	239,357	296,787	340,562	371,486	382,329	383,133	367,470	328,916	280,321	228,514	128,112	38,153	12,048	4,418

Tab. II.

λ = 500 nm
Uh	UR	If
V	MV	NA
0.1	617	247,79
0.2	358	143,78
0.3	179	71,89
0.4	72	28,92
0.5	23	9,24
0.6	5	2,01
0.662	0	0,0

Tab.III.

λ	nm	400	420	440	460	480	500	520	540	560	580	600
ν	10^17Hz	0,0075	0,0071	0,0068	0,0065	0,0063	0,0060	0,0058	0,0056	0,0054	0,0052	0,0050
Uhm	V	1,125	1,003	0,898	0,807	0,728	0,660	0,603	0,554	0,513	0,477	0,437
ν1 = [10^17Hz]			U1 = [V]			ν2 = [10^17Hz]			U2 = [V]

Tab. IV.

a ± Δa	B ± Δb	λg1	λg	h ± Δh	W ± ΔW
[10^-15V*s]	[V]	[nm]	[nm]	[J s]	[eV]
2,726 ± 0,082	-0,952 ± 0,021	492,8	0,003	(4,367 ± 0,131)*10^-34	(1,525 ± 0,034)*10^-19

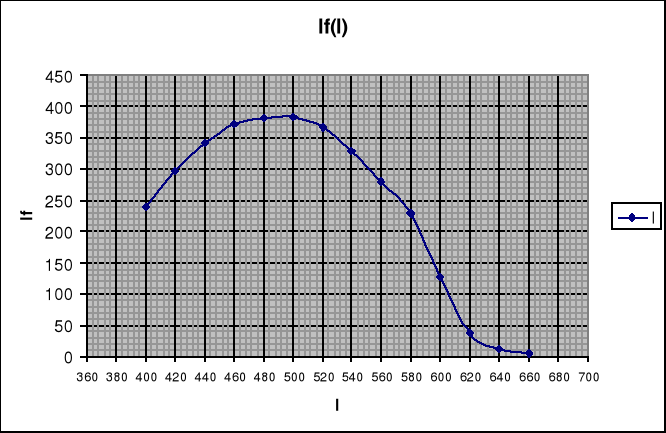
Wykres zależności prądu fotoelektrycznego od częstości fali padającego światła I_f = I_f(λ) przedstawia się następująco:

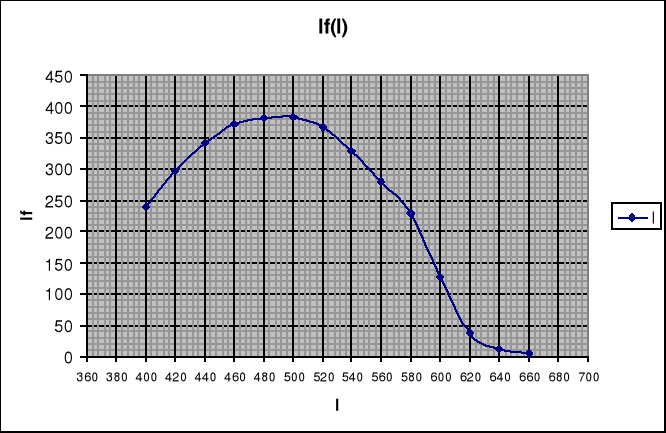
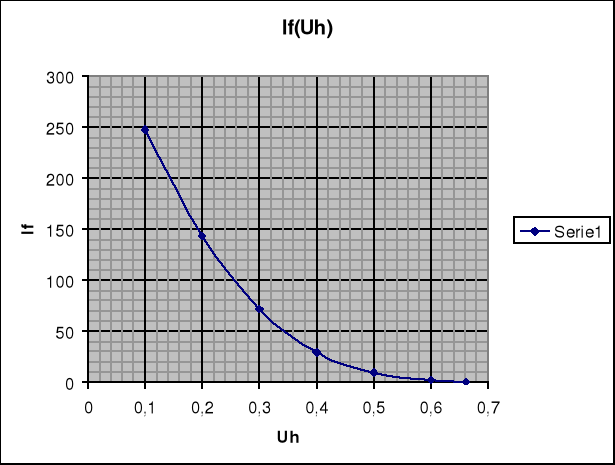
Krzywe hamowania I_f = I_f(U_h) wyznaczone na podstawie pomiarów z Tab. 2 przedstawia poniższy wykres:

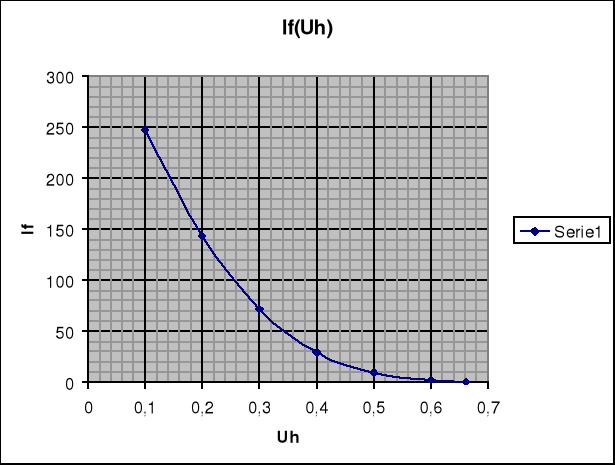
Parametry prostej regresji wyznaczone zostały za pomocą arkusza kalkulacyjnego Quatro Pro dostępnego w pracowni.

a = 272,6⋅10^-17 [V⋅s] b = -0,952 [V]

Δa = 8,2⋅10^-17 [V⋅s] Δb=0,021 [V]

Jednostka została przeliczona z zależności:

a = [V/Hz] = [V/1/s] = [V⋅s]

Wnioski końcowe

Po wyznaczeniu współczynników prostej regresji wykresu U_hm(ν): a i b, jesteśmy w stanie wyznaczyć stałą Plancka h oraz pracę wyjścia elektronu z metalu W.

Korzystając ze wzorów h=e⋅a; W=-e⋅b wyznaczamy kolejno:

Doświadczalną wartość stałej Plancka:

h = 1,602⋅10^-19[C] ⋅ 2,726⋅10^-15[V⋅s] = 4,367⋅10^-34[J⋅s]

Błąd bezwzględny Δh:

Δh = 1,602⋅10^-19[C] ⋅ 0,082⋅10^-15[V⋅s] = 0,131⋅10^-34[J⋅s]

Doświadczalną wartość stałej pracy wyjścia elektronu z metalu:

W = -(1,602⋅10^-19[C] ⋅ (-0,952) [V]) = 1,525⋅10^-19[J]

Błąd bezwzględny ΔW:

ΔW = -(1,602⋅10^-19[C] ⋅ (-0,021) [V]) = 0,034⋅10^-19[J]

Ostatecznie:

h = (4,367 ± 0,131)⋅10^-34 [J⋅s]

W = (1,525 ± 0,034)⋅10^-19 [J]

Na błąd obliczeń wpłynęła niedokładność urządzeń pomiarowych, oraz w pewnym stopniu rozbieżności pomiędzy kilkakrotnie wykonanymi pomiarami, które wymagały uśrednienia (czego prawdopodobnymi przyczynami było opóźnienie wskazania woltomierzy względem zmiany długości fali).

ĆWICZENIE NR 66 WYZNACZANIE STAŁEJ PLANCKA

---