ĆWICZENIE NR 30
WYZNACZANIE WSPÓŁCZYNNIKA ROZSZERZALNOŚCI LINIOWEJ CIAŁ STAŁYCH
WSTĘP TEORETYCZNY
- BUDOWA CIAŁ STAŁYCH, RODZAJE SIŁ WIĄŻĄCYCH ATOMY I CZĄSTECZKI
Charakterystyczną cechą ciał stałych jest sprężystość postaci, prawidłowa budowa wewnętrzna oraz związany z nią kształt geometryczny. Ciała stałe mają budowę o strukturze ziarnistej i elementami ich struktury są atomy, cząsteczki i jony. Razem tworzą one uporządkowane struktury przestrzenne zwane KRYSZTAŁAMI.
W krystalicznym ciele stałym cząstki umieszczone w ściśle określonych punktach przestrzeni, zwanych węzłami sieci przestrzennej, podlegają tylko nieznacznym ruchom drgającym. Monokryształy to duże pojedyncze kryształy o symetrycznych kształtach z zarysowanymi krawędziami i kątami, wykazujące różne właściwości fizyczne (np. łupliwość, rozszerzalność cieplna, współczynnik załamania światła, przewodnictwo elektryczne, itp.) od wyboru kierunku w obrębie danego monokryształu. Zjawisko to nosi nazwę ANIZOTROPII.
Większość ciał stałych w normalnych warunkach nie tworzy jednak monokryształów, jak bowiem wykazały badania mikroskopowe, są one zbudowane z bardzo maleńkich kryształków tworzących tzw. Struktury polikrystaliczne, o dowolnie zorientowanych osiach symetrii, a więc nie wykazują one zjawiska anizotropii, noszą nazwę ciał IZOTROPOWYCH, gdyż mają takie same właściwości fizyczne we wszystkich kierunkach (optyczne, elektryczne, mechaniczne).
Atomy w ciele stałym znajdują się w regularnych od siebie odstępach i utrzymywane są siłami pochodzenia elektrycznego (siły oddziaływania międzycząsteczkowego). Zatem możemy tu zaobserwować istnienie zarówno sił odpychania jak i przyciągania, wartości obu rodzajów sił zależą od odległości między cząsteczkami ciała stałego.
- PODSTAWOWE SIŁY WIĄŻĄCE ATOMY I CZĄSTECZKI CIAŁ STAŁYCH
- wiązania jonowe - powstają wskutek elektrostatycznego przyciągania się różnoimiennych jonów; węzły sieci w kryształach jonowych są obsadzone jonami dodatnimi i ujemnymi i mają wysoką energię sieci krystalicznej (np. NaCl, CaF2, BiF3).
- wiązania kowalencyjne - powstają przy udziale wspólnej pary elektronowej; kryształy kowalencyjne mają zwykle niższą niż jonowe temperaturę topnienia, nie rozpuszczają się w wodzie, są złymi przewodnikami elektryczności (np. diament).
- wiązania metaliczne - elektrony mogą poruszać się swobodnie wokół „zrębów” dodatnich tworząc tzw. gaz elektronowy
- wiązania van der Waalsa - polega na oddziaływaniu dipoli trwałych, dipoli indukowanych lub elektronów w ruchu (siły dyspersyjne), większość związków organicznych, zestalone substancje proste i związki organiczne będące w warunkach normalnych gazami lub cieczami (CH4, Cl2, HCl) mogą w pewnych warunkach tworzyć wskutek słabych oddziaływań krystaliczne sieci cząsteczkowe. Związki te mają niskie temperatury topnienia, małą twardość, nie przewodzą prądu elektrycznego.
- DRGANIA CZĄSTEK W SIECI KRYSTALICZNEJ
Cząstki umieszczone w węzłach sieci krystalicznej podlegają jedynie nieznacznym drganiom
Ruch drgający to ruch okresowy punktu materialnego (tam i z powrotem) po tej samej drodze.
Drgania, w których przyspieszenie cząstki drgającej jest proporcjonalne do wychylenia i ma znak przeciwny, to drgania HARMONICZNE. Wówczas położenia równowagi drgających atomów przesuwają się na nowe, zwiększone odległości. Jednakże cząstki umieszczone w węzłach sieci krystalicznej podlegają jedynie nieznacznym drganiom.
- ZALEŻNOŚC ŚREDNIEJ ODLEGŁOŚCI CZĄSTECZEK OD TEMPERATURY
Ciała stałe przy ogrzewaniu rozszerzają się, ich wymiary (odległości między cząsteczkami) wzrastają wraz ze wzrostem temperatury, co jest powodowane wzmożeniem ruchów drgających atomów i cząsteczek przy ogrzewaniu.
Rozszerzalność ciał to zjawisko fizyczne powodujące zmianę objętości ciała pod wpływem czynników zewnętrznych.
- WSPÓŁCZYNNIK ROZSZERZALNOŚCI LINIOWEJ DLA CIAŁ STAŁYCH
Pojęcie współczynnika rozszerzalności liniowej dla ciał stałych wprowadzono w celu ilościowego ujęcia zjawiska rozszerzalności cieplnej, gdyż dostrzegalne rozszerzenie ciał stałych (o kształcie prętów) zachodzi w głównej mierze w kierunku długości.
α - współczynnik rozszerzalności liniowej
l0 - długość początkowa pręta (ciała stałego)
Δl - przyrost długości pod wpływem wzrostu temperatury
Δt - przyrost temperatury
- WSPÓŁCZYNNIK ROZSZERZALNOŚCI OBJĘTOŚCIOWEJ DLA CIAŁ STAŁYCH
Współczynnik rozszerzalności objętościowej definiujemy jako względny przyrost objętości ciała przypadający na jednostkowy przyrost jego temperatury.
![]()
β - współczynnik rozszerzalności objętościowej
V - objętość początkowa
ΔV - przyrost objętości pod wpływem wzrostu temp.
ΔT - przyrost temperatury
β = 3α → dla ciał izotropowych
β = α1+ α2 + α3 → dla ciał anizotropowych
Wartość współczynnika rozszerzalności liniowej i objętościowej (dla cieczy) jest funkcją temperatury i zwykle z nią rośnie.
- OPIS ĆWICZENIA
1) Należy zmierzyć wielokrotnie długości początkowe l0 przy pomocy przymiaru.
2) Zamontować 3 czujniki zegarowe
3) Po ustablizowaniu się temperatury (przy włączonym ultratermostacie) odczytać temperaturę początkową t0
4) Odczytać na czujnikach zegarowych położenie początkowe
5) Nastawić na termometrze kontaktowym temp o ok. 5° C wyższą. Po ustabilizowaniu się temp. odczytać jej wartość i położenie czujników (przyrost długości Δl).Pomiary prowadzić do maksymalnej temperatury 85° C.
(W praktyce nieco uproszczono cały proces a mianowicie:
- Czujniki zostały wyzerowane w temperaturze t0
- Ze względu na brak czasu (awaria ultratermostat) temperatura podnosiła się stale (do 85° C) a odczyt ze wskazań był niejako w „locie” tj. w momencie gdy na termometrze uchwycona została temperatura (np. 25,30,35,40,45,..° C) zapisywane były wychylenia czujników bez oczekiwania na ustabilizowanie się ultratermostatu.
OBLICZENIA
Współczynnik rozszerzalności liniowej oblicza się ze wzoru:
[1/°]
δl - przyrost długości rurki
δt- przyrost temperatury
l0 - długość początkowa
- nachylenie krzywej rozszerzalności
L.P. |
Temperatura [C°] |
δt [C°] |
0 |
20 |
0 |
1 |
30 |
10 |
2 |
35 |
15 |
3 |
40 |
20 |
4 |
45 |
25 |
5 |
50 |
30 |
6 |
55 |
35 |
7 |
60 |
40 |
8 |
65 |
45 |
9 |
70 |
50 |
10 |
75 |
55 |
[°]
[mm] =2⋅10-5 [m]
Długość początkowa próbek:
- stal 0.815 m
- miedź 0.813 m
- mosiądz 0.814 m
L.P. |
STAL [m] |
MIEDŹ [m] |
MOSIĄDZ [m] |
TEMP. [C°] |
δt [C°] |
0 |
0 |
0 |
0 |
20 |
0 |
1 |
0.000075 |
0.00008 |
0.00008 |
30 |
10 |
2 |
0.00014 |
0.000145 |
0.00016 |
35 |
15 |
3 |
0.000215 |
0.000215 |
0.000235 |
40 |
20 |
4 |
0.00029 |
0.00029 |
0.00032 |
45 |
25 |
5 |
0.000345 |
0.00035 |
0.00039 |
50 |
30 |
6 |
0.000445 |
0.000418 |
0.000465 |
55 |
35 |
7 |
0.000485 |
0.00049 |
0.000545 |
60 |
40 |
8 |
0.000555 |
0.00056 |
0.000625 |
65 |
45 |
9 |
0.00062 |
0.00063 |
0.0007 |
70 |
50 |
10 |
0.000685 |
0.000695 |
0.00078 |
75 |
55 |
- REGRESJA LINIOWA
Dla każdej z trzech próbek należy przeprowadzić regresję liniową w postaci wykresów
Każdy z wykresów jest określony równaniem y = ax + b, gdzie:
x - przyrost temperatury ΔT,
y - przyrost długości ΔL / L
a i b - współczynniki związane z materiałem, który się rozszerza.
![]()
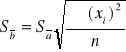
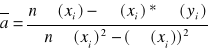
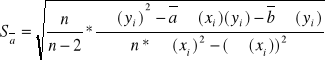
![]()
Podstawowe obliczenia:
Stal [m] ΔL\L (yi) |
Miedź [m] ΔL\L (yi) |
Mosiądz [m] ΔL\L (yi) |
|||
0.0 |
0.0 |
0.0 |
|||
0.000092024 |
0.0000984 |
0.00009828 |
|||
0.000171779 |
0.000178351 |
0.00019656 |
|||
0.000263803 |
0.000264452 |
0.000362407 |
|||
0.000355828 |
0.000356703 |
0.00039312 |
|||
0.000423312 |
0.000430504 |
0.000479115 |
|||
0.000546012 |
0.000514145 |
0.000571253 |
|||
0.000595092 |
0.000602706 |
0.000669533 |
|||
0.000680981 |
0.000688806 |
0.000767813 |
|||
0.000760736 |
0.000774907 |
0.00085995 |
|||
0.000841717 |
0.000854858 |
0.00095823 |
|||
Σ = 0.004731284 |
Σ = 0.004763832 |
Σ = 0.005356261 |
|||
|
Miedź[m]
|
Mosiądz[m]
|
|||
0.0 |
0.0 |
0.0 |
|||
8.4684*10 |
9.6825*10 |
9.6589*10 |
|||
29.508*10 |
31.809*10 |
38.6358*10 |
|||
69.592*10 |
69.9348*10 |
131.3388*10 |
|||
126.6136*10 |
127.237*10 |
154.5439*10 |
|||
179.193*10 |
185.3336*10 |
229.5512*10 |
|||
298.1291*10 |
264.345*10 |
326.3299*10 |
|||
354.1344*10 |
363.2545*10 |
448.2744*10 |
|||
453.7351*10 |
474.4537*10 |
589.5368*10 |
|||
578.7192*10 |
600.4808*10 |
739.514*10 |
|||
708.4878*10 |
730.7822*10 |
918.2047*10 |
|||
Σ = 2806.5806*10 |
Σ = 2857.3131*10 |
Σ = 3585.5884*10 |
|||
Tabela pomocnicza dla obliczeń:
lp. |
Xi |
|
Stal |
Miedz |
Mosiądz |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
10 |
100 |
0.0092024 |
0.000984 |
0.009828 |
3 |
15 |
225 |
0.002576685 |
0.002675265 |
0.0029484 |
4 |
20 |
400 |
0.00527606 |
0.00528904 |
0.00724814 |
5 |
25 |
625 |
0.0088957 |
0.008917575 |
0.017328 |
6 |
30 |
900 |
0.01269936 |
0.01291512 |
0.01437345 |
7 |
35 |
1225 |
0.01911042 |
0.017995075 |
0.019993855 |
8 |
40 |
1600 |
0.02380368 |
0.02410824 |
0.02678132 |
9 |
45 |
2025 |
0.030644145 |
0.03099627 |
0.034551585 |
10 |
50 |
2500 |
0.0380368 |
0.03874535 |
0.0429975 |
11 |
55 |
3025 |
0.046294435 |
0.05270265 |
0.05270265 |
Σ |
Σ = 325 |
Σ =12625 |
Σ = 0.196539685 |
Σ = 0.181692969 |
Σ = 0.197300513 |
PRÓBKA nr 1 (STAL)
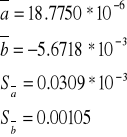
PRÓBKA nr 2 (MIEDŹ)
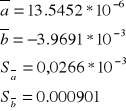
PRÓBKA nr 3 (MOSIĄDZ)
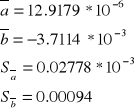
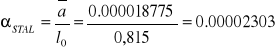
[1/°C]
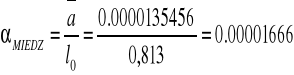
[1/°C]
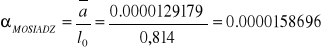
[1/°C]
Dla porównania, wartości tablicowe:
=0.0000115 [1/°C]
=0.0000165 [1/°C]
=0.0000184 [1/°C]
![]()
![]()
![]()
WNIOSKI:
Po przeprowadzeniu pomiarów i obliczeń oraz porównaniu wyników widoczne jest, że niewątpliwie wielkości mierzone w tym ćwiczeniu wymagają ogromnej precyzji i uwagi przy spisywaniu wyników.
Niekompletna precyzja może spowodować, iż otrzymane wyniki mierzonych wielkości będą się różnić od wartości tablicowych.
W wyniku tego powstają błędy pomiarów. Jak widać w końcowych obliczeniach błąd taki powstał, ale jego wartości są naprawdę niewielkie. Przyczyną błędów mogły być w tym przypadku:
błędy powstałe z ciągłego przybliżania wartości w obliczeniach,
dokładność przyrządów,
czynniki zewnętrzne ( lekkie poruszenie próbką lub stołem, na którym znajdowało się całe oprzyrządowanie, powodowało zmiany na czujnikach).
Ogólnie jednak otrzymane wielkości mają wartości podobne do tablicowych, co pozwala stwierdzić, iż całe ćwiczenie zostało sporządzone prawidłowo.
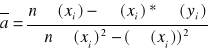
![]()
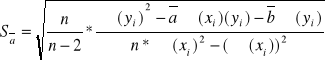
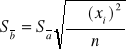
![]()
Wyszukiwarka
Podobne podstrony:
LABORKA2, Biotechnologia, Fizyka, Labolatorium
LEPKOŚĆmm, Biotechnologia, Fizyka, Labolatorium
Fizyka - Ćw 60, Biotechnologia, Fizyka, Labolatorium
Fizyka - sprawozdanie 49, Biotechnologia, Fizyka, Labolatorium
neonówka, Biotechnologia, Fizyka, Labolatorium
Elektronika, Biotechnologia, Fizyka, Labolatorium
szeregowy rezonans napiŕciowy, Biotechnologia, Fizyka, Labolatorium
LAB110, Biotechnologia, Fizyka, Labolatorium
ĆWICZENIE NR 2A, Biotechnologia, Fizyka, Labolatorium
2a, Biotechnologia, Fizyka, Labolatorium
Fizyka - sprawozdanie 50, Biotechnologia, Fizyka, Labolatorium
Pojęcia w formacie ściągi, Biotechnologia, Fizyka, Labolatorium
drg, Biotechnologia, Fizyka, Labolatorium
więcej podobnych podstron