XIV. Hydroliza soli. Sole trudno rozpuszczalne
XIV.1. Hydroliza soli pochodzących od słabych
elektrolitów
Roztwory soli mocnych kwasów i mocnych zasad mają zawsze odczyn obojętny i pH = 7, ponieważ sole te nie ulegają hydrolizie. Hydroliza jest wtórnym procesem decydującym o tym, że roztwory soli słabych zasad i mocnych kwasów mają odczyn kwaśny i pH < 7, natomiast roztwory słabych kwasów i mocnych zasad mają odczyn zasadowy
i pH > 7.
Hydroliza jest reakcją kationów soli słabej zasady lub anionów soli słabego kwasu z wodą. |
Proces hydrolizy soli w roztworach wodnych ma charakter odwracalny i podlega prawu działania mas. Stany równowag w roztworach soli charakteryzują stałe hydrolizy, Kh. Stałych hydrolizy nie podaje się w tablicach!
XIV.1.1. Hydroliza soli słabej zasady (BOH) i mocnego
kwasu (HX)
Typowymi przykładami są sole amonowe: NH4Cl, NH4ClO4, NH4NO3, (NH4)2SO4. Ogólnie sole typu BX.
BX → B+ + X- (dysocjacja)
B+ + H2O ↔ BOH + H+ (hydroliza)

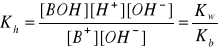
pKh = pKw - pKb
Stopień hydrolizy (β) soli zależy od jej stężenia (cs) w roztworze i wzrasta wraz jego rozcieńczeniem. Świadczy to, że hydroliza soli podlega prawu rozcieńczeń Ostwalda:
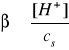
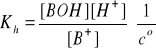
Bilans stężeń w stanie równowagi:
[H+] = [BOH] = β·cs
[B+] = cs - [H+] = cs - β·cs = cs(1- β)
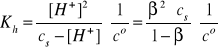
Gdy cs >> [H+], to β << 1, a w konsekwencji mamy:
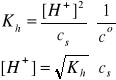
i/lub
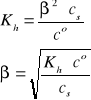
Uwaga: W przypadku (NH4)2SO4, analityczne stężenie kationów NH4+ jest dwukrotnie większe od stężenia tej soli. W roztworze dwóch soli amonowych, np. NH4Cl (cs1) i NH4NO3 (cs2), analityczne stężenie kationów NH4+ jest równe sumie stężeń (cs1 + cs2) obydwu soli.
XIV.1.2. Hydroliza soli słabego kwasu (HA) i mocnej
zasady (MOH)
Typowe przykłady to NaHCOO - mrówczan sodu,
NaCH3COO - octan sodu, KNO2 - azotan(III) potasu,
NaClO - chloran(I) sodu, NaCN - cyjanek sodu. Ogólnie sole typu MA.
MA → M+ + A- (dysocjacja)
A- + H2O ↔ HA + OH- (hydroliza)
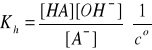

pKh = pKw - pKa
Tak, jak w poprzednim przypadku, hydroliza podlega prawu rozcieńczeń Ostwalda, ponieważ stopień hydrolizy (β) soli zależy od jej stężenia (cs)
w roztworze i wzrasta wraz jego rozcieńczeniem.
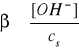
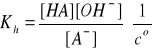
Bilans stężeń w stanie równowagi:
[OH-] = [HA] = β·cs
[A-] = cs - [OH-] = cs - β·cs = cs(1- β)
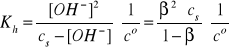
Gdy cs >> [OH-], to β << 1, a w konsekwencji mamy:

i/lub
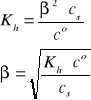
Uwaga: W przypadku soli CaA2, np. octanu wapnia, analityczne stężenie anionów octanowych jest dwukrotnie większe od stężenia tej soli. W roztworze dwóch soli, np. NaNO2 (cs1) i KNO2 (cs2), analityczne stężenie anionów NO2- jest równe sumie stężeń (cs1 + cs2) obydwu soli.
XIV.1.3. Hydroliza soli słabych kwasów i słabych zasad
Typowe przykłady to NH4NO2, NH4CH3COO, NH4CN. Ogólnie sole typu BA. W roztworach tych soli hydrolizuje zarówno kation B+, jak i anion A-.
B+ + H2O ↔ BOH + H+
A- + H2O ↔ HA + OH-
![]()
Stopień hydrolizy soli AB nie zależy od jej stężenia
w roztworze:
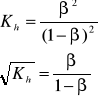
Natomiast odczyn roztworów soli AB zależy od stosunku stałych dysocjacji słabego kwasu HA
i słabej zasady BOH.
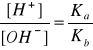
pH - pOH = pKa - pKb,
pH + pOH = pKw,
stąd
pH = (pKw + pKa - pKb)/2.
Przykłady:
1. Obliczyć stopień hydrolizy i pH 0,010 M octanu sodu.
cs = 0,010 mol/dm3, pKa = 4,79, pKw = 14,00
NaCH3COO → Na+ + CH3COO-
CH3COO- + H2O ↔ CH3COOH + OH-
pKh = pKw - pKa = 9,21, Kh = 10-9,21 = 6,17·10-10
![]()
![]()
Założenie: β << 1

Wynik jest poprawny, ponieważ założenie jest spełnione.
[OH-] = β·cs = 2,5·10-6 mol/dm3
pOH = 5,60
pH = 14,00 - 5,60 = 8,40
2. Obliczyć stopień hydrolizy i pH 0,010 M chlorku amonu.
cs = 0,010 mol/dm3, pKb = 4,75, pKw = 14,00
pKh = pKb - pKa = 9,25, Kh = 10-9,25 = 5,62·10-10
NH4Cl → NH4+ + Cl-
NH4+ + H2O ↔ NH4OH + H+
![]()
Założenie: β << 1
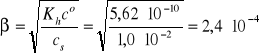
Wynik jest poprawny, ponieważ założenie jest spełnione.
[H+] = β·cs = 2,4·10-6 mol/dm3
pH = 5,62
3. Obliczyć pH roztworu octanu amonu NH4CH3COO.
pKw = 14,00, pKa = 4,79, pKb = 4,75
pH = (pKw + pKa - pKb)/2
pH = (14,00 + 4,79 - 4,75)/2 = 7,02
XIV.2. Sole trudno rozpuszczalne
Oprócz elektrolitów dobrze rozpuszczających się
w wodzie, znamy liczną grupę soli i wodorotlenków metali, których rozpuszczalność w wodzie jest mała lub znikoma. Rozpuszczalność danego związku, rozumiana jako stężenie w roztworze nasyconym, zależy od temperatury.
W porównaniu ze związkami dobrze rozpuszczalnymi, rozpuszczalność (R) - czyli stężenie trudno rozpuszczalnego związku w jego roztworze nasyconym jest znikoma. W każdym przypadku
stały, trudno rozpuszczalny elektrolit, AmBn, nie rozpuszcza się już w jego roztworze nasyconym
w danej temperaturze. Oznacza to, że między tym elektrolitem w fazie stałej i jego roztworem nasyconym ustala się stan równowagi:
AmBn ↔ mAn+ + nBm-
faza stała roztwór nasycony
Stan równowagi w tym układzie determinuje rozpuszczalność R, czyli stężenie związku
w roztworze nasyconym, co wyrażamy za pomocą stałej równowagi zwanej iloczynem rozpuszczalności Ir tego związku. Iloczyn rozpuszczalności związku AmBn jest iloczynem stężeń jonów An+ i Bm- w roztworze nasyconym:
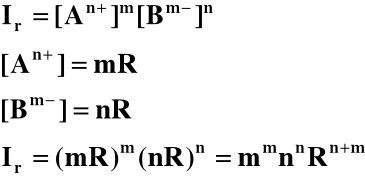
-log Ir = pIr
Jako przykład rozpatrzymy trudno rozpuszczalny
w wodzie fosforan(V) wapnia, Ca3(PO4)2, dla którego mamy:
Ir = (3R)3(2R)2 = 108R5 = 1,0∙10-26
Na tej podstawie możemy obliczyć rozpuszczalność tego związku w wodzie:
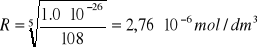
Rozpuszczalność związków trudno rozpuszczalnych, soli lub wodorotlenków, w roztworach elektrolitów różni się od rozpuszczalności tych związków
w czystej wodzie. Przyczyną tego zjawiska są dwa efekty, mianowicie efekt solny i efekt wspólnego jonu.
Efekt solny
Rozpuszczalność trudno rozpuszczalnego związku w roztworach soli nie mającej z nim wspólnego jonu jest zawsze większa od jego rozpuszczalności w czystej wodzie.
Naturę efektu solnego rozpatrzymy na przykładzie chlorku srebra AgCl, którego pIr jest równy 9,75.
AgCl ↔ Ag+ + Cl-
faza stała r-r nasycony
Ir = 10-9,75 = 1,78∙10-10
Gdy chlorek srebra rozpuści się w czystej wodzie, to jego rozpuszczalność jest równa R :
[Ag+] = [Cl-] = R
Ir = [Ag+][Cl-] = R2
R = (Ir)1/2 = 1,33∙10-5 mol/dm3
Natomiast rozpuszczalność R' chlorku srebra
w 0,01 M roztworze KNO3, który nie ma
z chlorkiem srebra wspólnego jonu, jest nieco większa niż w wodzie. Wynika to z faktu, że
w czystej wodzie współczynniki aktywności jonów, yAg+ i yCl-, są równe 1, natomiast w 0,01 M roztworze KNO3 są równe 0,857.
Ir = yAg+·yCl-[Ag+][Cl-] = yAg+·yCl-(R')2
R' = 1,56∙10-5 mol/dm3
Efekt wspólnego jonu
Ponownie rozpatrzymy chlorek srebra. Tym razem postawimy pytanie o jego rozpuszczalność R' w 0,10 M chlorku sodu, NaCl, który z chlorkiem srebra ma wspólny anion. W tym przypadku
w uzyskanym roztworze nasyconym mamy:
[Ag+] = R'
[Cl-] = R' + cNaCl
Ir = R'(R' + cNaCl)
Zakładając, że cNaCl >> R' otrzymujemy
Ir = R' cNaCl
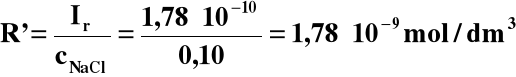
,
co pozostaje w bardzo dobrej zgodności z przyjętym założeniem, ponieważ rozpuszczalność chlorku srebra zmalała około 7500 razy.
Uzyskany wynik upoważnia do ogólnego wniosku, że elektrolity o wspólnym jonie zmniejszają rozpuszczalność trudno rozpuszczalnego związku nawet o kilka rzędów wielkości względem jego rozpuszczalności w czystej wodzie. Potwierdza to również przedstawiony niżej przykład.
Przykład
Porównać rozpuszczalność wodorotlenku Mn(II)
w czystej wodzie i 0,01 M NaOH. pIr Mn(OH)2 jest równy 12,72.
Mn(OH)2 ↔ Mn2+ + 2OH-
faza stała roztwór nasycony
Ir = 10-12,72 = 1,9∙10-13
Rozpuszczalność w czystej wodzie:
[Mn2+] = R, [OH-] = 2R
Ir = R∙(2R)2 = 4R3
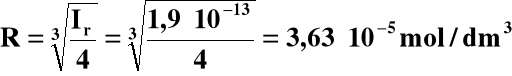
Rozpuszczalność w 0,01 M NaOH:
[Mn2+] = R', [OH-] = 2R' + cNaOH
Ir = R'∙(2R' + cNaOH)
Założenie: cNaOH >> 2R'
Ir = cNaOH∙R'
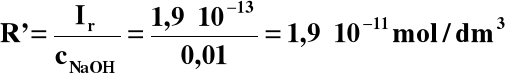
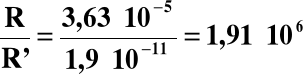
Jak widać, rozpuszczalność Mn(OH)2 w 0,01 M NaOH jest około dwa miliony razy mniejsza od rozpuszczalności w czystej wodzie.
Omawiane na dzisiejszym wykładzie tematy mają ważne znaczenie praktyczne w chemii analitycznej. Hydroliza soli w roztworach wzorcowych, czyli roztworach o ściśle określonym stężeniu jonów danego rodzaju, jest zjawiskiem niepożądanym. Przykładowo, hydroliza roztworów wzorcowych o dokładnie znanym stężeniu kationów Fe3+ prowadzi do wytrącenia się trudno rozpuszczalnego wodorotlenku Fe(OH)3. Z tego powodu roztwory soli Fe(III) zakwasza się kwasem solnym lub siarkowym(VI), co zgodnie z regułą przekory zapobiega reakcji hydrolizy.
Efekt wspólnego jonu na rozpuszczalność związków trudno rozpuszczalnych wykorzystuje się w analizie wagowej (grawimetria) i analizie miareczkowej (precypitometria), ponieważ w obydwu przypadkach pożądana jest jak najmniejsza rozpuszczalność trudno rozpuszczalnego związku, stanowiąca podstawę oznaczeń grawimetrycznych, np. baru jako BaSO4, żelaza jako Fe2O3, lub oznaczeń precypitometrycznych, np. srebra jako AgCl.
Wyszukiwarka
Podobne podstrony:
14 Hydroliza, bufory, sole trudnorozpuszczalne
Slownik ChemLab, Studia, Chemia ogólna wykład
teoria redox ti7, Studia, Chemia ogólna wykład
Iloczyn rozpuszczalności soli trodno rozpuszczalnych, studia, chemia, chemia fizyczna, sprawozdania,
chf wykład 6, Studia, Chemia, fizyczna, wykłady
pytania z examinu, Studia, Chemia, ogólna, examin
chf wykład 3, Studia, Chemia, fizyczna, wykłady
chf wykład 8, Studia, Chemia, fizyczna, wykłady
chf wykład 1, Studia, Chemia, fizyczna, wykłady
sole pojedyncze, ~FARMACJA, I rok, CHEMIA OGÓLNA I NIEORGANICZNA, egzamin sole
chf wykład 5, Studia, Chemia, fizyczna, wykłady
CHEMIA OGÓLNA - wykład 1, studia PWr, Chemia, CHEMIA OGÓLNA
chf wykład 4, Studia, Chemia, fizyczna, wykłady
sole podwójne, ~FARMACJA, I rok, CHEMIA OGÓLNA I NIEORGANICZNA, egzamin sole
więcej podobnych podstron