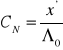Robert Maniura

Sprawozdanie z ćwiczenia nr B-20: Iloczyn rozpuszczalności soli trudno rozpuszczalnych.

2. Wstęp teoretyczny:

W roztworze nasyconym istnienie stan równowagi dynamicznej, gdyż tyle samo jonów przechodzi w jednostce czasu do roztworu, ile ich osadza się na kryształach substancji BA. Szybkość narastania jest wtedy równa szybkości rozpuszczania substancji BA:

po podzieleniu obu stron równania przez
otrzymuje się:

gdzie
oznacza iloczyn rozpuszczalności.

Jest to równanie iloczynu rozpuszczalności soli BA.

Równanie powyższe wyrażone słowami głosi, że w roztworze nasyconym trudno rozpuszczalnej soli iloczyn stężeń jonów, na które ta sól się rozpada, jest w danej temperaturze wielkością stałą. Wielkość ta nazywa się iloczynem rozpuszczalności danej soli.

Należy pamiętać, że iloczyn stężeń jonów, z których składa się dana sól, jest równoznaczny z iloczynem rozpuszczalności tylko w przypadku roztworu nasyconego. Dopóki w jakimś roztworze iloczyn stężeń tych jonów ma wartość mniejszą od iloczynu rozpuszczalności, roztwór jest nienasycony w stosunku do rozpuszczanej soli i wytrącenie osadu jest niemożliwe. Jeśli natomiast iloczyn stężeń jonów przewyższa iloczyn rozpuszczalności, roztwór jest przesycony, a więc znajduje się w równowadze nietrwałej; w pewnych warunkach może nastąpić powrót do stanu równowagi (roztwór nasycony) i związane z tym wydzielanie przez roztwór określonej ilości soli.

Sformułowanie iloczynu rozpuszczalności, podane powyżej jest słuszne tylko w przypadku soli bardzo trudno rozpuszczalnych; w roztworze nasyconym znajduje się wtedy tak mała ilość jonów, że ich aktywności można uważać za równe stężeniom. W bardziej poprawnym, ogólnym ujęciu iloczynu rozpuszczalności jest iloczynem nie stężeń, lecz aktywności:

albo

gdzie
i
oznaczają aktywności poszczególnych jonów,
i
- odpowiednie współczynniki aktywności.

Jak z tego wynika, iloczyn stężeń jonów w roztworze nasyconym elektrolitu nie jest - wbrew teorii klasycznej - wielkością stałą, gdyż jest on odwrotnie proporcjonalny do iloczynu współczynników aktywności:

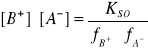
te zaś zależą od siły jonowe roztworu.

Wielkością stałą jest więc iloczyn stężeń jonów tylko w przypadku roztworów nieskończenie rozcieńczonych, dla których siła jonowa równa się zeru, a tym samym współczynniki aktywności równają się jedności. Dla takich roztworów (substancji trudno rozpuszczalnej):

Ilość osadu nie ma wpływu na równowagę jonów w roztworze.

W przypadku trudno rozpuszczalnej soli dysocjującej na więcej niż 2 jony iloczyn rozpuszczalności przybiera postać nieco bardziej złożoną, np. dla Ca(OH)₂:

Ca(OH)₂
Ca²⁺ + 2 OH^- wtedy
gdzie
oznacza stężenie jonów w roztworze nasyconym będących w równowadze z osadem.

Obliczenia teoretyczne, związane z reakcjami wytrącania osadu trudno rozpuszczalnego, a więc np. obliczanie rozpuszczalności substancji, ustalenie warunków wytrącania lub rozpuszczania osadów, mają duże znaczenie w analizie chemicznej zarówno jakościowej, jak i ilościowej. W obliczeniach tych najczęściej nie uwzględnia się siły jonowej roztworu, biorąc pod uwagę tylko stężenia odpowiednich jonów w roztworze nasyconym, w którym znajduje się tak mała ilość jonów, że ich aktywności można uważać za równe stężeniom.

Do obliczenia iloczynu rozpuszczalności badanej substancji konieczna jest znajomość jej rozpuszczalności, którą można wyznaczyć doświadczalnie wykorzystując w tym celu przewodnictwo właściwe i równoważnikowe.

Aby obliczyć stężenia soli trudno rozpuszczalnych wystarczy zmierzyć w ich nasyconych roztworach przewodnictwo właściwe oraz znać wartości tabelaryczne przewodnictwa granicznego równoważnikowego. Do obliczeń możemy posłużyć się przewodnictwem granicznym równoważnikowym danych elektrolitów ponieważ ich stężenia są bardzo małe. Do obliczenia stężenia elektrolitów będę posługiwał się wzorem na przewodnictwo równoważnikowe:

gdzie
oznacza przewodnictwo graniczne równoważnikowe danego elektrolitu (tabelaryczne);
oznacza przewodnictwo właściwe (zmierzone);
oznacza stężenie wyrażone w gramorównoważnikach na jednostkę objętości.

Znając
można obliczyć
(stężenie molowe) z wzoru:

gdzie
oznacza gramorównoważnik danego elektrolitu.

Obliczone
(stężenie molowe) można wykorzystać do obliczenia iloczynu rozpuszczalności wstawiając te stężenie w miejsce
we wzorze na iloczyn rozpuszczalności dla poszczególnych soli:

dla CaSO₄ -

dla PbCl₂ -

dla Ca(OH)₂ -

3. Opracowanie wyników:

Wyznaczam stałą naczyńka.

Stężenie roztworu KCl [mol/l]	Przewodnictwo właściwe (doświadczalne) [S/cm]	Przewodnictwo właściwe (teoretyczne) [S/cm]	Stała naczyńka	Stała naczyńka (wartość średnia)
0,1	0,01733	0,01213	0,699942297	0,656019413
0,01	0,00207	0,001329	0,642028986
0,001	0,00023	0,000144	0,626086957

Obliczam stężenie wyrażone w gramorównoważnikach na jednostkę objętości oraz stężenie molowe dla poszczególnych roztworów nasyconych soli trudno rozpuszczalnych.

Elektrolit	Przewodnictwo właściwe (zmierzone) [S/cm]	Przewodnictwo właściwe (obliczone) [S/cm]	Przewodnictwo graniczne równoważnikowe (tabelaryczne) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]	Stężenie [g-równ/l]	Stężenie molowe [mol/l]	Iloczyn rozpuszczalności (obliczony według powyższych wzorów)
CaSO4	0,0031	0,00203366	0,1395	0,014578209	0,007289105	5,31
PbCl2	0,0065	0,004264126	0,331	0,012882556	0,006441278	1,07
Ca(OH)2	0,0108	0,00708501	0,2581	0,027450638	0,013725319	1,03

Porównanie wartości iloczynów rozpuszczalności obliczowych dla soli z wartościami tablicowymi:

Sól	Iloczyn rozpuszczalności (obliczony)	Iloczyn rozpuszczalności (tablicowy)	Błąd procentowy
CaSO4	5,31	3,1	71,29 %
PbCl2	1,07	1,58	93,23%
Ca(OH)2	1,03	7,59	35,70%

4. Wnioski:

Błędy, które wynikły podczas doświadczenia spowodowane są tym, iż w obliczeniach zastosowane są wartości literaturowe przewodnictwa granicznego równoważnikowego dla roztworów. Doświadczalne wyznaczanie rozpuszczalności substancji trudno rozpuszczalnych nie należy do zadań łatwych, tym też tłumaczy się pewne różnice w wartościach iloczynu rozpuszczalności, podawanych przez różnych badaczy. Ze stałej iloczynu rozpuszczalności można obliczyć stężenie jonów, a więc i rozpuszczalność danego związku.

5. Literatura:

Kazimierz Gumiński „Wykłady z chemii fizycznej”.

Zdzisław Stefan Szmal, Tadeusz Lipiec „Chemia analityczna z elementami analizy instrumentalnej”.

Witold Mizerski „Tablice chemiczne”.

1

---