Sprawozdanie z ćwiczenia nr 19: Ciepło rozpuszczania soli jonowej.
1. Wstęp teoretyczny:
Procesowi rozpuszczania w ciekłych rozpuszczalnikach towarzyszy efekt cieplny, zwany ciepłem rozpuszczania. Obserwowany efekt cieplny związany jest ze zmianą stanu termodynamicznego substancji przy przeniesieniu czystego składnika do roztworu.
W pierwszym etapie ulega zniszczeniu sieć krystaliczna substancji kosztem pobrania ciepła z otoczenia. W drugim etapie cząsteczki te (lub jony) ulegają procesowi solwatacji, czemu towarzyszy wydzielenie się dużej ilości energii (w postaci ciepła) zwanej energią solwatacji (lub hydratacji gdy rozpuszczalnikiem jest woda). Ciepło rozpuszczania jest sumą tych dwóch efektów cieplnych i z tego względu może być zarówno dodatnie jak i ujemne. Zależeć to będzie od wzajemnego stosunku wielkości energii sieciowej do energii solwatacji. Zajmiemy się teraz ilościowym opisem procesu rozpuszczania. W tym celu zauważmy, że w różnych możliwych procesach rozpuszczania, stan początkowy układu jest zawsze taki sam (zwykle jest nim 1 mol czystej substancji w temperaturze 298 K i pod ciśnieniem 1 atm.), natomiast stanów końcowych może być tyle ile jest możliwych końcowych stężeń powstałego w wyniku procesu rozpuszczania roztworu. Zmiany entalpii dla procesu przejścia układu ze wspólnego stanu początkowego do różnych stanów końcowych muszą być oczywiście różne. Z tego względu rozróżniać będziemy dwa ciepła rozpuszczania: integralne i różniczkowe ciepło rozpuszczania.
Niech w procesie rozpuszczania na m (masę w kg) rozpuszczalnika przypada n moli substancji rozpuszczonej; w wyniku procesu rozpuszczania powstanie roztwór o stężeniu molarnym Cm:
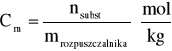
gdzie mrozpuszczalnika jest masą rozpuszczalnika w [kg]; nsubst jest liczbą moli substancji. Niech ciśnienie i temperatura układu będą ustalone. Integralnym ciepłem rozpuszczania (na 1 mol substancji rozpuszczonej) nazywamy efekt cieplny towarzyszący rozpuszczeniu 1 mola substancji rozpuszczonej w takiej ilości rozpuszczalnika, aby w wyniku powstał roztwór o stężeniu molarnym Cm. Ponieważ warunki procesu określiliśmy jako izotermiczno - izobaryczne, zatem ciepło to jest równe zmianie entaplii (Hint).
W termodynamicznej charakterystyce roztworów, duże znaczenie ma tzw. różniczkowe ciepło rozpuszczania. Zauważmy, że integralne ciepło rozpuszczania otrzymujemy jako efekt cieplny procesu, w którym do pewnej masy ciekłego rozpuszczalnika dodajemy 1 mol substancji rozpuszczonej, w wyniku czego powstaje roztwór o stężeniu Cm. Różniczkowe ciepło rozpuszczania definiujemy natomiast jako efekt cieplny towarzyszący rozpuszczaniu 1 mola substancji rozpuszczonej w roztworze o stężeniu Cm, przy czym stężenie tego roztworu nie może ulec zmianie.
2. Opracowanie wyników:
Zmiany temperatury T obliczam z wykorzystaniem równania termistora:
![]()
gdzie: b = 3731,5577![]()
2,7854; lnR∞ = -9,434696![]()
0,009139; z równania tego można obliczyć odpowiednio wszystkie temperatury pomiaru;
T = Tp - Tk gdzie: Tp - temperatura przed rozpoczęciem rozpuszczania soli; Tk - temperatura po zakończeniu procesu rozpuszczania;
Ciepło rozpuszczania wynosi:
Qrozp = -(mrcw + ww) T gdzie: Qrozp - ciepło rozpuszczania; mr - masa roztworu; cw - ciepło właściwe roztworu (4,184 [J/g*K]); ww - wartość wodna kalorymetru (196,24 [J/K]); ciepło właściwe roztworu przyjęto w badanym zakresie za równe ciepłu właściwemu wody.
Integralną entalpię rozpuszczania oblicza się z równania:
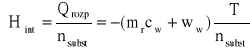
Czas [min] |
Czas [s] |
Pomiar I mCaCl2 = 2,2958 g |
Pomiar II mCaCl2 = 4,0012 g |
Pomiar III mCaCl2 = 7,0011 g |
0 |
0 |
22 |
20,7 |
18,4 |
0,5 |
30 |
22 |
20,7 |
18,4 |
1 |
60 |
22 |
20,7 |
18,4 |
1,5 |
90 |
21,9 |
20,7 |
18,4 |
2 |
120 |
21,9 |
20,7 |
18,4 |
2,5 |
150 |
21,9 |
20,7 |
18,4 |
3 |
180 |
21,8 |
20,6 |
18,4 |
3,5 |
210 |
21,8 |
20,5 |
18,3 |
4 |
240 |
21,7 |
20,4 |
18,2 |
4,5 |
270 |
21,6 |
20,4 |
18,1 |
5 |
300 |
21,6 |
20,3 |
18,1 |
5,5 |
330 |
21,6 |
20,2 |
18 |
6 |
360 |
21,5 |
20,1 |
17,9 |
6,5 |
390 |
21,5 |
20 |
17,9 |
7 |
420 |
21,4 |
20 |
17,9 |
7,5 |
450 |
21,4 |
20 |
17,8 |
8 |
480 |
21,4 |
19,9 |
17,8 |
8,5 |
510 |
21,3 |
19,9 |
17,8 |
9 |
540 |
21,4 |
19,9 |
17,8 |
9,5 |
570 |
21,4 |
19,9 |
17,7 |
10 |
600 |
21,3 |
19,8 |
17,7 |
10,5 |
630 |
21,3 |
19,8 |
17,7 |
11 |
660 |
21,3 |
19,8 |
17,7 |
11,5 |
690 |
21,3 |
19,8 |
17,7 |
12 |
720 |
21,3 |
19,8 |
17,6 |
12,5 |
750 |
21,3 |
19,7 |
17,6 |
13 |
780 |
21,3 |
19,7 |
17,6 |
13,5 |
810 |
21,2 |
19,7 |
17,6 |
14 |
840 |
21,2 |
19,7 |
17,6 |
14,5 |
870 |
21,2 |
19,7 |
17,6 |
15 |
900 |
21,1 |
19,7 |
17,6 |
15,5 |
930 |
21,1 |
19,7 |
17,6 |
Pomiar |
Masa H2O [g] |
Masa soli [g] |
Stężenie molarne Cm [mol/kg] |
T |
Ciepło rozpuszczania Qrozp [J] |
Integralna entalpia rozpuszczania Hint [J/mol] |
||||
1 |
400,0 |
2,2958 |
0,05171373 |
-0,7752 |
1456,96 |
70433,82 |
||||
2 |
|
4,0012 |
0,090128485 |
-1,1939 |
2252,47 |
62479,50 |
||||
3 |
|
7,0011 |
0,157702323 |
-1,0920 |
2073,84 |
32875,87 |
||||
2.4. Obliczenie maksymalnego ciepła rozpuszczania na podstawie wzoru:
![]()
gdzie; T = 0,01 [K]; mr = 0,5 [g]; cw = 4,184 [J/g*K]; mr = 40 [g]; ww = 196,24 [J/K];
![]()
= 2,37 J
3. Wnioski:
Wykres zależności integralnego ciepła rozpuszczania od stężenia charakteryzuje dość dobrze przebieg tego procesu i zbliża się asymptotycznie do osi stężenia wraz ze wzrostem (wykres nie wykonany ponieważ zbyt mało pomiarów o różnych stężeniach). Zniszczenie sieci krystalicznej związane jest zawsze z energią równą energii sieciowej i oczywiście nie zależy od stężenia końcowego. Oznacza to, że hydratacja jonów dająca bardzo duże efekty przy niższych stężeniach, przy wyższych stężeniach CaCl2 się ustala.
3
Wyszukiwarka
Podobne podstrony:
Iloczyn rozpuszczalności soli trodno rozpuszczalnych, studia, chemia, chemia fizyczna, sprawozdania,
HCOOH, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Diagram fazowy Gibbsa, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Entropia mieszania, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Badanie lepkości cieczy metodą Hopplera, studia, chemia, chemia fizyczna, sprawozdania, sprawka
izoterma adsorbcji, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Stała szybkości reakcji jodowania acetonu, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Energia aktywacji przepływu lepkiego, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Kinetyka reakcji elektroutlenienia 1-propanolu, studia, chemia, chemia fizyczna, sprawozdania, spraw
Elektronowe widma absorpcyjne, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Dyspersja współczynnika załamania światła, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Ciepło rozpuszczania soli jonowej
HCl i HJ, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Jonity1, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Izoterma adsorpcji 1, studia, chemia, chemia fizyczna, sprawozdania, sprawka
HCl, studia, chemia, chemia fizyczna, sprawozdania, sprawka
HJ, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Grupy symetrii, studia, chemia, chemia fizyczna, sprawozdania, sprawka
Entalpia parowania, studia, chemia, chemia fizyczna, sprawozdania, sprawka
więcej podobnych podstron