Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
HYDROLIZA, BUFORY,
SOLE
TRUDNOROZPUSZCZALN
E
Powiązanie zjawiska hydrolizy ze słabymi elektrolitami.
Reakcja hydrolizy. Stała hydrolizy i jej wyznaczanie ze
stałej dysocjacji. Definicja roztworu buforowego.
Przykłady buforów kwaśnych i zasadowych. Zakres
buforowania i pojemność buforu. Równowaga w
nasyconych roztworach soli. Iloczyn rozpuszczalności i
jego związek z rozpuszczalnością.
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
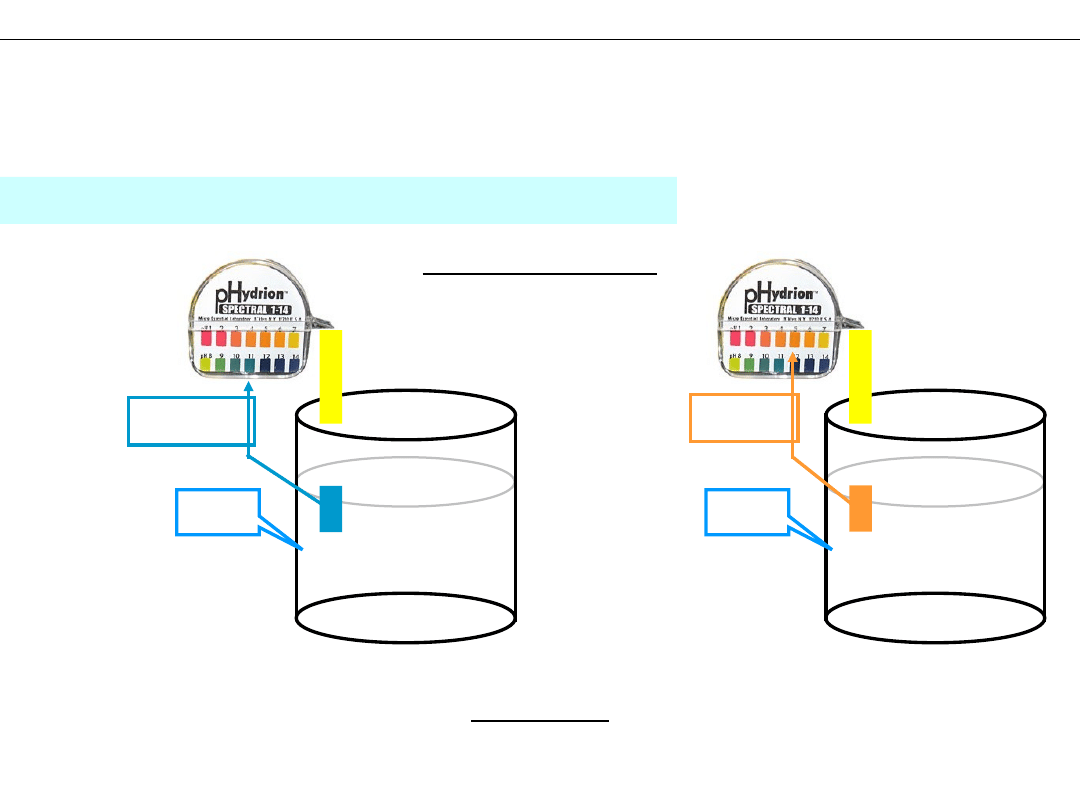
Roztwory niektórych soli mają odczyn kwaśny lub zasadowy.
HYDROLIZA
SOLWOLIZA – reakcja substancji z rozpuszczalnikiem
HYDROLIZA – reakcja substancji z wodą
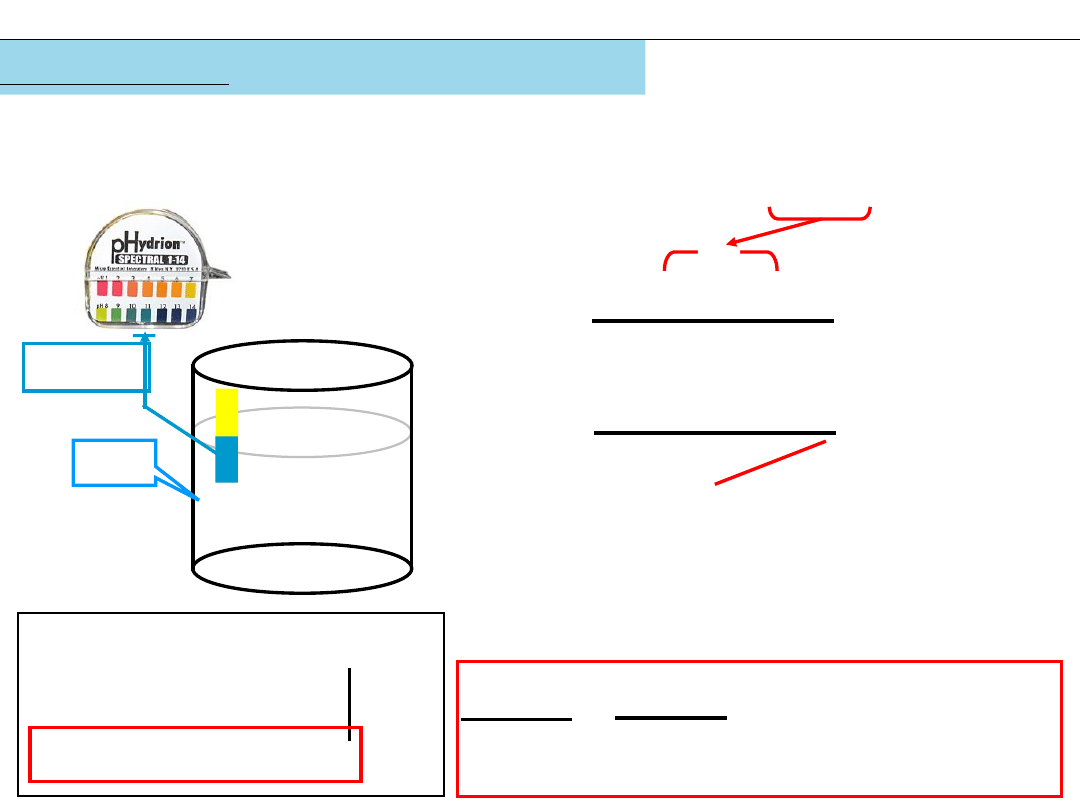
Doświadczenie:
KCN
H
2
O
+
−
NH
4
Cl
H
2
O
+ −
Wniosek:
pH~11
pH~5
HCN H
+
+ CN
−
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
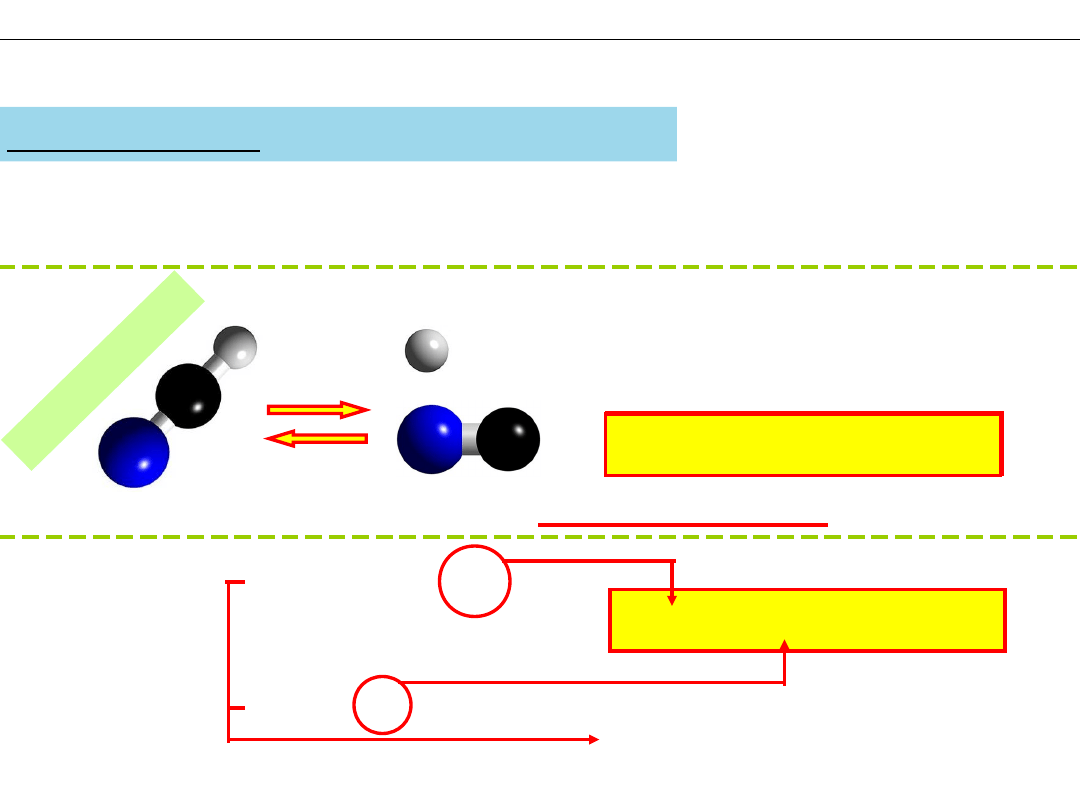
HYDROLIZA
Doświadczenie 1 – zasadowy roztwór
KCN
KCN
jest solą słabego kwasu
HCN
Dlaczego
HCN
jest słabym kwasem?
Wiązanie H−CN jest silne ...
jony H
+
i CN
−
chętnie łączą się
z powrotem w cząsteczki HCN.
HCN H
+
+ CN
−
Reakcja odwracalna - równowagowa
CN
−
+ H
2
O
HCN +
OH
−
H
C
N
−
N
C
H
+
KCN K
+
+ CN
−
H
2
O H
+
+
OH
−
KCN + H
2
O
HCN + KOH
CN
−
+ H
+
HCN
PR
ZY
PO
M
NI
EN
IE
W roztworze:
Autodysocjacja
wody:
?
razem
10
−9
10
−14
[CN
−
] · [H
2
O]
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Doświadczenie 1 – zasadowy roztwór
KCN
CN
−
+ H
2
O
HCN + OH
−
KCN + H
2
O
HCN + KOH
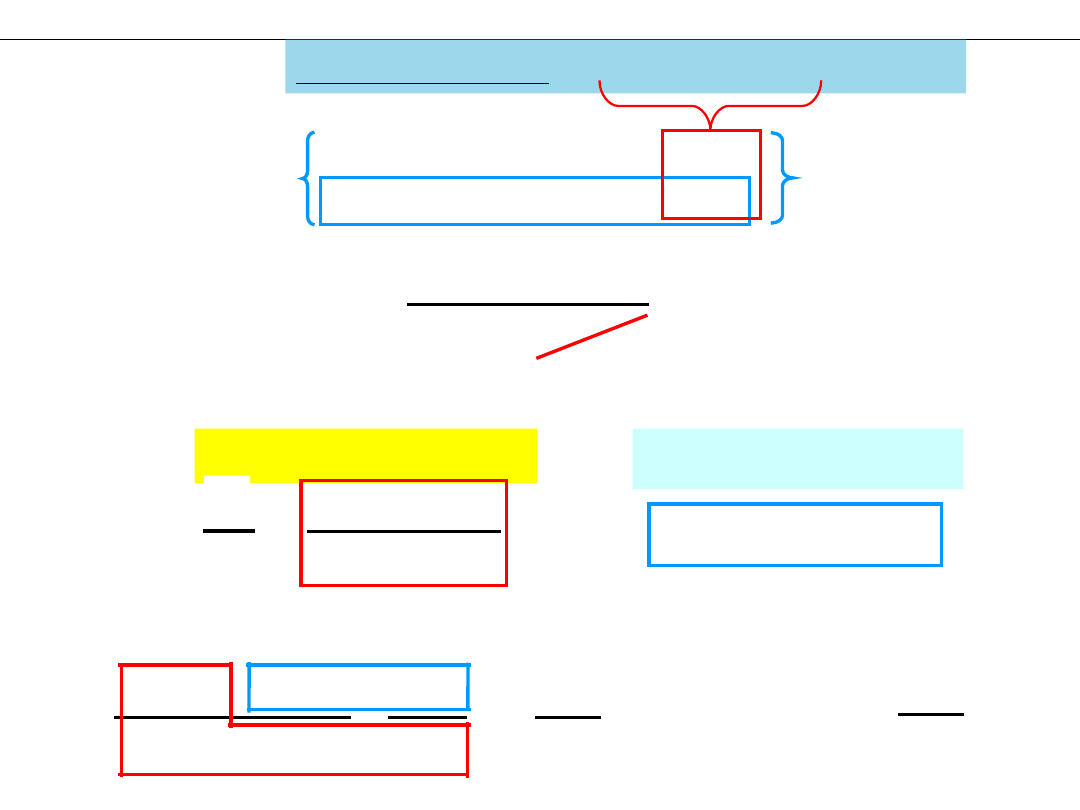
Reakcja
równowagowa
[HCN]
· [OH
−
]
K =
h
wartość stała
Stała
hydrolizy
=
?
(trzeba obliczyć)
Hydroliza wiąże się z dwoma równowagami...
HCN H
+
+ CN
−
H
2
O H
+
+ OH
−
=
[HCN]
[H
+
]
· [CN
−
]
K
w
= [H
+
] · [OH
−
]
... powinien więc istnieć związek pomiędzy
K
h
a
K
a
i
K
w
[HCN]
· [OH
−
]
K =
h
[CN
−
]
·
[H
+
]
[H
+
]
=
K
w
K
a
Dla
CN
−
: Kh =
=10
−5
K
a
1
K
a
Reakcja
HYDROLIZY
jonów
CN
−
(cyjanku potasu)
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Doświadczenie 1 – zasadowy roztwór
KCN
Jakie jest pH roztworu KCN o stężeniu początkowym c
a
= 0,4 M?
Stała
hydrolizy
[CN
−
]
[HCN]
· [OH
−
]
K =
h
= 10
−5
CN
−
+ H
2
O
HCN + OH
−
0,4 – [OH
−
]
[OH
−
]
· [OH
−
]
K =
h
= 10
−5
małe
[OH
−
]
2
= 0,4
·10
-5
= 4 ·10
-6
[OH
−
] = 2 ·10
-3
pOH = 2,7
pH =
K
w
= [H
+
] · [OH
−
]
−log
10
−14
= [H
+
] · [OH
−
]
14 = pH + pOH
=
tyle samo
14 - 2,7 = 11,3
c
a
=
β
– stopień hydrolizy
[HCN]
c
a
[OH
−
]
=
KCN
H
2
O
pH~11
(KCN: 0,002/0,4=0,005)
Wykład 14 –
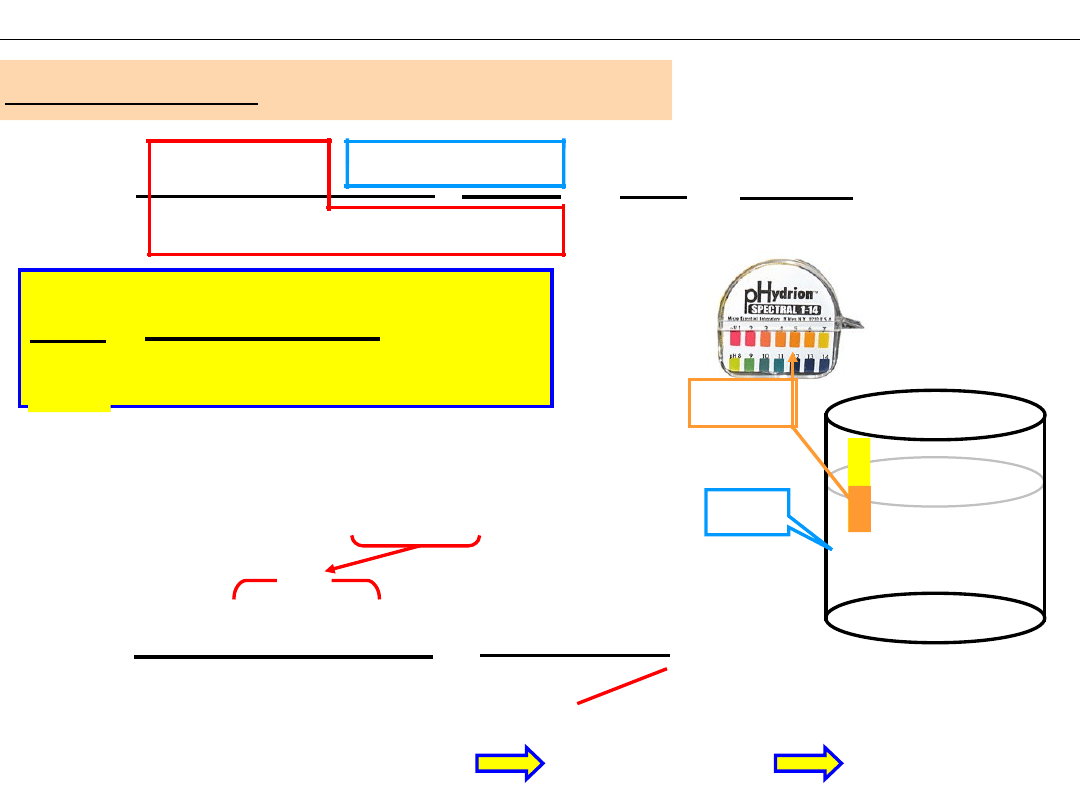
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Doświadczenie 2 – kwaśny roztwór
NH
4
Cl
NH
4
Cl jest solą słabej zasady NH
3
·H
2
O
NH
3
·H
2
O NH
4
+
+ OH
−
NH
3
·H
2
O NH
4
+
+ OH
−
Reakcja odwracalna - równowagowa
NH
4
Cl NH
4
+
+ Cl
−
H
2
O H
+
+ OH
−
NH
4
Cl + H
2
O
NH
3
·H
2
O + HCl
NH
4
+
+ OH
−
NH
3
·H
2
O
W roztworze:
Autodysocjacja
wody:
razem
NH
4
+
+ H
2
O
NH
3
·H
2
O + H
+
[NH
3
·H
2
O] · [H
+
]
[NH
4
+
]
=
K
h
[NH
3
·H
2
O] · [H
+
]
[OH
−
]
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Doświadczenie 2 – kwaśny roztwór
NH
4
Cl
[NH
4
+
]
K
h
=
=
K
w
K
b
·
[OH
−
]
= 2 ·10
−5
2·10
−5
10
−14
=
= 5·10
−10
Jakie jest pH 0,4 M roztworu NH
4
Cl ?
[NH
3
·H
2
O] · [H
+
]
[NH
4
+
]
=
K
h
NH
4
+
+ H
2
O
NH
3
·H
2
O + H
+
=
tyle samo
=
małe
0,4 – [H
+
]
[H
+
] · [H
+
]
[H
+
]
2
= 0,4 · 5·10
−10
= 2·10
−10
[H
+
] = 1,4·10
−5
pH = 4,8
= 5·10
−10
=
[NH
3
·H
2
O]
[NH
4
+
]
· [OH
−
]
K
b
1
K
b
NH
4
Cl
H
2
O
pH~5
Wytrącający się
Cu(OH)
2
powoduje lekkie zmętnienie roztworu,
które można usunąć dodając niewielką ilość HNO
3
.
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
HYDROLIZA - podsumowanie
Hydrolizie ulegają sole których jony pochodzą
od słabych kwasów lub słabych zasad
W wyniku hydrolizy sole pochodzące od:
słabego KWASU dają roztwór ZASADOWY
słabej ZASADY dają roztwór KWAŚNY
Odczyn KWAŚNY mają również roztwory soli
wielu metali, których wodorotlenki są trudnorozpuszczalne.
Cu(NO
3
)
2
+ H
2
O
Cu(OH)
2(s)
+ 2HNO
3
Cu
2+
+ H
2
O
Cu(OH)
2(s)
+ 2H
+
Dlaczego? – REGUŁA PRZEKORY !
– cofanie reakcji hydrolizy.

Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
ROZTWORY
BUFOROWE
"BUFORY"
Bufory – utrzymują prawie stałe pH
pomimo znacznego rozcieńczania
lub dodawania ograniczonych liczności silnych kwasów lub zasad.
Roztwór buforowy powinien:
c) umożliwiać uzyskanie żądanego pH
b) zawierać także substancję zdolną do reagowania z jonami OH
−
a) zawierać substancję zdolną do reagowania z jonami H
+
oraz
(bufory – zderzaki)
d) nieznacznie zmieniać pH podczas rozcieńczania
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
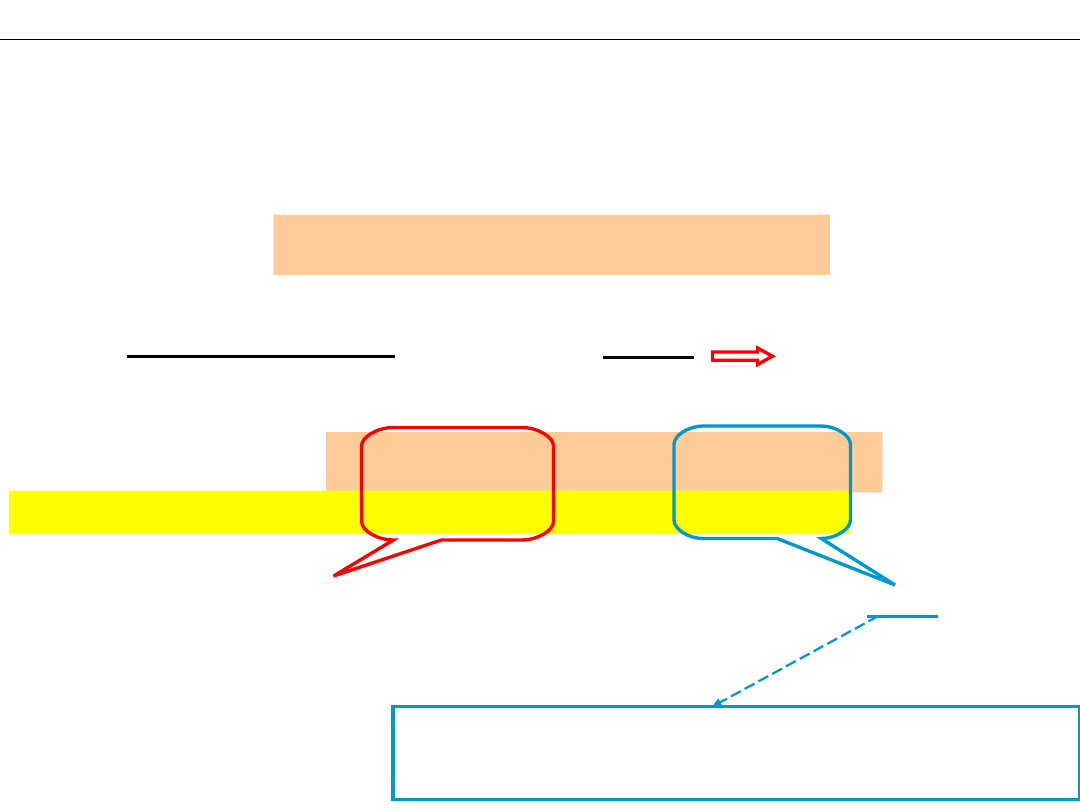
Czy 1,0 M roztwór kwasu octowego (CH
3
COOH) spełnia powyższe warunki?
Ile i jakich jonów jest w 1,00 M roztworze CH
3
COOH ?
CH
3
COOH H
+
+ CH
3
COO
−
=
[CH
3
COOH]
[H
+
]
· [CH
3
COO
−
]
K
a
= 1,6·10
−5
=
1,0
[H
+
]
2
[H
+
] = 0,004
CH
3
COOH H
+
+ CH
3
COO
−
0,004 0,004
0,996
Stężenia równowagowe:
Czy zawiera substancje zdolne do reagowania z jonami H
+
lub OH
−
?
Może reagować z dużą ilością OH
−
CH
3
COOH + OH
−
= CH
3
COO
−
+ H
2
O
Może reagować tylko z małą ilością H
+
CH
3
COO
−
+ H
+
= CH
3
COOH
Roztwór CH
3
COOH nie nadaje się na bufor –
trzeba zwiększyć liczność jonów CH
3
COO
−
.
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
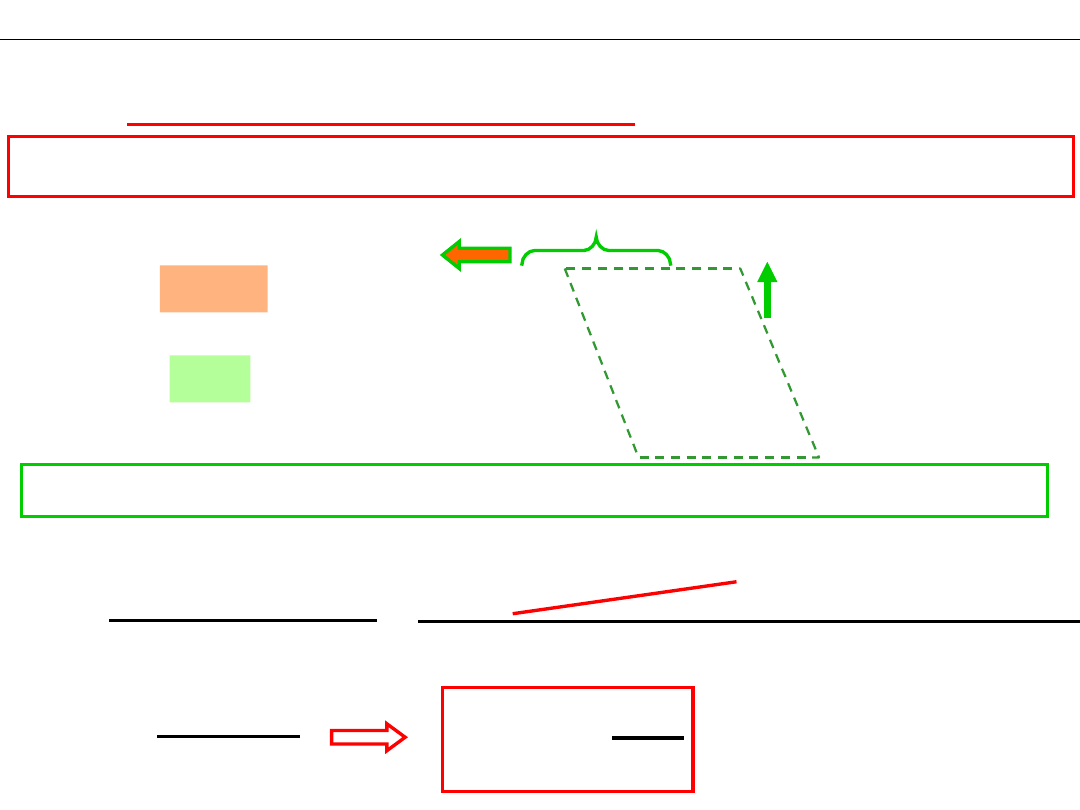
Do
c
k
= 1,0 M CH
3
COOH dodajemy CH
3
COONa o stężeniu
c
s
= 1,0 M
CH
3
COONa → Na
+
+ CH
3
COO
−
=
[CH
3
COOH]
[H
+
]
· [CH
3
COO
−
]
K
a
Dodanie soli CH
3
COONa cofa dysocjację słabego kwasu CH
3
COOH.
Roztwór CH
3
COOH nie nadaje się na bufor –
trzeba zwiększyć liczność jonów CH
3
COO
−
.
CH
3
COOH H
+
+ CH
3
COO
−
c
k
= 1,0 M
c
s
= 1,0 M
małe
<< c
k
=
[CH
3
COOH]
[H
+
]
· ([CH
3
COO
−
]
KWAS
+ ([CH
3
COO
−
]
SÓL
)
KWAS
SÓL
c
s
= 1,0 M
bardzo małe
=
c
k
= 1,0 M
=
K
a
c
k
[H
+
]
· c
s
[H
+
] =
c
k
c
s
K
a
wspólny jon
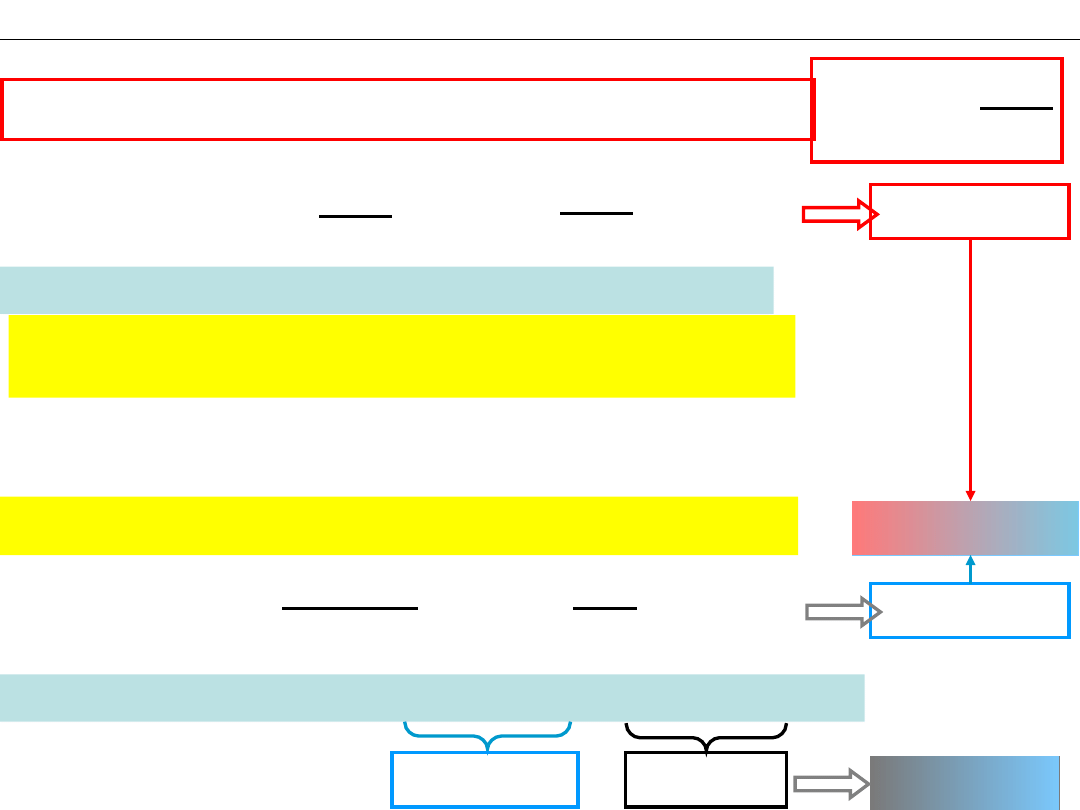
Zmiany stężeń
podczas reakcji:
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Roztwór
c
k
= 1,0 M CH
3
COOH i
c
s
= 1,0 M CH
3
COONa
CH
3
COOH + NaOH = CH
3
COONa + H
2
O
Jakie jest pH tego roztworu po dodaniu 0,1 M NaOH?
[H
+
] =
c
k
c
s
K
a
[H
+
] =
c
k
c
s
K
a
= 1,6·10
−5
1,0
1,0
= 1,6·10
−5
pH = 4,8
CH
3
COOH + OH
−
= CH
3
COO
−
+ H
2
O
– 0,1
– 0,1
+ 0,1
Stężenia po reakcji:
c
k
– 0,1
c
s
+ 0,1
[H
+
] =
= 1,6·10
−5
1,0 – 0,1
1,0 + 0,1
= 1,6·10
−5
0,9
1,1
= 1,3·10
−5
pH = 4,9
ΔpH = 0,1
Jakie byłoby ΔpH po dodaniu 0,1 M NaOH do czystej wody?
pH = 13
pH = 7
ΔpH = 6
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
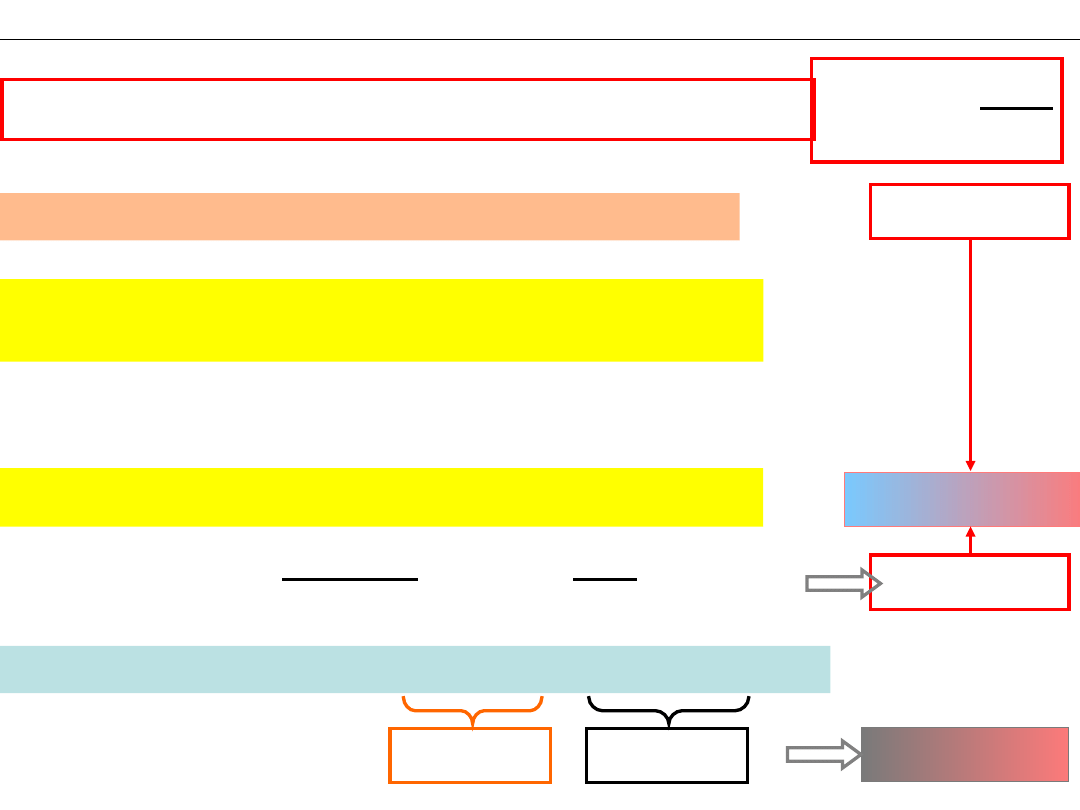
Roztwór
c
k
= 1,0 M CH
3
COOH i
c
s
= 1,0 M CH
3
COONa
CH
3
COONa+ HCl = CH
3
COOH + NaCl
Jakie jest pH tego roztworu po dodaniu 0,1 M HCl?
[H
+
] =
c
k
c
s
K
a
pH = 4,8
CH
3
COO
−
+ H
+
=
CH
3
COOH
Stężenia po reakcji:
c
k
c
s
– 0,1
+ 0,1
[H
+
] =
= 1,6·10
−5
1,0 + 0,1
1,0 – 0,1
– 0,1
– 0,1
+ 0,1
Zmiany stężeń
podczas reakcji:
= 1,6·10
−5
0,9
1,1
= 1,9·10
−5
pH = 4,7
ΔpH = -0,1
Jakie byłoby ΔpH po dodaniu 0,1 M HCl do czystej wody?
pH = 1
pH = 7
ΔpH = –6
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Roztwór
c
k
= 1,0 M CH
3
COOH i
c
s
= 1,0 M CH
3
COONa
Jak zmieni się pH tego roztworu po rozcieńczeniu n razy?
[H
+
] =
c
k
c
s
K
a
pH = 4,8
[H
+
] =
c
k
c
s
K
a
=
c
k
/
n
c
s
/
n
K
a
Stężenia
c
k
i
c
s
zmaleją n razy
pH nie zmieni się dopóki
stopień dysocjacji słabego
kwasu jest mały.
=
c
k
c
s
K
a
Czy pH samego roztworu można nieco zmieniać? – TAK zmieniając
c
k
/
c
s
Roztwór buforowy powinien:
c) umożliwiać uzyskanie żądanego pH
b) zawierać także substancję zdolną do reagowania z jonami OH
−
a) zawierać substancję zdolną do reagowania z jonami H
+
oraz
d) nieznacznie zmieniać pH podczas rozcieńczania
Roztwór
c
k
= 1,0 M CH
3
COOH i
c
s
= 1,0 M CH
3
COONa
jest
BUFOREM !
BUFOR „octanowy”
PODSUMOWANIE
Roztwór
c
k
= 1,0 M CH
3
COOH i
c
s
= 1,0 M CH
3
COONa
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
1. Bufor amonowy: NH
3
·
H
2
O + NH
4
Cl
Przykłady roztworów buforowych
NH
3
·H
2
O NH
4
+
+
OH
−
=
[NH
3
·H
2
O]
[NH
4
+
]
· [OH
−
]
K
b
=
· [OH
−
]
c
s
c
z
c
z
c
s
[OH
−
] =
c
z
c
s
K
b
2. Bufor węglanowy: H
2
CO
3
+ NaHCO
3
CO
2
+ H
2
O H
2
CO
3
H
+
+ HCO
3
−
c
k
c
s
=
[H
2
CO
3
]
[H
+
]
·
[HCO
3
−
]
K
a
[H
+
] =
c
k
c
s
K
a
Bufor węglanowy uczestniczy w utrzymywaniu pH krwi w zakresie 7,35 7,45
(
c
k
/ c
s
1:20)
20
= 9,0 ·
10
−7
1
= 4,5 ·
10
−8
pH = 7,35
c
k
[H
+
]
· c
s
=
[H
+
] =
c
k
c
s
K
a
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
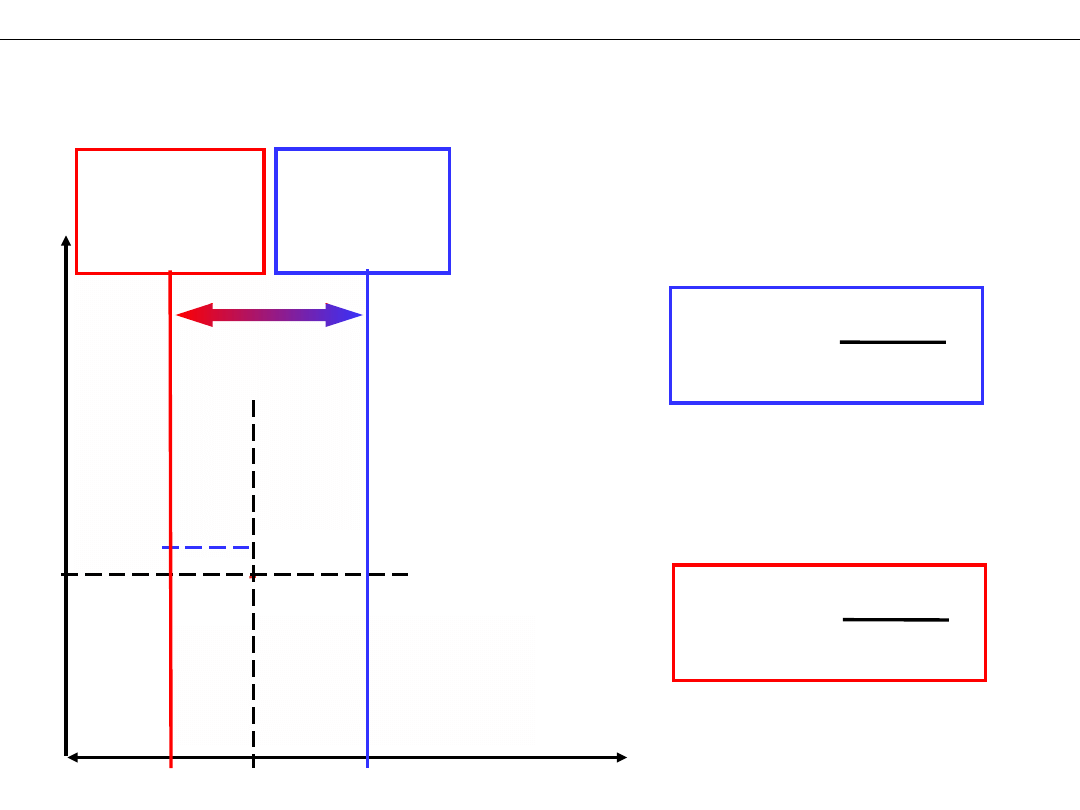
Zakres buforowania i pojemność buforu.
[H
+
] =
c
k
–
n
c
s
+ n
K
a
[H
+
] =
c
k
+
n
c
s
– n
K
a
Dodawanie silnej zasady lub silnego kwasu do buforu octanowego
1. Dodawanie silnej zasady
CH
3
COOH + NaOH = CH
3
COONa + H
2
O
2. Dodawanie silnego kwasu
CH
3
COONa+ HCl = CH
3
COOH + NaCl
pH
n
kwasu
n
zasady
0
0
7
14
na
kwas
ZAKRES
BUFOROWANIA
POJEMNOŚĆ
BUFORORU
na
zasadę
mało
kwasu
CH
3
COOH
mało
soli
CH
3
COONa
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
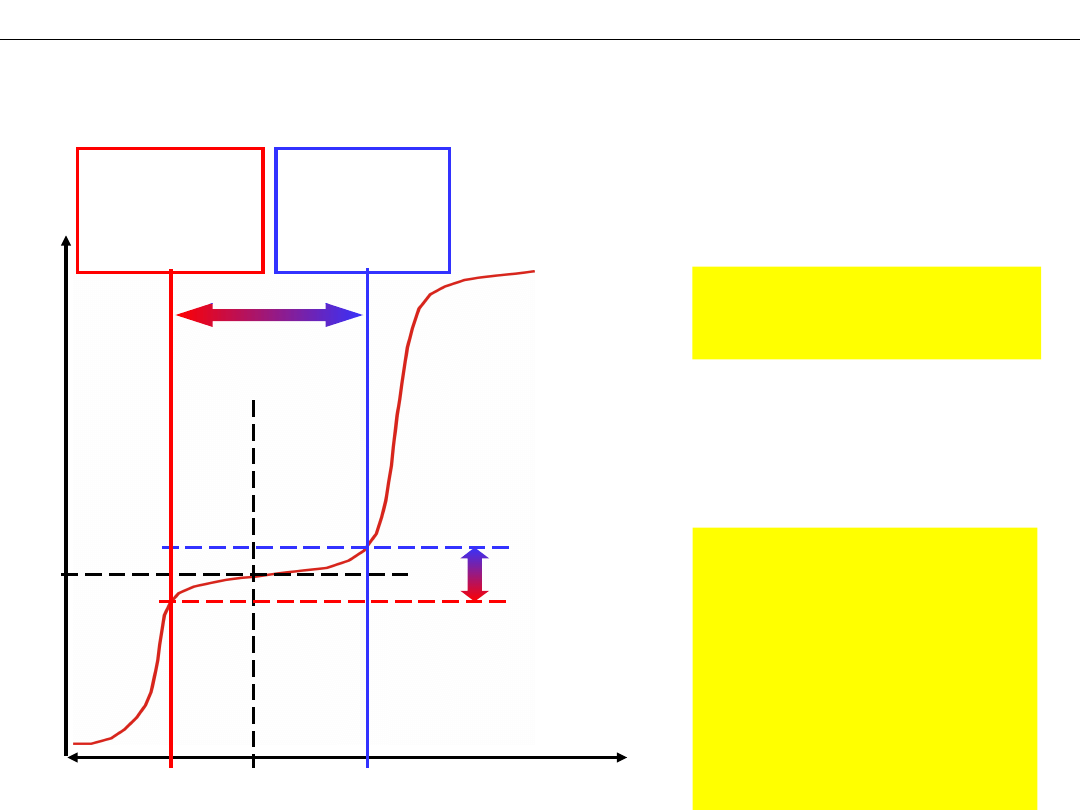
Zakres buforowania i pojemność buforu.
Dodawanie silnej zasady lub silnego kwasu do buforu octanowego
pH
n
kwasu
n
zasady
0
0
7
14
na
kwas
mało
soli
CH
3
COONa
ZAKRES
BUFOROWANIA
POJEMNOŚĆ
BUFORORU
na
zasadę
mało
kwasu
CH
3
COOH
ZAKRES
BUFOROWANIA
Przyjmuje się, że:
ΔpH = pK
a(b)
1
POJEMNOŚĆ
BUFORORU
Pojemność buforu na
kwas (zasadę) jest to
liczność mocnego
kwasu (zasady) jaką
należy dodać do 1
dm
3
buforu aby
zmienić jego pH o
jednostkę.
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
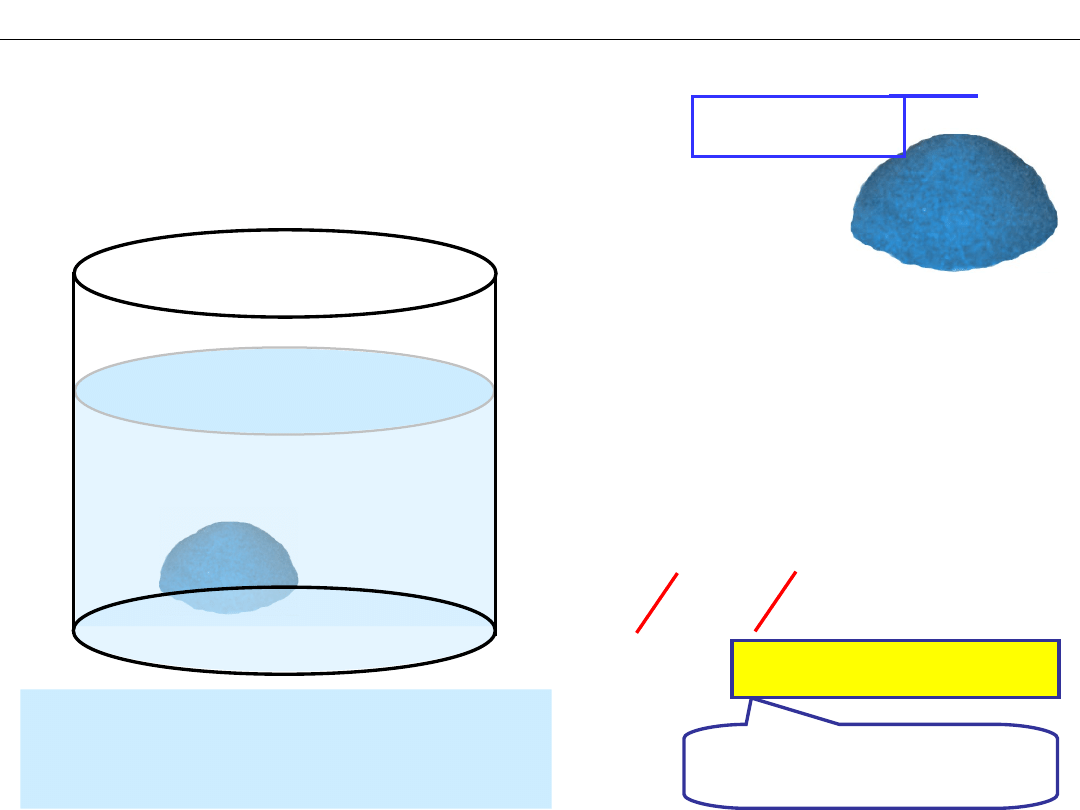
Równowaga w nasyconych roztworach soli
Cu
3
(PO
4
)
2
H
2
O
1. Rozpuszczanie
v
r
= k
r
S
S
–
powierzchnia
osadu
Cu
2+
PO
4
3−
Cu
2+
PO
4
3−
Cu
2+
PO
4
3−
2. Krystalizacja
v
k
= k
k
S [
Cu
2+
]
3
[PO
4
3−
]
2
3. Stan równowagi
v
r
= v
k
k
r
S = k
k
S [
Cu
2+
]
3
[PO
4
3−
]
2
k
r
/ k
k
= I
r
= [
Cu
2+
]
3
[PO
4
3−
]
2
ILOCZYN
ROZPUSZCZALNOŚ
CI
Roztwór NASYCONY
– ilość osadu i stężenia jonów
nie zmieniają się.
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Iloczyn rozpuszczalności stosuje się dla soli trudno (słabo)
rozpuszczalnych, gdzie w roztworze nasyconym stężenia jonów są
stosunkowo małe.
ILOCZYN ROZPUSZCZALNOŚCI
I
r
= [
Cu
2+
]
3
[PO
4
3−
]
2
=
1,4·10
−37
Reakcja rozpuszczania:
Cu
3
(PO
4
)
2(s)
3Cu
2+
+
2PO
4
3−
Jaka jest rozpuszczalność R (mol/dm
3
)
Cu
3
(PO
4
)
2
w czystej
wodzie?
3R
2R
= [PO
4
3−
]
= [Cu
2+
]
R
=
1,4·10
−37
/108
5
R
= 1,7 ·10
−8
mol/dm
3
R
I
r
=
[Cu
2+
]
3
[PO
4
3−
]
2
= (3R)
3
(2R)
2
= 27R
3
4R
2
= 108 R
5
= 1,4·10
−37
W 1 dm
3
rozpuszcza się
zaledwie
1/100 000 000 mola Cu
3
(PO
4
)
2
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
Czy 0,0001 M roztwór CaF
2
jest roztworem nasyconym?
pI
r
= 10,4
ILOCZYN ROZPUSZCZALNOŚCI
I
r
= [Ca
2+
][F]
2
= 4·10
–11
CaF
2(s)
Ca
2+
+ 2F
−
I
r
= 10
–10,4
= 4·10
–11
Sprawdzamy wartość iloczynu jonowego
[
Ca
2+
][F]
2
w danym roztworze...
[
Ca
2+
][F]
2
= 0,0001· (0,0002)
2
= 4 ·10
–12
... i porównujemy z iloczynem rozpuszczalności
I
r
.
4 ·10
–12
4·10
–11
<
Roztwór jest NIENASYCONY
[
Ca
2+
][F]
2
= I
r
– roztwór NASYCONY
< I
r
– roztwór
NIENASYCONY
> I
r
– roztwór PRZESYCONY
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
W nasyconym roztworze AgCl stężenie jonów Ag
+
wynosi
1,3
·
10
–5
.
Jak obniżyć to stężenie do wartości 1,0
·
10
–6
?
Efekt wspólnego jonu
I
r
=
[
Ag
+
][Cl
−
] =
1,3
·
10
–5
·
1,3
·
10
–5
=
1,69
·
10
–10
AgCl
(s)
Ag
+
+ Cl
−
Aby zmniejszyć stężenie Ag
+
trzeba
równowagę przesunąć „w lewo” – jak to
zrobić?
– dodać jonów Cl
−
Ile? – do jakiego stężenia? - X
Obliczamy iloczyn rozpuszczalności...
Po dodaniu jonów Cl
−
iloczyn jonowy będzie większy od
iloczynu
rozpuszczalności – roztwór przesycony – zacznie się
wytrącać AgCl, co obniży stężenie jonów Ag
+
aż do żądanego
stężenia 1,0·10
–6
.
.. który także musi być spełniony gdy stężenie Ag
+
wynosi 1,0
·
10
–6
I
r
=
[
Ag
+
][Cl
−
] =
1,0
·
10
–6
·
X
=
1,69
·
10
–10
X
=
1,69
·
10
–4
Efekt wspólnego jonu jest wykorzystywany w analityce
chemicznej do ilościowego wydzielania jonów lub
rozdzielenia ich mieszaniny.
Wykorzystanie
Reguły Przekory
W 1 dm
3
rozpuści się tylko 38 milionów cząsteczek HgS!
Wykład 14 –
HYDROLIZA, BUFORY, SOLE TRUDNOROZPUSZCZALNE
"Rekordziści" wśród soli trudnorozpuszczalnych
*
Wg: D.Z. Lide, Handbook of Chemistry and Physics-83th Edition, CRC
Press 2002.
DODATEK
SÓL
I
r
*
R
(mol/dm
3
)
CuCN
4,4·10
−20
2,1·10
−10
AlPO
4
9,9·10
−21
9,9·10
−11
ZnSe
3,6·10
−26
1,9·10
−13
HgS
4,0·10
−33
6,3·10
−17
Ca
3
(PO
4
)
2
2,1·10
−33
1,1·10
−7
Cu
3
(PO
4
)
2
1,4·10
−37
1,7·10
−8
Fe(OH)
3
2,8·10
−39
1,0·10
−10
Tl(OH)
3
1,7·10
−44
5,0·10
−12
Konkurencja 1- najmniejszy
I
r
1
2
3
Tl(OH)
3
Fe(OH)
3
Cu
3
(PO
4
)
2
Konkurencja 2- najmniejsza
R
1
2
3
HgS
ZnSe
Tl(OH)
3
HgS
R
HgS
6,3·10
–17
mol/dm
3
· 6,02·10
23
cząst./mol 38 mln. cząst./dm
3
Z roztworu usuwamy 1 000 000 000 cząsteczek w ciągu 1 sekundy.
Usunięcie 1 mola – około 20 milionów lat!
Usunięcie HgS – około 0,04 sek.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
Wyszukiwarka
Podobne podstrony:
14. Hydroliza soli. Sole trudno rozpuszczalne, Studia, Chemia ogólna, Wykłady
Wykład 10 bufory, sole hydrolizujące, alkacymetria 5fantastic pl
07 Hydroliza, bufory
Ćwiczenie 14 Hydroliza lipidów mleka
07 Hydroliza, bufory
2014Wyklad 8 bufory, sole hydro Nieznany
Wyklad 11b Elektrolity cd , hydroliza, bufory, iloczyn rozpuszczaln
Chemia fizyczna - Ćw. 13 i 14 - Dysocjacja, Dysocjacja, hydroliza, pH,
4 sole, Temat: Dysocjacja oraz hydroliza soli
Hydrologia cwiczenia 13 i 14
Hydrologia cwiczenia 13 i 14
Hydrologia cwiczenia 13 i 14
więcej podobnych podstron