Laboratorium Fizyki
Ćwiczenie nr 13
Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego
Krzysztof Nalborczyk
Paweł Mszyca
1. Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie wartości przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego.
2. Wstęp teoretyczny
Wahadłem rewersyjnym (odwracalnym) jest wahadło fizyczne, które zawieszone na dwóch ustalonych osiach obrotu O1 i O2 leżących po przeciwnych stronach środka ciężkości wahadła w nierównych od niego odległościach posiada taki sam okres drgań.
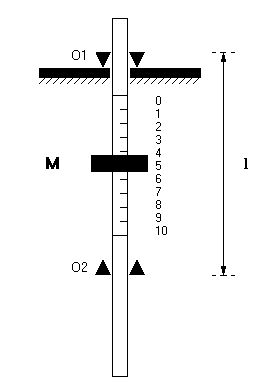
Biorąc pod uwagę, że zgodnie z twierdzeniem Steinera :
I = I0 + md2
gdzie :
I0- moment bezwładności wahadła względem osi przechodzącej przez środek ciężkości,
d - odległość środka masy od osi obrotu,
to przekształcając odpowiednio wzory na okresy drgań względem dwóch różnych osi oraz biorąc pod uwagę ich równe okresy drgań , powyższy wzór na okres drgań wahadła fizycznego przybierze postać wzoru na okres drgań wahadła matematycznego :
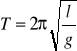
gdzie : l - długość zredukowana wahadła fizycznego.
Dla wahadła rewersyjnego , którego okres jest jednakowy dla obydwu osi obrotu O1 i O2, długością zredukowaną jest wzajemna odległość ostrzy t.j. odcinek O1O2. Po uwzględnieniu l = O1O2 z powyższego wzoru można obliczyć przyśpieszenie ziemskie :
![]()
3. Opis ćwiczenia
Przy wyznaczeniu przyspieszenia ziemskiego używaliśmy wahadła rewersyjnego, które miało postać stalowej sztaby , na której znajdował się obciążnik M w kształcie dysku. Rolę osi O1 i O2 pełniły metalowe pryzmaty zamocowane prostopadle do sztaby . Istniała możliwość przesuwu obciążnika M i tym samym możliwość zmiany położenia środka ciężkości wahadła względem osi . Odczytu położenia masy dokonywaliśmy przy pomocy skali naniesionej na sztabę . W trakcie przeprowadzania doświadczenia znajdowane jest takie położenie obciążnika przy którym okresy wahań wahadła względem obu osi stają się takie same . Wtedy to odległość między osiami staje się długością zredukowaną wahadła. Wahadło zostało zawieszone na ostrzu O1 .
W tabeli nr 1 znajdują się wyniki serii m = 10 niezależnych pomiarów czasów trwania tm dziesięciu drgań ( n = 10 ) w czasie których masa M znajdowała się na środku pręta . Tabela zawiera także wartość średnią czasów drgań t , średni błąd kwadratowy St pojedynczego pomiaru skorygowany przez współczynnik Studenta-Fishera :
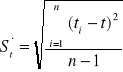
; ![]()
![]()
dla poziomu ufności ![]()
równego 0,95 i liczby n pomiarów równej 10 współczynnik wynosi 2,3 więc
![]()
t1 [s] |
t2 [s] |
t3 [s] |
t4 [s] |
t5 [s] |
t6 [s] |
t7 [s] |
t8 [s] |
t9 [s] |
t10 [s] |
t [s] |
St [s] |
tα,n |
St [s] |
17,66
|
17,62 |
17,59 |
17,65 |
17,65 |
17,59 |
1' |
18'78'' |
18'72'' |
18'71'' |
18'77'' |
0,042 |
2,3 |
0,097 |
Następnie ciężarek M był przesuwany począwszy od ostrza O2 w kierunku ostrza O1 co 5 cm ( kolejne położenia kn masy M były zaznaczone na pręcie przy pomocy lini ) a za każdym razem dokonywane były pojedyncze pomiary czasów t' dziesięciu drgań .Po wykonaniu wszystkich pomiarów wahadło obrócono, zawieszono na ostrzu O2 i wykonano podobne pomiary tym razem czasów t''.
Wyniki wszystkich pomiarów (tj. kn,t',t'') zamieszczone są w tabeli nr 2.
Tabela nr 2
kn |
[cm] |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
t' |
[s] |
20,18 |
19,90 |
19,84 |
19,68 |
19,42 |
19,28 |
19,16 |
18,85 |
18,77 |
18,63 |
t'' |
[s] |
20,17 |
20,02 |
19,62 |
19,23 |
19,04 |
18,65 |
18,54 |
18,25 |
17,96 |
17,72 |
kn |
[cm] |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
t' |
[s] |
18,74 |
18,56 |
18,66 |
18,68 |
18,90 |
19,00 |
19,30 |
19,53 |
20,01 |
t'' |
[s] |
17,33 |
17,37 |
17,40 |
17,63 |
18,15 |
18,83 |
19,57 |
19,74 |
19,86 |
We wspólnym układzie współrzędnych wykonane zostały wykresy t'=f(kn) i t''=f(kn).Krzywe zmian czasów t'=f(kn) i t''=f(kn) przecinają się w dwóch punktach t'0 oraz t''0 , które to odpowiadają takim położeniom masy M dla których okresy drgań względem obu osi są jednakowe . W punktach tych nasze wahadło fizyczne staje się wahadłem rewersyjnym . Z czasów t'0 i t''0 obliczono czas średni t0 oraz oszacowano błąd Δt0 przy pomocy następujących wzorów :
![]()
gdzie: ![]()
![]()
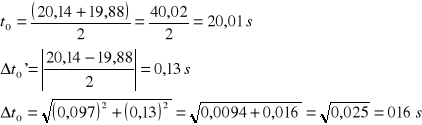
Obliczyliśmy okres drgań wahadła T0.
![]()
s
Obliczyliśmy przyśpieszenie ziemskie g i błąd bezwzględny Δg ze wzorów:
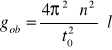
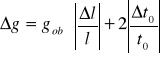
![]()
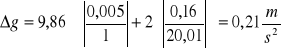
Końcowe wyniki obliczeń zostały zamieszczone w tabeli nr 3.
t'0=20,01 s
|
t''0=19,88 s |
t0=20,01 s |
Δt'0=0,13 s |
Δt0=0,16 s |
t0=1,88 s
|
l=1 m |
Δl=0,005 m |
g=9,86 m/s2 |
Δg=0,21 m/s2 |
Wykres:
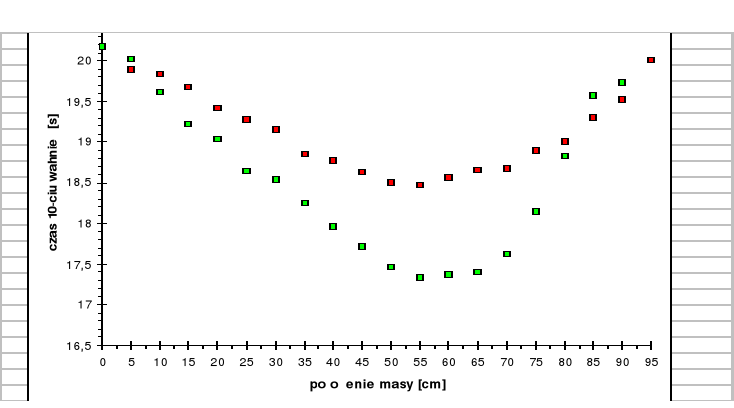
4. Podsumowanie
Wyliczone przyspieszenie ziemskie g odbiega znacznie od prawdziwego lecz mieści się w granicach błędu ( g dla południowej części Polski powinno wynosić ok. 9,8 m/s2 ) .Duże wartości błędów wynikają z niedokładności pomiarów czasu stoperem . W celu zmniejszenia błędów powinno wykonać większą ilość pomiarów dla większej ilości drgań .
Wynik ćwiczenia
Nasze doświadczenie dowiodło, że przyśpieszenie ziemskie wynosi:
g=9,86 ± 0,21 ![]()
Wnioski
Przeprowadzenie powyższego ćwiczenia pozwoliło nam na dokładniejsze zaznajomienie się z zagadnieniami dotyczącymi przyśpieszenia ziemskiego i grawitacji. Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej. Innym czynnikiem wpływającym na lokalne zmiany wartości przyśpieszenia jest zmienna gęstość Ziemi oraz wysokość nad jej powierzchnią.
Bez względu na metodę pomiarową i dokładność użytych przyrządów nie można wyznaczyć dokładnie wartości liczbowej mierzonej wielkości lub jest to bardzo trudne. Wskutek niedoskonałości przyrządów , metod pomiarowych i wreszcie naszych zmysłów, refleksu popełnia się błędy ,których uniknąć jest niemożliwe. Wielokrotne pomiary tej samej wielkości fizycznej daną metodą dają różne wyniki liczbowe., mają na to wpływ przyczyny przypadkowe, nie można ich ani przewidzieć ani określić liczbowo.
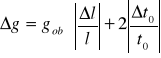
Wyszukiwarka
Podobne podstrony:
w.85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 40, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
cwiczenie61a, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYKA75, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
F-85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
tabele do cw 36, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 13, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
CW85GRZ, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
LAB3 61, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
lab cw12, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
jola 66, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 85, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
SPR F 56, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
sciaga fizyka kolos 1a, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYK 75, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
FIZYK 61, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
CW56, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
więcej podobnych podstron