Maszyna hydr (przepływowa)

Urządzenie,wkt zmienia się energia

całkowita przepływającego płynu (cieczy) wskutek wykonania przez płyn pracy

mech lub wskutek pobrania przez płyn en mech.Chodzi tu o bezpośrednie przekaz

ener do płynu(maszy robocze,went,

sprężarki, pompy) lub od płynu (turbiny wodne, parowe lub gazowe). Płyn styka się

bezpośrednio z eleme maszyn, wywierając na elem maszyn odp siły i momenty

Teoria maszyny przepływowej -zespół równań (związków) wyrażaj oddaną przez maszy lub dostar do maszy energię mech w funkcji parametrów geometr i kinemat maszyny oraz parametrów płynu na wlocie do maszyny a więc w funkcji kształtu, wymiarów, liczby obrotów oraz ciś na wlocie prędkości.Silniki przepływowe

turbinywodne,parowe,gazowe,Maszyny robocze - pompy tłokowe, wirowe

wentyla (osiowe, promieniowe itp.)

sprężarki,dmuchawyTurbiny wodne -

natryskowa tzw. turbina Peltona

naporowa,tzw.turbinaFrancisa(promienioa)

turbina Kaplana (osiowa,Eltona, Francisa

Kaplana Pompy tłokoweZasada dział -

okresowe przenoszenie ściśle określ objętości cieczy z tzw. Obszaru ssania do tzw. Obszaru tłocz.Przemieszczenie cieczy

wywołane jest odpowiednim ruchem

organu czynnego pompy tj. tłokiem. W pompach tłok dostar tłokowi ene mech zamieniana jest bezpośrednio na energ pot cieczy,w szczegidzie ona na przyrost ciś staty Pompy wiroweSkł się z 3 części: wirnika, kierownicy i korpusu. Kierownica nie zawsze występuje, a jej role odgrywa odp ukształt korpus tzw. Spirala wylotowa.

Zasa działa: polega na zwiększeniu ene kin cieczy przepływającej przez pompę, a nastepnie przeksztener kinet na ciś w kierownicy lub w spirali wylotowej

Równania Bernoullieobilans ene cieczy przez wirnik:

ρghL wart ene mech jaką oddaje lub pobiera 1 kg płynu w jedn czasu przepływając przez wirnik. Przy czym ene oddana przez płyn ma znak dodatki (silniki), zaś pobrana przez płyn ujemny (pompy, wentylatory). Obliczmy zatem następnie przyrost ciśnienia p1-p2 podczas przepływu przez wirnik.równanie Bernoul w ukł związanym z wirnikiem, w tym ukł ruch może być traktowany jako ustalony

potencjał sił odśrodkowych i masowych

Równanie teorii maszyn wirnikowych

Moment działający na wirnik

Zgodnie ze wzorem na moment

ၳ - pole powierzchni łopatek

Drugie równanie maszyn przepływowych

M = ρ Q (r₁ c₁ cosα₁ - r₂ c₂ cosα₂) = ρ Q (r₁ c_1n - r₂ c_2n)

Praca mechaniczna w jednostce czasu (moc)Mω = ρ Q ω (r₁ c_1n - r₂ c_2n) = h_L ρ g QJeśli M i ω zwroty zgodne, praca dodatnia → silnik M i ω +/- zwroty przeciwne, praca ujemna → maszyna robocza SprawnośćRozporządzalna wysokość cieczy H tylko częściowo można wykorzy na wytworz w silniku en mech użyte, część naporu e idzie na pokonanie opoow ruchu wywołanych lepko płynu, pozostała część wysokości H na wytworzenie nergii kinet v2/2g, z jaką płyn opuszcza rurę ssąca.dla silników można napisać

Sprawność ၨH energii mechanicznej wytworzonej w urządzeniu do rozporządzalnej wys H

Wtedy równanie podstawowe silników hydraulicznych będzie

Podobieństwo przepływu przez maszyny przepływowe Rozważmy - Stacjonarny przeplyw przez dwie maszyny, które są geometrycznie podobne, ale mają różne wymiary i różne obrotySkala wymiarów liniowychλ = d₂/d₁Skala obrotów(czasu)ν = n₂/n₁Aby przepływ był kin podobny, to trójkąty prędkości w obu maszynach

powin być podobne

stosunek wydatków

Zakładając równe sprawności obu maszyn obliczymy stosunek sprężów

bo

Podobnie stosunek mocy

Wyróżnik szybkobieżności - podsta param podob masz przepł, naz liczbe obrotów wzorcowej maszy przepływowej podobnej geom do konkretnej rozpatrywanej masz i rozwijającej jednostkowa moc przy jednostkowej spiętrzeniu (wysokości, naporze). W tym celu rugujemy l ze wzorów na podobieństwo (spiętrzenie i moc) i otrzymamy wtedy: Otrzy wtedy

wyróżnik szybkobieżności N [kM] n [obr/min] H [m]

dla silnikówWyróżnik dla maszyn roboczych zamiast mocy N wydatek Q

Ruchem turbu ruch cieczy odp brakowi stateczności rozwiązań stacjon a odznacz się nieregu i szybko zmien się w czasie liniami prądu. trudności wn rozwi

niestacjon ukł równań zrodziły koncepcję opisu r tur w oparciu o uśrednien parame przepływu. Doprowadziło to do r R.

Teoria turb jest oparta o tą koncepcję uśredniania przepływu.Uśredniane par przepływu są łatwo mierzalne, co umoż łatwą weryfikację eksperymentalną.

Rów Rey nie są niestety zamkn, stąd koniecz sfor dod równ ,modeli turbui.

Stąd też wynikła konieczrozpatrywania uproszczonych r Naviera - Stokesa np. równań warstwy przyściennej.

Roz r Naviera - Stokesa należy traktować dla przypadku r stacj np. przepływ Hagena - Poisseuille'a jako pewnego rodzaju abstrakcję. Takiego idealnego r nie spotkamy ani w naturze, ani w technice.

R pły są w rzeczy niestacj. Ruchy takie jako przepły stacj realizuje się tylko wtedy, gdy są statece (stabilne) wzglę małych zaburzeń. Przepły stabilne wzgl małych zaburzeń nazywa lam(przesuwające się po warstwach, bo lamina- warstwa).

przep niestab i nieuporząd przep tur.

Doświadczenie Re dowód niestabi i przejścia do turbulencji Szkla rura z zawor z1 regulacyjnym wydatek wody ze zb A, z B z zaw z2 z zabarw cieczą o tym samym ciężarz (gęstości). Ciecz tę można wpuszczać do rury szklanej regulując zawór z2. Jeśli wydatek wody jest dost mały, to smuga zab cieczy jest prostol, nie miesza się z wodą i sprawia wrażenie nieruch Przy wzroście wydatku wody smuga barwna traci nieruch, zaczyna oscylować i falisto wyginać się, nie mieszając się z wodą, granica smugi i otaczającej wody jest ostra i nie rozmyta

 Zwiększając dalej wydatek wody smuga miesza się z wodą tuż za wylotem rurki doprow zabarwioną ciecz Reywprowadził podział na dwa rodzaje ruchów:

Lami cieczy nie mieszają się ze sobą, ślizgają się po sobie na kształt łusek

Turb (burzliwy) - niestacjona, przypadi chaotycz to główne cechy toru elementów płynu całkowicie różne od siebie, nie można wyróżnić tu niezależn warstw, występuje silne mieszanie oprócz ruchu głównego. Wzdłuż osi przypadkowe ruchy w poprzek strumienia.ruTurbu charakt się dużym chaosem, miesza się warstw płynu.

R turb płynu opisuje się równaniami Rey,

otrzymanymi w procesie uśredniania r Naviera - Stokes'a.Jeżeli dla dowolnej wielkości charakteryzj przepływ (prędkość, ciśnienie, gęstość) założ, że jej wartość chwi skł się z wart uśrednionej w czasie i odchylenia od niej tj. fluktuacji

Równ.tur.r.płynu tensora naprężeń turbulentnych:

Dla przep ściśl należy ponadt uwzg fluktuacje gęsti i temp

Hipotez zamyk wnoszą do ukł rów nowe rów będące wyra zasto modeli turb, pon opisują one włas płynu - podobnie jak hipoteza New lepk płynu, to rów te można zalic do r konstyt charaktery pzepływ tur

Tens napręż Reyn

Prze tur

W pobliżu ścianki cia stał A = 0, pulsacje turbu przy ściance są =0 w pewnej odległod ścianki mogą przybierać wartości wielokrotnie wyższe od ၭ. Dlat opory prze tur są >od oporó prze lam. Źródłe

dodat napręż stych jest wymiana pędu między warstwami pły, repr przez uśre ilocz pulsacji skład prędkości. R Naviera - Stokes'a opisują lami i niesta r płynu,. R Rey są wypr z r NS.R tur jest zawsze trójwy i niest. Rozwiązanie rRey nie jest proste, gdyż wy dodat waru na skł tensora naprężeń turb. Tensor naprę trbu prowadza do rRe 6dod niewiad  Roz problemu, to kreowmodeli turbj-hipotzyłączące tensor naprężeń turbu z uśrednionymi charakter pola prędkości, zwykle charakter empi- uśrednianie przeksz r N S i analiza zw korel pomiędzy nimi, są to modele anali

 Model Bousinesqa

ၭB - lepkość tur, wg Bous wiel skal tensr prędkości odkształceń uśrednio

Hipotez ta postuluje istni „płyturbu”

Mod Prandtla - drogi mieszania

Doty jednowymi przepł ścinającego.

jeśli

to

- droga mieszania

Wiry turb zderzają się ze sobą na podobień zderzeń międzyc, droga mieszania jest analogiem drogi swobodnej rcząsteczek.

Prandtl postulował lp = ၫ y,ၫ - stała wyznaczana emp,w m P współczy lepk ależy od grad prędk.

Model von Karmana

Dot przep ścinającego daleko od ściany Jako funkcje droga mieszania

Mo Kołmogorowaza pomocą analizy wymiarowej dla turb izotropowej i jednorodnejSą one jednak niezależne od równań NS, stanowią pewien emp m turbui. l - skala dużych wirów, skala zew turbၨ - skala małych wirów ulega dyssypacji lo- skala molekularna, okreś lepk molek.

Tur proces podtrzy przez przekaz ene r główo do dużych wirów o skali l, a następ ich rozpad poprzez coraz mniejsze wiry aż do skali ၨ, które ulegają dyssypacji dzięki lepko zmieniając formę ene kin tych wirów w ene cieplną na poziomie skali lo

ၸ - skala molekul, określ lepk mol.

Intensywność dyssypacji: moc dyssypacji na

jednostkę masyၱ - temp

Na poz wirów dyssypujących się w skali ၨ siły bezwła są tego samego rzędu co siły lepki, bo l Rey =jest jedności.

Proces przekazywa en r głó do pozio dysypcji następuje z Intensywn określintensy dysypacji ၥ

Model k-ၥ (Spalding - Launder)inaczej m dwurówSzeroko stos w oblicz numer.

Opiera się na dodat półempirh równa

k - ener kinet r fluktuacyjnego płynu

  ogólnie lepkość tur

ၮt = ၮt (k, ၥ) , a więc

ၥ - prędkość dyssypacji

Równania na transport ၥ i k

Stałe są wyznac przez poró z wynikami eksper w stosun prost geometrih, jak ślad aerodynay lub prosty kanał.Są to ró transportu ၥ i k, endysypacji i ene kinetj fluktuacji. Podob geome 2obiekty geomet są podobe, gdy można dobrać tak ukł współ dla obu obiek aby każde punkt jed ob odp jed i tylko jed pu drugi ob.=stos współrz odp sobie punkt jest stały.

Oba ukł muszą być jednakowe pod wzgl formalnym (prawo- lewoskręt jednocześ)

równa ciągłości

 

Równanie pędu

Kryter podobień 2 przepływy stacj cieczy lepk będą pod, gdy 1 Powierzch graniczn będą geomet podob2Bezwymiarowe stałe param utwore ze stałych i charakterysty dla przepły wielkości po, Vo, ၲ, ၮ, l , i będą jednak dla obu przepływ

3Kierunki prędkości wzgl powierzchni brzeg w dwu odpowiadających sobie punkt będą jedn
Np.przepływy przez rurę prostoosiową będą równe, gdy

 

Są to kryte podob rozpatrywanych przepł lamin.Bezwymi kombina wielkoś fizycz stanowią o podobień naz parame podobie .Kryteri podobień oznacza równość odpowied paramet podobi porównywanych zjawisk.Parametry te noszą nazwy od nazwisk uczonych,kt pierwsi je wprow i uż

Opór ciała opływanego cieczą lepką

Całka po całej powierz ciała i po wprowadz wzorów na składowe

Opór cieśn., opór tarcia

opór całkowity X jest sumą dwóch składnikówX = Xc + XT. W cieczy nielepk opór tarcia Xt = 0, bo niewystęp naprężen stycz, opór ciś na mocy parad d'Alamberta jest=0.W cieczy lep oba składniki oporu są rózne0.Pojęcie oporu profilowego Xp

 Różnica pomięd opor całko ciała X opływanego cieczą lepką a oporem Xid jakiego doznawałoby ciało opływane cieczą dosko bez obszaru zastoju X = Xp + Xid.W przepł płaskim opór całk ciała o wymiar ogranicz jest = oporowi profilowemu bowiem opór Xid jest=0 na mocy paradoksu d'Alamberta. Podobnie jest dla ciał płaskich półnieskończonych.

Oderwa warstwy przyśc (laminj, stacjon)

 Wynika bezpośre z r Prandtla i warunków brzegowych. W punktach na ściance,

gdzie

Podstawowa różn:

Krzywa wypukła

Krzywa ma punkt przegięci

Oderwanie przepływu nastąpi w przyp 2 a), czyli jako obszar z uje prędkością u(y)

Interpre,2 siły działają na element płynu porusz się wzdłuż ścianki-1siły tarcia o ściankę2siły normalnej do ścianki ciała stałego wynikaj z różnicy ciś na przed i tyl ściance elem płynu .W przypadku dp/dx > 0 obie te siły są przeciwne do zwrot prędkości elemen płynu. Element traci swą en kin i zatrzye się, a elementy podążające za nią (i on sam) odrywają się od ścianki.

Dla dp/dx < 0 siła wyn z różn ciś na przedn i tyln ściance elementu jest zgod z prędk tego elementu i oder nie następuje. Opływ wokół profilu:1bez oderwania2z oderwa

Warstwa przyścienW przypadku dużych licz Rey nie można linearyzować równania NS za pomocą uproszczeń prowadzących do równa Stokes'a i Oseena tj. odrzucenia członu nieliniowego lub zostawienie tylko jego części

Każda część członu nieliniowego może być większa od * , zaś odrzucenie członu *၄v/Re prowadzi do równania Eulera, a więc w ogóle nie uwzględnia lepkości.

Koncepcja PrandtlaW całko obszarze przepły wyróż 2podobszary:1sąsiedztwo ścianek ciała - warstwa przyścienna (graniczna), siły lepko są co najmniej tego rzędu co siły mas, wpły na r płynu2obszar poza warstwą przyścienną, w kt siły lepki są pomijalnie małe w porównaniu z sił masi, płyn w tym obszarze może być trakty jako nielepki ၤ -grub wars przyścij - odleg od ścianki punktu, w kt prędkość przepły różni się nieznacz od prędko przepły potenco, zwyk jest to różnica ~ 1%

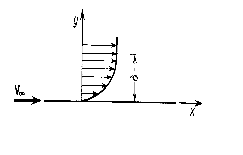
CzylivA = 0,99 vCD, tj. vCD - gdyby ciało było opływane cieczą dosko.Równania Pradtla-uproszczone r NS.Dla dwuwymia ustal ruchu

równanie ciągłości

równania ruchu

Ocenimy rząd wielkości poszczegó skład w tych równa w obszarze warstwyprzyście opierając się na założeniu, że grubość warstwy przyśj jest mała. Wyrazy i są

małe i odrzucamy je

Porównajmy siły bezwł (masowe) i siły lepk

są tego samego rzędu w warstwie przyś. Niech

co oznacza, że gru warstwy przyś jest odwrot propo do l Rey.Zgodnie z drugim równ ciśn w war przyścj jest stałe wzdłuż normaj do ścianki, co ozna, że ciśn w war przyśc jest=wartości ciśn przepł

„nielepkiego” na granicy warstwy.

równ Prandt dla dwuwymia wars

przyścj z przepły stacj. Przepływ na zewnątrz warst przyśj może być potencjalny lub wirowy, traktując go jako nielepki można wykorzys róe Eulera

kt obowią na ściance ciała opływa cieczdosk. Z tego rów dla przepł ustalo

Podstawiając do dalej

otrzymamy następnie rów Prandtla

Opływ zadanego ciała cie lep można podzielić na2następe zagadnienia (w oparciu o koncepcję war przyścj i r Prandtla)1Wyznaczenie przepływu nielepk wokół ciała (np. przepływ potencjalny) a w szczei wyznace rozku prędk u wzdłuż ciała lub ciśna2Wyznaczenie rozwinięcia u(x, y) i v(x, y) r Pradtla przy stosownych war brzeg.Warunki brzeg dla r Prandtla

u(x, 0) = v(x, 0) = 0;u(x, ၤ) = u(x)

Drugi warunek jest uzgodnieniem prędi na granicy wars przyśej i przepływu zewnęto.

Należy uzupełnić warunkiem u(xo, y) = uo(y)określającym rozkł prędci na pew linii łączącej ściankę z granicą warstwy. Rozkd prędści musi być zatem zadany w pewnym przekroju x = xo warsy, a rozwiąia dają przedłużenie tego rozkłu na inne wartości x. Przejście lamno turbtne w warwie przyścej.(eksnt)proces silnie nieliniowy rozpocący się etapem liniowego wzrostu zaburzeń tzw. fal Tollmiena - Schlichtina. Nastnie tworzie się3wymiarowych zaburzeń aby skończyć pojawieniem się tzw. plamek turbulencji, kt wreszcie „zlewają się” w przepływ turbtny Typy przejścia laminarno-turbulentnego1Naturalne (przepływ zewnęny z bardzo małym pozim zaburzeń)

2by-pass zależne od poziomu zabureń w strumiu zewym w stosu do warwy przyśnej

Fala uderzeniowaRozchodzenie się zaburzeń w gazie ruchomym1prędkość poddźwiękowa2naddźwiękowa3przepływ poddźwiękowy.Zaburzenia (fale) dźwiwe rozprzeniają się po całej przestrzeni

b)przepływ naddźwiękowy.Fale dźwiękowe (kuliste) wypełniają stożek o wierzchołku O i nie wydostają się poza stożek Macha Czoło fali uderzeniowej - najwize znacnie w aerodynamice przepłów naddźwih.Przez tę powierzhnię przepływa gaz v1u Ⴙ 0;v2u Ⴙ 0(gdy v1u = v2u = 0, powierzchnia poślizgu).Zmieniają się skokowo vu, ၲ, p

czoło fali uderz

Powsta prosdłej fali uderzej w rurze z tłokmGaz idealny, doły poczwo w spocku.

Tłok zaczyna się przezczać z prścią v, to powuje zaburnie (zgęszcie) gazu przed tłokiem i jego ruch (gazu) z pełną prędcią. Obszar zaburzeń powiza się z czasem, czoło fali propaguje się z pewną prędkścią u(t), poza tym obszarem gaz dalej nierucmy.W obszarze zaburzeń parary gazu zmieają się tzn. są f współrej x i czasu t. Prędkć propagacji zabzeń w każym przekroju x i w różnh chwilach czasu inna i=lokalej prędkości dźwięku a. Zmiana pararów doknuje się adiabatnie, izentowo, sprężaniu się gazu towarszy nagrzewnie się gazu. Ponieważ a ~ , a więc każda nastna fala przemieza się wzglem gazu z nieco więkzą prędkią, zatem jedna fala dogania drugą i nakłada się na nią. W rezultacie po pewnym czasie od uruchomnia tłoka tworzy się powierznia silnej nieciągłości paramów (nie tylko skokowa zmiana pochodnych ale i samej funkcji).Interesuje nas zmiana parrów gazu po przejściu fali.F uderzwa traktowana jest jako powiehnia, w gruncie rzeczy jest to warstwa o grubości drogi swodnej cząstzek gazu. ၲ1 v1 = ၲ2 v2

Ukła zamęty,3ównania i 3niewiadome p2, ၲ2, v2.Ruguąc prędkości otrzyy re adiabaty uderzeniowej Hugoniota

Przejście f uderej puje wzrost ciś, gęci i tempry, natst prędkość maleje. Proces sprężania nie jest izentroy, zachozi nieodwracalna przena enii mechj w ciepło, nawet dla gazu idealnego a zatem i przyrost entropii

Ściśliwość cieczy i odkształcalność rurocu mają tu istotne znaczenie, natoast pominiemy siły maswe i tar.Zdefinuj

rozprzeianie się małych zaburzeń w rurociągu

a - prędkość rozprnia się małych zaburzeń

Definiując następnie funcję ciśnia

Wyrażenia c1 = P + u i c2 = P - u tzw. niezmienniki Reimanna.Jeśli w rurociągu w chwili to nastąpi nagłe jego zamięcie, to w chwili zamcia p = po, i u = 0, co oznacza, że wartość c2 = 0 rozprzeenia się w górę przepływu, a c1 = 0 z prędkością u + a zgodnie c2 = 0 oznacza skąd p = po + ၲo u a

skąd p = po + ၲo u a

p = po + ၲo u a - fala ciśnienia tzw. Udere hydrauneNatomiast w dół przepływu rozprzestia się fala rozrzedzeniowa, c1 = 0,

a zatem p = po - ၲo u a

groźniej z obu fal jest f ciśna, bo może zniszczyć rurąg,natost f rozrzedzwa może spowwać co najwyżej kawitację. Dla częściego zamkcia rurociągu u = uo - ၄u w chwili to, c1 = - u + ၄u

Z uwzglem lepści f ciś będzie słabsza, bo lepść doprdzi do pewnej dyssypacji enii.

Środki zabezające przed konsami udeia hydrago1biorniki powrzne2wieżewyrów

3awory bezpiecza4rzedłużenie czasu zamykia (otwinia) zawu skrócie dł przewodu.Zawórbezpieczewa - otwiera się podczas udera hyd i wypuszcza część wody z rurociągu, a więc obniża ciśnie w rurociągu Niestacjonne przepływy w rurociągachUderz hydraune.Metoda przepływów1ymiarowych - chętnie stos w hydrae, jako uproszczenie m

3ymiarowego.Dokładność tego modelu zależy od precyzji definicji wartości średnich stosoych w metodzie 1ymiarowej.

Zalety:1prostsz równa + łatwo uzyskiwane rozwiia obarczone jednak często bliżej nieznnym błędem2syntetyczość informacji i rezultatówW hydraulice wiele modeli jest 1ymiarowych, dokładność rezultatów wystarczająco dobra.Objtość płynna w 1 D modeluRównania zachowania

Dowolny parametr P i jego zmiana w czasie

prędkość średnia

Deformacja liniowa elementu płynu

Przekształcając można uzyskać inne postacie róa ciągłości

lub po uwzględnieniu rówia zachania masy:

Przepływ niestacjonarny dla rurociągu

Uwzględniając ściśliwość cieczy i odkszlność rurgu, w ukł będzie za mało rówń, bo tylko 2, a 4 niewiadome u, ၲ, S, p.Znajdźmy te dodwe związki

Ec i ES moduły sprężystości cieczy i materiału rurociągu.D/d- stosunek średnicy rurociu do gruci ściankiMamy cztery rówa.Konieczne są poza tym warunki początkowe:p = p(l);u= u(l)

i warunek brzegowy: określenie na każdym z2ońców rurogu jednej z funkcji p = p(t) i u = u(t).Wzasadzie należy ten ukł równ rozwiązać numerycznie. 1przypdek tzw. uderie hydrczne można rozwiązać analitycznie. Ude hydraue tj. nagłe zamknięcie zaworu na rurociągu. Wówczas mamy do czynienia z gwałtom przyrostem ciśna w miejscach zamcia rurociągu i rozprzestrzeniem się fali ciśnienia w górę rurociagu. Przepływy w kanałach otwahdzieli się na naturalne i sztuczneNaturalne - rzeki, strumienie, potokiSztuczne - kanały kanalizacyjne, melioracyjne (nawadniające, odwadniające), komunikacyjne

 Różnice między przepływem w przewodach a kanałach otwartych:

W przewodzie płyn wypełnia cały przerój poprzzny przedu, w kanale otwym ciecz wypeła tylko część tego przekoju niezależe, czy jest to rurociąg czy odkryty kanał. Zatem w kanale istnieje swobodna powierzia cieczy, na powierni cieczy jest zwykle pewne ciśnie, najczęiej ciśn atmosfee Przepływ w kanale otwaym odbywa się wyłącznie pod działem siły grawicji, bezwłści i taria, musi też wystpić spadek dna wzdłuż jego dłuciW kanałach otwartych trudne jest analityczne ujęcie ruchu,w kanałach naturalnych niemoże ze wzglu na nieregulść koryta kanału i nieznaną chropotość. Rozważania ograniczymy do kanałów sztucznych.Ruch

wody w kanałach1zmienny(nierówmier

2jedostajny (równomierny).Gdyprzekrój strugi ulega zmianie - r zmienny

Gdy przekrój strugi stały - r jednostajny

 R zmienny - ustalony lub nieustalony (zmienny w czasie)Rozpatrujemy dalej tylko ruch jedny, ma on najczęściej charakter turbulentny.Odcinek początk Lp - na takim odcinku formuje się ruch.

v2 = const h = const.Analizadługości odcinka początego możliwa tylko na podstawie rozwiązania równań N S

Równanie Bernoulli'ego dla przekroju 1 i 2

hstr - różnica pozio równoważna wskutek tarcia na długości L.Dla ruchu jednostego linie prądu, w tym i powierhnia swobodna, są równoległe do dna, a więc p1 = p2 i v1 = v2 i wtedy hstr = ၄h = z1 - z2

 Spadek hydrauliczny

I = i = sinၡ - ၡ kąt nachylenia dna do poziomu.Podaje się go też w % lub ‰.

Wzór Chézy'ego - średnia prędkość przepływu

 

c - współczynnik Chézy'ego , rH - promień hydrauliczny [m]

 Strumień objętości wody

Opór tarcia w przewodach wg wzoru Darcy - Weissbacha

Skąd można wyznaczyć

Zwykle w obliczeniach nie korzysta się ze współczynnika ၬ, a tylko bezpośrednio ze współczynnika Chézy'ego c.

Rozkład Bazina prędkości

 

ζ- współczynnik doświadczalny zależy od h i spadku hydrnego

i dalej

Głębokość , gdzie występuje

na głębści 0,58 h należy mierzyć prędść średą .Najkrótszy obwód z wszystkich figur o tej samej powierzchni ma koło.

 Najczęściej stomy jednak przekroje prostokątne lub trapezowe.A więc dla przekroju prostokątnego A = b h

promień hydrauliczny

 

Optymalny przekrój prostokątny jest więc, gdy h = b/2

Czyli musi istnieć hkr dla którego ho = minimum. Głębść krytya hkr i ruch kryzny dla tej głębokości. Prędkość krytyczna

 

Przekształcając

liczba Froude'a, (kwadrat liczby Froude'a)

Energia strugi osiąga min, gdy liczbaFr= 1.

 Analizując wykres, każdej wartości energii ho < hokr odpowiadają2głębokości strugi przy tym samym strumieniu (wydatku) objętościowym. Dla dużych h - górna gałąź - ruch spokojny h > hkr, nadkrytycznyDla małych h - dolna gałąź - ruch rwący h < hkr, podkrytyczny

 Znajomć głębości krytnej ważna przy bud kanałów, szcznie ziemnych, gdzie duża pręość niepożąa ze wzgl na wytrzłość podłoża. Spadek krytyczny - spadek dna, przy kt struga płynąca ru jednosm osiąga głębość kryt Odskok hydrauliczny - próg Bidone'a-Przeje r spokoj w rwącPrzejście r rwącego spokojny.uskok-duża strata ene płynącej strugi.Z równania energii

Możliwe jest tylko c2-c1<0, bo nie może być przyrostu energii mechj, a ta enea ulega rozproszeniu w w odskoku hydraunym.Aby obliczyc odskok hydrauny musimy znać:1głebokośćkrytyczną hkr2różnicęwzniesien c1-c2 górnego i dolnego zbiornikaPrzelewy przegrodaustawiona w kanale otwm.

Spiętrzenie wody i przelewanie się jej ponad krawędzią.Także wypływ przez duży otwór, jeśli swobodna powiernia znajduje się na poz lub poniżej górnej krawędzi otworu. Są to zwykle budowle piętrzące, jazy, śluzy, itp.Także układ do pomiaru wydatku cieczy (wody).Przelewy:

1o cienkich ścian2grubszych ścianach3o szerokiej koronie

 

1górne zwierciadło2dolnezwierciadło

3korona, próg, grzbiet.Przelew o cienkiej ściance a) niezatopiony b) zatopionyW zależi od szerci przelewu w stosukanału:

1przelewybez bocznego zwężenia

2zbocznym zwężeniem.Położenie przegrody wzgl kierunku przepływu:

proste, ukośne, boczne, krzywoliniowe

Na kształt prześwitu przegrody:

- prostokątny, - trapezowy, - półokrągły, - trójkątny Przelew o cienkich ściankach

Elementarny wydatek

Prędkość

współcznn przelewu

αo=0.60÷0.64

Przelew zatopiony Warunki:

- próg powinien leżeć poniżej dolnego zwierciadła wody,spełnionanierówność h1 /H1 < 0,75Jeśli pierwszy warunek nie spełny to zawsze będzie przelew niezatopi.

Pierwszy spełniony, a drugi nie - przelew niezatop z odskokiem hydraulicznym.

 Wydatek objętościowy

ၡ1 = ၡ2 = 0,633

ၳ - współczynnik zatopienia

Przelew o grubych ściankach

Przelew niezatopiony, linia ciągła, próg przelewu powyżej dolnego zwierciadła

Linia przer - przepływ zatopiony, korona poniżej zwierciadła dolnego

ၡ = 0,83przelewy opływowe= 0,60 przelewy nieopływowealfa zal od kszta orony przelewu

Przelew o szerokiej koronie

Odskok hydrauliczny Obserw dla Fr > 1 w przepłch z prędkościami nadkrytycymi.

Efekty dyssypacji, dyspersji, nieliniowe i napięcie powierzwe wpływają na strukrę przepłu w obszarze odskoku. Rów zachnia pędup1 = po + ၲ g (h1 - z) w kierunku pionowymp2 = po + ၲ g (h2 - z)

W kierunku poziomym

Rów zachowania energii

Dla Fr = 1 h2 = h1(nie ma odskoku)

Dla Fr > 1 h2/h1>1

Dla Fr < 1 h2/h1<1

Z równ zacha energii obly różnicę en wew

dla Fr1 > 1 jest zawsze Fr2 < 1

Przepływ za odskokiem jest zawsze przepływem z prędkością podkrytną, a więc spokojnym. Przyrost enewewnę w odskokue2 > e1 jest związany z silnymi procesami dyssypatywnymi w odskoku.

 dla Fr = 1 Ⴘ 1,8 silniejsze są efekty dyspersji. W tym przypadku wyst odskok zafalowany tzw. bor. Dopiero dla większych liczb Froude'a Fr załamuje się czoło fali i zaczyna się formować odskok hydrauny z silną dyssypacją energii.

Odskok hydrauliczny można wykorzystać do:Rozpraszania energii strumieniaPodniesienia poziomu cieczy

Wymieszania dodatku do cieczy

Napowietrzania cieczy

 Silne stacjonarne odskoki hydliczne są analogiem fal uderzeniowych w gazodynamice i mogą być wyk do badań analogowych przepływu gazu.Przepływy w kana zamkn Najprostszy przewód - przewód pojedynczy, może być prostolini lub zagięty, o stałym lub zmiennprzekroju, leżeć w jednej płaszczyźnie lub nie.

Dla przepływu stacjonarnego - wydatek w każd przekroju jednakowy.Zadprzy oblic przepływu przez kanał:Oblicz naporu, przy kt wydatek cieczy w przewodzie osiągnie z góryzadanąartość (wymiary kanału zadane)Obli wydatku przy zadanym naporze i wymiarach kanałuWyznacz wymiarów przewoduNajodpowie

dniejszego na podstawie zadanego kryterium np.. Ekonomicznego

Zadanie 3 odwrotne wzgl dwóch poprzednich

Do wyznacz wydatku Q stosujemy 2metdy:kolejnych przybliżeńwykreślno-rachunkowa Liniapiezometryczna ma mniej regularny kształt niż linia ene

całkowitej. Ciśn może bowiem wzdłuż przewodu rosnąć. Dla cieczy dos linia ene

jest prostą pozi, dla cieczy lepk opada wzdłuż przepływu. Na podstawie linii

piez można wnosić o możliwości pojawienia się np. kawitacji Dwieniewiadome średna d i różnica ciśnń.Pompa - różnica ciśnień, zal od projektanta, przewód i jego ułożee są tym

tańsze im mniejsza średnica przewodu, jeśli średnica przewodu maleje,

rośnie różnica ciśnień. Wtedy koszt pompy i jej eksploai będą odpowiednio

wyższe, powięksie przewodu daje efekt odwrotny: koszt rurociągu i jego ułożenie wzrośnie, a koszt pompy i jej eksploatacji zmaleje. Należy znaleźć zatem średnicę ekonomiczną. Zwykle na podste wykresu:

Ukłprzewodów albo rurociąg złożony- zesp kanałów (przewodów) połący

ze sobą węzłach.Oblicz ukł przewodów opiera się na pokazanych równ dla pojedynczychprzewodów z uwzgl warunków węzłach. Tzn.:Suma wydatków doprowadc do węzła jest =sumiewydatków

odprowadzonychEne całkowi każdej strugi jest w węźle jednako ( w przybli).

Rozgałęzienie przewodów1jednym dopływa dwoma odpływa2dwomadopływa jednym odpływa

Atmosfera ziemska3modele atmosfery:

1. Jednorodnaၲ = ၲo = const Stosowany przy małych różnicach wysokości w dowolnej warstwie atmosfery

2. Izotermiczna: T = const

3. Liniowy spadek temperatury z wysokością: T ~ z.W toposferze, gdzie mamy liniowy spade temp

Z równania statyki

otrzymamy

 Równa to można scałkować dla: ၲ = ၲ(p)płyn barotropowyၲ = ၲ(p, z)f ciś i wysokościJednorodna

tzw. wysok atmos jednorj, czyli granica atmosf zieiej, gdyby jej gęstć była stała i równa ၲoIzotermiczna:

temp T1 = To odpowiada wysokości z1

Jest to wzór barometrycznyAtm o liniom spau temp Powietrze - gaz doskonały

Zakładamy, że temp zmienia się liniowoT = To - ၬ zZleżność pomiędzy ciś a gęstą jest politropą.

Atmos wzorcowa - oparta o model atmosf izotermic i o liniowym spadku temp z wysokością Powietrze jest gazem doskon,

temper maleje liniowo do - 56,5oC przy ၬ = 0,0065 o K/mi stała temp w izosferze

Atmo ziemska jest bardzo niejednolita

 Param opisujące atmoę zmieniają się z odległo od powierzchni Ziemi jak i w czasie,- temp- skł chem- ciś- ład lektryczny- gęstość- droga swobo cząsteczek gazów tworzących atmos

 Temper i ciśe atmos decydują o równow i stateczn atmoyTroposfera 8 Ⴘ 17 km - liniowy spadek temp z wysokzjawis pogodotwóe, chmury, opady, silne przemiese, dlat skł chemi troposfery jest praktycznie niezależny od wysokości.

Rozkład tempey w troposferze zależy od pory roku i dnia, może wystąpić też inwersja czyli wzrost temp z wysok.

 Stratosfera do ostatniego lokalnego minimum na wysokości 80 km

podstrefy - izosfera - stała temp, nie ma tu piono ruchów powietrza, szybkie wiatry poziome 500 km/hSkł chemiy nie jest stały 15 Ⴘ 50 km znaczne ilości ozonu maxna wysoko 25 km.Termosfera - liniowy wzrost temp do bardzo duży wartości do ~2000oCEgzosfera - cząstki gazu poruszają się już bardzo swobodnie jako miniat ciała niebie Założenia kinetyc teorii gazów niespełnione, pojęcie temp traci sens. stateczność atmosfery zależy od gradientu tempe.

၄ = 0,98oK/100 mdla powietrza, adiabata

Inwersja - wystę zwyk nad ranem w zw z ochłodz się nisko zalegh warstw powia wskutek konta z szybko stygnącą powierz ziemi. Po nagrzaniu się powierzi ziemi w ciągu dnia, jak atmosf staje się niestateczna, pojawiają się prądy pione w atmosf, kt nasilenie obserwuje się szczege w godz połudh.

Ode

rwanie przepływu nastąpi w przypadku 2 a), czyli jako obszar z ujemną prędkością u(y)

Podstawowa różnica Podstawowa różnica:

Podstawowa różnica:

---
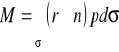
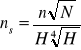
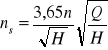
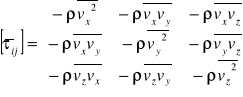
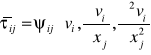
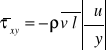
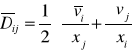
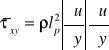
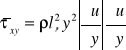
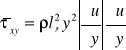
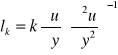
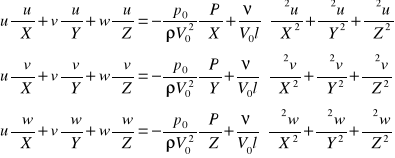
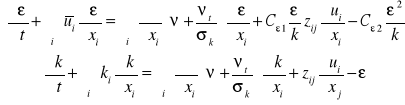
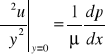
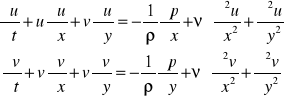
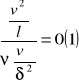
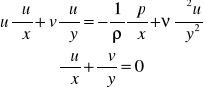
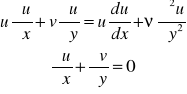
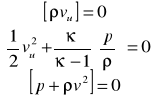
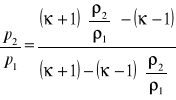
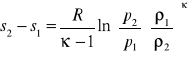
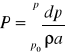
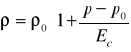
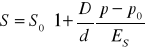
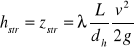
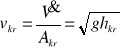
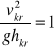
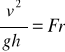
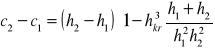
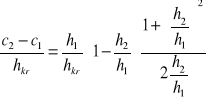
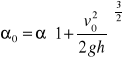
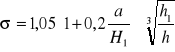
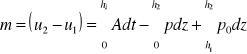
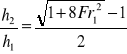
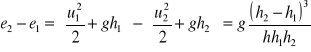
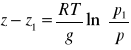