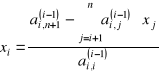UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
Oznaczenia:
![]()
- macierz współczynników układu, ![]()
- wektor niewiadomych, ![]()
- wektor wyrazów wolnych
Układ ![]()
-równań, ![]()
-niewiadomych
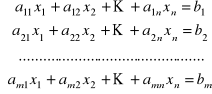
Postać macierzowa: ![]()
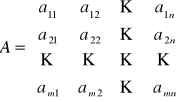
, 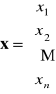
, 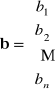
Metoda eliminacji Gaussa
Uwaga 1: ![]()
(liczba równań = liczbie niewiadomych)
Uwaga 2: działamy tylko na wierszach!!!
Układ równań w postaci: ![]()
,
gdzie
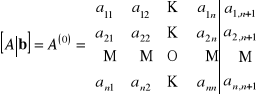
,
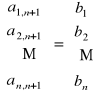
Metoda polega na przekształcaniu macierzy ![]()
tak, żeby macierz współczynników układu ![]()
była macierzą trójkątną górną (pod główną przekątną zera, ![]()
- elementy na głównej przekątnej dla ![]()
):
zerowanie elementów w
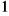
-ej kolumnie pod główną przekątną
dla
![]()
![]()
(żeby wyzerować elementy w pierwszej kolumnie mnoży się pierwszy wiersz przez stałą ![]()
i dodaje do niego elementy ![]()
-ego wiersza, ![]()
)
![]()
![]()
zerowanie elementów w
-ej kolumnie pod główną przekątną
dla
![]()
![]()
(żeby wyzerować elementy w drugiej kolumnie mnoży się drugi wiersz przez stałą ![]()
i dodaje do niego elementy![]()
-ego wiersza, ![]()
)
![]()
![]()
zerowanie elementów w k-ej kolumnie pod główną przekątną
dla ![]()
, ![]()
, ![]()
(żeby wyzerować elementy w ![]()
-ej kolumnie mnoży się![]()
-ty wiersz przez stałą ![]()
i dodaje do niego elementy![]()
-ego wiersza, ![]()
)
![]()
![]()
Postępowanie wsteczne - wyznaczenie rozwiązania układu równań ![]()
(z postaci ![]()
):
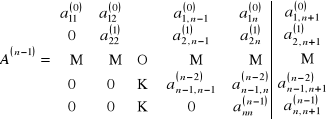
![]()
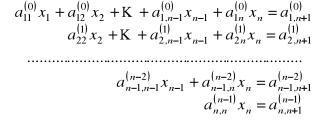
Wyznaczenie niewiadomej
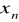
z ostatniego równania
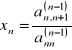
Wyznaczenie niewiadomej
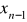
z przedostatniego równania
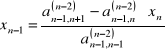
Wyznaczenie niewiadomej
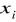
z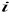
-go równania (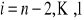
)