![]()
, (1)
Celem ćwiczenia jest:
Sprawdzenie zależności teoretycznej indukcji magnetycznej solenoidu B w funkcji prądu I.
Sprawdzenie zależności teoretycznej indukcji magnetycznej solenoidu B w funkcji gęstości liniowej zwojów solenoidu n.
Wyznaczenie przenikalności magnetycznej próżni μ0.
Zgodnie z prawem Biota-Savarta, wektor pola magnetycznego B w punkcie P, generowanego przez przewodnik, z płynącym prądem I, podaje się w postaci sumy (całki) odpowiednich udziałów cząstkowych dB, pochodzących od odcinków przewodnika o długości wektorowej ds
![]()
, (1)
gdzie ![]()
jest przenikalnością magnetyczną próżni, a r to długość wektora r skierowanego od danego elementu ds przewodnika do punktu P. Obliczenie całkowitej wartości pola magnetycznego wymaga całkowania zależności (1). W wielu przypadkach obliczanie takiej całki jest bardzo skomplikowane i tylko dla cewek o prostych kształtach wyznaczane są postaci analityczne wzorów. W niektórych sytuacjach np., kiedy jest obliczane pole magnetyczne cewki długiej (solenoidu) lepiej jest zastosować prawo Ampera, które może być otrzymane z prawa Maxwella
![]()
, (2)
gdzie j- gęstość prądu, IA - prąd płynący przez powierzchnię A, która jest ograniczona zamkniętą krzywą S.
Rys. 1. Linie pola magnetycznego cewki długiej
Aby policzyć pole magnetyczne cewki długiej wybrano powierzchnię A i krzywą S jak na rysunku 1. Cewka jest na tyle długa, że wektor pola magnetycznego B wewnątrz jest równoległy do osi cewki a na zewnątrz cewki wartość wektora B jest znikoma. To oznacza, że tylko w części S1 o długości L krzywej całkowania S wartość odpowiedniej całki (2) nie będzie równa zeru.
![]()
. (3)
Wewnątrz krzywej całkowania S jest N zwojów cewki, a więc prąd IA płynący przez powierzchnię A ograniczoną krzywą S równy jest:
![]()
(4)
Ostatecznie indukcja pola magnetycznego wewnątrz solenoidu wynosi:
![]()
(5)
gdzie I to prąd płynący przez cewkę, a n to gęstość liniowa zwojów na jednostkę długości solenoidu (N/L).
W czasie eksperymentów będzie mierzone pole magnetyczne solenoidu B. Do tego celu zastosowany zostanie detektor indukcji magnetycznej, umieszczony w osi solenoidu. Detektor zbudowany jest na bazie czujnika Halla, czułego na pole magnetyczne, wektor którego jest skierowany wzdłuż osi detektora.
Ocena dokładności pojedynczych pomiarów:
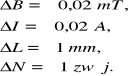
Tabela danych doświadczalnych:
|
L = 30,7 cm |
|
|
|
|
|
|||||||
I [A] |
Bśr [mT] |
∆Bśr [mT] |
Bteor [mT] |
- k |
∆k |
μ0i |
∆μ0i |
|
|||||
20 |
-2,455 |
0,055 |
-2,456 |
-1,228·10-4 |
2,627·10-6 |
1,256·10-6 |
4,993·10-8 |
|
|||||
18 |
-2,260 |
0,070 |
-2,210 |
-1,256·10-4 |
3,749·10-6 |
1,285·10-6 |
5,765·10-8 |
|
|||||
16 |
-1,990 |
0,040 |
-1,965 |
-1,244·10-4 |
2,345·10-6 |
1,273·10-6 |
4,892·10-8 |
|
|||||
14 |
-1,800 |
0,040 |
-1,719 |
-1,286·10-4 |
2,673·10-6 |
1,316·10-6 |
5,187·10-8 |
|
|||||
12 |
-1,525 |
0,035 |
-1,474 |
-1,271·10-4 |
2,705·10-6 |
1,300·10-6 |
5,161·10-8 |
|
|||||
10 |
-1,265 |
0,045 |
-1,228 |
-1,265·10-4 |
4,247·10-6 |
1,295·10-6 |
6,139·10-8 |
|
|||||
8 |
-1,075 |
0,035 |
-0,982 |
-1,344·10-4 |
4,039·10-6 |
1,375·10-6 |
6,188·10-8 |
|
|||||
6 |
-0,790 |
0,030 |
-0,737 |
-1,317·10-4 |
4,561·10-6 |
1,347·10-6 |
6,492·10-8 |
|
|||||
4 |
-0,595 |
0,035 |
-0,491 |
-1,488·10-4 |
8,006·10-6 |
1,522·10-6 |
9,650·10-8 |
|
|||||
2 |
-0,245 |
0,035 |
-0,246 |
-1,225·10-4 |
0,163·10-6 |
1,254·10-6 |
0,172·10-8 |
|
|||||
-2 |
0,295 |
0,035 |
0,246 |
-1,475·10-4 |
0,160·10-6 |
1,509·10-6 |
0,172·10-8 |
|
|||||
-4 |
0,555 |
0,055 |
0,491 |
-1,388·10-4 |
0,131·10-6 |
1,420·10-6 |
0,142·10-8 |
|
|||||
-6 |
0,850 |
0,050 |
0,737 |
-1,417·10-4 |
7,861·10-6 |
1,450·10-6 |
9,396·10-8 |
|
|||||
-8 |
1,115 |
0,055 |
0,982 |
-1,394·10-4 |
6,527·10-6 |
1,426·10-6 |
8,211·10-8 |
|
|||||
-10 |
1,325 |
0,055 |
1,228 |
-1,325·10-4 |
5,235·10-6 |
1,356·10-6 |
7,023·10-8 |
|
|||||
-12 |
1,580 |
0,050 |
1,474 |
-1,317·10-4 |
3,947·10-6 |
1,347·10-6 |
6,056·10-8 |
|
|||||
-14 |
1,845 |
0,055 |
1,719 |
-1,318·10-4 |
3,740·10-6 |
1,349·10-6 |
5,920·10-8 |
|
|||||
-16 |
2,120 |
0,050 |
1,965 |
-1,325·10-4 |
2,959·10-6 |
1,356·10-6 |
5,458·10-8 |
|
|||||
-18 |
2,455 |
0,065 |
2,210 |
-1,364·10-4 |
3,460·10-6 |
1,396·10-6 |
5,864·10-8 |
|
|||||
-20 |
2,675 |
0,055 |
2,456 |
-1,338·10-4 |
2,616·10-6 |
1,369·10-6 |
5,309·10-8 |
|
|||||
Do wyznaczenia linii trendu postaci B = a·I + b użyjemy metody najmniejszych kwadratów, tj. zastosujemy wzory:
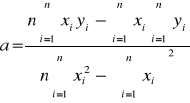
oraz
![]()
.
Mamy stąd
![]()
Zestawienie danych w postaci wykresu:
Odchylenie standardowe może służyć jako miara niepewności. W fizycznym sensie odchylenie standardowe dla grupy powtarzanych pomiarów daje obraz precyzji pomiaru. Kiedy trzeba zdecydować, czy pomiary zgadzają się z teoretycznymi przewidywaniami, ich odchylenie standardowe nabiera kluczowej roli: Jeśli średnia z pomiarów jest zbyt daleko od wartości przewidywanej (przy czym odchylenie standardowe służy tu za jednostkę pomiaru tej odległości), uważa się, że pomiary zaprzeczają przewidywaniom. Oznacza to bowiem, że wypadają one poza zakres wartości, który można by zdroworozsądkowo uznać za prawdopodobny, jeśli przewidywania były słuszne.
Odchylenia standardowe współczynników - k i ∆k to:
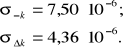
Co oznacza, że pomiary są zbliżone do wartości teoretycznych, co z kolei świadczy o dokładności przeprowadzonego eksperymentu.
Wartości μ0i oraz ∆μ0i zostały obliczone i przedstawione w tabeli znajdującej się powyżej.
Średnia wartość przenikalności magnetycznej próżni otrzymanej w doświadczeniu to
![]()
, natomiast wartość teoretyczna to ![]()
,
różnica pomiędzy wartościami wynosi zatem ![]()
.