4. Prognozowanie na podstawie modelu ekonometrycznego

4.1 Podstawy teoretyczne

Załóżmy, że rozpatrujemy statyczny, liniowy model ekonometryczny, zapisany w skalarnej postaci jako:

,
.

Składniki zakłócające tego modelu, jak zakładamy, spełniają założenia klasycznego modelu linowego, w tym sensie, że:

;
;
;

,

co odczytujemy, że realizacje składników zakłócających oscylują wokół zera, mają stałe wariancje, są nieskorelowane w czasie, są nieskorelowane ze zmiennymi objaśniającymi oraz mają rozkłady normalne.

Zapisem macierzowym tego modelu jest:

gdzie występujące w tym zapisie wektory mają wymiary odpowiednio:

• wektor obserwacji zmiennej endogenicznej
  -
  ,

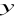
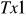
• macierz obserwacji zmiennych objaśniających
  -
  ,

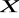
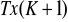
• wektor parametrów strukturalnych
  -
  ,

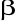
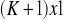
• wektor składników zakłócających
  -
  .

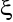
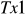
Parametry modelu zapisanego wyżej są szacowane, zwykle metodą najmniejszych kwadratów, zgodnie z:

;
,

gdzie
jest
wymiarową macierzą wariancji-kowariancji błędów estymacji.

Kolejnym etapem procedury budowy modelu jest jego weryfikacja. Procedura weryfikacji obejmuje zwykle interpretację parametrów strukturalnych, ocenę dobroci dopasowania modelu oraz testowanie wybranych hipotez statystycznych dotyczących w szczególności: indywidualnych parametrów strukturalnych (tzw. indywidualne hipotezy istotności), parametrów rozkładu składników zakłócających (stałości wariancji, braku skorelowania w czasie) oraz postaci funkcji gęstości rozkładu składników zakłócających (testowanie normalności rozkładu).

Kluczowym założeniem, umożliwiającym wykorzystanie oszacowanego modelu ekonometrycznego jako narzędzia prognozowania jest założenie o stałości w czasie mechanizmu generowania obserwacji. Zakładamy zatem, że model zdefiniowany dla okresów próbkowych
, jest aktualny dla okresów pozapróbkowych (prognozowanych)
. W szczególności okres ten może być, choć nie musi być, okresem przyszłym, dla którego realizacje zmiennych modelu nie są znane. Przy spełnieniu założenia aktualności modelu, które będzie przedmiotem weryfikacji w trakcie dalszych części wykładu, możemy zapisać, że dla założonych wartości zmiennych egzogenicznych w okresie
, modelem generującym pozapróbkowe realizacje zmiennej endogenicznej jest:

,

gdzie
jest składnikiem zakłócającym w okresie prognozowanym. Założenie aktualności modelu, w węższym zakresie, interpretujemy nie tylko jako stałość w czasie parametrów strukturalnych modelu lecz również jak stałość parametrów rozkładu składników zakłócających w okresach pozapróbkowych, co zapisywać będziemy:

;
;
;
;
.

Ponadto zakładać będziemy, że składniki zakłócające z okresów prognozowanych są nieskorelowane ze składnikami okresów próbkowych:

.

Zmienną
, o czym mówiliśmy już w trakcie wykładów poprzednich, nazywamy zmienną prognozowaną. Zmienne objaśniające w okresach pozapróbkowych (
) natomiast, nazywać będziemy zmiennymi prognozującymi. Wprowadzając oznaczenie:

dla 1x(K+1) wymiarowego wektora zmiennych prognozujących, zapiszemy zmienną prognozowaną w następujący sposób:

.

Z punktu widzenia prognozowania ważne będzie rozróżnienie dwóch przypadków. Przypadek pierwszy, gdy wartości zmiennych objaśniających w okresach pozapróbkowych są znane i drugi, gdy wartości tych zmiennych nie są znane. Przypadek pierwszy dotyczy sytuacji, gdy zmienna endogeniczna (prognozowana) jest wyjaśniana przez zmienną czasową, funkcje zmiennej czasowej, zmienne periodyczne (zero-jedynkowe lub trygonometryczne) lub opóźnione zmienne endogeniczne. Przypadek drugi obejmuje wszystkie inne sytuacje.

Modele o znanych pozapróbkowych wartościach zmiennych objaśniających są najbardziej naturalnymi narzędziami prognostycznymi. Umożliwiają bowiem wyznaczenie prognoz bezwarunkowych w warunkach stabilności w czasie modelu. Modele pozostałe pozwalają w ogólnym przypadku na wyznaczanie prognoz warunkowych, typu ,,jeżeli to''. Prognozy te, jak pokażemy na przykładach, zależą od wartości jakie przyjmiemy dla zmiennych objaśniających na okresy prognozowane.

W tablicach 1a-1b podajemy skalarny i macierzowy zapis modelu w warunkach stabilności w czasie.

Tablica 1a. Model ekonometryczny w warunkach stabilności (zapis skalarny)

Okresy historyczne (t)	Okresy prognozowane (T+j)

Tablica 1b. Model ekonometryczny w warunkach stabilności (zapis macierzowy)

Okresy historyczne (t)	Okresy prognozowane (T+j)

Jeśli przyjęte założenia są prawdziwe, co będzie przedmiotem weryfikacji dalszych częściach wykładu, możemy obliczyć oczekiwaną wartość zmiennej prognozowanej w następujący sposób:

.

Jeśli zmienne prognozując w wektorze mają znane i ustalone wartości, wtedy
. Najprostszym przykładem jest model trendu deterministycznego, w którym składnik systematyczny zmiennej endogenicznej jest opisywany za pomocą deterministycznej funkcji czasu. Jeśli wartości zmiennych objaśniających w okresach pozapróbkowych nie są znane, wtedy
interpretować będziemy jako wektor ustalonych wartości zmiennych prognozujących., zaś oczekiwana wartość zmiennej endogenicznej będzie warunkowa względem przyjętych wartości dla zmiennych prognozujących.

Oczekiwana wartość zmiennej endogenicznej jest nieznanym parametrem rozkładu zmiennej prognozowanej. Jest wyznaczona jako kombinacja liniowa zmiennych prognozujących, gdzie współczynnikami tej kombinacji są parametry strukturalne modelu. Prognozę zmiennej
, wyznaczoną w okresie
, nazywać będziemy estymator oczekiwanej wartości zmiennej endogenicznej warunkach aktualności modelu próbkowego. Napiszemy zatem, że:

lub skalarnie jako:

.

W dalszej części wykładu nie będziemy wykorzystywać oznaczenia
, używając skrótowego zapisu
, pamiętając wszakże o tym, iż prognoza jest wyznaczona na podstawie próbkowych
obserwacji , na pozapróbkowy okres
. Prognozę wyznaczoną w taki sposób nazywamy prognozą ekstrapolacyjną, gdyż oceny parametrów uzyskane na podstawie informacji historycznych (próbkowych) SA wykorzystane w oszacowaniu pozapróbkowej wartości oczekiwanej.

Jeśli w prognozowaniu wykorzystywany jest estymator MNK parametrów, tj.
, wtedy prognozę:

nazywamy prognozą MNK.

Błąd prognozy ex ante w warunkach stabilności modelu zapisać można jako:

.

Błąd ten jest nieobserwowany, dopóki nie jest znana realizacja zmiennej prognozowanej
. Błąd ten zawiera dwa składniki, mianowicie:

oraz

.

Składniki te objaśniają jednocześnie przyczyny błędów prognoz, wyznaczanych przy pomocy modelu ekonometrycznego. Przyczyną pierwszą jest losowy mechanizm generowania zmiennej prognozowanej (endogenicznej). Jego wynikiem jest występowanie odchyleń pomiędzy zrealizowaną, a oczekiwaną wartością zmiennej endogenicznej. Z drugiej strony, na skutek błędów popełnionych w estymacji parametrów modelu, oszacowanie oczekiwanej wartości zmiennej prognozowanej jest obarczone błędem. Gdyby nawet błędy estymacji były zerowe, tj. gdybyśmy dysponowali idealnym narzędziem prognozowania, popełnialibyśmy błąd prognozowania równy
. Zatem, jeżeli
, to
.

Jeżeli przyjęte założenia odnośnie do rozkładu składników zakłócających są prawdziwe, to prognoza MNK wyznaczona jako
, nazywana jest prognozą nieobciążoną, w tym sensie, że:

lub

.

Wariancją błędu prognozy ex ante, w warunkach prawdziwości założenia o aktualności modelu, jest:

.

gdzie
jest macierzą wariancji-kowariancji błędów estymacji MNK.

Oznaczając wariancje błędów estymacji poszczególnych parametrów, tj. elementy na głównej przekątnej macierzy
jako
, natomiast kowariancje błędów estymacji, tj. elementy poza główną przekątną macierzy
jako
, wariancję błędu prognozy zapiszemy w następujący sposób:

.

Wariancja błędu prognozy jest średnim kwadratowym odchyleniem zmiennej prognozowanej od prognozy. W przypadku, gdy wartości zmiennych prognozowanych w okresie
nie są znane, ale przyjęte przez prognostyka, wtedy wariancja błędu prognozy, tak jak prognoza ma interpretację warunkową, dla założonych wartości czynników prognozujących. Wariancja jest zatem miarą ryzyka zrealizowania się zmiennej prognozowanej na poziomie odbiegającym od prognozy.

Pierwiastek z wariancji nazywamy średnim błędem prognozy ex ante:

Błąd ten określa przeciętne in plus, in minus odchylenie zmiennej prognozowanej od prognozy.

Próbkowe oceny wariancji błędu prognozy oraz średniego błędu prognozy znajdziemy wykorzystując wariancję reszt. Zapiszemy zatem:

,

gdzie
jest estymowaną (próbkową) macierzą wariancji-kowariancji błędów estymacji MNK oraz

.

Wariancja błędu prognozy oraz średni błąd prognozy są absolutnymi miarami ryzyka, zależnymi od jednostek w jakich wyrażona jest zmienna prognozowana. Dlatego, do oceny dokładności prognozy wykorzystuje się zwykle relatywną miarę ryzyka, nazywaną względnym błędem prognozy
i definiowaną jako:

.

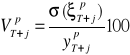
Jej empirycznym odpowiednikiem jest:

.

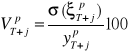
Określa on jaki procent wartości prognozy stanowi jej średni błąd. Miara ta jest wykorzystana jako kryterium dopuszczalności prognozy.

Rozważmy iloraz błędu prognozy, przez średni błąd prognozy. Jeśli składniki zakłócające mają rozkłady normalne, to iloraz ten ma rozkład t-studenta o
stopniach swobody. Możemy zapisać, że:

.

Prawdopodobieństwo otrzymania realizacji typowej dla tego rozkładu, tj. bliskiej zeru jest bliskie jedności, co zapisujemy:

,

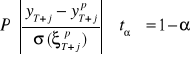
natomiast prawdopodobieństwo otrzymania realizacji tego ilorazu daleko odbiegającego od zera jest bliskie zeru, tj:

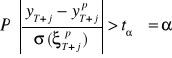
gdzie
jest wartością krytyczną z rozkładu t-Studenta, natomiast
jest bliskim zera, akceptowanym przez badacza, poziomem ryzyka.

W konsekwencji możemy zapisać, że kolejno:

,

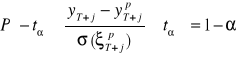
oraz

.

Dla założonych wartości czynników prognozujących, przedział ten z prawdopodobieństwem
, pokrywa nieznaną realizację zmiennej prognozowanej. Rozpiętość tego przedziału zależy od dwóch czynników:

• dokładności prognozowania (średniego błędu prognozy ex ante),

• przyjętego poziomu ryzyka wnioskowania.

Jest zrozumiałe, że większy średni błąd prognozy, przy przyjętym poziomie ryzyka, powodować będzie rozszerzanie się granic przedziału ufności. Z drugiej strony, dla danego poziomu średniego błędu prognozy, przedział ufności może być rozszerzony, gdy przyjmujemy mniejsze ryzyko lub zwężony, gdy akceptujemy większe ryzyko.

4.2 Prognoza na podatnie modelu liniowej tendencji rozwojowej

W najprostszej sytuacji szereg czasowy
zawiera dwie składowe, mianowicie składową systematyczną oraz nieregularną (przypadkową), które są addytywne. Model takiego szeregu czasowego zapiszemy w postaci:

;

gdzie:
- deterministyczna funkcja opisująca zmiany systematyczne,
- losowy składnik zakłócający.

Metody wyboru funkcji opisującej zmiany systematyczne szeregu są różne. Najczęściej stosowane są metody graficzne i analityczne (ekonometryczne). Metody graficzne polegają na analizie wykresów szeregów czasowych i doborze względnie postaci analitycznej funkcji o znanym przebiegu zmienności. Metody analityczne polegają na testowaniu różnych postaci funkcji przy pomocy wybranych narzędzi ekonometrycznych (ocena dobroci dopasowania różnych postaci modelu, ocena istotności parametrów, ocena stabilności parametrów, testowanie hipotez odnośnie do składników zakłócających) i wyborze takiej postaci empirycznej, która w najlepszy sposób spełnia kryteria przyjęte prze badacza.

Rozważmy model liniowej tendencji rozwojowej, w którym składnik systematyczny jest przedstawiony jako liniowa funkcja zmiennej czasowej:

,

gdzie
,
są nieznanymi parametrami. Parametr
oznacza zatem stały w czasie przyrost składnika systematycznego

Model ekonometryczny szeregu czasowego z liniowym trendem zapiszemy więc w postaci:

.

O składniku zakłócającym tego modelu zakładamy, że spełnia on klasyczne założenia definiujące sferyczne zmienne losowe o rozkładzie normalnym. Założenia te wymieniono w punkcie poprzednim.

Model taki, z uwagi na swoją konstrukcję ma zastosowanie ograniczone do przypadków szeregów czasowych charakteryzujących się inercją oraz niewystępowaniem punktów zwrotnych. W innych przypadkach, po oszacowaniu modelu, testy diagnostyczne wykazywać będą występowanie autokorelacji reszt (w szczególności dodatniej), brak normalności rozkładu reszt oraz zmienną wariancję reszt.

Parametry modelu szacowane są metodą najmniejszych kwadratów. Wykorzystując znane wzory na sumy szeregów zmiennej czasowej oraz kwadratów zmiennej czasowej możemy podać dość proste, skalarne wzory na oszacowania tych parametrów oraz wariancje i kowariancje błędów tych oszacowań:

,

,

,

,

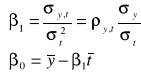
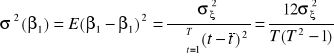
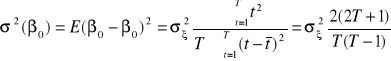
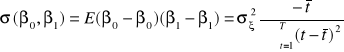
gdzie
jest wariancją reszt z oszacowania modelu.

W konsekwencji oszacowaną postacią modelu trendu liniowego jest:

,

gdzie
jest średnim błędem szacunku odpowiedniego parametru strukturalnego.

Ocenę dobroci dopasowania oraz testowanie hipotez statystycznych przeprowadza się zgodnie ze standardami wyznaczonymi przez program komputerowy wykorzystywany w szacowaniu modelu (np. Statistica, Microfit lub inne). W drugiej części wykładu omawiając przykład empiryczny przypomnimy taką standardową weryfikację modelu.

Załóżmy obecnie, że oszacowany model liniowej tendencji rozwojowej chcemy wykorzystać do wyznaczenia prognozy zmiennej endogenicznej na pozapróbkowy okres
. W klasycznej sytuacji prognostycznej jest to oczywiście okres przyszły (prognozowany), z którego realizacja zmiennej
jest w chwili wyznaczania prognozy niedostępna.

Kluczowym pytaniem na jakie należy odpowiedzieć, by móc rozsądnie wykorzystywać oszacowany model próbkowy do wyznaczania prognozy jest pytanie czy model jest stabilny prognostycznie. Problem ten może być analizowany w różny sposób. Poświęcamy mu odrębny wykład. Obecnie zakładamy, że model jest aktualny w okresach pozapróbkowych. Przy tym założeniu możemy zapisać, że:

,

gdzie
jest zakłóceniem losowym w okresie
, spełniającym założenia takie jak w okresach próby.

Wykorzystując wygodny zapis macierzowy otrzymamy:

gdzie:
jest wektorem
wymiarowym, natomiast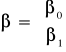
jest wektorem parametrów o wymiarach
.

W warunkach, gdy przyjęte założenia są prawdziwe, oczekiwana wartość zmiennej prognozowanej zapisuje się jako:

.

Powyższe wyrażenie należy interpretować jako składnik systematyczny w okresie prognozowanym, tj.;

.

Prognozą
nazywać będziemy estymator oczekiwanej wartości zmiennej prognozowanej na okres
:

lub w tożsamym zapisie macierzowym:

.

Zapis powyższy oznacza, że wyznaczając ocenę oczekiwanej wartości na okres
wykorzystaliśmy próbkowe oceny parametrów strukturalnych modelu. Jest to zatem równoznaczne z ekstrapolacją modelu próbkowego na okres
.

Błąd prognozy ex ante
, w omawianym przez nas przypadku ma postać:

.

Jeśli spełnione są założenia stochastyczne modelu, wtedy prognoza MNK nie jest obciążona systematycznym błędem, tj.:

.

Wariancja błędu
w omawianym obecnie przypadku ma postać:

,

jej empirycznym odpowiednikiem jest:

.

Przykład

W tablicy 1 przedstawione są oszacowania modelu liniowej tendencji rozwojowej, uzyskane MNK. Zmienną endogeniczną jest tutaj kwartalna stopa inflacji
w Polsce, obserwowana w kolejnych kwartałach 1999Q1-2002Q4, zatem dla
.

Tablica 1. Ordinary Least Squares Estimation

*******************************************************************************

Dependent variable is y

16 observations used for estimation from 1999Q1 to 2002Q4

*******************************************************************************

Regressor Coefficient Standard Error T-Ratio[Prob]

C 3.0325 .43033 7.0470[.000]

t -.19059 .044503 -4.2826[.001]

*******************************************************************************

R-Squared .56710 R-Bar-Squared .53618

S.E. of Regression .82060 F-stat. F( 1, 14) 18.3404[.001]

Mean of Dependent Variable 1.4125 S.D. of Dependent Variable 1.2049

Residual Sum of Squares 9.4274 Equation Log-likelihood -18.4713

DW-statistic 1.9758

*******************************************************************************

Diagnostic Tests

*******************************************************************************

* Test Statistics * LM Version * F Version *

*******************************************************************************

* A:Serial Correlation*CHSQ( 4)= 3.1145[.539]*F( 4, 10)= .60427[.668]*

* B:Functional Form *CHSQ( 1)= .97215[.324]*F( 1, 13)= .84097[.376]*

* C:Normality *CHSQ( 2)= .022967[.989]* Not applicable *

* D:Heteroscedasticity*CHSQ( 1)= .93298[.334]*F( 1, 14)= .86690[.368]*

*******************************************************************************

Modelem opisującym zmiany inflacji w Polsce jest:

,
.

Oszacowaną postacią modelu, zapisana na podstawie tablicy 1, jest:

,
.

Wynika z tego, że nieznany parametr
został oszacowany na poziomie
z błędem
, natomiast parametr
oszacowano na poziomie
z błędem
. Można też powiedzieć, że z kwartału na kwartał, przeciętnie rzecz biorąc, stopa inflacji zmniejszała się o
punktu procentowego z błędem
punktu procentowego. Oceny parametrów są obarczone relatywnie małymi błędami, tak że z ryzykiem bliskim zera można odrzucić hipotezy zerowe
oraz
, na rzecz odpowiednich hipotez alternatywnych tj.
oraz
. Świadczą o tym duże co do modułu wartości statystyk t-studenta oraz bliskie zera [Prob], tj. minimalne poziomy istotności, przy których następuje odrzucenie hipotezy zerowej.

W ocenie dobroci dopasowania zwracamy uwagę na wartości jakie przyjmują syntetyczne miary dopasowania:
,
,
,
. Wynika z nich, że:

• 
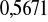
  zmienności inflacji zostało wyjaśnionej przez model liniowej tendencji rozwojowej,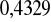

• 
  zmienności stopy inflacji nie zostało wyjaśnionej prze rozpatrywany model,

• wartości zaobserwowane stopy inflacji odchylały się, przeciętnie rzecz biorąc od wartości teoretycznych, wyznaczonych na podstawie modelu tendencji rozwojowej o wartość
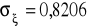
  punktu procentowego,

• średni błąd reszt stanowił około
  średniego poziomu inflacji kwartalnej.

Stwierdzamy zatem, że stopień wyjaśnienia zmienności jest niewystarczający. Zastosowany model jest zbyt prosty do opisu szeregu czasowe inflacji (zob. Rysunek 1).

Oceniając inne aspekty modelu inflacji z tablicy 1, stwierdzamy, że:

• nie występuje istotną autokorelacja składników zakłócających rzędu pierwszego i czwartego, o czym świadczą statystyki
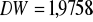
  oraz statystyka Godfrey'a, aby odrzucić hipotezę zerową o nieistotności współczynników autoregresyjnych rzędu do czwartego włącznie trzeba by przyjąć ryzyko wnioskowania nie mniejsze niż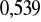
  lub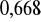
  ,

• nie występuje statystycznie istotna zmienność wariancji składników zakłócających (aby odrzucić hipotezę o stałości wariancji, trzeba zaakceptować ryzyko wnioskowania nie mniejsze niż
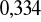
  lub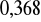
  ,

• składniki zakłócające mają rozkłady nieistotnie odbiegające od normalnego, aby odrzucić tę hipotezę trzeba by przyjąć ryzyko wnioskowania nie mniejsze niż
  

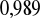
Możemy powiedzieć, że model spełnia podstawowe kryteria weryfikacji.

Z punktu widzenia prognozowania, rozpatrywany model należy ocenić jak zbyt mało dokładny. Odbije się to, jak pokażemy na dokładności prognozowania.

Tablica 2. Single Equation Static Forecasts

*******************************************************************************

Based on OLS regression of y on:

C t

16 observations used for estimation from 1999Q1 to 2002Q4

*******************************************************************************

Observation Actual Prediction Error S.D. of Error

2003Q1 *NONE* -.20750 *NONE* .92659

2003Q2 *NONE* -.39809 *NONE* .94563

2003Q3 *NONE* -.58868 *NONE* .96635

2003Q4 *NONE* -.77926 *NONE* .98863

*******************************************************************************

W tablicy 2 zamieszczono wyniki prognozowania ekstrapolacyjnego na podstawie oszacowanego modelu tendencji rozwojowej. Przy założeniu stabilności modelu prognozy wyznaczono na cztery kwartały w przyszłość, licząc od ostatniego kwartału próby, oznaczonego
. Zatem:

;
.

Prognozy zapisane w tablicy 2, wyznaczono zatem przyjmując, że spadek stopy inflacji, oszacowany na podstawie danych historycznych będzie taki sam w okresach przyszłych.

Prognozy obliczono w następujący sposób:

,
,

,
.

W tablicy 2, w kolumnach ,,Actual'' oraz ,,Error'' znajdujemy oznaczenie *NONE*. Należy to interpretować w następujący sposób: realizacje zmiennej prognozowanej w okresie 2003Q3-2003Q4 nie zostały wprowadzone do bazy danych, są zatem pozapróbkowe. Błąd prognozy ex ante

(error), nie może być wyznaczony, dopóki nie są znane (wprowadzone do bazy danych) realizacje zmiennej prognozowanej (actual). Tym nie mniej, w warunkach stabilności modelu możemy wyznaczyć i oszacować wariancje błędów prognozy ex ante, zgodnie z:

,
.

Elementy empirycznej macierzy wariancji-kowariancji błędów estymacji, które wykorzystywać będziemy w obliczeniach wariancji błędu prognozy ex ante, podane są w tablicy 3.

Tablica 3. Estimated Variance-Covariance Matrix of parameters

*******************************************************************************

Based on OLS regression of y on:

C t

16 observations used for estimation from 1999Q1 to 2002Q4

*******************************************************************************

C t

C .18518 -.016835

t -.016835 .0019805

*******************************************************************************

Podamy obecnie sposób obliczeń wariancji błędów prognoz oraz średnich błędów prognoz ex ante. Dla dwóch pierwszych prognoz w zapisie skalarnym, natomiast dla dwóch ostatnich w równoważnym zapisie macierzowym. Otrzymujemy:

,

,

,

,

,

,

,

.

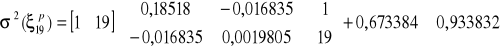
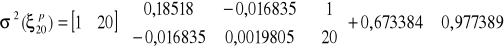
Widzimy zatem, że pomimo iż błędy prognoz są niezaobserwowane, w warunkach założenia o aktualności modelu w okresach przyszłych, możemy wyznaczyć oceny średnich błędów prognoz ex ante.

Możemy obecnie zapisać i zinterpretować wyniki prognozowania, z uwzględnieniem średnich błędów prognoz. Otrzymujemy:

,
,
,
,
,
,

,
.

Oczekujemy zatem, że w okresie 2003Q1 (
) stopa inflacji wyniesie
punktu procentowego, z błędem
punktu procentowego. Inaczej powiedzieć możemy, że zmienna prognozowana odchylać się może od prognozy równej
przeciętnie rzecz biorąc o
. Podobne interpretacje dotyczą pozostałych prognoz.

Obecnie obliczymy względne błędy prognoz ex ante, zgodnie z:

,
.

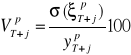
Otrzymamy:

,
,
,

.

W okresie prognozowanym
średni błąd prognozy stanowił około
wartości prognozy na ten okres. W okresie
natomiast średni błąd prognozy stanowił około
wartości prognozy na ten okres. Podobnie interpretuje się pozostałe błędy względne ex ante.

Na koniec utworzymy i zinterpretujemy przedziały ufności dla zmiennych prognozowanych, przyjmując poziom istotności
oraz
. Biorąc pod uwagę liczbę stopni swobody
, wartości krytyczne z rozkładu t-studenta, odpowiadające przyjętym poziomom ryzyka wnioskowania, wyniosą:
oraz
. W konsekwencji dla okresu prognozowanego
zapiszemy:

,

,

,

.

Przedział o końcach
, z prawdopodobieństwem 0,99 pokrywa nieznaną realizację zmiennej prognozowanej. Natomiast przedział
pokrywa realizację zmiennej prognozowanej w okresie
z prawdopodobieństwem 0,95. Widzimy zatem, że mniejszemu ryzyku, któremu odpowiadają wyższe wartości krytyczne, odpowiada szerszy przedział ufności. Jednakże prawdopodobieństwo otrzymania realizacji zmiennej prognozowanej pochodzącej spoza tego przedziału jest mniejsze. Odwrotnie, większemu ryzyku, odpowiadają mniejsze wartości krytyczne. W związku z tym przedział ufności jest węższy, ale prawdopodobieństwo otrzymania realizacji zmiennej prognozowanej spoza tego przedziału jest większe.

Podobnie oblicza się i interpretuje przedziały ufności dla pozostałych okresów prognozowanych.

Aneks 1

Wariancja błędu prognozy ex ante

Błąd prognozy ex ante, w warunkach prawdziwości założenia o aktualności modelu, jest równy:

.

Jeśli spełnione są założenia dotyczące składników zakłócających, wtedy błąd prognozy ma nadzieję równą zero, natomiast jego wariancja jest równa:

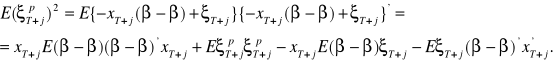
Wyrażenie
definiuje
wymiarową macierz wariancji-kowariancji błędów estymacji. Równość
zachodzi jako wynik braku skorelowania w czasie składników zakłócających próby ze składnikami zakłócającymi okresów prognozowanych. Wyrażenie
definiuje wariancję składników zakłócających. W konsekwencji prawdziwa jest równość:

.

Aneks 2

Rozkład błędu prognozy ex ante w warunkach aktualności modelu ekonometrycznego.

Iloraz błędu prognozy ex ante do średniego błędu prognozy ma rozkład t-studenta, co zapisujemy:

.

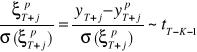
Podzielmy licznik i mianownik ilorazu zapisanego wyżej przez średni błąd prognozy
. W wyniku tego otrzymamy:

.

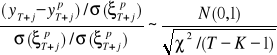
Licznik jest po prostu standaryzowaną zmienną o rozkładzie normalnym, ponieważ błąd prognozy jest liniową funkcją składników zakłócających, zatem ma rozkład normalny:

.

Mianownik jest natomiast zmienną o rozkładzie
, ponieważ:

,
,

zatem

.

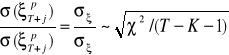
Średni błąd reszt, jest pierwiastkiem z wariancji reszt. Wariancja reszt jest natomiast obliczana jako suma kwadratów reszt podzielona przez liczbę stopni swobody. Jeśli zatem składniki zakłócające mają rozkłady normalne, to kwadraty zmiennych o rozkładzie normalnym mają rozkłady
. Zachodzi zatem:

.

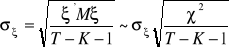
W konsekwencji prawdziwy jest wynik, zapisany na początku aneksu, gdyż rozkład ilorazu niezależnych zmiennych o rozkładzie normalnym i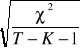
daje zmienna o rozkładzie o t-studenta.

Aneks 3

Estymator MNK dla modelu trendu liniowego

Niech modelem szeregu czasowego
będzie:

.

W zapisie macierzowym
występują zapisane niżej macierze i wektory:

;
;
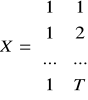
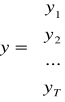
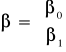
odpowiednio o wymiarach:
;
oraz
.

Estymator MNK parametrów tego modelu
otrzymywany jest jako rozwiązanie układu równań normalnych
. Można pokazać, że macierz
spełnia:

.

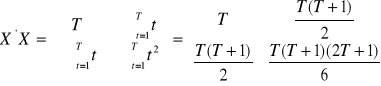
Wyznacznikiem tej macierzy jest
, w związku z tym macierzą odwrotną do
jest:

,

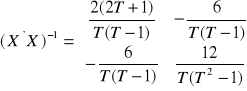
natomiast wektorem
jest:

.

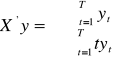
Z powyższych wzorów wynika że, średnia arytmetyczna zmiennej czasowej
, natomiast wariancja zmiennej czasowej
.

Rozwiązując układ równań normalnych
znajdziemy, że:

.

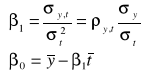
Elementami empirycznej macierzy wariancji-kowariancji błędów estymacji
będą:

,

,

,

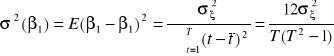
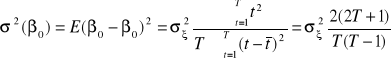
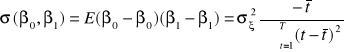
gdzie
jest wariancją reszt z oszacowania modelu.

Większość z przyjętych założeń odnośnie do parametrów rozkładu składników zakłócających może być przedmiotem weryfikacji statystycznej, po oszacowaniu parametrów modelu.

W sprawie zapisu macierzowego modelu zob. np. T.W.Bołt, Wykłady ekonometrii - materiały zamieszczone na stronie internetowej: www.am.gdynia.pl .

Zob. np. T.W.Bołt, Wykłady ekonometrii - materiały zamieszczone na stronie internetowej: www.am.gdynia.pl .

Zobacz Aneks 1.

Wzór ten jest po prostu skalarnym zapisem formy kwadratowej występującej we wzorze na wariancję błędu prognozy ex ante, tj.
.

W sprawie rozkładu błędu ex ante zobacz Aneks 2.

Zobacz Aneks 3.

Zobacz wzór na macierz wariancji i kowariancji błędów estymacji w Aneksie.

Stosując zapis macierzowy otrzymujemy: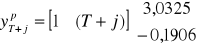
.

W tablicy 1 podana jest wartość średniego błędu reszt równa
. Zatem wariancja reszt ma wartość:
.

Treści zawarte w Aneksach nie są obowiązkowe.

Zob. np. A.S.Goldberger, Teoria ekonometrii, PWE, Warszawa 1975, str. 149.

Zob. A.S.Goldberger, Teoria ekonometrii, PWE, Warszawa 1975, str. 229.

Suma kwadratów reszt jest formą kwadratową wektora składników zakłócających, przy czym
jest idempotentną macierzą o wymiarach
.

Zmienne te są niezależne, gdyż macierze
oraz
są ortogonalne, tj,
.

Prognozowanie i symulacje, Tadeusz W.Bołt, 2003/2004

8

---