Ćwiczenie nr: 88
rok: I	semestr: letni	Pomiar naturalnej aktywności optycznej.
					Ocena:

1. Wiadomości wstępne.

1.1 Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie ze zjawiskiem skręcania płaszczyzny polaryzacji światła w cieczach i kryształach optycznie czynnych oraz wyznaczenie stężenia roztworu cukru na podstawie jego zdolności skręcającej właściwej.

1.2 Wstęp teoretyczny.

W ćwiczeniu używa się sacharymetru przedstawionego schematycznie na rysunku:

Sacharymetr jest rodzajem polaryskopu, a więc przyrządu złożonego z polaryzatora, analizatora oraz umieszczonego między nimi badanego ciała. Nazwa bierze się stąd, że sacharymetr jest polaryzatorem zaopatrzonym w dodatkowe urządzenia, ułatwiające pomiar cukru. Do pomiarów użyto monochromatycznej wiązki światła o długości fali λ. Światło to zostaje spolaryzowane przez półcieniowy polaryzator P, przechodzi przez badany roztwór R albo badaną płytkę kwarcową K, potem przez analizator A, a następnie wpada do oka obserwatora. Półcieniowy polaryzator jest wykonany z dwóch polaryzatorów P₁ i P₂, których płaszczyzny polaryzacji tworzą ze sobą kąt wynoszący około 3˚. Gdyby płaszczyzna analizatora była prostopadła do płaszczyzny polaryzacji części P₁ polaryzatora, wtedy była by wygaszona lewa część pola widzenia. Analogicznie można prawą część pola widzenia. Jeżeli jednak płaszczyzna analizatora jest prostopadła do dwusiecznej kąta między kierunkami przepuszczania obu części P₁ i P₂, to całe pole jest, co prawda przyciemnione, ale jednakowo jasne.

Kąt Γ skręcania płaszczyzny polaryzacji wyznacza się następująco:

Γ= Γ_c∙c∙d

gdzie: c - stężenie roztworu, Γ_c - zdolność skręcająca właściwa, d - droga promienia w ośrodku aktywnym.

Kąt Γ skręcania płaszczyzny polaryzacji można wyznaczyć również z różnicy azymutów. W pustym sacharymetrze ustawiamy analizator na równą jasność obu części pola widzenia i otrzymujemy wówczas azymut α₀, następnie wstawiamy badane ciało i ponownie ustawiamy analizator na równą jasność w ten sposób otrzymujemy azymut α_Z. Gdy mamy oba te azymuty szukany kąt skręcania Γ płaszczyzny polaryzacji wyliczamy ze wzoru:

Γ= α_Z- α₀.

2. Tabele pomiarowe.

• Pomiar stężenia roztworu cukru.

• Wyznaczanie azymutu analizatora dla rurek z roztworami o 0% (woda destylowana), 10% i 15% stężeniem cukru oraz dla rurek X, Y, Z o nieznanym stężeniu:

Lp.	α 0% [˚ ]	α 10% [˚ ]	α 15% [˚ ]	α x [˚ ]	α y [˚ ]	α z [˚ ]
1.	351	6,4	11,0	1,0	6,5	17,5
2.	349	6,5	11,1	0,9	6,7	18,0
3.	351	6,6	11,2	1,0	6,5	18,5
4.	352	7,0	10,8	1,05	6,4	17,0
5.	351	5,5	11,1	0,9	6,5	16,0
6.	351	6,2	10,9	1,05	6,6	16,5
7.	352	6,4	11,0	1,1	6,5	17,5
8.	350	5,9	11,1	1,0	6,4	16,5
9.	351	6,1	10,8	1,05	6,5	17,0
10.	351	6,3	11,0	1,0	6,4	18,0
x	350,9	6,29	11,0	1,0	6,5	17,25
sx	0,28	0,13	0,04	0,02	0,03	0,25

α _0% - azymut dla rurki z wodą destylowaną;

α _10% - azymut dla rurki 10% stężeniu cukru;

α _15% - azymut dla rurki 15% stężeniu cukru;

α _x, α _y, α _z - azymuty dla rurek o nieznany stężeniu.

• Wyznaczanie kąta skręcania płaszczyzny polaryzacji:

Lp.	Γ [˚ ]	ΔΓ [˚ ]	δΓ [%]	Uwagi:
1.	15,39	0,41	2,66	stężenie 10 %
2.	20,1	0,32	1,6	stężenie 15 %
3.	10,1	0,30	2,97	stężenie X %
4.	15,6	0,31	3,00	stężenie Y %
5.	26,35	0,53	2,01	stężenie Z %

1. Obliczanie stężenia roztworów X, Y, Z:

a) roztwór X

Lp.	c [% ]	Δc [% ]	δc [%]	Uwagi:
1.	6,56	0,37	5,64	Γz = 10%
2.	7,54	0,35	4,59	Γz = 15%
	7,05	0,36	5,11	wartość średnia

b) roztwór Y

Lp.	c [% ]	Δc [% ]	δc [%]	Uwagi:
1.	10,14	0,47	4,65	Γz = 10%
2.	11,64	0,42	3,60	Γz = 15%
	10,89	0,44	4,12	wartość średnia

c) roztwór Z

Lp.	c [% ]	Δc [% ]	Δc [%]	Uwagi:
1.	17,12	0,8	4,67	Γz = 10%
2.	19,66	0,7	3,63	Γz = 15%
	18,39	0,75	4,15	wartość średnia

1. Pomiar zdolności skręcania kwarcu.

2.2.1 Wyznaczanie kąta skręcania płaszczyzny polaryzacji:

α₀ = 352˚

Lp.	α [˚ ]	Γ [˚ ]	Uwagi:
1.	330	-22	płytka nr 1 - d1 = -1 mm
2.	310	-42	płytka nr 2 - d2 = -2 mm
3.	24,25	32,25	płytka nr 3 - d3 = 1,5 mm
4.	288	-64	″1+2″ - d = -3 mm
5.	3,5	11,5	″1+3″ - d = 0,5 mm
6.	342,5	-9,5	″2+3″ - d = 0,5 mm
7.	320	-32	″1+2+3″ - d = -1,5 mm

3. Przykładowe obliczenia.

1. Obliczenia dla tabeli 2.1.1:

• średnią wartość obliczamy ze wzoru:

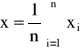
n - liczba pomiarów

x_i - i-ty pomiar

• odchylenie standardowe średniej arytmetycznej liczymy ze wzoru:

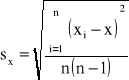
n - liczba pomiarów

x - średnia arytmetyczna

x_i - i-ty pomiar

1. Obliczenia dla tabeli 2.1.2:

• obliczanie kąta skręcania:

α - azymut analizatora z badaną rurką;

α₀ - azymut analizatora z rurką, w której jest woda destylowana;

• błąd kąta skręcania liczymy z różniczki zupełnej:

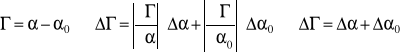
Δα - błąd azymutu analizatora z badaną rurką;

Δα₀ - błąd azymutu analizatora z rurką, w której jest woda destylowana;

2. Obliczenia dla tabeli 2.1.3:

• obliczanie stężenia cukru:

Γ - kąt skręcania badanego roztworu;

Γ_z - kąt skręcania roztworu o znanym stężeniu;

c_z - znane stężenie;

• błąd stężenia wyliczamy z różniczki zupełnej:

;
;
;

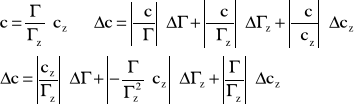
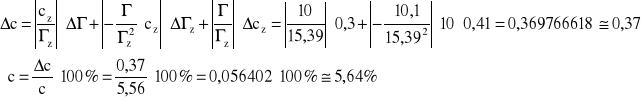
1. Obliczanie dla pomiarów zdolności skręcającej kwarcu:

• sprawdzanie zdolności skręcającej kwarcu przy obrocie analizatora w prawo:

proporcja nie została spełniona;

• sprawdzanie zdolności skręcającej kwarcu przy obrocie analizatora w lewo:

proporcja została spełniona, zatem kwarc jest lewoskrętny.

4. Wnioski.

W pierwszej części ćwiczenia badaliśmy stężenie roztworu cukru. W przeprowadzonym doświadczeniu wykorzystano fakt o jednakowym zaciemnieniu obu połówek pola widzenia, gdy płaszczyzna polaryzacji analizatora jest prostopadła do dwusiecznej kąta półcienia. Po wyznaczeniu kątów skręcania skręceń płaszczyzn dla kolejno badanych próbek i wyznaczeniu stężenia roztworu, z wykresu zależności kąta skręcania Γ od stężenia c cukru w roztworze widać proporcjonalny wzrost kąta wraz ze stężeniem, poza niewielkimi odchyłkami. Świadczy to o niepoprawności wykonania ćwiczenia lub o niewłaściwie dokonanych obliczeniach. W ćwiczeniu istniała konieczność wyznaczenia odchyleń standardowych średniej arytmetycznej (niepewności pomiaru), ponieważ wykonywaliśmy serię pomiarów i uśrednialiśmy wynik. Dodatkowym błędem występującym w ćwiczeniu był niewątpliwie błąd wynikający z niewłaściwego odczytania podziałki sacharymetru, która umożliwiała wyznaczenie kąta z dokładnością 0,01˚. Ponieważ niektóre pomiary nie były wykonywane z dużą dokładnością, więc błąd odczytu wychodził dość duży. Błędy kąta skręcania Γ i stężenia c cukru w roztworze wyznaczyłem posługując się metodą różniczki zupełnej.

W drugiej części ćwiczenia badaliśmy wpływ grubości płytek kwarcowych na kąt skręcania płaszczyzny. Na podstawie pomiarów płytek d₁ i d₂ można stwierdzić, że badany kwarc jest lewoskrętny, ponieważ przy obrocie analizatora w lewo zachodzi proporcja d₁/d₂ = Γ₁/Γ₂, natomiast przy obrocie w prawo proporcja ta nie zostaje spełniona.

---