Państwowa Wyższa Szkoła Zawodowa

im. Prezydenta Stanisława Wojciechowskiego

w Kaliszu

Instytut Politechniczny

Inżynieria Środowiska

Laboratorium z Mechaniki Płynów

Współczynniki oporów przepływu

Przygotowali:

Cel ćwiczenia.

Celem ćwiczenia jest doświadczalne wyznaczenie współczynników oporów przepływu oraz współczynników oporów lokalnych i długości zastępczych dla kilku elementów armatury, w oparciu o pomiary spadków ciśnienia przy przepływie powietrza przez rury. Otrzymane wartości będą porównane z wielkościami literaturowymi.

1. Wprowadzenie.

Podczas przepływu płynów przez przewody i aparaty występują opory przepływu. Powoduje to, że część energii mechanicznej potrzebnej do tłoczenia płynu zamieniana jest na ciepło i ulega rozproszeniu.

Bilans energii mechanicznej przedstawia równanie Bernoulliego:

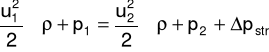
gdzie: u - średnia liniowa prędkość przepływu płynu [m/s], ρ - gęstość płynu [kg/m³], p - ciśnienie statyczne [Pa], Δp_str - straty ciśnienia [Pa].

Wyróżnia się dwa rodzaje strat ciśnienia: Δp_t - straty wynikające z tarcia i ΣΔp_m - straty w wyniku oporów miejscowych (lokalnych).

Opory tarcia spowodowane są lepkością płynu i występują na całej długości przewodu. Wynikają one z tarcia warstw płynu poruszającymi się z różnymi prędkościami. Opory te obrazuje równanie Darcy-Weisbacha:

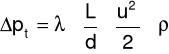
gdzie: L - długość rury [m], d - średnica wewnętrzna rury [m], u - średnia liniowa prędkość przepływu płynu [m/s], ρ - gęstość płynu.

Współczynnik λ nazywa się współczynnikiem oporów przepływu lub współczynnikiem oporów tarcia. Współczynnik ten jest funkcją liczby Reynoldsa i wynosi dla ruchu laminarnego:

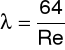
Natomiast dla ruchu burzliwego λ można wyznaczyć z równania Blasiusa dla rur gładkich, obowiązujące dla 3×10³ < Re < 10⁵:

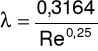
Opory miejscowe związane są z lokalnymi zmianami prędkości i kierunku przepływu wywołanymi przez elementy armatury i inne elementy zainstalowane na rurociągu. Straty ciśnienia spowodowane przez opór miejscowy może być wyrażone równaniem:

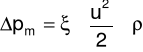
gdzie: ξ jest współczynnikiem oporu miejscowego dla danego rodzaju armatury.

Strata ciśnienia wywołana oporem miejscowym może być także obliczona w oparciu o tzw. Długość zastępczą L_e:

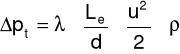
Jak widać z powyższego równania L_e jest długością prostego odcinka rury, w którym strata ciśnienia na skutek oporów tarcia jest taka sama jak strata ciśnienia na skutek oporu miejscowego.

2. Aparatura.

Rys. 1. Schemat aparatury

1 - wentylator, 2 - rura pomiarowa (wymienna), 3 - manometr różnicowy, 4 - przewody impulsowe, 5 - regulator częstości obrotowej silnika wentylatora.

Powietrze z otoczenia zasysane jest za pomocą wentylatora i przepływa przez wymienne rury. W ściankach każdej rury pomiarowej znajdują się dwa otwory do odbioru impulsów ciśnienia połączone z elastycznymi przewodami impulsowymi. Przewody te doprowadzone są do manometru, na którym odczytuje się spadek ciśnienia w hPa podczas przepływu powietrza w odcinku pomiarowym badanej rury.

W zestawie znajdują się oprócz rury prostej jeszcze cztery rury, które w celu wykonania dla nich pomiarów należy instalować kolejno. Są to: rura z zaworem grzybkowym, rura z zaworem kulowym, rura z czterema kolanami i rura ze skokową zmianą średnicy. Pomiary dla każdej z tych rur wykonuje się przy dwóch prędkościach przepływu. Jeden pomiar przy maksymalnej częstości obrotowej silnika wentylatora, a drugi przy takiej, aby ciśnienie różnicowe wyniosło około połowę wartości uzyskanej przy pomiarze poprzednim.

3. Tabela.

Rodzaj badanego elementu	u [m/s]	Δp [Pa]	Re	λlit	λdośw
Rura prosta	4,12	12	10455,1	0,031	0,048
		4,73	15	12003,0	0,030		0,045
		5,56	20	14109,2	0,029		0,044
		6,61	27	16773,8	0,028		0,042
		6,88	30	17458,9	0,028		0,043
		7,04	32	17864,9	0,027		0,044
	u [m/s]	Δp [Pa]	Re	λlit	ξ	Le [m]
Zawór grzybkowy	2,35	68	5963,4	0,036	19,97	22,19
		3,53	164	8957,8	0,033	21,49	26,44
	Zawór kulowy	4,08	20	10353,5	0,031	1,25	1,60
		7,85	59	19920,4	0,027	0,96	1,44
	Kolana	3,27	59	8298,1	0,033	2,33	2,81
		5,47	158	13880,9	0,029	2,23	3,06

temperatura powietrza 22°C gęstość powietrza ρ = 1,18 kg/m³

lepkość powietrza η = 1,86×10^-5 Pa•s d = 0,04 m

długość odcinków pomiarowych rur prostych 1m

długość odcinka pomiarowego rury z kolankami 1,2m

4. Obliczenia.

1. Obliczenia dla rury prostej.

Liczba Reynoldsa:




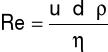
gdzie: u - prędkość przepływu płynu [m/s], d - średnica przewodu [m], ρ - gęstość płynu [kg/m³], η - lepkość płynu [Pa×s]

λ literaturowe:




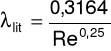
λ doświadczalne:




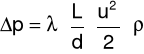
gdzie: Δp - spadek ciśnienia na odcinku pomiarowym [Pa], L - długość odcinka pomiarowego [m], d - średnica wewnętrzna rury [m], u - prędkość przepływu powietrza w rurze [m/s], ρ - gęstość powietrza [kg/m³]

Po przekształceniu otrzymujemy:




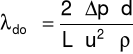
d = 0,04m, ρ = 1,18 kg/m³, η = 1,86×10^-5 Pa×s,

1. dla prędkości przepływu u = 4,12m/s oraz spadku ciśnienia Δp = 12Pa










2. dla prędkości przepływu u = 4,73m/s oraz spadku ciśnienia Δp = 15Pa










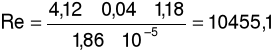
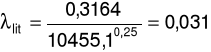
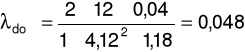
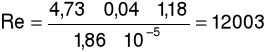
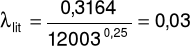
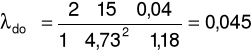
c) dla prędkości przepływu u = 5,56m/s oraz spadku ciśnienia Δp = 20Pa










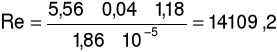
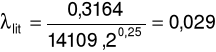
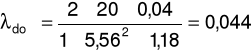
d) dla prędkości przepływu u = 6,61m/s oraz spadku ciśnienia ၄p = 27Pa










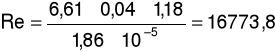
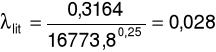
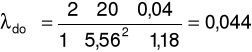
e) dla prędkości przepływu u = 6,88m/s oraz spadku ciśnienia ၄p = 30Pa










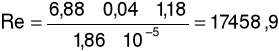
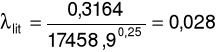
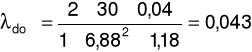
f) dla prędkości przepływu u = 5,56m/s oraz spadku ciśnienia ၄p = 32Pa










2. Obliczenia dla zaworu grzybkowego.

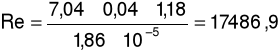
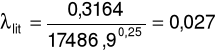
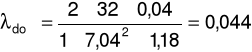
Liczba Reynoldsa:




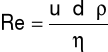
gdzie: u - prędkość przepływu płynu [m/s], d - średnica przewodu [m], ρ - gęstość płynu [kg/m³], η - lepkość płynu [Pa×s]

λ literaturowe:




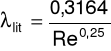
Współczynnik oporów lokalnych ξ:




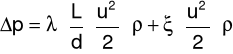
gdzie: Δp - spadek ciśnienia na odcinku pomiarowym [Pa], L - długość odcinka pomiarowego [m], d - średnica wewnętrzna rury [m], u - prędkość przepływu powietrza w rurze [m/s], ρ - gęstość powietrza [kg/m³], ξ - współczynnik oporów lokalnych.

Po przekształceniu otrzymujemy:




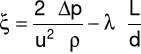
Długość zastępcza:




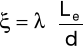
Po przekształceniu otrzymujemy:


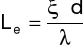
[m]

a) dla prędkości przepływu u = 2,35m/s oraz spadku ciśnienia ၄p = 68Pa











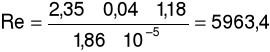
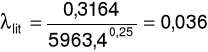
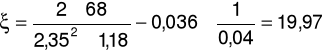
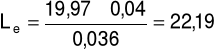
m

b) dla prędkości przepływu u = 3,53m/s oraz spadku ciśnienia ၄p = 164Pa











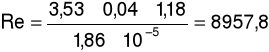
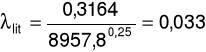
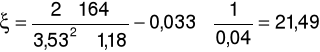
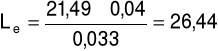
m

3. Obliczenia dla zaworu kulowego.

Wzory takie jak w przypadku zaworu grzybkowego.

a) dla prędkości przepływu u = 4,08m/s oraz spadku ciśnienia ၄p = 20Pa













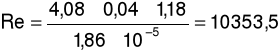
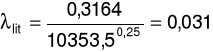
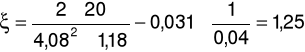
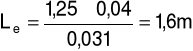
b) dla prędkości przepływu u = 7,85m/s oraz spadku ciśnienia ၄p = 59Pa













4. Obliczenia dla kolan.

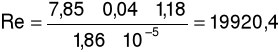
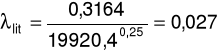
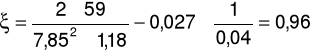
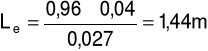
Liczba Reynoldsa:




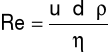
λ literaturowe:




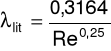
Współczynnik oporów lokalnych ξ:




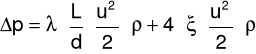
Po przekształceniu otrzymujemy:




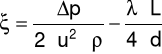
Długość zastępcza:




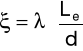
Po przekształceniu otrzymujemy:


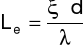
[m]

a) dla prędkości przepływu u = 3,27m/s oraz spadku ciśnienia ၄p = 59Pa













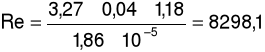
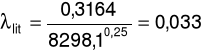
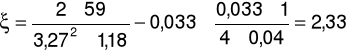
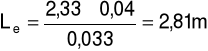
b) dla prędkości przepływu u = 5,47m/s oraz spadku ciśnienia ၄p = 158Pa













5. Wnioski.

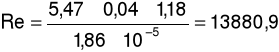
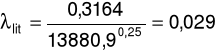
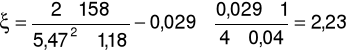
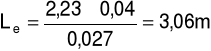
Na podstawie dokonanych pomiarów oraz dokonanych obliczeń otrzymaliśmy wartości współczynnik oporów przepływu, współczynnik oporów lokalnych oraz długości zastępcze dla poszczególnych elementów armatury. Wartości współczynników λ_lit oraz λ_dośw różnią się między sobą.

Współczynniki oporów przepływu oraz współczynniki oporów lokalnych mają różne wartości dla poszczególnych elementów armatury.

2

---