Politechnika Wrocławska Wrocław, 07,05,2001

Wydział Górniczy

Wytrzymałość skał w trójosiowym stanie naprężeń

Kryterium Coulomba - Mohra

Kryterium Hoeka - Browna

Prowadzący: Wykonali:

Dr inż. A. Wojtaszek Krzysztof Hozer Piotr Rogal

Wstęp

Złożoność warunków i stanów obciążeń skał zalegających w masywie wymaga badania ich własności mechanicznych w trójosiowym stanie naprężeń. Przeprowadzenie takich badań jest możliwe w laboratorium, przy zastosowaniu specjalnych urządzeń ciśnieniowych pozwalających na modelowanie stanu naprężeń zbliżonych do naprężeń naturalnych.

Zróżnicowanie składowych stanu naprężenia osiąga się poddając próbkę skalną działaniu wszechstronnego ciśnienia. Stosuje się więc zasadę Karmana, według której na jednoosiowy stan naprężenia nakłada się hydrostatyczny stan ciśnień ( σ₁>σ₂=σ₃ ). Badania przeprowadza się na próbkach walcowych, dla których większe naprężenie główne σ₁ jest przykładane zgodnie z osią pionową próbki, natomiast mniejsze naprężenie główne σ₂ = σ₃ oddziaływuje po obwodzie próbki w kierunku radialnym. Badanie przeprowadza się w komorze Karmana (rys.1), w której realizowany jest osiowo-symetryczny stan naprężenia. Ciśnienie boczne jest wywierane przez olej, natomiast obciążenie pionowe można uzyskać w sposób mechaniczny (prasa hydrauliczna).

Odpowiednio spreparowaną próbkę umieszcza się w specjalnej osłonie gumowej, która nie pozwala na penetrację oleju w pory próbki. Całość umieszcza się w komorze. Próbka ma średnicę 40 mm i smukłość równą 1.

W celu odwzorowania stanu naprężeń, jaki panuje w górotworze, stosuje się ciśnienia w zakresie do 100 MN/m² dla ciśnienia bocznego i do 400 MN/m² dla ciśnienia pionowego. Stosowanie tak dużych ciśnień bocznych wywieranych przez olej na próbkę wymaga opracowania specjalnych rodzajów uszczelnień w systemie hydraulicznym oraz w komorze badawczej.

Typowe badanie skał w aparacie trójosiowego ściskania polega na określeniu wytrzymałości pięciu próbek pochodzących z tej samej próbki pierwotnej, przy różnych ciśnieniach bocznych. No ogół przyjmuje się następujące stopnie ciśnienia bocznego: 20, 40, 60, 80, 100 MN/m².

Zniszczenie próbek poddanych wszechstronnemu ciśnieniu następuje powoli, przy jednoczesnym wzroście ciśnienia w układzie hydraulicznym i spadku obciążenia pionowego. W warunkach jednoosiowego ściskania próbki rozpadają się zazwyczaj na drobne odłamki, a w niektórych przypadkach występują dwa stożki okruchowe. Natomiast w stanie trójosiowego ściskania zniszczenie próbek jednorodnych następuje wzdłuż powierzchni zorientowanych ukośnie do podstawy. Charakterystyczne jest pojawienie się na powierzchniach bocznych poziomych pęknięć, równoległych do podstaw.

Opracowanie wyników przy użyciu kryterium Coulomba-Mohra polega na wykreśleniu obwiedni granicznych kół naprężeń (Mohra) reprezentujących ciśnienia wywierane na próbki w poszczególnych etapach badania, przy zadanym ciśnieniu bocznym. W tym celu nanosi się w układzie współrzędnych σ-τ poszczególne wartości i wykreśla się styczną, która jest w najprostrzym przypadku linią prostą opisaną równaniem Coulomba:

τ = σ tanϕ + c τ-naprężenie ścinające (styczne), [MPa]

σ -naprężenie normalne, [MPa]

ϕ -kąt tarcia wewnętrznego, [°]

c -kohezja (spójność), [MPa].

Następnie wprowaedzając dane do komputera, przy użyciu arkusza kalkulacyjnego Excel, określiliśmy metodą najmniejszych kwadratów równanie prostej y = ax + b, które odpowiada równaniu: . Z powyższego równania wyliczamy kąt tarcia wewnętrznego ϕ. Natomiast spójność c obliczamy na podstawie wzoru: .

Przy opracowaniu wyników według kryterium Hoeka - Browna naprężenia główne określa się wzorem: , gdzie parametrami są R_c i m_i. Przekształcając powyższe równanie otrzymujemy: , które odpowiada równaniu prostej: y = ax + b.

Kryterium Coulomba - Mohra

1.Skała słaba -sól kamienna czysta biała gróbokrystaliczna.

R_r = 1,3, ;1,5 ;1,2 ;1,4 [MPa],

R_c = 28,5 ;25,2 ;31,1 ;29,0 ;24,0 ;27,0 ;29,2 ;26,6 [MPa],

σ3 [MPa]	σ1 [MPa]
5	52,2
10	74,5
15	96,0

Parametry jednoosiowego stanu naprężeń:

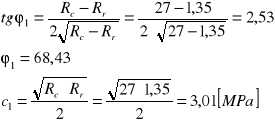
Po aproksymacji prostej w układzie σ₁-σ₃ otrzymujemy równanie postaci y = ax + b, gdzie a = 4,6125 i b = 27,72 , a tym samym y = 4,6125x + 27,72.

Równanie to odpowiada równaniu:

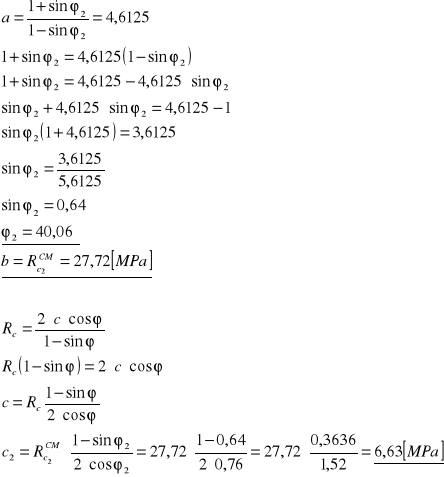
Zestawienie wyników w tabeli:

σ3 [MPa]	σ1 [MPa]	ϕ1 [°]	c1 [MPa]	ϕ2 [°]	c2 [MPa]	Rc2^CM [MPa]
5	52,2	68,43	3,01	40,06	6,63	27,72
10	74,5
15	96,0

1.Skała mocna - zlepieniec drobnoziarnisty

R_r = 3,6 ; 3,4 ; 3,2 [MPa],

R_c = 48,1 ; 66,6 ; 23,7 ; 72,4 ; 69,7 ; 51,1 [MPa],

σ3 [MPa]	σ1 [MPa]
20	147,3
40	181,2
60	220

Parametry jednoosiowego stanu naprężeń:

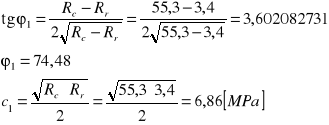
Po aproksymacji prostej w układzie σ₁-σ₃ otrzymujemy równanie postaci y = ax + b, gdzie a = 2,9148 i b = 58,924 , a tym samym y = 2,9148x + 58,924.

Równanie to odpowiada równaniu:

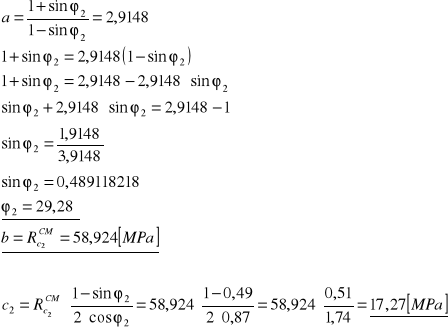
Zestawienie wyników w tabeli:

σ3 [MPa]	σ1 [MPa]	ϕ1 [°]	c1 [MPa]	ϕ2 [°]	c2 [MPa]	Rc2^CM [MPa]
20	147,3	74,48	6,86	29,28	17,27	58,924
40	181,2
60	220

Kryterium Hoeka - Browna

1.Skała słaba -. sól kamienna czysta biała gróbokrystaliczna

R_r =1,3, ;1,5 ;1,2 ;1,4 [MPa],

R_c = 28,5 ;25,2 ;31,1 ;29,0 ;24,0 ;27,0 ;29,2 ;26,6 [MPa],

σ3 [MPa]	σ1 [MPa]
0	28,5	812,25
0	25,2	635,04
0	31,1	967,21
0	29,0	841
0	24,0	576
0	27,0	729
0	29,2	852,64
0	26,6	707,56
5	52,2	2227,84
10	74,5	4160,25
15	96,0	6561

Po wprowadzeniu danych do arkusza kalkulacyjnego Excel określiliśmy metodą najmniejszych kwadratów równanie prostej y = ax + b, które odpowiada równaniu . Współczynnikiem kierunkowym prostej jest .

Równanie prostej:

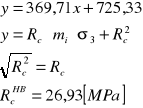
Określenie parametru m_i:

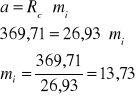
1.Skała mocna - zlepieniec drobnoziarnisty.

.

R_r = 3,6 ; 3,4 ; 3,2 [MPa],

R_c = 48,1 ; 66,6 ; 23,7 ; 72,4 ; 69,7 ; 51,1 [MPa],

σ3 [MPa]	σ1 [MPa]
0	48,1	2313,61
0	66,6	4435,56
0	23,7	561,69
0	72,4	5241,76
0	69,7	4858,09
0	51,1	2611,21
20	147,3	16205,29
40	181,2	19937,44
60	220	25600

Po wprowadzeniu danych do arkusza kalkulacyjnego Excel określiliśmy metodą najmniejszych kwadratów równanie prostej y = ax + b, które odpowiada równaniu . Współczynnikiem kierunkowym prostej jest .

Równanie prostej:

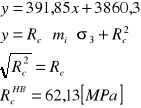
Określenie parametru m_i:

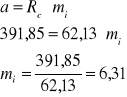
Przykładowe wyniki badań mechanicznych własności skał w trójosiowym stanie naprężeń:

Rodzaj skały	Naprężenie poziome	Naprężenie pionowe	Wytrzymałość na ściskanie	Kohezja i	kąt tarcia c,	wewnętrz ϕ	nego
	σ2 σ3	σ1	Rc	w jednoos nie napręż	iowym sta enia	w trójosio nie napręż	wym sta enia
	[MPa]	[MPa]	[MPa]	c1 [MPa]	ϕ1 [°]	c2 [MPa]	ϕ2 [°]
Piaskowiec szary, masywny, silnie zwięzły	0 20 40 60	201,8 326,3 448,5 563,8	201,8	32	67	50	43
Dolomit ciemnoszary, ilasty, masywny, silnie zwięzły	0 20 40 60	265,5 455,3 584,4 751,3	265,5	36	72	60	49
Anhydryt jasnoszary, masywny	0 20 40 60	127,3 228,5 283,4 342,3	127,3	22	64,5	40	30
Wapień szary, zwięzły, pelityczny	0 20 40 60	115,3 205,6 259,0 312,8	115,3	19	65,5	46	27
Wapień szary, ilasty	0 20 40 60	62,3 96,4 126,6 156,4	62,3	8,5	60	11	28
Piaskowiec brunatno - czerwony, kruchy	0 20 40 60	26,8 67,0 90,4 117,5	26,8	4,5	58	14	24
Iłowiec szaroseledynowy, zaburzony	0 20 40 60	24,2 62,2 93,6 119,2	24,2	4	57	15	24,5

---