POLITECHNIKA ŁÓDZKA

FILIA W BIELSKU - BIAŁEJ

wydz. F.T.I. i M.S.

kierunek: INFORMATYKA

semestr: II

grupa nr 208

ĆWICZENIE NR 15

WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W POWIETRZU I CIAŁACH STAŁYCH.

Wykonali :

Bartosz Korczyk

Krzysztof Ślemp

Grzegorz Frej

I. Wprowadzenie teoretyczne i opis stanowiska doświadczalnego :

Falą nazywamy lokalne zaburzenie pojawiające się w ośrodku sprężystym, przenoszone dzięki oddziaływaniom międzycząsteczkowym w coraz dalsze obszary ośrodka. Gdy zaburzenie ma charakter sinusoidalny cząstki wykonują drgania harmoniczne.

Jeżeli drgania zachodzą w kierunku rozchodzenia się fali, to nazywamy ją wtedy falą podłużną, jeżeli w kierunku prostopadłym - falą poprzeczną. O fali płaskiej mówimy wtedy, gdy punkty drgające w jednakowej fazie tworzą układ płaszczyzn równoległych.

Iloczyn V⋅T=λ określa drogę, jaką przebywa fala w czasie równym okresowi drgań (długości fali).

Fale pochodzące z różnych źródeł mogą się rozprzestrzeniać w tym samym ośrodku. Wówczas punkty tego ośrodka wykonują drgania złożone, będące sumą drgań pochodzących z różnych źródeł. Źródła drgające z tą samą częstością i stałą w czasie różnicą faz oraz pochodzące od nich fale nazywamy spójnymi.

Częstym przypadkiem interferencji są fale stojące. Fala stojąca powstaje w wyniku interferencji dwóch fal harmonicznych o jednakowych częstościach, amplitudach i kierunkach drgań. Punkty, w których amplituda wynosi zero, które w przestrzeni spełniają warunek:

n=0,1,2...

nazywamy węzłami fali. Położenie tych punktów nie zmienia się w czasie i dlatego fala ta nosi nazwę stojącej.

Punkty spełniające warunek:

nazywamy strzałkami fali stojącej. W punktach tych amplituda osiąga wartość maksymalną. Odległość między sąsiednimi strzałkami wynosi λ/2, natomiast między sąsiednimi strzałką i węzłem - λ/4.

Do pomiaru prędkości dźwięku w różnych ośrodkach wykorzystaliśmy metodę rezonansu. Rezonans ma miejsce wtedy, gdy częstotliwość drgań źródła wzbudzającego drgania pokrywa się z jedną z częstotliwości drgań własnych wzbudzanego układu.

1. Wyznaczanie prędkości fali dźwiękowej w powietrzu.

Do doświadczenia został użyty przyrząd, będący naczyniem połączonym, którego jedno ramię stanowi butelka z wodą, drugie - rura szklana z podziałką, umożliwiającą odczytanie zmiany położenia poziomu wody.

Wykorzystaliśmy tutaj zjawisko rezonansu akustycznego pomiędzy drgającym kamertonem a drganiami słupa powietrza nad wodą w rurze. Zmieniając poziom wody możemy tak dobrać wysokość słupa powietrza, aby spełniony był warunek rezonansowy:

gdzie:

l - długość rury,

λ - długość fali.

Spełnienie go powoduje wyraźne wzmocnienie dźwięku. Fala stojąca w słupie powietrza będzie miała wówczas węzeł przy powierzchni wody i strzałkę u wylotu rury. Zmierzyliśmy odległość h pomiędzy położeniami (dwoma) poziomu cieczy, dla których słychać w słuchawce wzmocnienie dźwięku Jeśli są to wzmocnienia następujące kolejno po sobie, to wówczas:

stąd: λ = 2⋅(h₂-h₁)

Prędkość fali wyznaczamy ze wzoru:

V=2⋅f_k

gdzie:

f_k - jest częstością drgań własnych kamertonu.

2. Wyznaczanie prędkości fali dźwiękowej w metalu

Do wyznaczania prędkości fali w prętach wykorzystaliśmy rurę Kundta. Jak wiemy fale biegnące w obydwu kierunkach w pręcie (metalowym lub szklanym) odbijają się bez zmiany fazy od końców pręta i w wyniku interferencji tworzą falę stojącą.

Pręt będzie drgał w fazie ze źródłem, jeśli:

Rezonans pomiędzy drganiami podłużnymi w pręcie wykonanym z badanego materiału i drganiami słupa powietrza w szklanej rurze ograniczonego płytką na końcu badanego pręta i zakończeniem przysłony został wykorzystany w doświadczeniu Kundta. Pręt zamocowany jest dokładnie w środku swojej długości:

W pręcie powstaje fala stojąca z węzłem w środku i strzałkami na końcach. Drgający pręt jest źródłem fali dźwiękowej, która rozchodzi się także i w słupie powietrza w rurze. Jeżeli długość tego słupa spełnia warunek rezonansowy, to tworzy się fala stojąca. Po dokonaniu odpowiednich pomiarów możemy obliczyć prędkość dźwięku w materiale:

gdzie:

n - ilość połówek fali stojącej,

l - długość pręta,

L - długość słupa powietrza.

Jeżeli oznaczymy odpowiednio λ₁ i V₁, λ i V - długość i prędkość fali w pręcie i powietrzu, to dla rezonansu zachodzi:

Długość fali w powietrzu i pręcie wyznaczamy z zależności:

λ₁=2⋅l

Prędkość fali dźwiękowej (V₁) zależy od gęstości badanego materiału i modułu Younga:

gdzie:

E - moduł Younga,

ρ - gęstość.

W celu uwiarygodnienia wyników, obliczamy także maksymalne błędy bezwzględne:

II. Wyniki pomiarów i obliczeń.

1. Obliczenia do doświadczenia Quinckiego:

h₁ = 0,22 m

h₂ = 0,61 m

h = h₂ - h₁ = 0,61 - 0,22 = 0,39 m

⇒ λ=2⋅h

λ = 2 ⋅ 0,39 = 0,78 m

f_k = 435 Hz

V = λ⋅f_k = 0,78 ⋅ 435 = 339 m/s

Δh = Δh₁ = Δh₂ ⇒ Δh = ± 0,01 m

ΔV
± 17 m/s

Tabela nr1.

h1	h2	fk	h	V	ΔV
m	m	Hz	m	m/s	m/s
0,22	0,61	435	0,39	339	17

2. Obliczenia do doświadczenia Kundta:

a) pręt aluminiowy:

l = 0,93 m

L =1 m

λ₁ = 2 ⋅ l = 2 ⋅ 0,93 = 1,86 m

n = 15

dla rezonansu:

m/s

V₁=4855 m/s

Δl = ± 0,001 m

ΔL = ± 0,005 m

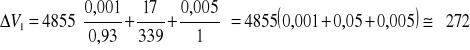
m/s

Moduł Younga dla aluminium obliczamy ze wzoru:

gdzie:

ρ - gęstość aluminium ( ρ = 2,7 g/cm³ )

2,7 g/cm³ = 2700 kg/m³

E = V₁²⋅ρ = 4855² ⋅ 2700 = 6,4 ⋅ 10¹⁰ N/m²

N/m²

b) pręt miedziany:

l = 0,92 m

L = 1 m

λ₁ = 2 ⋅ l = 2 ⋅ 0,92 = 1,84 m

n = 13

dla rezonansu:

m/s

V₁=4162 m/s

Δl = ± 0,001 m

ΔL = ± 0,005 m

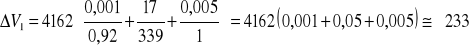
m/s

Moduł Younga dla miedzi obliczamy ze wzoru:

gdzie:

ρ - gęstość miedzi ( ρ = 8,93 g/cm³ )

8,93 g/cm³ = 8930 kg/m³

E = V₁²⋅ρ = 4162² ⋅ 8930 = 1,5 ⋅ 10¹¹ N/m²

N/m²

Tabela nr2.

Rodzaj Pręta	l	Δl	L	ΔL	n	V1	ΔV1	E	ΔE
		m	m	m	m		m/s	m/s	N/m^2	N/m^2
Aluminium	0,93	0,001	1	0,005	15	4855	272	6,4 ⋅10^10	0,7⋅10^10
Miedź	0,92	0,001	1	0,005	13	4162	233	1,5⋅10^11	0,2⋅10^11

III. Wyniki końcowe.

1. Prędkość d*więku w powietrzu:

V = V_obl. ± ΔV = 339 ± 17

2. Prędkość d*więku w ciałach stałych:

a) dla Al V₁ = V_obl ± ΔV₁ = 4855 ± 272

b) dla Cu. V₁ = V_obl ± ΔV₁ = 4162 ± 233

3. Moduł Younga :

a) dla Al E = E ± ΔE = 6,4⋅10¹⁰ ± 0,7⋅10¹⁰

b) dla Cu E= E ± ΔE1 = 1,5⋅10¹¹ ± 0,2⋅10¹¹

7

---