SPRAWOZDANIE z ćw. nr 20 Temat:: Skalowanie termopary i wyznaczanie temperatury krzepnięcia stopu.
|
LABORATORIUM z FIZYKI OGÓLNEJ PRACOWNIA I INSTYTUT FIZYKI POLITECHNIKI WROCŁAWSKIEJ |
||
Magdalena Śmieszniak Wydział M.-E Rok II |
Data wykonania ćw.
16.11.1998 r. |
Ocena:
|
|
1. CEL ĆWICZENIA
Celem ćwiczenia jest poznanie fizycznych podstaw zjawiska termoelektrycznego i zapoznanie z techniką pomiaru temperatury za pomocą termopary.
2. WSTĘP TEORETYCZNY
Zjawisko termoelektryczne polega na powstaniu siły elektromotorycznej między spojeniami dwóch różnych metali, jeżeli między tymi spojeniami występuje różnica temperatur. Zjawisko to wykorzystuje się do pomiaru temperatury. Zastosowanie termopar umożliwia zdalny pomiar temperatury, rejestrację zmian temperatury, automatyczną regulację procesów technologicznych oraz pomiar temperatury bardzo małych obiektów. Dodatkowymi zaletami termopar są: ich prosta konstrukcja, trwałość, bardzo duży zakres pomiarowy, dokładność i czułość pomiaru oraz mała bezwładność cieplna.
Metal jest zbudowany z jonów dodatnich tworzących sieć krystaliczną oraz elektronów swobodnych poruszających się między tymi jonami. Koncentracja elektronów swobodnych jest różna w różnych metalach, a ponadto zależy od temperatury. W miejscu styku następuje dyfuzja elektronów z metalu o większej koncentracji elektronów swobodnych do metalu o mniejszej koncentracji.
W obwodzie zamkniętym złożonym z dwóch różnych metali, gdy temperatury styków są jednakowe, następuje kompensacja napięcia Uab, powstałego na jednym ze styków, przez napięcie Uba na drugim styku. W obwodzie prąd nie płynie.
Jeżeli temperatury styków będą się różnić między sobą T1≠T2 , to napięcie kontaktowe Uab ≠Uba i w obwodzie popłynie prąd termoelektryczny. Na gruncie elektronowej teorii metali w złączu wykonanym z dwóch metali A i B ,to powstanie kontaktowa różnica potencjałów
,gdzie:
e - ładunek elektronu,
- energia Fermiego dla metalu A
- energia Fermiego dla metalu B.
W praktyce, dla niedużych różnic temperatur między spoinami można przyjąć liniową zależność siły termoelektrycznej od różnicy temperatur.
Stała α nazywa się współczynnikiem termoelektrycznym i oznacza wartość siły termoelektrycznej dla termopary wykonanej z danej pary metali przy różnicy temperatur między spojeniami równej 1 K.
3. SCHEMAT POMIAROWY
Schemat pomiaru temperatury za pomocą termopary
Przed przystąpieniem do pomiaru temperatury przeprowadziliśmy skalowanie termopary. Polega ono na doświadczalnym wyznaczeniu zależności siły termoelektrycznej od temperatury. W tym celu umieszcza się jedno ze spojeń termopary w mieszaninie wody z lodem a drugie w pojemniku, w którym możemy zmieniać temperaturę w sposób kontrolowany. W podgrzewanym naczyniu znajdowała się termopara i termometr.
4. POMIARY I OBLICZENIA
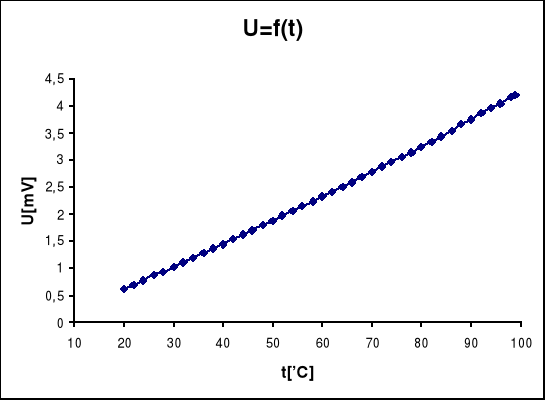
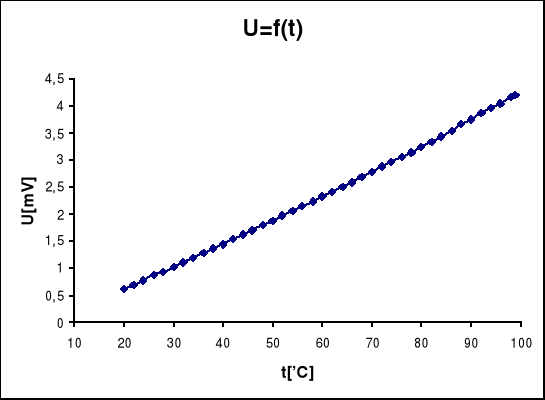
Pomiary przeprowadzone w celu wyskalowania termopery:
t[°C] |
U[V] |
t[°C] |
U[V] |
t[°C] |
U[V] |
t[°C] |
U[V] |
20 |
0,607 |
42 |
1,531 |
62 |
2,413 |
82 |
3,343 |
22 |
0,692 |
44 |
1,619 |
64 |
2,508 |
84 |
3,440 |
24 |
0,771 |
46 |
1,706 |
66 |
2,595 |
86 |
3,533 |
26 |
0,859 |
48 |
1,790 |
68 |
2,689 |
88 |
3,666 |
28 |
0,937 |
50 |
1,880 |
70 |
2,779 |
90 |
3,756 |
30 |
1,024 |
52 |
1,971 |
72 |
2,874 |
92 |
3,865 |
32 |
1,102 |
54 |
2,058 |
74 |
2,969 |
94 |
3,958 |
34 |
1,188 |
56 |
2,144 |
76 |
3,054 |
96 |
4,054 |
36 |
1,275 |
58 |
2,236 |
78 |
3,148 |
98 |
4,158 |
38 |
1,360 |
60 |
2,327 |
80 |
3,243 |
99 |
4,205 |
40 |
1,444 |
--- |
--- |
--- |
--- |
--- |
--- |
Wzory i obliczenia.
Podczas ćwiczenia posłużono się wzorem, w którym temperatura wyrażona jest w stopniach Celsjusza. Przy temperaturze odniesienia równej 0 równanie na siłę termoelektryczną wyraźnie się upraszcza do postaci :
stąd dla n pomiarów otrzymujemy :
Badanie zjawiska krzepnięcia metalu.
Opis układu pomiarowego.
Zastosowano ten sam zestaw, co w poprzednim punkcie z tą różnicą, że probówkę z termoparą umieszczono w metalowym naczyniu z łatwo topliwym metalem.
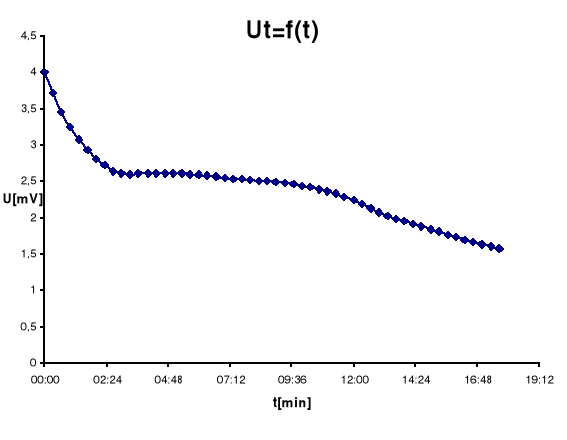
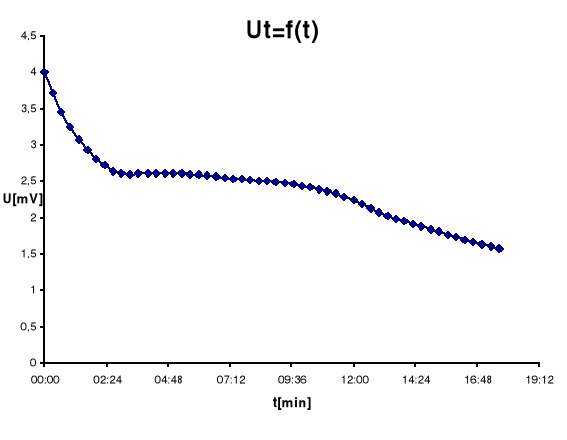
Wyznaczanie temperatury krzepnięcia metalu.
Tabele pomiarów:
t[min] |
U[mV] |
t[min] |
U[mV] |
00:00 |
4 |
09:00 |
2,491 |
00:20 |
3,707 |
09:20 |
2,477 |
00:40 |
3,449 |
09:40 |
2,459 |
01:00 |
3,252 |
10:00 |
2,439 |
01:20 |
3,073 |
10:20 |
2,415 |
01:40 |
2,923 |
10:40 |
2,388 |
02:00 |
2,809 |
11:00 |
2,359 |
02:20 |
2,721 |
11:20 |
2,327 |
02:40 |
2,641 |
11:40 |
2,29 |
03:00 |
2,604 |
12:00 |
2,241 |
03:20 |
2,594 |
12:20 |
2,18 |
03:40 |
2,605 |
12:40 |
2,127 |
04:00 |
2,611 |
13:00 |
2,074 |
04:20 |
2,612 |
13:20 |
2,027 |
04:40 |
2,612 |
13:40 |
1,985 |
05:00 |
2,61 |
14:00 |
1,946 |
05:20 |
2,606 |
14:20 |
1,907 |
05:40 |
2,599 |
14:40 |
1,875 |
06:00 |
2,589 |
15:00 |
1,84 |
06:20 |
2,579 |
15:20 |
1,804 |
06:40 |
2,566 |
15:40 |
1,768 |
07:00 |
2,55 |
16:00 |
1,73 |
07:20 |
2,539 |
16:20 |
1,693 |
07:40 |
2,528 |
16:40 |
1,659 |
08:00 |
2,519 |
17:00 |
1,625 |
08:20 |
2,511 |
17:20 |
1,596 |
08:40 |
2,502 |
17:40 |
1,566 |
Wzory i obliczenia.
Przy wyznaczaniu temperatury krzepnięcia skorzystano z wyznaczonego w poprzednim punkcie współczynnika termoelektrycznego. Przy zaokrąglaniu wzięto pod uwagę błędy pomiarowe : błąd kwantyfikacji woltomierza i błąd bezwzględny termometru, odpowiednio : ΔU = 0,001 V i Δt = 0,5 °C.
Metoda --> [Author:ZF] --> [Author:ZF] regresji liniowej:
, gdzie
Otrzymaliśmy następujące wyniki:
M=938120
a=0.045444357862
-b=0.36530917044
y = ax+b
Prosta musi przechodzić przez punkty :
Z otrzymanych wyników można wyliczyć temperaturę ze związku:
Odchylenie standardowe
Dla temperatur bląd względny wynosi odpowiednio:
Dla woltomierza bląd względny wynosi odpowiednio:
5. WNIOSKI I DYSKUSJA BŁĘDÓW POMIAROWYCH
Pomiary prowadzone podczas ćwiczenia obarczone były szeregiem błędów. Po pierwsze występowały błędy wynikające z zastosowanych przyrządów : ΔU = 0,001 V i Δt = 0,5 °C. Łatwo można dostrzec większą rolę błędu bezwzględnego termometru. Po przejściu na błędy względne sytuacja wygląda jeszcze gorzej. Tak więc widzimy, że błędy woltomierza przy błędach termometru są do zaniedbania. Obserwując charakter błędu względnego dostrzegamy, że przyjmuje on największą wielkość przy początku skali. Dysponując wykresami zależności napięcia termoelektrycznego od czasu, zauważono charakter zjawiska krzepnięcia dla badanego metalu. Po zapoczątkowaniu procesu krystalizacji metal zaczął oddawać ciepło do otoczenia, temperatura wyraźnie wzrosła. Krzywa zależności T=f(t) (temperatury od czasu) po osiągnięciu minimum lokalnego trochę wzrasła i później zaczęła maleć. To minimum to temperatura krzepnięcia dla badanego metalu. Uzyskany poziom temperatury (66°C) wskazuje, że mieliśmy do czynienia z metalem łatwo topliwym. Dla pewności uzyskanych wynoków obliczenia wykonano korzystając z rygresji liniowej i stwierdzono równoznaczne wyniki z otrzymanymi.
W wykresie U = f(t), przy kwantyfikacji pomiaru co 20 sekund widzimy, że liczba i częstość wykonanych pomiarów mają wpływ na jakość wykresu.Widać, że krzywe oddają charakter zjawiska.
Wyszukiwarka
Podobne podstrony:
33 'napięcie powierzchniowe, Pliki Studia
Tabelka Geometria Wykreślna, Pliki, Studia PK (Mechaniczny & WIL), Geometria wykreślna
FIZYKA78, Pliki Studia
Zmienna losowa i rozklad prawdopodobienstwa - zadania, Pliki, Studia PK (Mechaniczny & WIL)
SPRAWOZDANIE 1, Pliki Studia
cywilizacja żydowska, PLIKI, Studia, WSB, Stosunki Międzynarodowe, 6 semestr, Cywilizacja w czasie i
Lab16 (1), Pliki, Studia PK (Mechaniczny & WIL), Fizyka, Laboratoria, Lab 16
Ocena działań na rzecz ochrony środowiska w mieście Łomża, pliki studia, materiały i prace studia
eko odp mini, Pliki, Studia PK (Mechaniczny & WIL), Ekologia
24 , Pliki Studia
materialoznawstwo, Pliki Studia
więcej podobnych podstron