Teoria Maszyn i Mechanizmów

Analiza Mechanizmu:

1. Synteza strukturalna i geometryczna mechanizmu

1. 
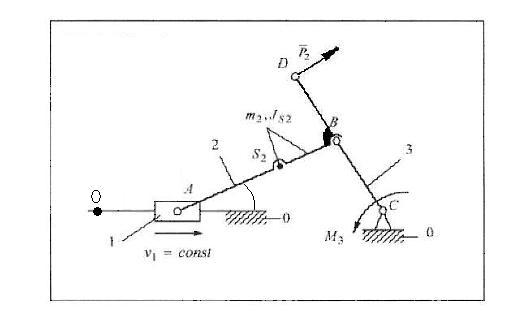
   Na postawie symbolicznego zapisu struktury i parametrów łańcucha kinematycznego budujemy jego schemat ideowy:

Dodatkowo przyjmuję wymiary mojego mechanizmu:

|AB|=1[m]

|BC|=0,7[m]

|OC|=1,9559 [m]

|BD|=0,4 [m]

dodatkowo dla danego położenia początkowego przyjmuję następujące dane:

|0A|=0,6[m]

φ₂=30°

Człon napędzający posiada następującą prędkość i przyspieszenie

2. Ruchliwość i klasy mechanizmu:

a)ruchliwość

w- ruchliwość mechanizmu

n- liczba członów mechanizmu

i- klasa par występujących w łańcuchu kinematycznym

p₄- para kinematyczna klasy czwartej

p₅- para kinematyczna klasy piątej

Wyznaczenie ruchliwości analizowanego mechanizmu

n= 3

p₄=0

p₅=4

Ruchliwość mechanizmu w=1

b)klasy mechanizmu:

Po odłączeniu członu napędzającego 1 pozostałe człony 2 i 3 tworzą grupę strukturalną.

Grupa strukturalna analizowanego mechanizmu jest klasy II

2. Analiza kinematyczna mechanizmu.

1. Analiza kinematyczna mechanizmu metoda grafoanalityczna.

Analiza kinematyczna wykonana jest dla jednego wybranego położenia mechanizmu.

1. Grafoanalityczna analiza prędkości mechanizmu.

Wyznaczanie prędkości V_A .

Zgodnie z przyjętą prędkością członu napędzającego, prędkość V_A=1

Wyznaczanie prędkości V_B

W tym celu skorzystam własności dodawania trójkątów. Jak widać na rysunku, wektor prędkości
jest równoległy do odcinka |OA|, wektor prędkości
jest prostopadły do odcinka |BC|, oraz wektor prędkości
jest prostopadły do odcinka |AB|. Możemy więc zapisać równanie opisujące daną zależność na podstawie rysunku.

Wyznaczanie prędkości punktu V_D

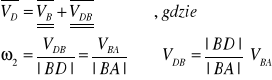
Wektor prędkości
jest prostopadły |DB|

Wyznaczanie prędkości środka masy

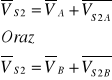
Przyjęcie podziałki rysunkowej dla planu prędkości:

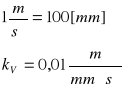
Następnie rysuję znane wektory, dzięki czemu mogę swobodnie odczytać wartości prędkości na podstawie przecięć prostych(wektorów, przy których znany jest jedynie kierunek). Długości poszczególnych odcinków oznaczają odpowiednie wartości prędkości.

Plan prędkości (w programie AutoCAD)

Z planu prędkości odczytano następujące wartości:

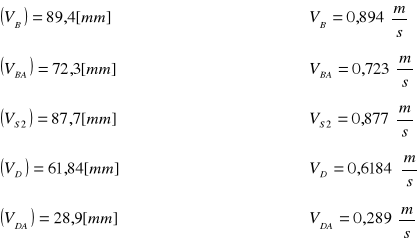
Wyznaczenie prędkości kątowej członu drugiego:

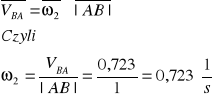
Wyznaczenie prędkości kątowej członu trzeciego:

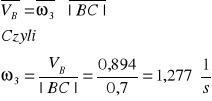
1. Grafoanalityczna analiza przyśpieszeń mechanizmu.

Przyspieszenie punktu A

Przyspieszenie członu napędzającego, podobnie jak i jego prędkość zostało z góry narzucone i wynosi:

Równania przyśpieszeń mechanizmu dla poszczególnych punktów:

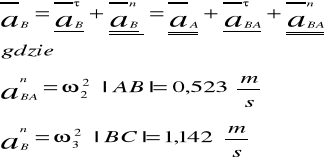
Wyznaczenie przyspieszenia pkt.D

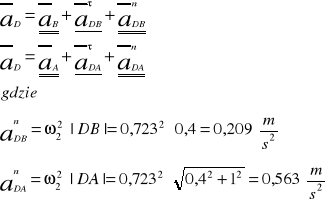
Wyznaczenie przyspieszenia pkt. środka masy S2

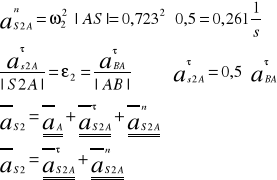
Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:

Plan przyśpieszeń

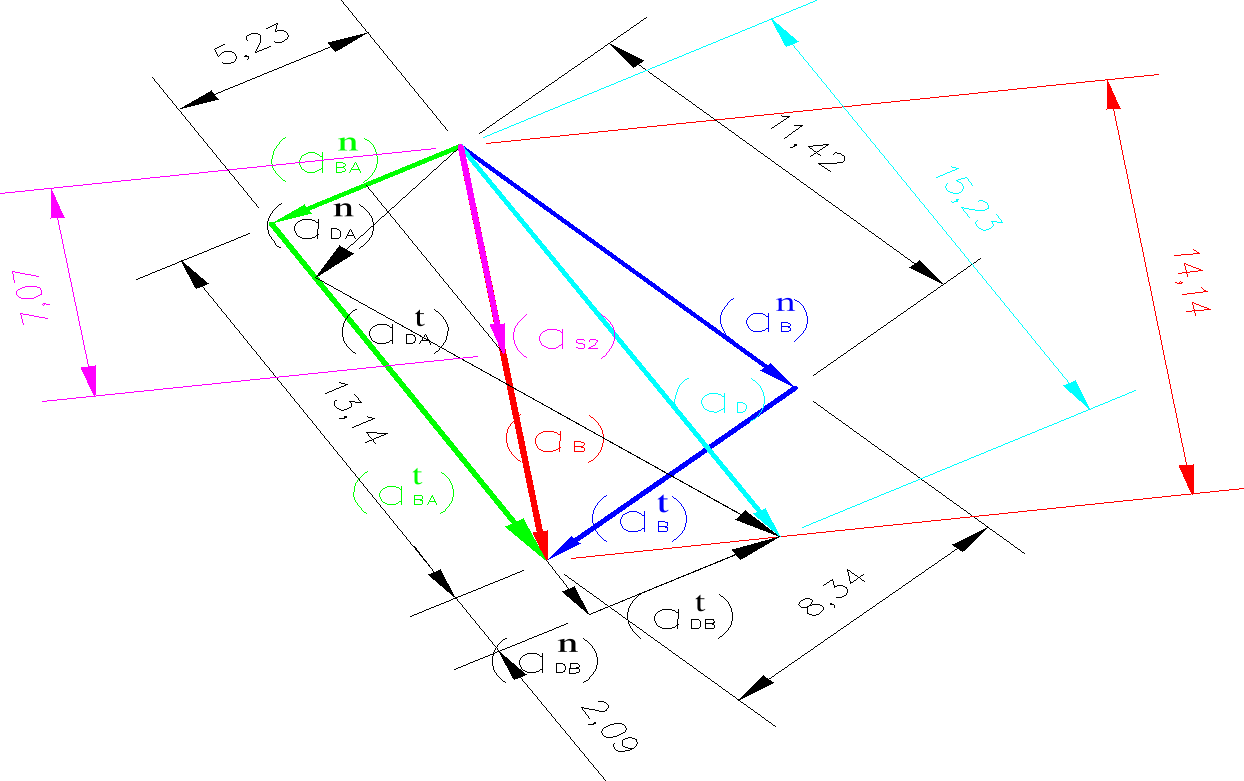
Na podstawie rysunku, analogicznie do wykresu prędkości odczytuję następujące przyspieszenia:

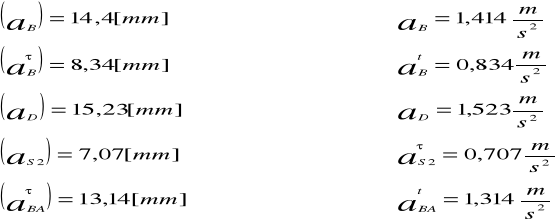
Wyznaczenie przyspieszenia kątowego członu drugiego:

Wyznaczenie przyspieszenia kątowego członu trzeciego:

1. Analiza kinematyczna mechanizmu metodą analityczną

Dane:

- φ_x(t)=0

- φ₀(t)=180

- l₀(t)= 1,956 [m]

- l₂(t)=1[m]

- l₃(t)=0,7[m]

Dodatkowo zakładam położenie początkowe:

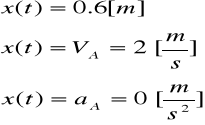
Mechanizm opisujemy wielobokiem wektorowym:

Po zrzutowaniu na osie układu mamy:

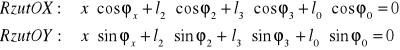
Uwzględniając fakt, iż:

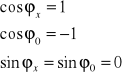
Otrzymujemy:

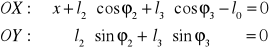
Wprowadzając oznaczenia takie jak:

Otrzymujemy:

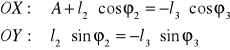
Porównując obydwie strony równania mamy:

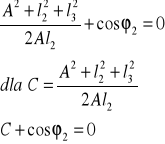
Obliczając ostatecznie współczynniki mamy:

A=-1,356

C=-0,8661

Otrzymujemy

= -30°

= 45,585°

Analityczne wyznaczanie prędkości mechanizmu.

Stosując podstawowe wiadomości z fizyki, w celu obliczenia prędkości różniczkujemy drogę po czasie.

Zarówno jak i równania drogi, tak i dla prędkości zapisujemy równania dla obydwu osi:

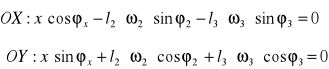
Pamiętając że:

W celu wyznaczenia prędkości
obracamy układ współrzędnych o kąt φ₃ :

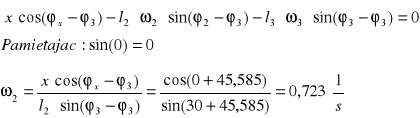
Analogicznie w celu obliczenia
przesuwamy układ współrzędnych kąt φ₂ :

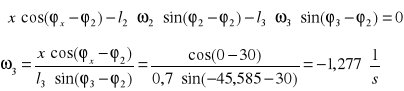
Analityczne wyznaczanie przyspieszeń mechanizmu.

Przyspieszenie jest pochodną prędkości po czasie, znając tą zależność możemy wyliczyć przyspieszenia:

Postępując tak samo, czyli obracając układ kąt
mamy:

Czyli:

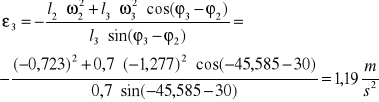
Stosując tą samą metodę wyliczamy
:

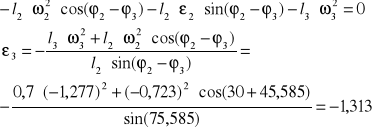
2. Wykresy analityczne w programie SAM.

Ogólny schemat w programie SAM

Powyższy schemat u uwzględnieniem toru poszczególnych punktów

Wyniki prędkości przyspieszeń w programie SAM

Porównanie otrzymanych wyników z poszczególnych metod, jako sprawdzenie poprawności obliczeń:

zmienna	metoda grafoanalityczna	metoda analityczna	SAM
Prędkości
VA	1	1	1
VB	0,894	-	0,894
VBA	0,723	-	-
VD	0,6184	-	0,619
VDA	0,289	-	-
VS2	0,877	-	0,877
ω2	0,723	0,723	0,723
ω3	1,277	-1,277	-1,277
Przyspieszenia
aA	0	0	0
aB	1,414	-	1,414
aB^t	0,834	-	-
aB^N	1,142	-	-
	1,314	-	-
	0,523	-	-
aD	1,523	-	1,522
aS2	0,707	-	0,707
ε2	1,314	-1,313	-1,314
ε3	1,19	1,19	1,19

3.0 Analiza kinetostatyczna mechanizmu.

Schemat:

Zgodnie z założeniami projektu, człon 2 mechanizmu traktujemy jako masowy. Uwzględnimy wpływ siły ciężkości na obciążenie mechanizmu.

Obliczenie momentów bezwładności:

1. założenia projektu:

przyjmuję następujące wartości siły i momentu:

P₂=20N

M₃=10m

m₂= 1 kg

Obliczam moment bezwładności na podstawie wzoru:

Wstawiając dane:

2. wyznaczenie sił bezwładności B oraz siły przyciągania G:

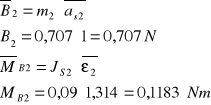
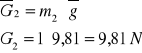
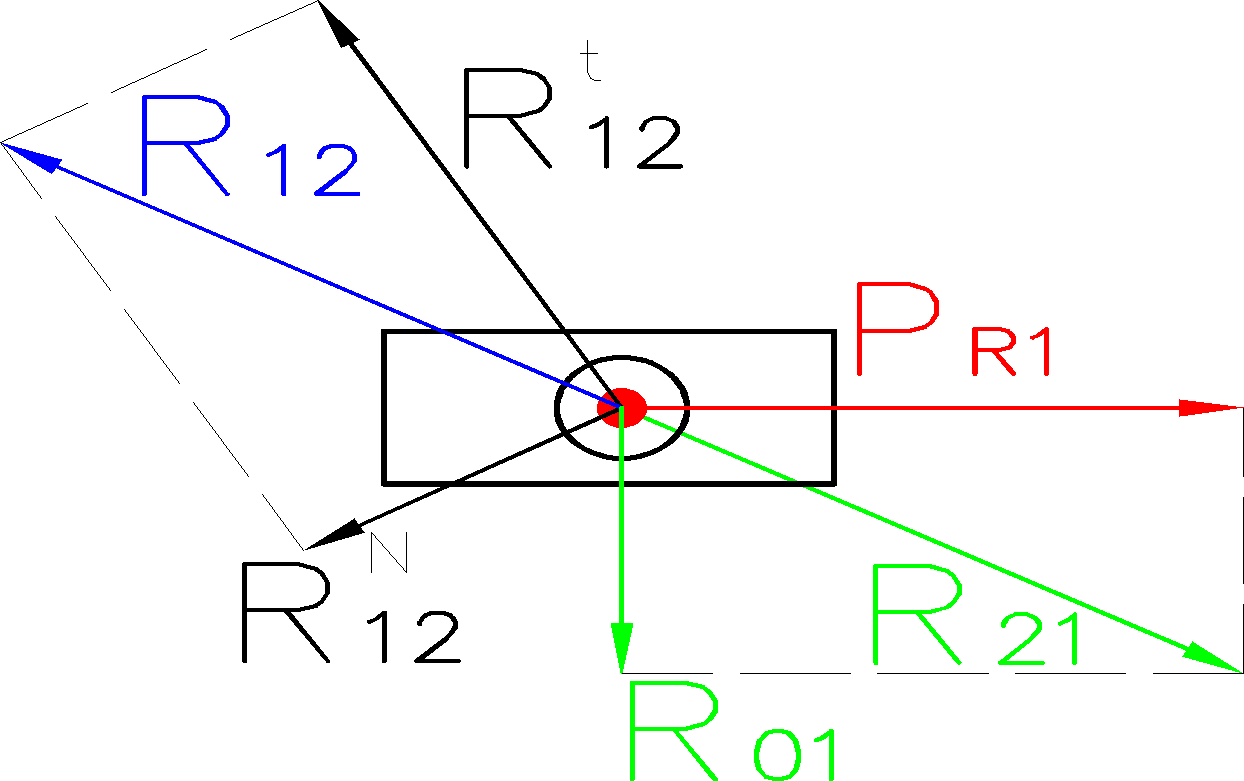
c) uwolnienie układu od więzów:

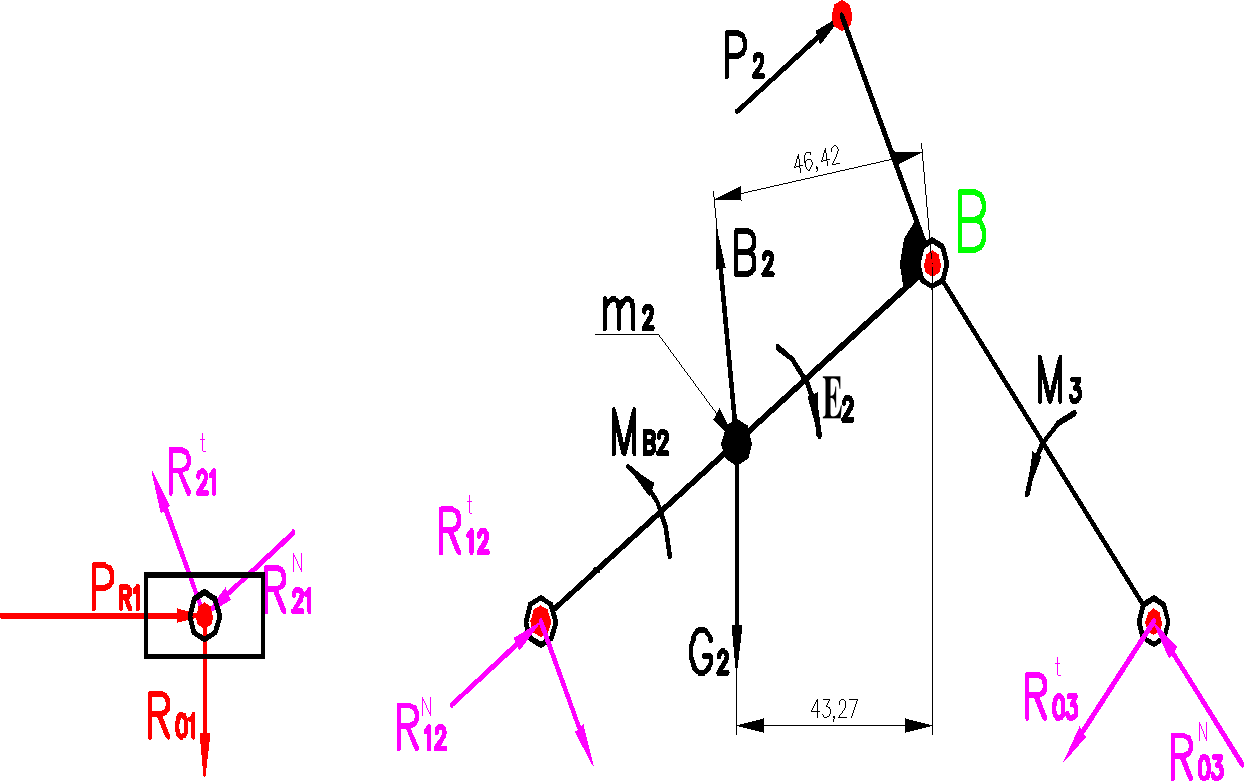
d) obliczenia sił

Ogólne równanie sił:

Równanie momentów dla członu trzeciego względem pnkt B

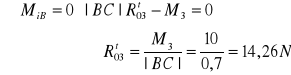
Równanie momentów dla członu drugiego względem pnkt B

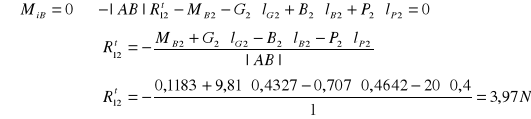
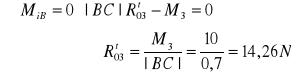
Podobnie jak to miało miejsce w przypadku metody grafoanalitycznej, teraz również posłużę się programem AutoCAD do wyznaczenia poszczególnych sił.

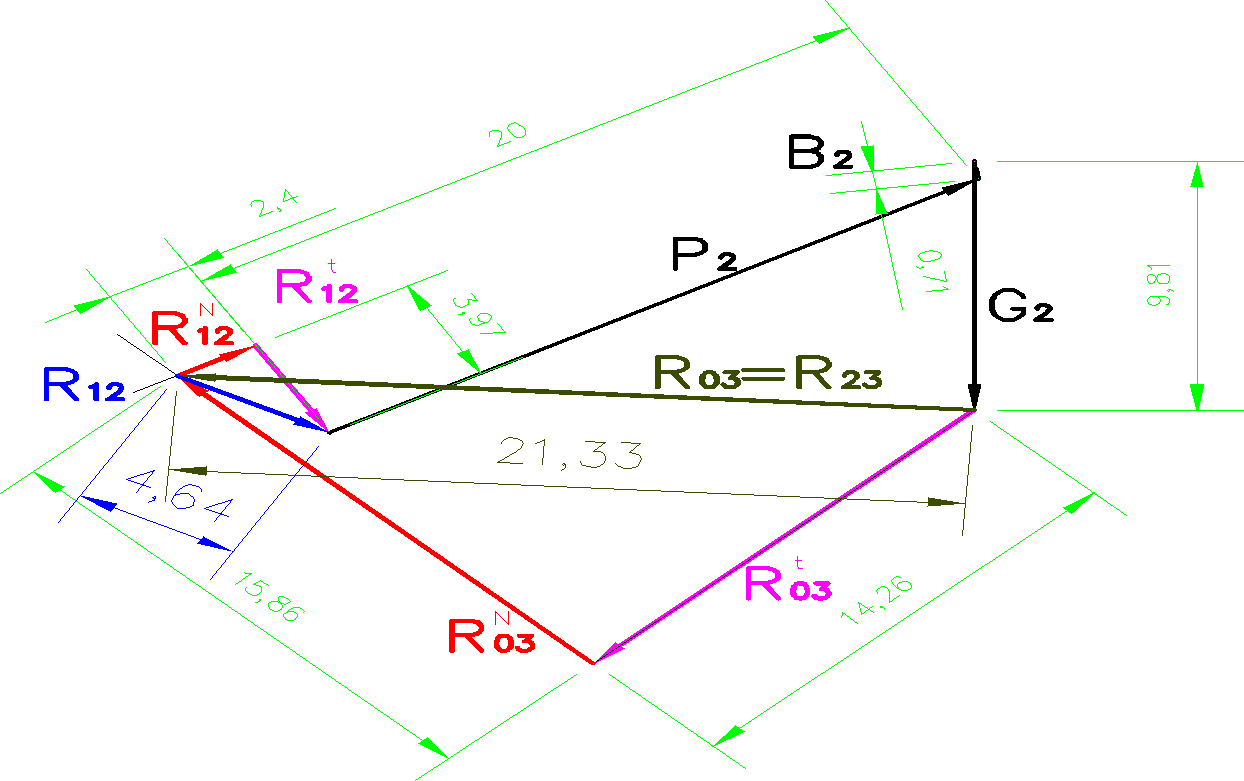
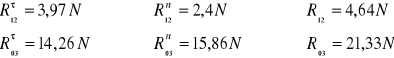
Następnie wyznaczam siły równoważącej działającej na człon napędzający:

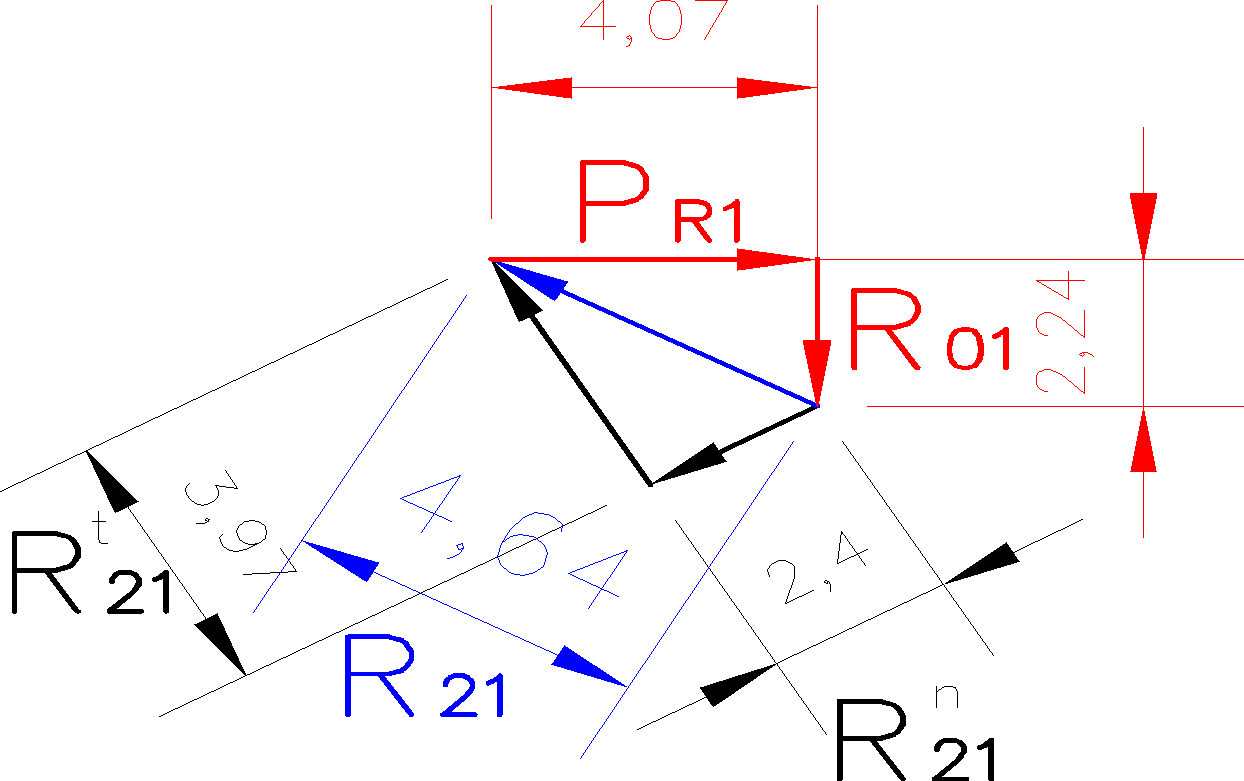
Z planu sił odczytano:

Metoda mocy chwilowej.

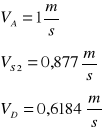
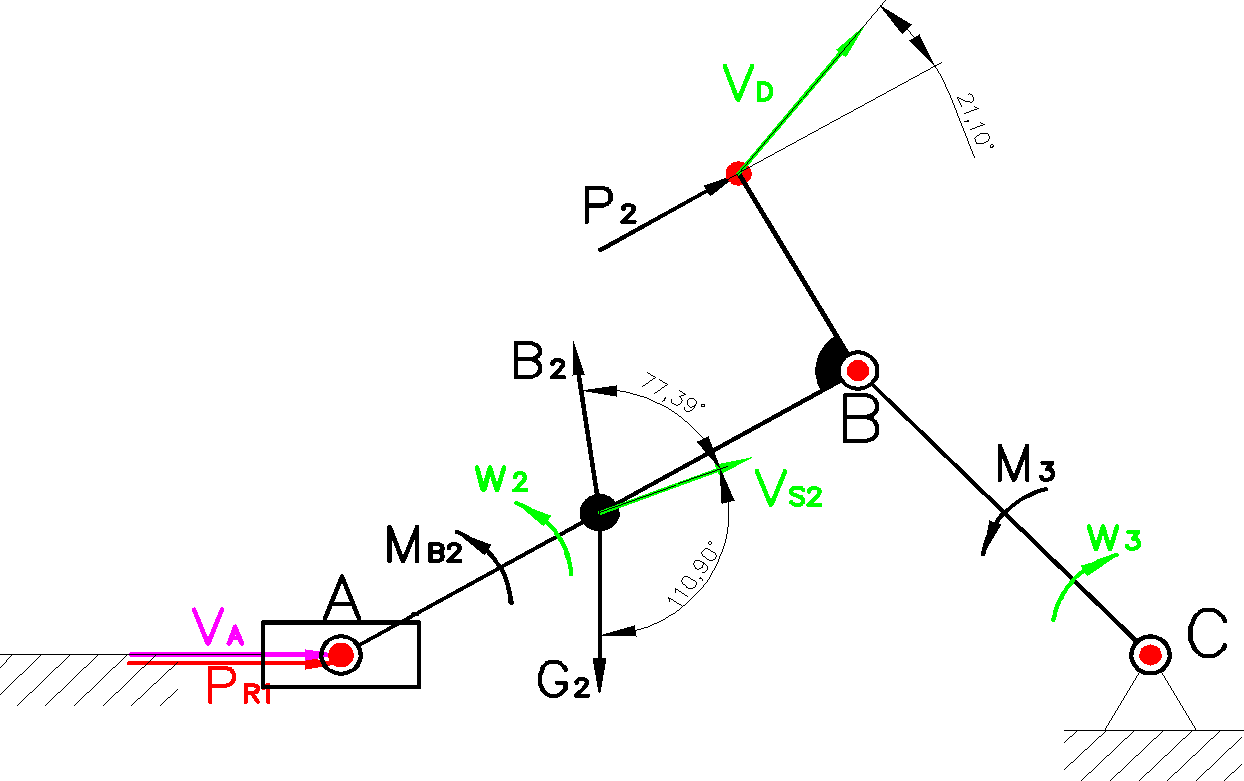
Siła równoważąca:

1. Podsumowanie analizy kinetostatycznej.

Rodzaj metody	Metoda wykreślna	Metoda mocy chwilowych	Analiza kinetostatyczna w SAM-ie
PR1	4,07	4,08	4,078




πa







PLAN SIŁ DLA CZŁONU NAPĘDZAJĄCEGO










---