Bartłomiej Tokarzewski, Krzysztof Wasikowski 10Gr
Model rywalizacji metodami numerycznymi
Pytanie: Która metoda jest dokładniejsza?
Teroria:
Model przedstawia sytuację, gdy dwa gatunki konkurują o te same ograniczone zasoby żywnościowe, czy w inny sposób hamują swój wzrost. Na przykład osobniki mogą konkurować o terytorium, pożywienie.
Rozpatrzmy dwuwymiarowy model opisujący konkurujące gatunki N1 i N2 opisany następującymi równaniami:
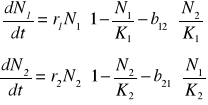
Gdzie:
N1 - populacja pierwszego gatunku, /Czerwony
N2 - populacja drugiego gatunku, /Niebieski
K1 - pojemność środowiska pierwszego gatunku,
K2 - pojemność środowiska drugiego gatunku,
r1, r2 - współczynniki liniowego wzrostu,
b12, b21 - oddziaływanie konkurencyjne.
T - czas
h - krok obliczania kolejnych przybliżeń
W wyniku konkurencji dwóch gatunków o te same zasoby jeden z nich zwykle wymiera. Poniższy wykres przedstawia wyniki dla parametrów:
K1 = 2000 osób
K2 = 1000 osób
N1 = 30 osób
N2 = 20 osób
r1 = 1.5 osób/godzine
r2 = 1.9 osób/godzine
b12 = 0.2 osób/godzine
b21 = 0.3 osób/godzine
t = 15 godzin
Dla h=1
Dla h = 0.5
Dla h = 0.1
Czerwona linia - populacja N1
Niebieska linia - populacja N2
Metoda BarTok - kółka
Metoda ODE - gwiazdki
Wnioski:
Metoda ode45(metoda Rungego-Kutty rzędu 4 i 5) jest dokładniejsza od metody BarTok.
Wyszukiwarka
Podobne podstrony:
Projekt numeryczny, IŚ Tokarzewski 27.06.2016, III semestr, Informatyka (Matlab), Projekty, Matlab -
Wszystkie pytania - Wasikowski, IŚ Tokarzewski 27.06.2016, III semestr, Meteorologia, Zaliczenie
Rachunek błędów, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (sprawozdania
sowa odp, IŚ Tokarzewski 27.06.2016, III semestr magister, Realizacja wymaganej jakości powietrza w
Zespol pomp final, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (sprawozdan
Zespol pomp, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (sprawozdania), L
opory, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, mechanika plynow XYZ, MOJE, poprawi
Filtrowanko, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (sprawozdania), L
2014.11.12 stowarzyszenie i fundacja, IŚ Tokarzewski 27.06.2016, III semestr, Hes (Podstawy prawodaw
Sprawozdanie 1 mechanika, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (spr
filtracja moja, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (sprawozdania)
sprawko metacentrum, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, mechanika plynow XYZ,
hydrologia kolos, IŚ Tokarzewski 27.06.2016, III semestr, Hydrologia, Nieposegregowane, Hydro ściąga
Reynolds Sprawozdanie 1, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Laboratoria (spra
mp pytania, IŚ Tokarzewski 27.06.2016, III semestr, Mechanika płynów, Wykłady, Egzamin, Pytania
Wzor opisu do projektu - sem mgr KJZ MS 2013, IŚ Tokarzewski 27.06.2016, III semestr magister, IKWP
więcej podobnych podstron