Poniedziałek 8⁰⁰

Wydział Górniczy	Imię i nazwisko: 1. Lucyna Szostok 2. Angelika Trawińska		Rok: II		Grupa: IV	Nr zespołu: 4
Pracowania fizyczna I	Temat: Soczewki					Nr ćwiczenia: 53
Data wykonania: 22.XI.1999.	Data oddania: 29.XI.1999.	Zwrot do poprawy:		Data oddania:		Data zal.:	Ocena:

I. Cel ćwiczenia.

Pomiar ogniskowych soczewki skupiającej i układu soczewek (skupiająca + rozpraszająca), obliczenie ogniskowej soczewki rozpraszającej oraz obserwacja i pomiar wad odwzorowań optycznych.

II. Wprowadzenie teoretyczne.

Światło widzialne stanowi małą część rozległego widma fal elektromagnetycznych różniących się między sobą długością fali . W przybliżeniu zwanym optyką geometryczną , zakłada się że długości fal są bardzo małe w porównaniu z rozmiarami urządzeń służących do ich badania , a więc można zaniedbać efekty dyfrakcyjne .

W optyce geometrycznej zakłada się , że w ośrodkach jednorodnych światło rozchodzi i się po liniach prostych. Promienie wychodzące z dowolnego punktu przedmiotu tworzą wiązkę rozbieżną. Przekształcenia tej wiązki na zbieżną, równoległą lub bardziej (mniej) rozbieżną można dokonać np. za pomocą soczewki .

Soczewką nazywamy zwykle bryłę z przezroczystego materiału , ograniczaną dwoma powierzchniami sferycznymi o promieniach R₁ i R₂

Soczewka: wymiary geometryczne, parametry optyczne

Ogniskowa soczewki określona jest następująco
:

Przyjmujemy dodatnią wartość promienia krzywizny dla powierzchni wypukłych , a ujemną dla wklęsłych wobec tego ogniskowe soczewek skupiających są dodatnie, rozpraszających ujemne .

Zależność między odległością przedmiotu , obrazu i ogniska od soczewki jest określona następująco

Związek ten wykorzystywany jest przy bezpośrednim pomiarze ogniskowej soczewek skupiających. Soczewki rozpraszające nie tworzą obrazów rzeczywistych na ekranie. Dla doświadczalnego wyznaczenia ich ogniskowych zestawia się je z soczewką skupiającą , tak by uzyskany układ optyczny wykazywał własności skupiające .

Jeżeli soczewki są blisko siebie, jest określona następującym wzorem

f₁ - ogniskowa soczewki skupiającej

f₂- ogniskowa soczewki rozpraszającej

jeżeli soczewki znajdują się w odległości d od siebie, to określamy ją wzorem

Z równań powyższych otrzymuje się wielkość ogniskowej soczewki rozpraszającej f ₂ po wstawieniu zmierzonych poprzednio wartości f i f₁ i d .

Metoda Bessela

W przypadku układu soczewek należałoby precyzyjniej określić odległość x i y ; nie jest bowiem oczywiste położenie środka optycznego. Nie zawsze pokrywa się on ze środkiem geometrycznym .

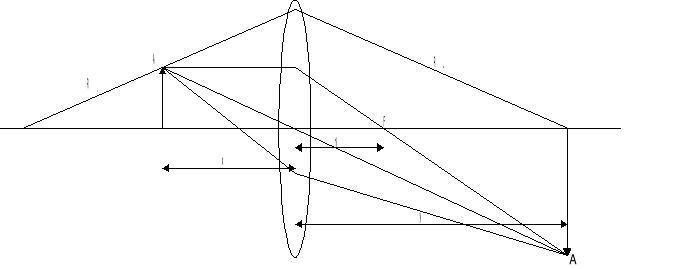
Niech l oznacza ustaloną odległość ekranu od przedmiotu świecącego. Spróbujmy określić, dla jakich położeń x soczewki na ekranie wytworzy się ostry obraz.

Zasada metody Bessela

Rozwiązując powyższy układ równań ze względu na szukaną odległość x dostajemy równanie kwadratowe

x²-lx+lf=0

Δ= l ( l - 4f )

Jeżeli l > 4f, to istnieją dwa rozwiązania :

x₁=

x₂=

Jednemu odpowiada obraz powiększony, drugiemu pomniejszony. Odległość tych położeń

d = x₂-x₁ =
.

Metoda Bessela polega na pomiarze odległości d , przy zadanym l i wyliczeniu ogniskowej f=

Wady soczewek

Wiązki światła dawane przez punkty leżące na osi optycznej układu ulegają :

Aberracji sferycznej-polega ona na tym że promienie przyosiowe są mniej odchylane niż odległe od osi skutkiem czego ich ognisko znajduje się dalej od soczewki niż promieni padających na zewnętrzne strefy soczewki,

Aberracji chromatycznej-wywołanej zjawiskiem dyspersji czyli rozszczepienia światła. Długość ogniskowej zależy od współczynnika załamania n , który jest różny dla każdej barwy światła ( więc dla każdego
),

Jeśli przedmiot punktowy leży poza osią optyczną , występują dodatkowe zniekształcenia:

koma - obraz punktu świecącego na kształt krążka z ogonem, przypominający przecinek (łac. coma) lub kometę

astygmatyzm - wiązka padająca skośnie na środek soczewki nie daje w ogóle obrazu punktowego, lecz w dwóch odpowiednich położeniach ekranu jasne odcinki pionowy i poziomy

zakrzywienie pola obrazu - punkty składające się na obraz powierzchni płaskiej prostopadłej do osi optycznej nie leżą w płaszczyźnie prostopadłej do osi optycznej.

III. Wyniki pomiarów i obliczeń

1.Wyznaczenie ogniskowej soczewki skupiającej

Metoda bezpośrednia

l [cm]	x [cm]	y=l-x [cm]	f [cm]	fśr [cm]
90	76,5	12,8	11,00	11,37
95	81,5	13,5	11,58
98	85,0	13,0	11,27
102	89,0	13,0	11,34
105	92,0	13,0	11,39
110	97,0	13,0	11,46

Metoda Bessela

l [cm]	x1 [cm]	x2 [cm]	f [cm]	fśr [cm]
110	91,50	12,50	13,32	13,17
105	87,00	12,90	13,18
100	82,00	13,10	13,13
95	76,00	13,60	13,50
90	70,50	14,00	13,16
85	64,00	14,20	12,74

Odchylenia standardowe średniej dla obu metod pomiaru

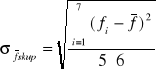
= 0,08[cm] dla metody bezpośredniej

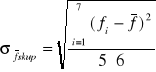
= 0,10[cm] dla metody Bessela

Zatem:

dla metody bezpośredniej = 11,370,08 [cm]

dla metody Bessela = 13,170,10 [cm]

2.Wyznaczenie ogniskowej układu soczewek

l [cm]	x1 [cm]	x2 [cm]	f [cm]	fśr [cm]
90	15,00	50,00	19,10	19,53
95	14,20	52,30	19,93
100	13,80	56,60	20,42
105	13,20	61,20	20,76
110	12,80	66,70	20,90
113	12,50	77,20	18,99
116	12,00	82,50	18,28
120	11,70	88,00	17,87

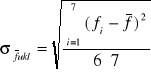
= 0,4[cm]

Zatem:

f_układu = 19,530,4 [cm]

3.Wyznaczenie ogniskowej soczewki rozpraszającej

Jeżeli soczewki są ustawione w odległości δ od siebie, to ogniskową układu wyznacza się ze wzoru

Ogniskową soczewki rozpraszającej liczymy z powyższego wzoru traktując jako znane ogniskową układu i soczewki rozpraszającej.

Przekształcenia prowadzą do wzoru:

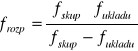
Zatem

f_rozp = 40,41 [cm]

Oszacowanie błędu Δf_rozp

Prawo przenoszenia błędów

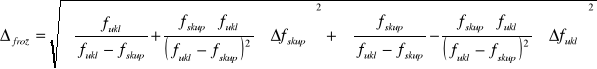
0,10[cm]

0,40[cm]

f_skup = 13,170,15 [cm]

f_ukł = 19,530,4 [cm]

1,74 [cm]

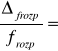
4,30 %

4.Badanie wad soczewek

a)Aberracja sferyczna

	l [cm]	x1 [cm]	x2 [cm]	d=x1-x2 [cm]	f [cm]	fśr [cm]
Promienie brzegowe	105	74,00	22,00	52,00	19,81	20,05
		100	69,50	23,50	46,00		19,71
		95	63,00	25,00	38,00		19,95
		90	55,00	26,60	28,40		20,26
		85	50,00	34,50	15,50		20,54
	Promienie środkowe	100	76,00	25,00	51,00		18,49	19,30
		96	70,00	26,30	43,70		19,02
		90	63,00	29,50	33,50		19,38
		86	57,00	32,00	25,00		19,68
		82	49,00	35,00	14,00		19,90

Miarą aberracji sferycznej jest różnica ogniskowych dla promieni brzegowych i przyosiowych:

Δ_s = _p.brz - _p.śr = 0,75 [cm]

= 0,15cm]

= 0,45[cm]

b) aberracja chromatyczna

	L [cm]	x1 [cm]	x2 [cm]	d=x1-x2 [cm]	f [cm]	fśr [cm]
Światło czerwone	107	82,00	21,90	60,10	18,31	18,82
		110	85,50	22,60	62,90		18,51
		112	87,50	23,50	64,00		18,86
		94	65,00	26,00	39,00		19,45
		97	70,00	24,80	45,20		18,98
	Światło fioletowe	87	56,00	25,50	30,50		19,07	18,79
		90	59,00	25,00	34,00		19,28
		96	68,00	24,30	43,70		19,02
		104	79,00	23,90	55,10		18,70
		110	86,00	21,00	65,00		17,89

Miarą aberracji chromatycznej jest różnica ogniskowych dla promieni czerwonego i fioletowego.

Δ_ch = _cz - _fiol = 0,02 [cm]

= 0,22[cm]

= 0,65[cm]

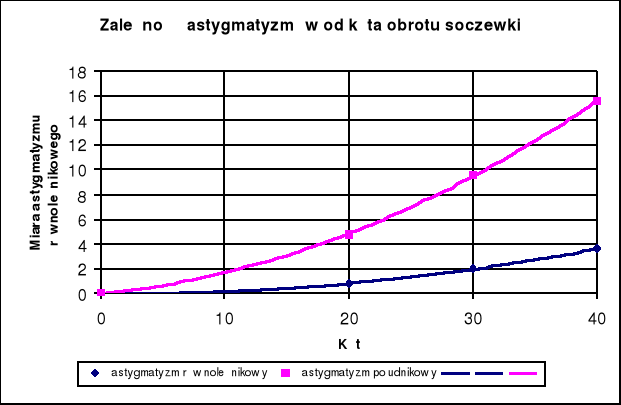
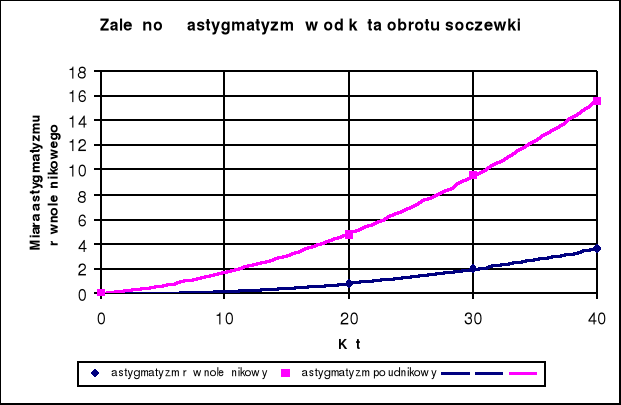
5.Astygmatyzm.

Wykres zależności x_r-x₀ oraz x_p-x₀ od kąta α dla astygmatyzmu soczewki.

IV. Wnioski:

Wyniki otrzymane w obu metodach różnią się, w metodzie bezpośredniej wyznaczyłyśmy ogniskową z większą dokładnością (mniejsza wartość odchylenia standardowego średniej). Wartości nie są równe w granicach błędu.

W porównaniu różnicy ogniskowych będącej miarą aberacji sferycznej do wartości błędów wyznaczonych ogniskowych widzimy, że różnica ta jest większa niż błędy. W przypadku aberacji chromatycznej różnice ogniskowych są mniejsze od błędów pomiarów tych ogniskowych. Pomiary są wystarczająco dokładne, aby zauważyć aberrację sferyczną, natomiast chromatyczną nie.

Z wykresu można zaobserwować, iż astygmatyzm zależy wykładniczo od kąta skręcenia soczewki w stosunku do promienia padającego na nią. Astygmatyzm południkowy bardziej zależy od kąta niż astygmatyzm równoleżnikowy.

---