Liniowe modele decyzyjne

1. Przykłady modeli. Struktura modeli decyzyjnych.

Przykład 1.1

Przedsiębiorstwo wytwarza dwa wyroby W₁ i W₂. Dane są informacje dotyczące:

• zapotrzebowania dziennego na wyroby przedsiębiorstwa,

• pracochłonności,

• zużycia materiału,

• zysku netto ze sprzedaży wyrobów.

Wyszczególnienie	Jednostka miary	Wyrób W1	Wyrób W2
Zapotrzebowanie dzienne na wyroby W1 i W2	Jednostka wyrobu	1000	2000
Pracochłonność	roboczogodz./jed. wyrobu	3	6
Zużycie materiału	kg/jed. wyrobu	18	6
Wynik netto ze sprzedaży	zł/jed. wyrobu	18	12

Efektywny dzienny fundusz czasu pracy w przedsiębiorstwie wynosi 24 000 roboczo - godzin. Dzienne zużycie materiału nie może przekroczyć 45 ton.

Określić taki plan produkcji przedsiębiorstwa, tak aby zapotrzebowanie odbiorcy było zaspokojone a zysk netto ze sprzedaży wyrobów W₁ i W₂ był maksymalny.

Niech x₁ oznacza planowaną wielkość produkcji wyrobu W₁ a x₂ wielkość produkcji wyrobu W₂.

Warunki brzegowe:

x₁ ≥ 1000, x₂ ≥ 2000.

Warunki wewnętrznej zgodności:

3x₁ +6x₂ ≤ 24.000,

18x₁ +6x₂ ≤ 45.000.

Funkcja celu: Z(x₁, x₂) = 18x₁ + 12x₂.

Przykład 1.2.

Dwie linie komunikacji miejskiej mogą być obsługiwane przez trzy rodzaje środków transportu: trolejbusy, autobusy i tramwaje. Dane o dziennej zdolności przewozowej, dziennych kosztach eksploatacji, okresie eksploatacji środków transportu i przewidywanej wielkość pracy poniżej:

Rodzaj środka transportu	Dzienna zdolność przewozowa [tys. pasażero-km] na linii		Dzienne koszty eksploatacji [tys. zł] na linii		Okres eksploatacji [doby]
		1	2	1		2
Trolejbusy Autobusy Tramwaje	10 5 12	15 10 10	4 3 5	8 4 4	300 300 300
Planowana wielkość pracy Transportowej [tys. pasażero - km]	3600	4800

Należy opracować plan przydziału środków transportu dla obu linii komunikacji miejskiej, przyjmując jako kryterium optymalizacji, minimum kosztów eksploatacji.

Zmienne decyzyjne: X = [x_ij], /i=1,2,3; j=1,2/, x_ij oznacza tę część okresu eksploatacji , którym środek transportu „i-tego” rodzaju przeznaczony jest do eksploatacji na „j - tej” linii.

Warunki brzegowe: x_ij ≥ 0 oraz x₁₁ + x₁₂ ≤ 1,

x₂₁ + x₂₂ ≤ 1,

x₃₁ + x₃₂ ≤ 1.

Warunki wewnętrznej zgodności: na linii nr 1: 300 (10x₁₁ + 5x₂₁ + 12x₃₁) = 3600,

na linii nr 2: 300 (15x₁₂ + 10x₂₂ + 10x₃₂) = 4800.

Funkcja celu: K (x_ij) = 300 (4x₁₁ + 8x₁₂ + 3x₂₁ + 4x₂₂ + 5x₃₁ + 4x₃₂).

Przykład 1.3

Do montażu trzech różnych urządzeń U₁, U₂ oraz U₃ potrzebne są trzy podzespoły P₁, P₂ oraz P₃.Zasób podzespołów P oraz liczba podzespołów niezbędna do montażu urządzeń U_i w tabeli poniżej:

Podzespół	Jednostka montażowa	Urządzenia			Zasób podzespołów
				U1		U2	U3
P1 P2 P3	[sztuki]	3 1 3	2 4 3	0 0 1	10 11 13
	Zysk jednostkowy [tys. zł]	4	5	1

Opracować dzienny plan montażu wymienionych urządzeń, przyjmując jako kryterium optymalizacji zysk łączny ze sprzedaży urządzeń U₁, U₂ i U₃.

Zmienne decyzyjne: X = [x_i], /i = 1,2,3/, x_i - liczba zmontowanych urządzeń U_i.

Warunki brzegowe:

x_i ≥ 0 i x_i przyjmują tylko wartości naturalne /tzw. optymalizacja całkowitoliczbowa/

Warunki wewnętrznej zgodności:

3x₁ + 2x₂ + 0x₃ ≤ 10,

1x₁ + 4x₂ + 0x₃ ≤ 11,

3x₁ + 3x₂ + 1x₃ ≤ 13.

Funkcja celu: F(x₁, x₂, x₃) = 4x₁ + 5x₂ + 1x_3.

Rzeczywiste sytuacje decyzyjne mogą wymuszać jednoczesną realizacje dwu celów, z których jeden jest maksymalizacją funkcji celu F₁, drugi natomiast minimalizacją funkcji F₂. w takim przypadku rozwiązaniem skutecznym jest zdefiniować funkcję F, która jest ilorazem danych funkcji F₁ i F₂.

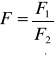
Ponieważ chcemy określić maksimum funkcji F₁ i minimum funkcji F₂, stąd funkcja F przyjmie wartość maksymalną. Tak określony problem nazywany jest optymalizacją zagadnienia z wymierną funkcją celu.

Przykład 1.4

Przedsiębiorstwo na dwu urządzeniach A oraz B wytwarza dwa wyroby W₁ i W₂. Obydwa wyroby sprzedawana są za granicę. Dane o zużyciu materiału, pracochłonności, kosztach jednostkowych produkcji, cenie w sprzedaży eksportowej oraz poziomie minimalnego zapotrzebowania odbiorcy poniżej:

Dane	Jednostki	Wyrób		Zasoby [tys. jed.]
					W1	W2
Zużycie materiału na jednostkę wyrobu	[kg]	3	2	6
Pracochłonność na jednostkę wyrobu dla urządzenia A	[maszyno /godz.]	6	3	9
Pracochłonność na jednostkę wyrobu dla urządzenia B	[maszyno /godz.]	4	4	8
Koszt jednostkowy Produkcji	[PLN]	100	80
Cena sprzedaży w eksporcie	[PLN]	155	139
Minimalne zapotrzebowanie odbiorcy	[tys. kg]	0,5	0,5

Opracować taki plan produkcji wyrobów W₁ oraz W₂, który zapewnia uzyskanie największych wpływów ze sprzedaży eksportowej przy najmniejszych kosztach produkcji.

Niech x₁ oznacza skalę produkcji wyrobu W₁ a x₂ skalę produkcji wyrobu W₂.

Warunki brzegowe: x₁ ≥ 0.5, x₂ ≥ 0.5,

Warunki wewnętrznej zgodności:

3x₁ + 2x₂ ≤ 6,

6x₁ + 3x₂ ≤ 9,

4x₁ + 4x₂ ≤ 8.

Koszt łączny jest równy: K(x₁, x₂) = 100x₁ + 80x₂,

Wpływ łączny ze sprzedaży /brutto/ W(x₁, x₂) = 155x₁ + 139x₂,

Funkcja celu: min (Z(x₁, x₂) =
).

2. Rozwiązania modeli

1. Rozwiązania dopuszczalne

Rozwiązanie modelu programowania liniowego jeśli istnieje, jest rozwiązaniem wyznaczanym przez warunki wewnętrznej zgodności. Rozwiązanie takie może istnieć tylko wówczas, gdy zbiór rozwiązań warunków wewnętrznej zgodności nie jest zbiorem pustym. Jeśli zatem rozwiązanie takie istnieje, oznacza to, iż został zidentyfikowany zbiór decyzji dopuszczalnych zagadnienia.

Brak rozwiązań dopuszczalnych wynika z dwu przyczyn Pierwsza, dotyczy zwykle sytuacji w której warunki wewnętrznej zgodności są wzajemnie sprzeczne. Oznacza to, iż definiując ograniczenia nie ustrzegliśmy się błędów. Druga przyczyna braku rozwiązań dopuszczalnych jest rezultatem pominięcia ważnych dla zagadnienia relacji bądź ograniczeń.

Jeśli zbiór warunków wewnętrznej zgodności ma rozwiązanie niezerowe, to jest to wielościan wypukły w przestrzeni n+1 wymiarowej. Przez wypukłość wielościanu należy rozumieć taką jego właściwość, że odcinek łączący dwa dowolne punkty należące do wielościanu należy także do tego wielościanu.

Tw.1 Zbiór rozwiązań dopuszczalnych liniowego modelu decyzyjnego jest zbiorem wypukłym.

A B

D - zbiór pusty D - zbiór jednoelementowy

D - zbiór wieloelementowy D - zbiór wieloelementowy

ograniczony nieograniczony

Przykłady zbiorów rozwiązań dopuszczalnych w przestrzeni dwuwymiarowej

Def. 2.1.1. Bazowym rozwiązaniem dopuszczalnym modelu liniowego jest takie rozwiązanie dopuszczalne, w którym składowe wektora X = {x₁, x₂, … ,x_n}, x_i są nieujemne, natomiast wektor niegazowy X, to wektor którego składowe x_i = 0.

Def. 2.1.2. Nie zdegenerowanym dopuszczalnym rozwiązaniem bazowym nazywamy takie rozwiązanie bazowe, w którym wszystkie elementy wektora bazowego są dodatnie. Jeżeli co najmniej jedna składowa x_i wektora X jest równa zero, to takie rozwiązanie bazowe dopuszczalne definiujemy jako zdegenerowane.

2. Rozwiązanie optymalne

Rozwiązanie optymalne ma szczególne własności. Pierwsza niezwykle istotna to ta, iż rozwiązanie optymalne jest jednym z rozwiązań dopuszczalnych. Stąd oczywisty wniosek, zbiór rozwiązań dopuszczalnych nie może być zbiorem pustym. Druga własność rozwiązania optymalnego związana jest z procedurą wyboru takiego rozwiązania. Kryterium wyboru określa funkcja celu. Kolejna własność dotyczy liczby rozwiązań optymalnych - jeśli funkcja kryterium osiąga ekstremum dla dwu rożnych rozwiązań to zagadnienie takie ma ich nieskończenie wiele:

F(X⁰) = F(X¹), gdzie: X⁰ ={x₁⁰,x₂⁰,…,x_n⁰}, X¹ = {x₁¹,x₂¹,…,x_n¹}.

To dowolny wektor X można zdefiniować jako kombinację liniową wektorów X⁰ i X¹:

X = αX⁰ +(1-α)X¹, stąd F(X) = αF(X⁰) +(1-α)F(X¹) gdzie: α € [0,1].

Def. 2.2.1 Optymalnym rozwiązaniem bazowym nazywamy takie bazowe rozwiązanie dopuszczalne, które maksymalizuje (minimalizuje) funkcję celu.

Tw. 2 Funkcja celu osiąga wartość optymalną w punkcie wierzchołkowym wielościanu wypukłego D, będącego zbiorem rozwiązań dopuszczalnych.

3. Metody rozwiązań modeli decyzyjnych

1. Metoda geometryczna

Rozważmy Przykład 1.1 z dwoma zmiennymi decyzyjnymi {x₁, x₂}:

Warunki brzegowe:

x₁ ≥ 1000, x₂ ≥ 2000.

Warunki wewnętrznej zgodności:

3x₁ +6x₂ ≤ 24.000,

18x₁ +6x₂ ≤ 45.000.

Funkcja celu: max{Z(x₁, x₂) = 18x₁ + 12x₂}.

Obrazem graficznym warunków wewnętrznej zgodności są półpłaszczyzny o równaniach:

3x₁ +6x₂ ≤ 24.000,

18x₁ +6x₂ ≤ 45.000.

Uwzględniając warunki brzegowe, można graficznie opisać zbiór rozwiązań dopuszczalnych:

x₂

A(1000,2000), Z(1000,2000) = 42.000,00,

B(1000,3500), Z(1000,3500) = 60.000,00,

C(1400,3300), Z(1400,3300) = 64.800,00

D(1833.(3),2000), Z(1833,(3),2000) = 57.999,99.

B

C

D

A

x₁

Funkcja celu osiąga maksimum równe 64.800,00 dla x₁=1400, x₂=3300. Rozwiązanie to otrzymane przy wykorzystaniu prostych narzędzi jest ograniczone do przypadku dwu zmiennych decyzyjnych, przypadek większej liczby zmiennych aniżeli dwie, wymaga stosowania bardziej złożonych metod.

2. Metoda simplex.

W omówionych modelach, zauważamy cech wspólne, wynikające z warstwy strukturalnej modelu. Są to, warunki brzegowe, warunki wewnętrznej zgodności oraz funkcja celu. Uogólniając, każde zagadnienie programowania liniowego można zapisać jako:

Zbiór warunków brzegowych:

x₁, x₂,…x_n ≥ 0,

Zbiór warunków wewnętrznej zgodności:

a₁₁x₁+a₁₂x₂+…+a_1nx_n ≤ b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n ≤ b₂

(3.2.1) …………………………

a_m1x₁+a_m2x₂+…+a_mnx_n ≤ b_m

Jest to postać standardowa modelu liniowego.

Kierunek nierówności może być przeciwny.

Funkcja celu:

max {F(x₁, x₂,…x_n) = c₁x₁ + c₂x₂ + … +c_nx_n}

x_i

Układ warunków (3.2.1) można przedstawić jako układ równań, wystarczy wprowadzić po prawej stronie nierówności takie nieujemne y_j, /j=1,2,…m/ takie że:

y₁ = -(a₁₁x₁+a₁₂x₂+…+a_1nx_n) + b₁

y₂ = -(a₂₁x₁+a₂₂x₂+…+a_2nx_n) + b₂

(3.2.2) …………………………

y_m = -(a_m1x₁+a_m2x₂+…+a_mnx_n) + b_m

Jest to postać kanoniczna modelu liniowego i dalej:

y₁ = a₁₁(-x₁)+a₁₂(-x₂)+…+a_1n(-x_n) + b₁

y₂ = a₂₁(-x₁)+a₂₂(-x₂)+…+a_2n(-x_n) + b₂

(3.2.3) …………………………

y_m = a_m1(-x₁)+a_m2(-x₂)+…+a_mn(-x_n) + b_m

Funkcja celu:

max {F(x₁, x₂,…x_n) = (-c₁)(-x₁) + (-c₂)(-x₂) + … +(-c_n)(-x_n)}.

x_i

Zadanie tak sformułowane zostało rozwiązane po raz pierwszy w 1949 roku przez matematyka amerykańskiego J. Dantziga. W teorii badań operacyjnych rozwiązanie to znane jest pod nazwą „metody simplex”.

	-x1	-x2	...	-xs	...	-xj	...	-xn	B
y1	a11	a12	...	a1s	…	a1j	…	a1n	B1
y2	a21	a22	...	a2s	…	a2j	…	a2n	B2
…….	…….	…….	...	…….	…	…….	…	…….	…….
yr	ar1	ar2	...	ars	…	arj	…	arn	br
…….	…….	…….	...	…….	…	…….	…	…….	…….
yi	ai1	ai2	...	ais	...	aij	...	ain	bi
…….	…….	…….	...	…….	…	…….	…	…….	…….
ym	am1	am2	...	ams	...	amj	...	amn	bm
Z	-c1	-c2	...	-cs	…	-cj	…	-cn	Z0

Rozwiązanie modelu metodą simplex początkuje wybór dowolnego rozwiązania bazowego /określonego przez współrzędne wierzchołka należącego do zbioru rozwiązań dopuszczalnych/ a następnie rozwiązanie to zostaje „poprawione” zgodnie z treścią oczekiwań zawartych w definicji funkcji celu /jest to równoznaczne z oznaczeniem współrzędnych któregoś z wierzchołków zbioru rozwiązań dopuszczalnych/. Nie jest to wybór przypadkowy, lecz taki, który gwarantuje większą /mniejszą/ wartość funkcji celu aniżeli w przypadku poprzednio otrzymanego rozwiązania bazowego. Drogę po jakiej „przenoszone” jest rozwiązanie bazowe, wskazuje tzw. element rozwiązujący.

Schemat wyboru elementu rozwiązującego:

Typ optimum
max	min

Czy w wierszu Z są Elementy ujemne?

Czy w wierszu Z są Elementy dodatnie?

tak tak

Jako kolumnę rozwiązującą wybrać kolumnę z najmniejszym ujemnym elementem w wierszu Z

nie

Otrzymane rozwiązanie bazowe jest rozwiązaniem optymalnym

Nie

Jako kolumnę rozwiązującą wybrać kolumnę z największym dodatnim elementem w wierszu Z

Dla każdego dodatniego elementu /oprócz elementu w wierszu Z/ kolumny rozwiązującej, obliczyć iloraz: elementu z kolumny wyrazów wolnych znajdującego się danym wierszu przez element kolumny rozwiązującej znajdujący się w tym wierszu.

Jako wiersz rozwiązujący przyjąć wiersz, któremu odpowiada najmniejszy iloraz.

Załóżmy, że a_rs jest elementem rozwiązującym, oznacza to konieczność zmiany rozwiązania bazowego, składowe y_r oraz x_s „wymieniają się” miejscami w tablicy simplex. W nowym rozwiązaniu bazowym zmieniają się wartości składowych wektora b_j, wektora c_i oraz współczynniki a_ij.

Wzory „przejścia” do nowego rozwiązania bazowego:

Element rozwiązujący: a^k_rs =
,

Elementy kolumny rozwiązującej: a^k_is = -
, i≠r, c^ks = -
,

Elementy wiersza rozwiązującego: a^k_rj =
, j≠s, b^k_r =
,

Elementy leżące poza wierszem oraz kolumną rozwiązującą z wyjątkiem kolumny „b” oraz wiersza „Z”:

a^k_ij =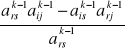
, i≠r, j≠s,

Elementy w wierszu „Z” poza kolumną rozwiązującą:

c^k_j =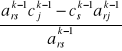
, j≠s,

Elementy w kolumnie „b” poza wierszem rozwiązującym:

b^k_i =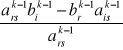
, i≠r,

Wartość funkcji celu Z₀:

Z^k₀ =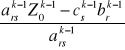
.

Procedura wyznaczania rozwiązania optymalnego metodą simplex jest zbiorem powtarzalnych iteracji. Kiedy to po zdefiniowaniu pierwszego bazowego rozwiązania, które jest rozwiązaniem dopuszczalnym następuje „poprawianie” rozwiązania w kolejnych iteracjach, indeks „k” oznacza kolejna iterację.

Kiedy rozwiązanie dopuszczalne jest rozwiązaniem najlepszym? Obowiązują dwie zasady, zależą one od typu ekstremum funkcji celu:

1. Maksimum funkcji celu: jeżeli po zakończeniu „k” iteracji wszystkie elementy kolumny „b” oraz wiersza „Z” są nieujemne, to rozwiązanie optymalne otrzymujemy, przyrównując zmienne decyzyjne w pierwszym wierszu do zera, a zmienne decyzyjne pierwszej kolumny przyrównujemy do elementów kolumny „b”.

2. Minimum funkcji celu: jeżeli po zakończeniu „k” iteracji wszystkie elementy kolumny „b” są nieujemne a wszystkie elementy wiersza „Z” ujemne, to rozwiązanie optymalne otrzymujemy, przyrównując zmienne decyzyjne w pierwszym wierszu do zera, a zmienne decyzyjne pierwszej kolumny przyrównujemy do elementów kolumny „b”.

4. Modele dualne

Dany model decyzyjny zagadnienia programowania liniowego:

Zbiór warunków brzegowych:

x₁, x₂,…x_n ≥ 0,

Zbiór warunków wewnętrznej zgodności:

a₁₁x₁+a₁₂x₂+…+a_1nx_n ≤ b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n ≤ b₂

(4.1) …………………………

a_m1x₁+a_m2x₂+…+a_mnx_n ≤ b_m

Jest to postać standardowa modelu liniowego.

Kierunek nierówności może być przeciwny.

Funkcja celu:

max {F(x₁, x₂,…x_n) = c₁x₁ + c₂x₂ + … +c_nx_n}

x_i

Niech U = {u₁,u₂, ,u_m}.

Ponadto zmienne u_j spełniają warunki:

a₁₁u₁+a₂₁u₂+…+a_m1u_m ≥ c₁

a₁₂u₁+a₂₂u₂+…+a_m2u_m ≥ c₂

(4.2) …………………………

a_1nu₁+a_2nu₂+…+a_mnu_m ≥ b_m

Funkcja celu:

min {G(u₁, u₂,…,u_m) = b₁u₁ + b₂u₂ + … +b_mu_m}

u_i

Układ warunków (4.2) oraz funkcja celu G(U) są obrazem pewnej sytuacji decyzyjnej w strukturze której występują elementy modelu (4.1). W literaturze przyjęto obydwa modele określać jako dualne.

5. Rozwiązanie modelu decyzyjnego a rozwiązanie modelu dualnego

Ciekawe w jakiej relacji pozostają do siebie rozwiązania obydwu zagadnień? W definicji rozwiązania optymalnego modelu dualnego kierujemy się tezami trzech twierdzeń:

Tw. 5.1. Jeżeli jedno z zagadnień dualnych ma rozwiązanie optymalne, to rozwiązanie optymalne ma również drugie zagadnienie, przy czym dla dowolnych rozwiązań optymalnych zachodzi relacja:

Z_max(X) = G_min(U).

Tw. 5.2. Wartość optymalna zmiennej decyzyjnej u_j zadania dualnego określa przyrost wartości funkcji celu Z_max przy zmianie ograniczenia b_j o jednostkę:

u_j = ∆(
).

Z tezy Tw 5.2. wynika, że zmienna u_j zagadnienia dualnego określa, o ile zmienia się maksymalna wartość funkcji celu zagadnienia pierwotnego, jeżeli odpowiednie ograniczenie zmienia się o jednostkę. Im większa wartość u_j, tym większy wpływ „j” ograniczenia na wartość funkcji celu.

Tw. 5.3. Jeżeli dla optymalnego rozwiązania zagadnienia pierwotnego lub dualnego, jedno z ograniczeń jest nierównością ostrą, to w każdym optymalnym rozwiązaniu zagadnienia dualnego do niego odpowiadająca temu ograniczeniu zmienna decyzyjna przyjmuje wartość równą zero. Natomiast jeżeli jedna ze zmiennych w rozwiązaniu optymalnym przyjmuje wartość dodatnią, to odpowiadające jej ograniczenie jest równością.

6. Analiza wrażliwości rozwiązania optymalnego.

Zdefiniowanie rozwiązania optymalnego prowokuje do kolejnych pytań: jak zmieni się rozwiązanie optymalne jeśli zmienią się parametry funkcji celu, jak zmieni się takie rozwiązanie jeśli ulegną zmianie ograniczenia warunków wewnętrznej zgodności?, w jakim przedziale mogą zmieniać się parametry funkcji celu a także ograniczenia warunków wewnętrznej zgodności bez wpływu na postać rozwiązania optymalnego?.

Przykład 6.1

Przeanalizujmy ponownie Przykład 1.1, próbując odpowiedzieć na dwa poniżej sformułowane pytania:

1. Jak zmieniać się może wynik sprzedaży każdego z wyrobów W₁ oraz W₂, by jednocześnie

rozwiązanie nie ulegało zmianie?

2. Czy i jak rozwiązanie optymalne ulegnie zmianie, jeżeli zapotrzebowanie dzienne na wyrób W₁

zmieni się o ∆W₁ a w stosunku do wyrobu W₂ nastąpi zmiana dziennego zapotrzebowania o

∆W₂,

3. Zmaleje efektywny fundusz godzin pracy o λ,

4. Zmaleją dostawy materiału do produkcji o μ.

Po uwzględnieniu nowych założeń należy rozwiązać zagadnienie postaci:

Warunki brzegowe:

x₁ ≥ 1000 + ∆W₁, x₂ ≥ 2000 + ∆W_2,

Warunki wewnętrznej zgodności:

3x₁ +6x₂ ≤ 24.000 + λ,

18x₁ +6x₂ ≤ 45.000 + μ,

Funkcja celu: Z(x₁, x₂) = (18 +ε₁) x₁ + (12 + ε₂) x₂.

---