WYZNACZANIE MOMENTU BEZWŁADNOŚCI

I SPRAWDZENIE TWIERDZENIA STEINLERA

1. Cele ćwiczenia :

1. Stwierdzenie zależności okresu drgań wahadła od momentu bezwładności

2. Doświadczalne potwierdzenie twierdzenia Steinlera

3. Wyznaczenie momentu bezwładności ciał względem osi przechodzącej przez środek masy

2. Wstęp teoretyczny

1. Wahadło fizyczne -jest to ciało doskonale sztywne ,które pod wpływem własnego ciężaru waha się dookoła osi O nie przechodzącej przez środek masy ciała .

2. Ruch harmoniczny Ruchem drgającym nazywamy każdy ruch lub zmianę stanu ,którą cechuje powtarzalność wartości wielkości fizycznych w czasie ,określających ten ruch lub sta
   n. Ruch drgający nazywamy ruchem okresowym(periodycznym) ,jeśli wartość wielkości fizycznych zmieniające się podczas drgań powtarzają się w równych odstępach czasu. Najprostszy ruch drgający to ruch harmoniczny określony wzorem: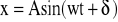
   . Wielkości charakteryzujące ten ruch to:

1. Amplituda (A)

2. Częstotliwość kołowa drgań (ω)

3. Okres drgań (T)

4. Faza drgań (ωt+б)

5. Faza początkowa (б₀)

1. Twierdzenie Steinlera Różnica momentów bezwładności ciała względem dwóch równoległych ,z których jedna przechodzi przez środek masy ciała równa jest iloczynowi masy (m) i kwadratu odległości (d) między osiami.

3. TARCZA

1. Pomiary wielkości TARCZY m= 416 [g] =0,416 [kg] Δm =1 [g] -0,001 [kg] 2d₁ =105,8 [mm] =0,1058 [m] d₁ =0,0529 [m] 2d₂ = 55,2 [mm] =0,0552 [m] d₂ =0,0276 [m] Δd₁= Δd₂=0,1 [mm] =0,0001 [m] Ilość drgań = 50

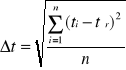
m -masa tarczy

Δm- odchyłka masy

Δt- błąd pomiaru czasu

d₁ ,d₂ -podwójna odległość od osi obrotu do środka masy tarczy

Δd₁ , Δd₂ -odchyłka podwójnej odległości od osi obrotu do środka masy tarczy

Rodzaj otworu		Czas dla 50 drgań (t) [s]			Δt [s]	Średnia (tśr.) [s]
Otwory zewnętrzny	Górny	32,0	30,0	30,2	0,3	30,5
		Dolny	30,3	30,3			30,3
	Otwory wewnętrzne	Górny	32,0	31,1			31,0	0,2	31,7
		Dolny	32,0	32,1			32,1

2. Moment bezwładności względem osi obrotu

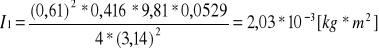
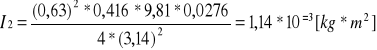
T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

d - podwójna odległość od osi obrotu do środka masy tarczy

I₁ - Moment bezwładności względem osi obrotu dla otworów zewnętrznych

I₂ - Moment bezwładności względem osi obrotu dla otworów wewnętrznych

3. Odchyłka od Moment bezwładności względem osi obrotu

ΔI₁ - Odchyłka od Moment bezwładności względem osi obrotu dla otworów zewnętrznych

ΔI₂ =Odchyłka od Moment bezwładności względem osi obrotu dla otworów wewnętrznych

T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

d - podwójna odległość od osi obrotu do środka masy tarczy

ΔT - Odchyłka okresu drgań

Δm - odchyłka masy

Δd - odchyłka podwójnej odległości od osi obrotu do środka masy tarczy

4. Moment bezwładności względem środka masy obliczany z twierdzenia Steinlera

I_0śr. =0,8905*10^-3

I₀₁- Moment bezwładności względem środka masy dla otworów zewnętrznych

I₀₂ - Moment bezwładności względem środka masy dla otworów wewnętrznych

I_0śr. - Średni Moment bezwładności względem środka masy

I - Moment bezwładności względem osi obrotu

m -masa tarczy

d - podwójna odległość od osi obrotu do środka masy tarczy

5. Odchyłki od Momentów bezwładności względem środka masy obliczana na podstawie twierdzenia Steinlera

ΔI₀₁ -Odchyłka od Moment bezwładności względem środka masy dla otworów zewnętrznych

ΔI₀₂ -Odchyłka od Moment bezwładności względem środka masy dla otworów wewnętrznych

m -masa tarczy

g -przyśpieszenie ziemskie

d - podwójna odległość od osi obrotu do środka masy tarczy

Δm - odchyłka masy

Δd - odchyłka podwójnej odległości od osi obrotu do środka masy tarczy

4. PIERŚCIEŃ

1. Pomiary wielkości PIERŚCIENIA m= 800 [g] =0,800 [kg] Δm =1 [g] = ,001 [kg] D =145 [mm] =0,145 [m] R=0,0725 [m]

d =115 [mm] =0,115 [m] DD r =0,0575 [m] ΔR= Δr=Δd=0,1 [mm] =0,0001 [m]

Ilość drgań = 100

Numer próby	1		2		3
Czas [s]	72		74		71
					wartość średnia [s]	tolerancja ± [s]
Numer próby	1	2		3
Okres [s]	0,72	0,74		0,71	0,723	0,001

2. Moment bezwładności względem osi obrotu

T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

I - Moment bezwładności względem osi obrotu

3. Odchyłka od Moment bezwładności względem osi obrotu

ΔI - Odchyłka od Moment bezwładności względem osi obrotu

T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

ΔT - Odchyłka okresu drgań

Δm - odchyłka masy

Δr - odchyłka odległości od osi obrotu do środka masy tarczy

4. Moment bezwładności względem środka masy obliczany z twierdzenia Steinlera

I₀- Moment bezwładności względem środka masy

I - Moment bezwładności względem osi obrotu

m -masa tarczy

d - odległość od osi obrotu do środka masy tarczy

5. Odchyłki od Momentów bezwładności względem środka masy obliczana na podstawie twierdzenia Steinlera

ΔI - Odchyłka od Moment bezwładności względem środka masy

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

Δm - odchyłka masy

Δr - odchyłka odległości od osi obrotu do środka masy tarczy

6. Moment bezwładności względem środka masy obliczany według tablicowego wzoru

I₀- Moment bezwładności względem środka masy

R -promień zewnętrzny pierścienia

r -promień wewnętrzny pierścienia

1. Odchyłka Momentu bezwładności względem środka masy obliczanego według tablicowego wzoru

5. WALEC

1. Pomiary wielkości WALCA

m= 800 [g] =0,800 [kg] Δm =1 [g] = ,001 [kg] DD D =145 [mm] =0,145 [m] R=0,0725 [m]DDDDDDDD

d =115 [mm] =0,115 [m] =2d r =0,0575 [m]

DDDDDDDDDDDDDDDDDDΔR= Δr=Δd=0,1 [mm] =0,0001 [m]

Ilość drgań = 100

Numer próby	1		2		3
Czas [s]	69		69		69
					wartość średnia [s]	tolerancja ± [s]
Numer próby	1	2		3
Okres [s]	0,69	0,69		0,69	0,690	0,001

1. Moment bezwładności względem osi obrotu

T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

I - Moment bezwładności względem osi obrotu

2. Odchyłka od Moment bezwładności względem osi obrotu

ΔI - Odchyłka od Moment bezwładności względem osi obrotu

T -okres drgań

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

ΔT - Odchyłka okresu drgań

Δm - odchyłka masy

Δr - odchyłka odległości od osi obrotu do środka masy tarczy

3. Moment bezwładności względem środka masy obliczany z twierdzenia Steinlera

I₀- Moment bezwładności względem środka masy

I - Moment bezwładności względem osi obrotu

m -masa tarczy

d - odległość od osi obrotu do środka masy tarczy

4. Odchyłki od Momentów bezwładności względem środka masy obliczana na podstawie twierdzenia Steinlera

ΔI - Odchyłka od Moment bezwładności względem środka masy

m -masa tarczy

g -przyśpieszenie ziemskie

r - odległość od osi obrotu do środka masy tarczy

Δm - odchyłka masy

Δr - odchyłka odległości od osi obrotu do środka masy tarczy

5. Moment bezwładności względem środka masy obliczany według tablicowego wzoru

I₀- Moment bezwładności względem środka masy

R -promień zewnętrzny pierścienia

r -promień wewnętrzny pierścienia

10. Odchyłka Momentu bezwładności względem środka masy obliczanego według tablicowego wzoru

6. Ocena błędów.

Porównując wartości momentów bezwładności względem środka ciężkości zauważamy, że wyniki nieco się różnią. Prawdopodobnie został popełniony błąd podczas mierzenia czasu wahnięć tego obiektu. Aby go uniknąć trzeba było wykonać więcej niż 100 wahnięć, co dałoby pewność, że nie popełniliśmy błędu podczas tego pomiaru lub też pomiar wielokrotnie powtórzyć i uśrednić wyniki pomiarów.

7. Wnioski.

1. Błąd ΔT ma największy wpływ na błąd wyniku momentu bezwładności ze względu na to, że T występuje we wzorze w drugiej potędze.

2. Obliczone wartości I₀ różnią się nieznacznie od siebie, co potwierdza prawdziwość twierdzenia Steinlera.

3. Błędy przy pomiarach czasu drgań spowodowane były głównie błędami przyrządu pomiarowego (stopera). Nie bez znaczenia pozostaje niedokładność odczytu suwmiarki przy pomiarze odległości oraz błąd wagi przy odczycie masy.

4

---