Ekonomia matematyczna - egzamin pytania poprawione

Pytanie 1.

Podać definicję towaru i opisać założenia go dotyczące.

Towar- jest to dobro lub usługa (rzecz lub czynność użyteczna) zaspokajające czyjąś

indywidualną potrzebę wyrażoną przez popyt na ten towar.

Założenia dotyczące towaru:

a). towary różnią się

- cechami fizycznymi

- miejscem i czasem ich dostępności

b). każdy towar ma określoną jednostkę np. szt,kg,litry,cm³

c). towary są nieskończenie podzielne (przyjmuje się, że ustalona jednostka każdego towaru

jest na tyle duża, że każda liczba rzeczywista określająca liczbę jednostek towaru ma sens,

np. można podzielić 1 kg mąki ale 1 szt samochodu nie ale 10 samochodów : ½ to 5

samochodów

d). ilość każdego towaru może być liczbą rzeczywistą dodatnią lub ujemną bądź zerem.

Np.

- wejście : to towar zużywany w procesie produkcji lub konsumpcji

- wyjście : to towar, który jest wynikiem procesu produkcji lub konsumpcji, jest

Udostępniany

Producenci mają wejścia(środki produkcji, nakłady, czynniki, surowce, praca) ujemne

a wyjścia (wyroby gotowe) dodatnie. Konsumenci natomiast odwrotnie.

Pytanie 2.

Zdefiniować przestrzeń wektorową
oraz zinterpretować ją jako przestrzeń

towarów.

Definicja:

Niech l € {1,2,…..}

={(v_1, v_2,v_3……..v_l) : v_1,v_2,v_3….v_l € R} - tj. zbiór ciągów liczb rzeczywistych o długości l

W zbiorze
określa się działania:

Jeżeli v = ( v_1…….v_l ) €

Jeżeli z = ( z_1,z_2…….z_l) €

Jeżeli λ € R

Wtedy

v + z = ( v₁ + z_{1, ……}v_l + z_l )

λ x v = ( λ * v₁, λ * v₂……λ * v_i )

Zbiór
z tak zdefiniowanymi działaniami nazywamy l- wymiarową, rzeczywistą przestrzenią wektorową, a jej elementy ( czyli te ciągi) nazywamy wektorami.

Interpretacja przestrzeni wektorowej jako przestrzeni towarów:

1. l oznacza liczbę towarów

2. wektor v €
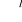
   traktujemy jako plan działania producenta lub konsumenta lub koszyk towarów gdzie k-ta współrzędna wektora v , czyli liczba v_k (k € {1,2,…..l})oznacza liczbę jednostek k-tego towaru w koszyku v , lub planowaną i przeprowadzoną wielkość produkcji lub konsumpcji

3. każdemu towarowi przypisana jest cała oś liczbowa, czyli każdy towar ma określone miejsce

4. wektor v z przestrzeni
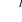
   v €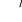
   jest wektorem typu wejście-wyjście.

Pytanie 3.

Zdefiniować przestrzeń wektorową
oraz zinterpretować ją jako przestrzeń cen.

Definicja przestrzeni:

Niech l € {1,2,…..}

={(v_1, v_2,v_3……..v_l) : v_1,v_2,v_3….v_l Є R} - tj. zbiór ciągów liczb rzeczywistych o długości l

W zbiorze
określa się działania:

Jeżeli v = ( v_1…….v_l ) Є

Jeżeli z = ( z_1,z_2…….z_l) Є

Jeżeli λ Є R

Wtedy

v + z = ( v₁ + z_{1, ……}v_l + z_l)

λ x v = ( λ * v₁, λ * v₂……λ * v_l )

Zbiór
z tak zdefiniowanymi działaniami nazywamy l- wymiarową, rzeczywistą przestrzenią wektorową, a jej elementy ( czyli te ciągi) nazywamy wektorami.

Interpretacja przestrzeni wektorowej jako przestrzeń cen:

Def: Ceną k-tego towaru p_k(k Є {1,2,…,l}) nazywamy liczbę rzeczywistą przypisaną jednej jednostce tego towaru, która pozwala na wartościowanie dóbr i usług.

Interpretacja:

1. p_k >0 cena dobra rzadkiego

2. p_k =0 cena dobra wolnego

3. p_k <0 cena dobra niechcianego (szkodliwego)

Def: Ceną ( wartością) koszyka υ=(v_1…v_l) Є
względem wektora (systemu) cen p=(p₁*p_2….* p_l) Є
nazywamy liczbę:

p◦ v = p₁*v₁+p₂*v₂+…+p_l* v_l

Pytanie 4.

Podać definicję systemu produkcji oraz opisać występujące w definicji pojęcia.

Na system produkcji składa się działalność producenta. Każdy producent wybiera dla siebie możliwy plan działania, aby maksymalizować zysk.

Def: System produkcji nazywamy układ relacyjny p=(J,
,y, p, η, π)

gdzie:

• J zbiór liczb {1,2,…,n} skończony zbiór producentów (n Є {1,2,3,…,})

• 
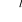
  przestrzeń towarów i cen

• y J З j →Y^j
  
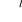
  jest korespondencją zbiorów produkcji

• p Є
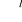
  wektor cen względem którego każdy producent osiąga max zysków na zbiorze

Y^j

• η : J З j → η^j (p)
  
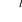
  korespondencja podaży η^j(p)- zbiór planów produkcji max zysk j-tego producenta (j ЄJ) na zbiorze Y^j względem systemu cen p

• π : J З j → π^j(p) Є R funkcja zysku maksymalnego, która każdemu producentowi przyporządkowuje jego zysk maksymalny na zbiorze Y^j względem systemu cen p.

Pytanie 5.

Opisać strukturę działania systemu produkcji

1. Wyznaczenie i opisanie zbioru T^j, czyli zbiorów tych systemów cen, dla których istnieje zysk maksymalny.

2. Wyznaczenie zbioru

ŋ^j (p) = { y^j*: y^j* maksymalizuje zysk przy danym systemie cen p na zbiorze Y^j* }

dla wektora p _Є T^j

3. Obliczenie wartości funkcji zysku maksymalnego

Π^j(p) = Π^j*(p) = p _° y^j*, gdzie y^j* _Є ŋ^j (p) dla każdego p _Є T^j

Uwaga!

Zysk maksymalny względem wektora cen p _Є ׀R^l istnieje na zbiorze y^j, jeżeli wektor p jest prostopadły do zbioru y^j w pewnym punkcie oraz zbiór y^j leży po drugiej stronie prostej stycznej do y^j w punkcie prostopadłości, niż wektor cen.

Ceny traktujemy jako dane. Jeśli cena p = (0,0), czyli dobra wolne, to dla każdego wektora y _Є Y^j , p _° y = 0 istnieje zysk maksymalny, zatem dla p = (0,0) _Є T^j zawsze istnieje zysk maksymalny. Stąd dla każdego j Є J : T^j ≠ ø

Pytanie 6.

Podać definicję i interpretację ekonomiczną wskazanych własności zbiorów produkcji. Podać przykład zbioru (narysować) w przestrzeni R² , który spełnia i takiego, który nie spełnia danej własności.

1.Domkniętość

Def.: Y i Y^j są domknięte granica każdego ciągu planów produkcji na leży do zbioru.

Interpretacja: Jeżeli wiadomo, że wektory leżące dowolnie blisko pewnego planu (wektora) y są technologicznie możliwe, to y jest technologicznie możliwy, tzn. (y _Є Y lub Y^j)

2 2

1 1

TAK(spełnia) NIE

2.Możliwość zaniechania produkcji

Def.: 0 _Є Y, 0=(0,…0) _Є R² (wektor zerowy)

Interpretacja: Możliwy z punktu widzenia dostępnych technologii jest plan produkcji, w którym wszystkie wejścia i wyjścia są równe zero.(Można nic nie robić).

2 2

1 1

TAK NIE

(ma możliwość zaniechania produkcji) (nie ma możliwości zaniechania produkcji)

3.Niemożliwość produkcji wolnej

Def.: Y∩ R²₊ = Ø lub Y∩ R²₊ = {0 }

Interpretacja: Nie można produkować z niczego. Każdy plan produkcji powinien zawierać wejścia. (Nie powinien zawierać elementów z I ćw.).

I ćw. I ćw.

TAK TAK

I ćw.

NIE

4.Nieodwracalność procesu produkcji

Def.: Y∩ (-Y) = Ø lub Y∩ (-Y) = {0 }

Interpretacja: Produkcji nie da się odwrócić. Jeżeli możliwy do realizacji jest pewien plan produkcji, w którym nie wszystkie wejścia i wyjścia są równe zero , to plan przeciwny nie jest możliwy do realizacji.

-Y

-Y

Y

-Y

Y=[-1,2] x[-2,3]

Y Y -Y=[-2,1] [-3,2]

Y∩ (-Y) = {0 } Y∩ (-Y) = Ø NIE

TAK TAK Y∩ (-Y) ≠Ø lub Y∩ (-Y)

Produkcja nie jest odwracalna zawiera więcej elementów niż wektor zerowy

5.Addytywność (dodawanie)

Def.: Y+Y
Y

Intrpretacja: Każde dwa plany możliwe do realizacji można zrealizować wspólnie ( z punktu widzenia dostępnych technologii).

Y₂

y₁ Y+Y=Y
Y

Y TAK

Dla każdego y¹, y² _Є Y, ich suma algebraiczna y¹+ y² _Є Y, stąd Y+Y
Y

TAK

Y

Y Y=[-2,3] x[-1,1]

Y+ Y=[-4,6] x[-2,2]

Y+Y
Y

Y+Y

NIE (nie ma właściwości addytywności)

6.Swobodny dostęp do dóbr

Def.: -R^l₊
Y (cała III ćwiartka powinna zawierać się w zbiorze Y)

Interpretacja: Wejścia procesu produkcyjnego nie są niczym ograniczone.

L=2 (płaszczyzna)

TAK NIE

7.Korzyści skali, które są związane ze zmianą intensywności procesu produkcji .

Trzy typy korzyści skali:

• niemalejące

Def.: Dla każdego t>1, y _Є Y wektor t ^.y _Є Y
każdy wektor ze zbioru Y można dowolnie wydłużyć w tym zbiorze.

Interpretacja: intensywność przeprowadzenia każdego planu produkcji może być dowolnie zwiększona.

TAK NIE

• nierosnące

Def.: Dla każdego t _Є [0,1], y _Є Y wektor t ^.y _Є Y
każdy wektor ze zbioru Y można dowolnie zmniejszyć w tym zbiorze.

Interpretacja: intensywność przeprowadzenia każdego planu produkcji może być dowolnie zmniejszona.

O,1 ^.y
Y

TAK NIE

• stałe

Def.: Dla każdego t≥0, y _Є Y wektor t ^.y _Є Y
każdy wektor ze zbioru Y można dowolnie wydłużyć lub skrócić w tym zbiorze.

Interpretacja: intensywność przeprowadzenia każdego planu produkcji może być dowolnie zwiększona lub zmniejszona.

TAK NIE

8.Wypukłość

Def.: Y jest wypukły dla każdych dwóch planów y¹, y² _Є Y ich plan przeciętny (średnioważony) ỹ należy do Y, gdzie: ỹ = t ^.y¹ + (1-t) ^.y² dla t _Є [0,1]

Interpretacja: Każdy plan średnioważony (przeciętny) planów możliwych do realizacji jest możliwy do realizacji.

ỹ
Y

NIE

TAK

Pytanie 12.

Zdefiniować ekonomię Debreu z własnością prywatną.

Def. Ekonomią Debreu z własnością prywatną nazywamy układ relacyjny

Ep= (K, P ω, Ө)

gdzie:

• P- system produkcji +

• ω (omega) ჎
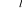
  -- całkowity zasób ekonomii

ωⁱ - zasób i- tego konsumenta, ω= ω¹+…+ ω^m - jest własnością prywatną

• Ө (teta) Ө I x J > (i,j) Өij ჎ ,  funkcja udziału

Өij -udział i-tego konsumenta w zyskach j- tego producenta

Dla każdego j ჎ J, Ө_1j + Ө_2j +......+ Ө_nj =1 Σⁿ_i=1 Өij = 1

Zysk j-tego producenta został rozdzielony pomiędzy konsumentów, zgodnie z funkcją Ө. Producent nic sobie nie zostawia , chyba że jest również konsumentem .

• K - system konsumpcji w którym majątek każdego i- tego konsumenta liczymy według wzoru .

wⁱ = p ° ωⁱ + Өi₁ x Π ^1*_(p) + Өi₂ x Π ^2*_(p)+ .......+ Өi_n x Π ^n*_(p)= p ° ωⁱ + Σⁿ_j=1 Өij x Π ^j*

i- konsument

j- producent

Ekonomia z własnością prywatną jest takim połączeniem systemów produkcji i konsumpcji

w którym konsumenci są właścicielami całkowitych zasobów ekonomii oraz uczestniczą

w zyskach producentów.

Pytanie 13.

Podać definicję stanu równowagi w modelu ekonomii z własnością prywatną.

Stanem ogólnej równowagi konkurencyjnej Walrasa w ekonomii E_p Debreu z własnością prywatną nazywamy ciąg:

(x^1*, x^2*, …x^m*, y^1*, y^2*, …y^m*, p ) _Є R^l(m+n+1)

m n 1

gdzie:

1. dla każdego i _Є I, x^i* maksymalizuje użyteczność i-tego konsumenta na zbiorze
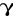
   (p,wⁱ) względem cen p^* _Є p, p=p* _Є R^l

2. dla każdego i-tego producenta (j _Є J), y^j* maksymalizuje zysk na zbiorze Y^j dla p = p^*

3. zachodzi warunek równowagi x^* - y^* = ω

Wektorem cen p^* nazywamy wektor cen równowagi

Jest to taka sytuacja, w której żaden podmiot ekonomiczny nie ma motywacji do zmiany swojego planu działania.

Pytanie 14.

Opisać zasadę działania ekonomii z własnością prywatną.

Dany jest wektor cen p ∈ R^l .

Etap1.

Każdy j-ty producent (j ∈ J) maksymalizuje swój zysk na zbiorze produkcji Y^j.

Niech Y^j* będzie planem produkcji maksymalizującym zysk, to znaczy y ^j* jest korespondencją podaży y ^j* ∈ η ^j(p), wówczas zysk max. j-tego producenta względem danego „p” liczymy ze wzoru i wynosi on:

Π ^j*(p) = p ° y ^j*

Jest on rozdzielony względem funkcji Ө pomiędzy konsumentów.

Өij x Π ^j*(p) - ta część zysku j-tego producenta, którą otrzymuje i-ty konsument.

(Na poprawionym opracowaniu od Lipiety etap pierwszy został oddzielony od II i III , z adnotacją,że zasada zawiera się tylko w pierwszym, ale zostawiłam resztę do waszego uznania,choć osobiście uważam ,że lepiej mniej niż więcej mieć do nauki.

Etap2.

Wyznaczamy majątek każdego i-tego konsumenta zgodnie z przepisem:

n

wⁱ = p ° ωⁱ + Σ Өij x Π ^j*(p)

j=1

Wyznaczamy elementy x ^i*∈ ζ ⁱ (p, wⁱ ) dla każdego i-tego konsumenta na zbiorze jego ograniczeń budżetowych:

γⁱ (p,wⁱ) = { x ∈ X ⁱ : p ° x < wⁱ }

Etap3.

Niech x^* = x ^1* + x ^2* +…….x ^n* będzie wektorem konsumpcji całkowitej oraz y ^* = y ^1* + y ^2* + ……y ^n* będzie wektorem produkcji całkowitej, takiej że :

x ^i* ∈ ζⁱ (p, wⁱ ) oraz y ^j*∈ η ^j(p), i ∈  , j ∈ J , jeżeli

zachodzi warunek : x^* - y^* = ω

to ekonomia Ep jest w stanie równowagi dla ceny równowagi : p^* = p

Wtedy p^* = p jest wektorem cen równowagi.

13

---