zad.1 Zbadać zbieżność szeregu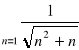

zad.1 Zbadać zbieżność szeregu

zad.2 Wyznaczyć ekstrema lokalne funkcji
,

zad.2 Wyznaczyć ekstrema lokalne funkcji

zad.3 Obliczyć przybliżoną wartość wyrażenia
zastępując przyrost odpowiednio wybranej funkcji przez jej różniczkę zupełną.

zad.3 Obliczyć przybliżoną wartość wyrażenia
zastępując przyrost odpowiednio wybranej funkcji przez jej różniczkę zupełną.

zad.4 Rozwinąć w szereg Maclaurina funkcję
.

Podać przedział zbieżności szeregu.

Wyznaczyć
- wartość dziewiątej pochodnej funkcji f w punkcie 0.

zad.4 Rozwinąć w szereg Maclaurina funkcję
.

Podać przedział zbieżności szeregu.

Wyznaczyć
- wartość dziewiątej pochodnej funkcji f w punkcie 0.

zad.5 Funkcja
jest określona wzorem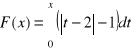
dla
.

a) Wyznaczyć przedziały, w których funkcja F jest rosnąca.

b) Wyznaczyć punkty z przedziału
, w których funkcja F osiąga ekstrema lokalne, określić ich rodzaj (maksimum, minimum). Nie obliczać wartości ekstremalnych.

c) Wyznaczyć punkty z przedziału
, w których funkcja F nie ma pochodnej.

Odpowiedzi uzasadnić.

zad.5 Funkcja
jest określona wzorem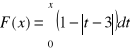
dla
.

a) Wyznaczyć przedziały, w których funkcja F jest malejąca.

b) Wyznaczyć punkty z przedziału
, w których funkcja F osiąga ekstrema lokalne, określić ich rodzaj (maksimum, minimum). Nie obliczać wartości ekstremalnych.

c) Wyznaczyć punkty z przedziału
, w których funkcja F nie ma pochodnej.

Odpowiedzi uzasadnić.

1

---