Teoria Analiza Matematyczna

1. Kresy zbiorów, definicja.

• kresem górnym (zbioru niepustego i ograniczonego) nazywamy najmniejsze ograniczenie górne.

Niepusty podzbiór X zawarty w prostej nazywamy ograniczonym z góry <=>

• kresem dolnym (zbioru niepustego i ograniczonego) nazywamy największe ograniczenie dolne.

Niepusty podzbiór X zawarty w prostej nazywamy ograniczonym z dołu<=>

2. Twierdzenie: a=sup x, b=inf x

a= sup x <=> 1. a ogranicza X z góry

2.

b= inf x <=> 1. b ogranicza X z dołu

2.

3. Granica ciągu

def. Liczbę a
R nazywamy granicą ciągu a_n <=>

Pokazać, że lim a_n =
, a_n =

Załóżmy, że
=

Czy istnieje
taka że
dla n>
?

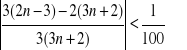
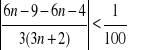
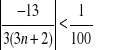
1300<9n+6

1294<9n

n>154=

odp. A zatem dla n
155 wyrazy ciągu a_n
(
;
)

4. Twierdzenie o sumach, iloczynach itp. granic.

Dowód:
a_n =a;
b_n =b

Czy (a_n + b_n )= a_n + b_n ?

To znaczy czy dla dowolnie ustalonego
>0 istnieje taka liczba
, że dla n>

Ustalamy
>0.

Ponieważ a_n
a, więc istnieje
, że dla n>

Ponieważ b_n
b, więc istnieje
, że dla n>

Przyjmijmy, że
=max (
,
) Wówczas dla n>

=

5. Tw. Każdy ciąg zbieżny jest ograniczony.

Przyjmujemy
=1. Ponieważ a_n
a (jest zbieżny) więc istnieje n, że dla n>n₁

Przyjmujemy m=min

M=max

Wówczas m
a_n
M dla każdego n
N

6. Twierdzenie o 3 ciągach.

Dowód: Dane są ciągi a_n
b_n
c_n . Jeśli
a_n =
c_n to także b_n jest zbieżne do tej granicy.

Oznaczamy
a_n =
c_n = g. Niech
>0

Z tego, że a_n
g istnieje n, że dla n>n” g -
< a_n <g +

Z tego, że c_n
g istnieje n, że dla n>n” g -
< c_n <g +

A zatem dla n>max(n';n”) g -

b_n
g +

7. Tw. Bolano-Weierstrassa
Każdy ciąg ograniczony posiada podciąg zbieżny:

Dowód: Wartości ciągu ograniczonego (a_n ) są zawarte w przedziale [m,M]. Podzielimy go na 2 równe części. W co najmniej jednej z nich znajduje się nieskończenie wiele wyrazów ciągu (a_n ). Oznaczamy tą część [m₁,M₁] i niech (a_mn ) oznacza podciąg nieskończony zawarty w [m₁,M₁]. Przyjmujemy b₁ =a_n1. Następnie dzielimy przedział [m₂,M₂] na dwie równe części w jednej z nich [m₂,M₂] znajduje się podciąg
i przyjmujemy b₂ =

Postępując tak dalej znajdujemy ciągi m_k
b_k
M_k gdzie b_k jest podciągiem (a_n ) zaś (m_k) i (M_k) są monotoniczne i mają wspólną granice. A zatem z Tw. o trzech ciągach także podciąg b_n jest zbieżny do tej granicy.

Tw: Ciąg monotoniczny i ograniczony jest zbieżny.

Dowód: Niech ciąg (a_n ) będzie rosnący. Pokażemy że jest on zbieżny do liczby

a=sup {a_n : n
N}.

Ustalmy
>0. Pokażemy że w odc. (a-
,a] znajdują się prawie wszystkie wyrazy ciągu a_n

1. a_n
a
sup{a_n}

2. Z def. sup{a_n} istnieje wyraz
>a-
. A zatem dla n>n_o

a-
<
< a_n
a czyli a_n
(a-
,a]

8. Podstawowe granice:

• 
  
  

Niech a
1. Oznaczamy
. Pokażemy, że

0. Otóż

0 a więc a= (1+
)ⁿ =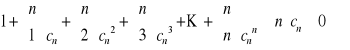

[
]
0 z tw. o 3 ciągach

• 
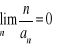
  a>0

Niech a=1+c gdzie c>0. Wówczas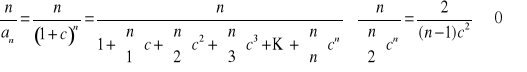

• 
  

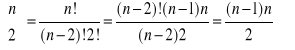
Dowód: dla a=2

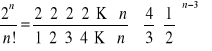
0<
<

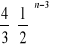
0

• 
  

Niech n=2k lub 2k +1. Wówczas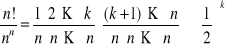

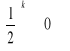
9. Liczba e. Dowód zbieżności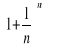
. interpretacja.

Rozpatrzmy ciąg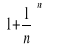
. Pokażemy, że jest on ograniczony

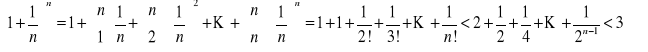
Z tej interpretacji wynika, że ciąg jest rosnący a dalej zbieżny. Tą granice oznaczamy e
2,71828...

Ex. Wpł. dzbanku 1zł na okres roku z oprocentowaniem 100%. Po roku będziemy mieli 1+1=2zł. Gdyby odsetki dopisywano po
roku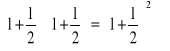
. Gdyby po 4 miesiącach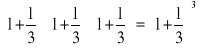
. Gdyby po n miesiącach to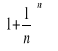
. A zatem ciąg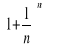
jest rosnący.

II. Przestrzenie metryczne.

10. Przestrzeń metryczna. Def i Ex.

Def.

1. d (x,y)
0 odległ
0

2. d (x, y) =0
x=y

3. d (x, y) = d (y, x) symetryczne

4. d (x, y) + d (y, z)
d (x, z)- nierówność trójkąta

11. Zbieżność ciągu w przestrzeni metrycznej.

Def. Ciąg punktów
nazywamy zbieżnym do punktu
( jako zwykły ciąg na prostej).

Uwaga: Definicja ta jest zgodna ze zwykłą zbieżnością gdy X=R.

12. Tw. zbieżność w Rⁿ = zbieżność po współrzędnych. Dowód.

(x_n, y_n)
(x_0, y₀) tzn. x_n
x₀ ; y_n
y₀

Dowód: Uwaga dla liczb a, b
0 zachodzi nierówność

A zatem:

Dla ciągu punktów z_n =( x_n, y_n) i z_o =( x_o, y_o)

Jeśli np.
lub
to
, dlatego reszta metryk też dąży do zera.

Ex. z_n (1;
)

13. Zbiór otwarty, domknięty. Definicja.

Zbiór domknięty: Podzbiór
nazywamy domkniętym
granica każdego ciągu punktów x_i
D zbieżnego w X należy do D.

Podzbiór przestrzeni metrycznej
nazywamy otwartym

Ex. X=R² (metoda Euklid.) U={(x,y): y>0} jest otwarty, bo jeśli K(( x_o, y_o);
)
U.

14 TW Zbiór
jest otwarty
jest domknięty .

Na prostej zbiór (a,b) jest zbiorem otwartym
zbiorem domkniętym.

15. TW. Suma dwóch zbiorów domkniętych jest zbiorem domkniętym.

zbiory domknięte

domknięte

Mamy pokazać że
jest domknięty tzn. [niech
Wówczas nieskończenie wiele wyrazów ciągu należy do A lub B . Przypuśćmy że do „A”. A więc ustalamy podciąg
. Wówczas
(jako podciąg) a zatem z domkniętości A,
. A więc
.

16. TW. Część wspólna skończonej ilości zbiorów domkniętych jest zbiorem domkniętym.

Niech zbiór
będzie domkniętych. Czy
też jest zbiorem domkniętym. Mamy pokazać że
jest domknięty U_1,…,U_n są domknięte czyli niech
. Wówczas jako że x_n należy do każdego U_i to znaczy że
. A zatem część wspólna nieskończenie wielu zbiorów domkniętych jest zbiorem domkniętych.

17. TW: Suma dowolnej ilości zbiorów otwartych jest zbiorem otwartym.

Niech zbiór
będzie otwarte. Czy
U_i też jest otwarte. Niech
U_i . To znaczy istnieje
takie że
. Ponieważ U_i0 jest otwarty więc istnieje r₀>b takie że K(x₀,r₀)
. A więc K(x₀,r₀)
.

19. TW. Odwzorowania ciągłe. Def. Heinego Couchy'ego i ich równoważności.

Dane są przestrzenie metryczne (X, d_x), (Y, d_y) oraz odwzorowanie f:
. Małe zmiany argumentów powodują małe zmiany funkcji.

(Heine)Mówimy że funkcja f jest ciągła w punkcje x₀
dla każdego ciągu punktów x_n przestrzeni x zachodzi implikacja.

Funkcja przeprowadza ciągi zbieżne do x₀ na ciągi zbieżne do f(x₀)

(couchy) Mówimy że funkcja f jest ciągła w punkcie

i f(x₀)<

20. TW. Suma ,iloczyn, iloraz funkcji ciągłych f, g :
są ciągłe.

Dowód: korzystamy z def. Heinego. Mamy pokazać że dla każdego ciągu
. Ciąg wartości f(x_n)+g(x_n) dąży do (f(x₀)+g(x₀)).

Jest tak bo z założenia ciągłości funkcji
a z założenia f(x_n)
. A więc

bo granica sumy = sumie granic.

Podobnie dla iloczynu i ilorazu.

21. Przestrzeń zwarta: definicja, przykłady

Przestrzeń metryczną nazywamy zwartą każdy ciąg punktów tej przestrzeni posiada podciąg zbieżny.

Ex.: odcinek domknięty [a,b]
R(tw. Bolano-Weistra.), prostokąt domknięty [a₁,b₁] [a₂,b₂] ze zwartości poszczególnych odcinków [a₁,b₁] [a₂,b₂] wynika zbieżność odpowiednich !!!podciągów!!! x_nk --> x₀[a₁b₁] etc.; kostka domknięta; każda przestrzeń skończona jest zwarta(metryczna); przestrzeń dyskretna jest zwarta gdy jest skończona.

22. Każda przestrzeń metryczna skończona jest zwarta

Bo każdy ciąg x_n przyjmuje jedna z wartości nieskończenie wiele razy. A to daje podciąg stały.

23. TW. Podzbiór A
Rⁿ jest zwarty jest domknięty i ograniczony

Dowód: Jeśli A
Rⁿ jest domknięty i ograniczony to jest zwarty w pewnej kuli K(0;R). Z kolei kula ta jest zwarta w pewnej kostce domkniętej K(0;R)
[-R,R]x…x[-R,R], a kostka jest zbiorem zwartym.

Czy A jako podzbiór zbioru zwartego jest zwarty => Niech A
Rⁿ będzie zwarty. Jako zwarty jest ograniczony. Pozostaje pokazać że A jest domkniety. Niech (a_n) będzie ciagiem punktów i A zbieżny x₀
Rⁿ . Czy x₀
A???

Ze zwartości ciągu (a_n) posiada podciąg zbieżny do punktu a₀<A. A podciąg ten jest zbieżny do x₀. A więc x₀ = a₀
A.

24. TW. Weierstrassa: F-cja f:X
R (X zwarta) jest ograniczona i osiąga swoje kresy.

Dowód:

1. Wobec lematu (obraz ciągły przestrzeni jest przestrzenią zwartą) f(x)
   R jest zbiorem zwartym. A więc jest ograniczony czyli istnieja liczby m,M dla których f(x)
   [m,M]

2. Skoro f(x)
   R jest zwarty to jest i domknięty. A zatem zawiera swoje kresy czyli istnieją punkty X _- , X₊ dla których f(X₊) = sup f(x), f(X _- )= inf f(x)

25. Przestrzeń spójna: definicja przykłady

Przestrzeń metryczna nazywamy spójną istnieją zbiory niepuste i otwarte U,V
X takie, że nie da się przedstawić (nie zachodzą „relacje”) U
V = X U
V =

Ex.: R jest spójne, C jest spójne. Każdy przedział liczbowy jest spójny.

26. Łukowa spójność. Każda przestrzeń łukowo spójna jest spójna.

Funkcja f:X
Y jest ciągła przeciwobrazem zbioru otwartego jest zbiór otwarty.

Nie wprost: Zakładamy, że przestrzeń X jest łukowo spójna ale nie jest spójna. Tzn. X=U
V gdzie U i V są otwarte, rozłączne i niepuste. Ustalamy punkty a
U, b
V. Z założenia łukowej spójności istnieje droga U:[0,1]
X taka, że w(0)=a i w(1)=b. Zauważmy, ze [0,1]=w^-1(X)=w^-1U
w^-1V. Ponadto zbiory w^-1U, w^-1V są rozłączne, otwarte, niepuste. A to dowodzi, że odcinek [a,b] jest niespójny. Sprzeczność.!!!

27. TW. Darboux. Każdy wielomian stopnia nieparzystego posiada pierwiastek rzeczywisty.

f(x)=a₀xⁿ+a₁x^n-1+…+a_n gdzie n-nieparzyste. Wówczas
f(x)=+
a₀>0.
f(x)=
, a zatem istnieją liczby T,t dla których f(T)>0 i f(t)<0. Stąd z własności Darboux istnieje x₀
(T,t) w którym f(x₀)=0.

RACHUNEK RÓŻNICZKOWY I CAŁKOWY

28. Iloraz różnicowy i jego interpretacja. Definicja pochodnej (styczna, prędkość)

Ilorazem różnicowym nazywamy wyrażenie
. Liczbę h nazywamy przyrostem argumentu, inne oznaczenia
. Zaś
przyrostem funkcji. Wówczas iloraz różnicowy to
.

Interpretacja geometryczna

tg kata nachylenia siecznej z osią OX.

Interpretacja fizyczna
. S(t₀) oznacz położenie ciała w chwili t. Wówczas
oznacza średnią prędkość w czasie [t₀,t₀+h].

Pochodna funkcji f w punkcie x₀ nazywamy granicę ilorazu różnicowego
o ile istnieje. Oznaczamy f^'(x₀)=
(x₀). Interpretacja pochodnej - prędkość chwilowa.

29. TW. Fermata (ekstremum
f^'(x)=0. )

Dowód: Załóżmy, że f posiada w x₀ maksimum lokalne. Oznacza to, że f(x)
f(x₀) dla wszystkich x
(
) i pewnego
. A zatem dla
iloraz różnicowy
zas dla x<x₀ jest dodatni. A zatem granica o ile istnieje musi być 0.

30. TW.Rolle'a (o zerowaniu się pochodnej)

Warunek konieczny do istnienia ekstremum. Czy war. konieczny??

Jeśli f:[a,b]
R ma wszędzie pochodną oraz f(a)=f(b) to istnieje punkt c
(a,b) w którym f^'(c)=0. Dowód:

1. jeśli f jest stała to f'=0

2. jeśli f nie jest stała to dla pewnego x
   (a,b) zachodzi f(x)=f(a). Załóżmy f(x)>f(a). Wówczas z tw. Weierstrassa f osiąga swoje maksimum w punkcie c
   (a,b). A zatem z (tw. Fermata) f'(c)=0.

31. TW. Lagrange'a (dowód)

Jeśli f:[a,b]
R jest ciagła na [a,b] oraz posiada pochodna w (a,b) to wówczas istnieje c
(a,b) takie, że f(b)-f(a)=f'(c)(b-a).

Dowód:

Mamy znaleźć punkt c
(a,b) spełniający
czyli szukamy punktu w którym styczna jest równoległa do siecznej przechodzącej przez punkty (a,f(a)) oraz (b,f(b)). Określamy funkcje pomocniczą
. Funkcja spełnia założenia Rolle'a g(a)=g(b)=0. A zatem istnieje punkt c
(a,b) w którym g'(c)=0. A zatem 0=g'(c)=
skąd
.

32. Reguła de l'Hospitala

Jeśli funkcje f i g są określone w przedziale [a,b] oraz

1.

2.

3. istnieją skończone pochodne f'(a), g'(a) przy czym g'(a)
0 wówczas

33. Sumy całkowe Reimanna. Całka oznaczona.

Ustalamy podział odcinka [a;b] na części. W każdej wybieramy punkt
. Tworzymy sumę
. Sumę tą nazywamy sumą całkową Reimanna. Zależy ona od wybranego przedziału [a;b] i selekcji
. Suma ta daje łączne pole prostokątów opisanych na wykresie.

34. Interpretacja całki oznaczonej.

Geometryczna- pole pod wykresem funkcji

Fizyczna- Niech w każdym punkcie odcinka [a;b] działa F(x) skierowana wzdłuż prostej. Wówczas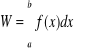

35. Zasadnicze twierdzenie rachunku różniczkowego i całkowego. Uzasadnić że funkcja górnej granicy całki jest funkcją pierwotną.

1.Niech
będzie całkowalna. Dla ustalonego
określamy
. Funkcję F(x) nazywamy funkcją górnej granicy całkowania.

2. Ustalamy
oraz h>0. Badamy iloraz różniczkowy . Z twierdzenia o wartości średniej dla całki istnieje
spełniające
. Wówczas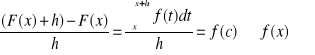
gdy

A to oznacza że

---