Nr ćwiczenia: 5	Data wykonania: 25.06.2012	Imię, Nazwisko: Bartosz Minta	PWSZ w Kaliszu 2011/2012	Kierunek: MBM niest. grupa lab. 1	Nr zespołu: 2
Temat ćwiczenia: Wyznaczanie przyspieszenia grawitacyjnego za pomocą wahadła balistycznego		Prowadzący: Dr. inż. Justyna Barańska	Przygotowanie:	Opracowanie:	Ocena ostateczna:

1. Część teoretyczna:

Wahadło - ciało zawieszone lub zamocowane ponad swoim środkiem ciężkości wykonujące w pionowej płaszczyźnie drgania pod wpływem siły grawitacji. W teorii mechaniki rozróżnia się dwa podstawowe rodzaje wahadeł:

- matematyczne,

- fizyczne.

Ważną cechą wahadła fizycznego i matematycznego jest stałość okresu drgań dla niewielkich wychyleń wahadła.

Wahadło matematyczne:

Punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego.

Ogólne równanie ruchu wahadła matematycznego:

Gdzie:

- l - długość nici,

- g - przyspieszenie ziemskie,

- m - masa ciała,

- θ - kąt wektora wodzącego ciała z pionem

- A - amplituda siły wymuszającej

- ω_D - częstość siły wymuszającej

- γ - współczynnik oporu ośrodka

Równanie to odpowiada równaniu drgań tłumionych o sile nieproporcjonalnej do wychylenia, czyli drgań nieharmonicznych. Równania tego nie da się rozwiązać analitycznie, nawet gdy A=0.

Dla małych wychyleń funkcję sinus można przybliżyć przez zastosowanie prawidłowości:

Stosując powyższe przybliżenie, pomijając opory oraz siłę wymuszającą równanie, otrzymuje postać:

Równanie, to odpowiada równaniu oscylatora harmonicznego o częstości:

Wahadło fizyczne:

Bryła sztywna mogąca wykonywać obroty dookoła poziomej osi przechodzącej ponad środkiem ciężkości tej bryły.

Wzór na okres drgań wahadła fizycznego dla małych wychyleń:

Przez analogię do wahadła matematycznego wzór ten zapisuje się jako:

Wprowadzając wielkość długość zredukowana wahadła l₀

gdzie:

- d - odległość od punktu zawieszenia do środka ciężkości,

- g - przyspieszenie ziemskie,

- I - moment bezwładności ciała względem osi obrotu,

- m - masa ciała.

Inne rodzaje wahadeł:

- wahadło torsyjne,

- wahadło rewersyjne,

- wahadło żyroskopowe,

- wahadło balistyczne,

- wahadło kolejowe,

- wahadło Oberbecka,

- wahadło zegarowe,

- wahadełko (wahadło radiestezyjne).

Szczególnym przykładem zastosowania właściwości wahadeł jest zegar wahadłowy.

Wzory użyte w ćwiczeniu:

Przyspieszenie grawitacyjne

Okres drgań wahadła

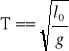
II. Spis przyrządów pomiarowych i wyniki pomiarów

Nazwa przyrządu	Dokładność pomiaru
Wahadło balistyczne	1°
		Zegar elektroniczny	0,001s
		Linijka	0,001m

Wartość mierzona	Jednostka	Pomiar 1	Pomiar 2	Pomiar 3	Wartość średnia
L1	[m]	0,160	0,160	0,160	0,160
ϕ0	[°]	0°
T0	[s]	0,811	0,812	0,811	0,8113
gdoświadcz.	m/s^2	9,6037	9,5800	9,6037	9,5958
ϕ1	[°]	5°
T1	[s]	0,814	0,814	0,814	0,8140
gdoświadcz.	m/s^2	9,5694	9,5694	9,5694	9,5694
ϕ2	[°]	10°
T2	[s]	0,82	0,82	0,82	0,8200
gdoświadcz.	m/s^2	9,5389	9,5389	9,5389	9,5389
ϕ3	[°]	15°
T3	[s]	0,8270	0,8270	0,8270	0,8270
gdoświadcz.	m/s^2	9,5615	9,5615	9,5615	9,5615
ϕ4	[°]	20°
T4	[s]	0,8380	0,8380	0,8380	0,8380
gdoświadcz.	m/s^2	9,5721	9,5721	9,5721	9,5721
ϕ5	[°]	25°
T5	[s]	0,8550	0,8540	0,8550	0,8547
gdoświadcz.	m/s^2	9,5339	9,5563	9,5339	9,5414
ϕ6	[°]	30°
T6	[s]	0,8750	0,8710	0,8720	0,8727
gdoświadcz.	m/s^2	9,5265	9,6142	9,5922	9,5775
Φ7	[°]	35°
T7	[s]	0,8950	0,8930	0,8960	0,8947
gdoświadcz.	m/s^2	9,6265	9,6697	9,6050	9,6337
Φ8	[°]	40°
T8	[s]	0,9320	0,9330	0,9310	0,9320
gdoświadcz.	m/s^2	9,4928	9,4725	9,5132	9,4928
Φ9	[°]	45°
T9	[s]	0,9530	0,9530	0,9540	0,9533
gdoświadcz.	m/s^2	9,8358	9,8358	9,8152	9,8289
Φ10	[°]	50°
T10	[s]	1,0060	1,0060	1,0040	1,0053
gdoświadcz.	m/s^2	9,7099	9,7099	9,7487	9,7228
Φ11	[°]	55°
T11	[s]	1,0530	1,0570	1,0540	1,0547
gdoświadcz.	m/s^2	9,9319	9,8569	9,9130	9,9005
Φ12	[°]	60°
T12	[s]	1,1280	1,1280	1,1280	1,1280
gdoświadcz.	m/s^2	9,9287	9,9287	9,9287	9,9287
Φ13	[°]	65°
T13	[s]	1,2200	1,2190	1,2160	1,2183
gdoświadcz.	m/s^2	10,0418	10,0583	10,1080	10,0693
Φ14	[°]	70°
T14	[s]	1,3370	1,3320	1,3360	1,3350
gdoświadcz.	m/s^2	10,3315	10,4093	10,3470	10,3625
Φ15	[°]	75°
T15	[s]	1,5280	1,5240	1,5240	1,5253
gdoświadcz.	m/s^2	10,4529	10,5078	10,5078	10,4895
Φ16	[°]	80°
T16	[s]	1,7820	1,7790	1,7810	1,7807
gdoświadcz.	m/s^2	11,4550	11,4936	11,4678	11,4721
Φ17	[°]	85°
T17	[s]	2,3010	2,3010	2,2980	2,3000
gdoświadcz.	m/s^2	13,6883	13,6883	13,7241	13,7002
gdoświadcz.średnia	m/s^2	10,0865
gobliczone	m/s^2	9,823

Wartość mierzona	Jednostka	Pomiar 1	Pomiar 2	Pomiar 3	Wartość średnia
L2	[m]	0,230	0,230	0,230	0,230
ϕ0	[°]	0°
T0	[s]	0,957	0,957	0,956	0,9567
gdoświadcz.	m/s^2	9,9143	9,9143	9,9351	9,9212
ϕ1	[°]	5°
T1	[s]	0,959	0,96	0,959	0,9593
gdoświadcz.	m/s^2	9,9107	9,8901	9,9107	9,9039
ϕ2	[°]	10°
T2	[s]	0,964	0,965	0,965	0,9647
gdoświadcz.	m/s^2	9,9216	9,9011	9,9011	9,9079
ϕ3	[°]	15°
T3	[s]	0,9740	0,9740	0,9740	0,9740
gdoświadcz.	m/s^2	9,9089	9,9089	9,9089	9,9089
ϕ4	[°]	20°
T4	[s]	0,9880	0,9880	0,9890	0,9883
gdoświadcz.	m/s^2	9,8989	9,8989	9,8789	9,8922
ϕ5	[°]	25°
T5	[s]	1,0070	1,0070	1,0080	1,0073
gdoświadcz.	m/s^2	9,8799	9,8799	9,8603	9,8734
ϕ6	[°]	30°
T6	[s]	1,0310	1,0300	1,0310	1,0307
gdoświadcz.	m/s^2	9,8637	9,8829	9,8637	9,8701
Φ7	[°]	35°
T7	[s]	1,0590	1,0610	1,0600	1,0600
gdoświadcz.	m/s^2	9,8840	9,8467	9,8653	9,8653
Φ8	[°]	40°
T8	[s]	1,0940	1,0930	1,0930	1,0933
gdoświadcz.	m/s^2	9,9037	9,9219	9,9219	9,9158
Φ9	[°]	45°
T9	[s]	1,1410	1,1390	1,1400	1,1400
gdoświadcz.	m/s^2	9,8635	9,8982	9,8808	9,8808
Φ10	[°]	50°
T10	[s]	1,1920	1,1900	1,1900	1,1907
gdoświadcz.	m/s^2	9,9419	9,9753	9,9753	9,9641
Φ11	[°]	55°
T11	[s]	1,2570	1,2580	1,2570	1,2573
gdoświadcz.	m/s^2	10,0190	10,0031	10,0190	10,0137
Φ12	[°]	60°
T12	[s]	1,3580	1,3560	1,3580	1,3573
gdoświadcz.	m/s^2	9,8473	9,8764	9,8473	9,8570
Φ13	[°]	65°
T13	[s]	1,4500	1,4480	1,4470	1,4483
gdoświadcz.	m/s^2	10,2189	10,2471	10,2613	10,2424
Φ14	[°]	70°
T14	[s]	1,6020	1,5980	1,5990	1,5997
gdoświadcz.	m/s^2	10,3445	10,3964	10,3834	10,3747
Φ15	[°]	75°
T15	[s]	1,8240	1,8230	1,8240	1,8237
gdoświadcz.	m/s^2	10,5449	10,5565	10,5449	10,5487
Φ16	[°]	80°
T16	[s]	2,1380	2,1320	2,1290	2,1330
gdoświadcz.	m/s^2	11,4394	11,5038	11,5363	11,4931
Φ17	[°]	85°
T17	[s]	3,0330	3,0230	3,0260	3,0273
gdoświadcz.	m/s^2	11,3252	11,4003	11,3777	11,3677
gdoświadcz.średnia	m/s^2	10,1556
gobliczone	m/s^2	9,823

Kąt odchylenia ϕ	gdoświadcz dla L1	Kąt odchylenia ϕ	gdoświadcz dla L2
[°]	m/s^2	[°]	m/s^2
0	9,60	0	9,92
5	9,53	5	9,87
10	9,39	10	9,76
15	9,24	15	9,57
20	8,99	20	9,30
25	8,65	25	8,95
30	8,29	30	8,55
35	7,89	35	8,08
40	7,27	40	7,60
45	6,95	45	6,99
50	6,25	50	6,40
55	5,68	55	5,74
60	4,96	60	4,93
65	4,26	65	4,33
70	3,54	70	3,55
75	2,71	75	2,73
80	1,99	80	2,00
85	1,19	85	0,99

1. Obliczenia

1. Obliczenia wartości średnich

- wartości średnie okresów drgań dla l₁

Pozostałe wartości w tabeli

- wartości średnie okresów drgań dla l₂

Pozostałe wartości w tabeli

2. Obliczenia g_doświadcz ze wzoru na okres drgań wahadła ( z uwzględnieniem kąta odchylenia od pionu ϕ)

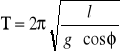
/²

/*g

/: T²

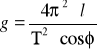
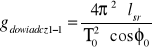
- dla l₁

- dla l₂

3. Obliczenia g

G - stała grawitacji

M - masa Ziemi,

R - promień Ziemi

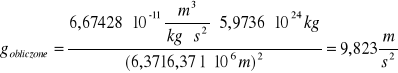
4. Obliczenia g_k księżyca

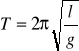
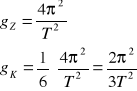
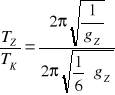
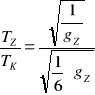
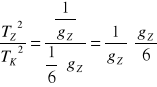
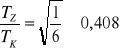
Dla l₁
:

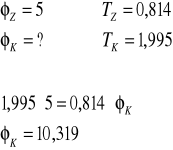
Dla l₂
:

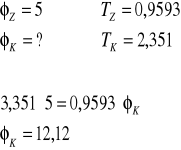
2. Rachunek błędów

∆T=0,001[s] - dokładność zegara elektronicznego

∆l=0,001[m] - dokładność odczytu linijki

- błąd l_1śr

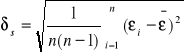
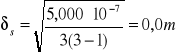
- błąd dla l₂ również wynosi 0

- błąd T dla l₁

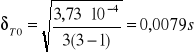
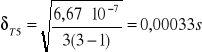
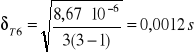
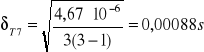
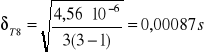
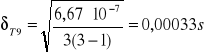
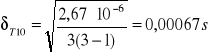
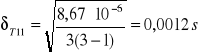
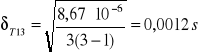
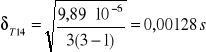
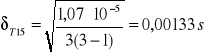
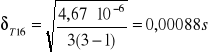
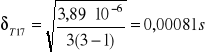
- błąd T dla l₂

,
,
,
,
,

,
,
,
,
,

,
,
,
,

,

-błąd g dla l₁

-błąd g dla l₂

3. Zestawienie wyników

4. Wykresy

- dla l₁=160mm

- dla l₂=230mm

V. Wnioski

Teoretycznie przyspieszenie grawitacyjne g na Ziemi wynosi 9,81
. Wyniki uzyskane w danym doświadczeniu bardzo odbiegają od tej wartości. Przyspieszenie ziemskie zależy głównie od odległości ciała od danego źródła pola magnetycznego. Na błąd pomiaru duży wpływ miała mała dokładność pomiaru długości z użyciem linijki (1mm) oraz w największym stopniu pomiar kąta odchylenia wahadła.

Załączone wykres odzwierciedla wartość składowej siły g w ruchu wahadła w zależności od jego odchylenia od pionu.

---